利用灰成分预测煤灰熔融温度的模型研究

胡洋，张晔，操岳峰

利用灰成分预测煤灰熔融温度的模型研究

胡洋，张晔，操岳峰

（安徽理工大学化学工程学院，安徽淮南232001）

以149种硅铝比在1.8～3.0之间、碱性组分质量分数小于30%的煤样的灰流动温度（FT）为基础，引入影响因子FI，通过最小二乘法进行拟合，建立了关联各煤灰氧化物成分的熔融温度预测模型，相关性系数达0.974 2，该模型预测值与实验结果有较好的一致性。

影响因子；最小二乘法；煤灰熔融温度；预测模型

气流床气化技术是大规模、高效清洁煤基燃气与合成气制备的首选技术，操作温度高达1 300～1 700℃，煤中矿物质转变成煤灰并经过高温过程形成灰渣[1]。为保证灰渣顺利排出，入炉煤的流动温度一般要低于气化炉操作温度50～100℃[2]。但实际生产中很少有煤种能够直接符合入炉煤条件，因此需要配煤或添加助熔剂以改变煤种的特性，为快速找到合适的配煤煤种或助熔剂，减少传统配煤过程中的盲目性从而提高工作效率，现对煤灰化学组成和煤灰熔融温度进行研究以期找到合适的煤灰熔融温度预测模型。

Vargas等通过多元回归方法研究了54种无烟煤灰的灰成分对熔融温度的影响，发现主要影响参数是酸碱比、碱性组分含量和硅铝比[3]。另一些研究表明，化学组成的组合参数、酸碱比和硅铝比与煤灰熔融温度之间的关联性大大升高[4-5]。熊金钰等人利用纯化学试剂改变煤灰中的铁钙比，利用BP神经网络预测了煤灰熔融温度，训练样本的相对误差小于0.39%（软化温度）和0.63%（流动温度）；检验样本中高铁低钙的ZX煤样预测温度最大误差为52℃[6]。牛苗任等人分析总结了前人的7个经验公式，指出这些经验公式适用范围窄，最后提出自己的分段拟合公式，通过验证说明该公式精度较高，但验证所使用的煤种仅为2个，同样可能存在煤种适用范围窄的缺陷[7]。杨鑫等人针对褐煤与高灰熔点煤相配的灰熔融温度预测建立了BP网络模型，发现使用组合参数进行预测比仅使用灰成分组成预测准确度高，但存在1个问题就是该模型选用的煤种较为特殊，在其他混煤的预测上可能会出现误差较大的情

况[8]。通过以上的研究成果发现，尽管人们依据不同煤种及采取不同回归方法建立预测模型，但由于煤灰的复杂性，使得一种经验公式只能适用于1个煤种。本文先对煤灰进行分类总结，然后采用多元非线性函数进行拟合，其应用推广能力相应的也会有所提高。

1 实验

1.1 煤样的选取

选用世界上具有代表性的149种硅铝比在1.8～3.0之间、碱性组分（Fe2O3+CaO+MgO+K2O+ Na2O）质量分数小于30%的煤样灰熔融温度为基础数据，其中24组数据为实验室测量所得，实验测定煤样主要灰化学组成和流动温度见表1，其余数据均从文献中收集[9-11]。

1.2 煤灰样本代表性的统计检验

煤灰化学组成成分主要为SiO2、Al2O3、Fe2O3、MnO、CaO、MgO、K2O、Na2O、P2O5、TiO2和SO3。煤灰化学组成是影响灰熔融性的主要因素，有必要客观地探讨灰成分与熔融特性间的关系，并作出判断，为建立更为准确的灰熔点预测模型奠定基础[12]。

本文主要利用相关系数法探讨煤灰中各组分与熔融性间的关系。相关性系数（R）是测定变量之间相关程度和相关方向的指标，其计算公式如下：

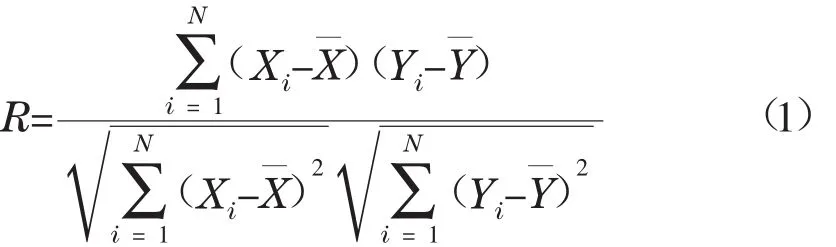
表1 实验测定煤样灰成分及流动温度

式1中R＞0时为正相关，R＜0时为负相关，R=0时为不相关。∣R∣越大表明相关程度越大。一般∣R∣≥0.7是可以接受的，∣R∣≥0.8时认为2个变量有很强的线性相关性，而当∣R∣≥0.9时是比较完美的。

计算实验选取的149种煤样灰成分各组分与流动温度间的单相关性系数，见表2所示。

表2 各组分与流动温度间的单相关性系数

根据表2中的数据，从灰成分各组分与流动温度间的相关方向角度分析，呈现正相关的有SiO2、Al2O3、K2O、P2O5和TiO2，呈现负相关的有Fe2O3、MnO、CaO、MgO、Na2O和SO3。

由表2可以看出，单一组分与煤灰流动温度的相关度较低，相关度在可接受范围（0.7≤∣R∣＜0.8）的只有SiO2和Al2O3。所以以1种组分与流动温度进行拟合是不可行的，需要进行多组分同时拟合。

1.3 最小二乘法

最小二乘法是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。有研究发现最小二乘法是目前拟合精度最高的一种方法[13]。本文将采用最小二乘法进行线性拟合。

假设给定数据点（xi，yi）（i=0，1，…，m），Φ为所有次数不超过n（n≤m）的多项式构成的函数类，现求，使得

当拟合函数为多项式时，称为多项式拟合，满足式2的pn（x）称为最小二乘拟合多项式。特别地，当n=1时，称为线性拟合或直线拟合。显然akxki-yi）2为a0，a1，…an的多元函数，因此上述问题即为求I=I（a0，a1，a2，…an）的极值问题。由多元函数求极值的必要条件，得：

式4是关于a0，a1，…an的线性方程组，用矩阵表示为：

式4或式5称为正规方程组或法方程组。可以证明，方程组（式5）的系数矩阵是一个对称正定矩阵，故存在唯一解。从式5中解出ak（k=0，1，…，n），从而可得多项式：

可以证明，式6中的pn（x）满足式1，即pn（x）为所求的拟合多项式。

2 煤灰熔融温度预测模型的建立

根据149种硅铝比在1.8～3.0之间、碱性组分质量分数小于30%的煤灰熔融数据，按照不同组分构成的影响因子进行回归研究，从而确定较为准确的回归方程，以建立较好效果的灰熔融温度预测模型。

2.1 影响因子的建立

通过表2中各组分与流动温度间的单相关性系数，可以看出灰化学组成中各组分与灰熔融温度的相关度和相关方向各不相同，由此建立影响因子FI。

将灰成分中11种组分与流动温度间的相关程度进行排序，结果见表3。计算149种硅铝比在1.8～3.0之间、碱性组分质量分数小于30%的煤灰熔融数据中各组分含量在全部煤灰中所占比重的样本均值，按照均值大小排序，结果如表4所示。

表3 煤灰组分与流动温度间的相关程度排序

表4 各组分含量在全部煤灰中所占比重的样本均值排序

由表3和表4可以看出，虽然MnO的│R│为0.553 6，但其在煤灰化学组成中所占质量分数只有0.05%，可以忽略不计，所以在研究影响因子的过程中可以舍去MnO，不做考虑。P2O5的│R│只有0.065 7，其在煤灰化学组成中所占质量分数也只有0.50%，所以也可以舍去不做考虑。经过以上分析可以将式7进行优化，得到式8。于是将表3中│R│的值带入式8中得到式9，也即为我们所需的影响因子。

利用式9计算出149组灰成分数据的FI值，计算其与灰熔融温度FT的相关系数R值为0.874 3，即说明影响因子FI与FT成正相关，其相关程度远大于单一组分（单一组分相关程度见表2）。

2.2 最小二乘法回归方程

以149种煤样的灰熔融温度数据为基础，9种煤灰成分组成的影响因子为自变量，煤灰熔融温度FT为因变量，利用最小二乘法进行一元线性拟合。由式4中n=1，可得到

，即：

将149组灰成分数据带入式10和式11中可得：

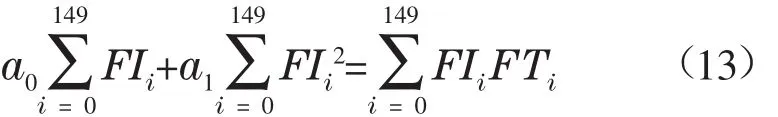
由式12和式13解得a0=118 9，a1=22.895 8。即p1（FI）=1189+22.8958×FI，也即FT=1189+ 22.8958×FI，其中FI的计算方法见式9所示，且计算其相关程度R值为0.974 2。

作者在拟合过程中，用同样方法对FI进行一元二次回归，即n=2时，回归结果p2（FI）=1003.2688+ 36.2955×FI+0.3176×FI2，其相关程度R值只有0.864 0，即说明FI和FT没有很好的二次相关关系，即一元二次回归结果不可取。

3 回归方程的验证及与经验公式的比较

为验证利用最小二乘法拟合出的方程（FT= 1189+22.8958×FI）的精确度，作者又寻找15组硅铝比在1.8～3.0、碱性组分质量分数小于30%的灰化学组成数据，以验证其精确度，结果见表5。

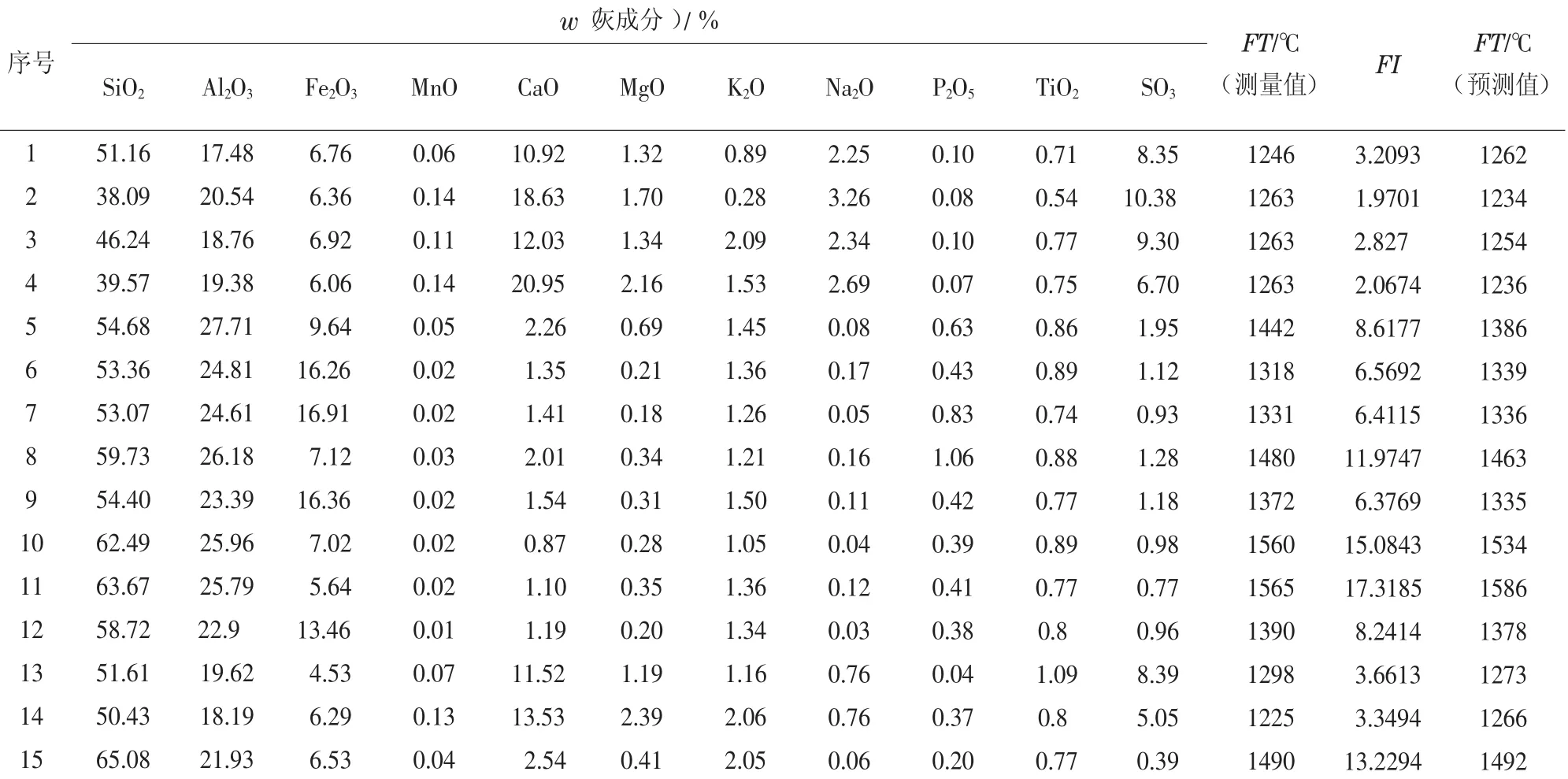
表5 验证煤样灰流动温度预测效果

将表5中灰熔融温度FT的测量值和预测值相减，得到灰流动温度预测值与测量值的偏差，结果如图1所示。

由图1可以看出，验证的15组数据的测量值与预测值误差除第5组是56℃外，其余都在±40℃以内，表明预测结果精度较好，远远优于国家标准规定的±80℃，说明此方法拟合的方程预测精度较高。

图1 灰流动温度预测值与测量值的偏差

Hakan在研究灰熔融温度与化学组成的关系时发现，煤灰流动温度关于参数呈现出很好的线性相关性，并给出如下关系式：

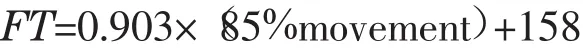
其中85%movement=1340×lg[w（Al2O3）]-251×lg [w（Fe2O3）]-106×lg[w（CaO）]-172。得到灰流动温度预测值与测量值的偏差如图2所示[14]。

图2 Hakan模型预测值与测量值的偏差

戴爱军研究了煤灰主要成分与煤灰酸碱比对灰熔融特性的影响，建立了预测流动温度的经验模型：

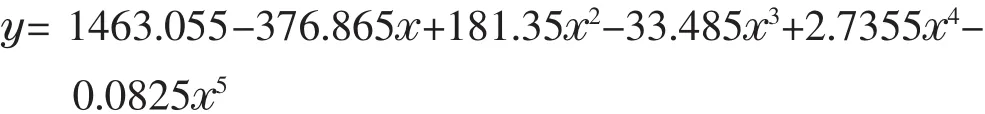
式中，x=[w（SiO2)+w（Al2O3）+w（TiO2）]/[w（Fe2O3) +w（CaO）+w（MgO）]，y表示流动温度，得到煤灰流动温度预测值与测量值的偏差如图3所示[15]。

由图2和图3可以看出，Hakan模型和戴爱军模型的预测值与测量值的偏差，虽然大部分值在国标规定的±80℃以内，但偏差大部分在±50℃以外，有些值甚至达到了300多，可见其预测精度不够。

图3 戴爱军模型预测值与测量值的偏差

4 结论

（1）借助现代统计理论对149种煤灰熔融温度分析表明，煤灰化学组成中各个氧化物与熔融温度之间存在各不相同的关联性，但是单一氧化物与熔融温度的关联性不大；引入影响因子FI后的相关性可以达到0.874 3，说明综合考虑后的FI与熔融温度有较大的相关性。（2）以FI为自变量、FT为因变量进行最小二乘法拟合，线性拟合要优于一元多次拟合，线性拟合的拟合度达到了0.974 2，拟合方程为FT=1189+ 22.8958×FI，其中FI的计算方法见文中式9所示，且其预测精度要优于传统经验公式。

[1]Song W，Tang L，Zhu X，et al.Flow properties and rheology of slag from coal gasification[J].Fuel，2010，89（7）：1709-1715.

[2]贺根良，门长贵.气流床气化炉操作温度的探讨[J].煤化工，2007（4）：8-11.

[3]Vargas S，Frandsen FJ，Dam-Johansen K.Rheological properties of high temperature melts of coal ashes and other silicates[J].Progress in Energy and Combustion Science，2001，27（3）：237-429.

[4]Song Wenjia，Tang Lihua，Zhu Xuedong.Effect of coal ash composition on ash fusion temperatures[J].Energy& Fuels，2010，24（1）：182-189.

[5]程翼.助熔剂对淮南矿区煤灰熔融特性及粘温特性的影响[D].淮南：安徽理工大学，2006.

[6]熊金钰，李寒旭，曹祥，等.神经网络法预测煤灰中铁钙比与灰熔融温度的关系[J].2015，44（2）：209-213.

[7]牛苗任，孙永斌，林碧华，等.煤灰熔融温度计算公式的研

10.13752/j.issn.1007-2217.2017.02.007

2017-04-25