改进的FB法对抛物面天线远场的优化分析
2017-07-07陆大庆宋开宏
陆大庆, 宋开宏
(安徽大学 计算智能与信号处理教育部重点实验室,安徽 合肥 230039)
改进的FB法对抛物面天线远场的优化分析
陆大庆, 宋开宏
(安徽大学 计算智能与信号处理教育部重点实验室,安徽 合肥 230039)
传统的物理光学(physical optics,PO)法是对抛物面上电流直接积分来计算远场的电场值,傅里叶贝塞尔(Fourier-Bessel,FB)法是用有限项级数来逼近积分电流,在保证准确性的同时提高了计算效率。为进一步提高计算效率,文章结合了PO法和FB法,剥离远场公式观察角的同时在傅里叶有限项级数的基础上再次进行泰勒公式展开,忽略泰勒公式中高阶无穷小项,优化了远场计算效率,并给出了3种方法下抛物面天线远场的电场计算结果、精度、运行时间对比。数值计算结果表明,优化后的FB法在保证计算准确性的前提下计算效率得到了明显的提高。
抛物面天线;傅里叶贝塞尔(FB)法;泰勒展开;物理光学(PO)法
0 引 言
在计算抛物面天线的远场时,传统的物理光学(physical optics,PO)法和傅里叶贝塞尔(Fourier-Bessel,FB)法都能有效地计算天线的远场特性。PO法是直接对抛物面的面上电流积分,随着天线尺寸和观测平面的增加,PO法的计算时间将会呈现指数增长[1-2];FB法是在PO法的基础上对抛物面的面上积分电流进行傅里叶级数展开,用有限项级数代替积分电流,当FB法的项数信息能足够反映面上电流时,远场的计算精度将得到保证,同时又大大提高了计算效率,文献[3-5]对该方法求解电磁场问题做了深入的分析,并且简明扼要地介绍了计算方法和结果。
本文在上述研究的基础上,将抛物面上的积分电流公式中与远场有关的观察角剥离出来,以减少求解傅里叶级数时的重复运算[6-7],并对原有傅里叶级数公式再次进行泰勒级数展开,忽略泰勒级数中高阶无穷小项;将计算结果与传统的PO法和FB法进行比较,结果表明,该方法在保证计算准确性的同时降低了运算量,提高了运算速度[8]。
1 理论分析
抛物面天线模型如图1所示,右侧是天线电流投影在XOY平面的口径图,投影区域A的直径为D。区域B包含区域A。

图1 抛物面天线模型图
抛物面天线的远场辐射公式为:

(1)
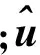
利用傅里叶算法可有效计算(1)式中Emn,由于电流Jeg与远场观察点直接相关,需要将其从公式中的观察角中剥离出来,使得Emn与远场观察点不相关,从而推导出高度收敛的级数来表示远场方程,提高天线远场的运算效率。选择对称抛物面的一般方程为:
(2)
其中,F为抛物面中心到坐标原点的距离。
剥离Emn与观察点的联系,需将等效电流中Jeg的观测角θ项剥离,注意Jeg中与观察角相关的因子exp(jkzcosθ)可以写成:
(3)
将(2)式、(3)式代入(1)式得:
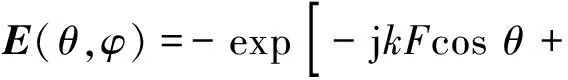
exp[jk(u-u0)x+jk(v-v0)y]dxdy
(4)
其中,Js为Jeq投影到XOY面的等效电流。
再代入(4)式展开可得:
(5)
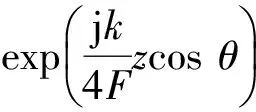
(6)
为确保计算精度的同时提高计算速度,需要对傅里叶级数m、n设定合适的值。由于计算模型的最大期望方向是在Z轴方向上,故cosθ0=1,抛物面天线的远场公式进一步优化后为:
(7)
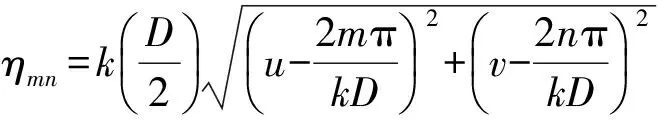
2 结果与验证
为验证本文方法的准确性,分别采用优化前、后的2种傅里叶贝塞尔函数来计算偶极子天线阵列在经过抛物面天线反射后远场的电场值。
传统PO法和FB法计算上述模型得到的结果如图2所示,其中横坐标为远场观察平面中心轴上的观察点位置。计算结果验证了传统PO法和FB法在该模型下的适用性。

图2 PO法与FB法计算的抛物面天线远区电场
本文方法与传统FB法计算上述模型得到的结果如图3所示。由图3可知,本文改进的FB法和传统FB法在计算结果上基本吻合。两者之间的误差来自于:① 傅里叶变换时使用有限项级数替代无限项级数,牺牲计算精度所带来的截断误差[9];② 在观测角处泰勒级数展开仅保留了前2项,随着观察处的距离变化,省略高阶项的泰勒级数的展开所引起的误差也在加大。但是通过选择适当的傅里叶变换的有限项级数和泰勒级数[10],可以使得本文改进的FB方法在误差允许的范围内基本满足计算精度,同时大大提高了计算效率。

图3 FB法与本文方法计算的抛物面天线远区电场
由于远场观察角和观察平面是直接相关的,以抛物面的轴向方向为远场观测平面的中心,以观察平面大小为单一自变量,比较上述方法在计算时间上的优势。
PO法、FB法和本文方法在计算抛物面天线远场所需的运行时间对比如图4所示。由图4可知,本文方法在计算抛物面天线远场的效率上高于PO法和PB法,且随着观测平面面积的增加,这种差异将会愈加明显。

图4 3种方法的运行时间对比
3 结 论
本文基于抛物面天线的模型,在传统的FB法基础上,将抛物面天线的面上电流中与远场观测点相关的因子剥离,同时对面上电流进行泰勒公式展开,忽略泰勒展开式中高阶无穷小项。这种改进的的FB法,在误差范围内保证计算准确性的同时大大提高了计算效率,从而为快速分析大型抛物面天线的远场提供了一种有效途径。
[1] 钟顺时.微带天线理论与应用[M].西安:西安电子科技大学出版社,1991.
[2] 朱艳菊,江月松,张崇辉,等.应用改进的物理光学法和图形计算电磁学近似算法快速计算导体目标电磁散射特性[J].物理学报,2014,63(16):178-184.
[3] 刘旭峰,刘少东,张福顺,等.宽角扫描双反射面天线的方向图分析[J].西安电子科技大学学报(自然科学版),2005,32(1):80-83.
[4] MITTRA R,KO W L,SHESHADRI M S.A transform technique for computing the radiation pattern of prime-focal and cassegrainian reflector antennas[J].IEEE Transactions on Antennas and Propagation,1982,30(3):520-524.
[5] LEE S W,MITTRA R.Fourier transform of a polygonal shape function and its application in electromagnetics[J].IEEE Transactions on Antennas and Propagation,1983,31(1):99-103.
[6] SCOTT C.Modern methods of reflector antenna analysis and design[M].Boston:Artech House on Demand,1990.
[7] 张旺,王黎莉,闰丰.双反射面天线偏焦问题的解决方法分析[J].无线电工程,2011,41(8):35-37.
[8] KILDAL P S.Analysis of numerically specified multireflector antennas by kinematic and dynamic ray tracing[J].IEEE Transactions on Antennas and Propagation,1990,38(10):1600-1606.
[9] LEE S W,CRAMER P,WOO K,Jr,et al.Diffraction by a arbitrary subreflector:GTD solution[J].IEEE Transactions on Antennas and Propagation,1979,27(3):305-316.
[10] GUPTA B,BHATTACHARYYA I,BANDYOPADHYAY A.Identification of anomalies in paraboloid antenna reflector surface from its power radiation patterns[C]//A Workshop on Advanced Antenna Technology.[S.l.]:IEEE,2010:1-9.
(责任编辑 胡亚敏)
Optimization analysis of far field of parabolic antenna by using improved Fourier-Bessel method
LU Daqing, SONG Kaihong
(Key Laboratory of Intelligent Computing and Signal Processing of Ministry of Education, Anhui University, Hefei 230039, China)
The traditional method of physical optics(PO) is the method of the direct integral of current on the parabola to calculate the electric field value of the far field. The Fourier-Bessel(FB) method is to use limited series to approximate integral current, and is able to ensure accuracy and improve the calculation efficiency at the same time. In order to further improve the efficiency of calculation, this paper combines the two methods mentioned above. It is about stripping of the observation angle of far field formula and expanding the Taylor formula again based on the Fourier limited series simultaneously. High order infinitesimal series of the Taylor formula is ignored, thus optimizing the far field computation efficiency. The comparison of calculation results, precision and running time for the far field electric field of the parabolic antenna under three methods is presented. The numerical calculation results show that the optimized method of FB improves the calculation efficiency obviously while ensuring accuracy.
parabolic antenna; Fourier-Bessel(FB) method; Taylor expansion; physical optics(PO) method
2015-08-07;
2015-10-08
国家自然科学基金资助项目(61471001;51277001);安徽省自然科学基金资助项目(1508085JD03;1508085QF130)
陆大庆(1990-),男,安徽合肥人,安徽大学硕士生; 宋开宏(1969-),男,安徽芜湖人,安徽大学副教授,硕士生导师.
10.3969/j.issn.1003-5060.2017.05.017
TN82
A
1003-5060(2017)05-0656-04
