基于模糊非线性状态误差反馈策略的EPS回正控制

陈久闪, 赵林峰, 祖春胜

(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)

基于模糊非线性状态误差反馈策略的EPS回正控制

陈久闪, 赵林峰, 祖春胜

(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)

为了解决电动助力转向(electric power steering,EPS)系统回正控制中快速性与准确性之间的矛盾,提升回正控制的稳定性,文章针对PID控制中积分环节的不利影响及滑模变结构控制(sliding mode control,SMC)较为依赖精确数学模型的问题,采用了非线性状态误差反馈(nonlinear state error feedback,NLSEF)的EPS回正控制策略;对NLSEF的参数采用模糊化控制调节,以转向盘的转角及角速度作为输入变量,建立回正控制策略模型。台架试验结果对比表明,参数模糊化控制的NLSEF方案明显改善了EPS的回正性能,同一车速条件下,不论转向盘初始状态如何,都能快速、准确地操纵汽车回正。

电动助力转向(EPS);回正;非线性状态误差反馈(NLSEF);模糊控制

近年来,由于电动助力转向 (electric power steering,EPS) 相对于传统液压助力具有节约能源、结构紧凑、质量轻、便于布置、操纵稳定性高等优点而广泛应用于汽车上[1]。研究人员在EPS主动回正功能开发过程中发现,系统具有很多不确定因素和外部扰动,例如，汽车的载荷变化、轮胎磨损、轮胎压力改变以及汽车在行驶时受到路面不平度的激励等，这些均可能导致系统参数的变化,从而引发系统的不确定性干扰[2]。

传统PID控制算法的最大优点是面向过程而不依赖系统模型,但在EPS系统不确定因素和外部扰动影响下,较难实现转向盘在不同的角度下都能准确、快速地回到中心位置[3]。同时,工程实践也表明,积分信号的引入使闭环系统变得迟钝,容易产生振荡,限制了转向盘快速回正。

文献[4]提出基于滑模控制(sliding mode control,SMC)的回正控制策略,滑模控制算法对模型参数的不确定性和外界扰动具有很好的鲁棒性,且方法简单、易于实现，但滑模控制的效果依赖于系统模型的精确性。

为了更好地解决回正控制中快速性和超调量之间的矛盾,扩大控制算法的适用范围,本文提出基于模糊非线性状态误差反馈(nonlinear state error feedback,NLSEF)的回正控制策略。NLSEF控制是一种既不依赖于对象模型,又具有较强鲁棒性的控制算法,可显著地提高反馈控制的效果[5-6]。根据“小误差,大增益;大误差,小增益”的原则,选取适当线性区间,并进行分割,同时对相关参数进行模糊化处理,可以获得快速准确的调节效果[7]。此外,采用非线性反馈,系统静态误差以数量级方式减小,提高了控制精度。

1 系统模型建立

1.1 EPS模型

由于回正控制策略是基于电动助力转向系统动力学模型设计的,需要建立EPS动力学模型。EPS的结构简图如图1所示。

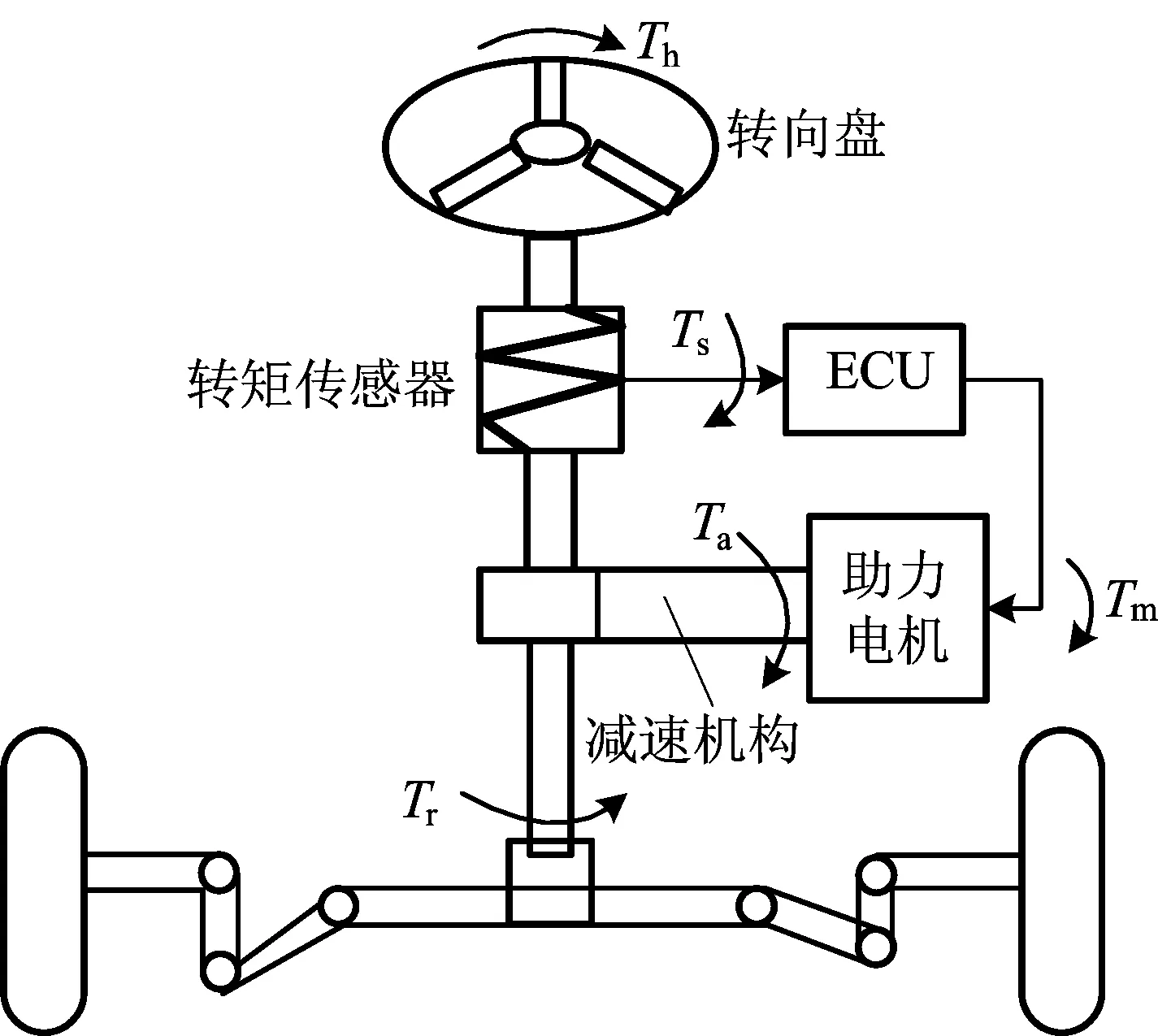
图1 EPS系统动力学模型

动力学方程如下:

(1)

(2)

Tm=KtI

(3)

(4)

其中,Je为转向柱等效转动惯量;Be为转向柱阻尼系数;θp为转向小齿轮转角;Ta为电机助力转矩;G为电机到转向轴的传动比;N为转向轴到前轮的传动比;Th为作用在转向盘上的转向力矩;Tr为作用于转向小齿轮的转向力矩;Tm为电动机的电磁转矩;Bm为电动机黏性摩擦系数；Jm为电动机转动惯量;θm为电动机转角;Kt为电机电磁转矩系数;I为控制电流;TAlgin为折合到转向小齿轮的回正力矩;Mz为前轮自回正力矩;Msz为重力引起的回正力矩;M为车辆两前轮回正力矩之和;Tf-rp为转向系摩擦力矩;σ(t)为与路面有关的干扰函数。

1.2 轮胎回正力矩模型

轮胎与路面之间的接触力在车身航向直角坐标上的分解如图2所示。图2中i=1,2,3,4,分别表示左前轮、右前轮、左后轮、右后轮,下文i的含义同此。

图2 轮胎与地面作用力

假设同轴左、右车轮的转向角相同,前轮转向,即δ1=δ2=δf,δ3=δ4=0。由图2分析可以得出:

(5)

其中,i=1,2,3,4;Fx、Fy分别为纵向力、侧向力;Fxw、Fyw分别为轮胎纵向力、侧向力;δ为轮胎转角;δf为前轮转角。

忽略惯性阻力偶矩和空气升力作用,则有:

(6)

(7)

其中,m为整车质量;g为重力加速度;ωr为横摆角速度;a、b分别为前、后轮到质心的距离;d为轮距;vx、vy分别为汽车在横向、纵向上的车速;W为轮胎的垂直载荷;l、h分别为轴距、车辆质心高度;α为轮胎侧偏角。

对轮胎自回正力矩分析采用Dugoff非线性轮胎模型[8],设左、右轮胎侧偏刚度相同,4个轮胎纵向刚度相同,其表达式为:

(8)

(9)

其中,λ为轮胎的纵向滑移率;τ为车速附着系数影响系数;Cα、Cs分别为轮胎的侧偏刚度、纵向刚度;μ为轮胎与路面之间附着系数;ζ为轮胎动态参数;ψ(ζ)为与ζ有关的函数。

轮胎纵向力、侧向力由轮胎与地面接触变形而产生,视其动力学模型为一阶惯性环节,有

(10)

其中,τx、τy分别为轮胎纵向力、侧向力时间常数;LRx、LRy分别为轮胎纵向、侧向松弛长度。

轮胎自回正力矩由轮胎侧向力和轮胎拖距产生。轮胎拖距为主销后倾引起机械拖距与气胎拖距之和。机械拖距tm可视为一定值,而气胎拖距tp受轮胎侧偏刚度、路面附着系数及侧偏角等因素影响,其初值为tp0,则tp表达式为:

(11)

(12)

重力引起的回正力矩Msz表现为,将转向盘打到某一角度后,松开转向盘后,转向盘在前轴轴荷、前轮定位参数引起的回正力矩(可称之为“重力引起的回正力矩”)作用下向中间位置回复一定角度,表达式为:

(13)

其中,Dn、φ分别为主销内倾量、主销内倾角;Wf为前轴载荷。

2 常规回正控制算法

2.1PID控制

PID控制逻辑如图3所示。

目前大部分回正控制仍然是基于转向盘转角的PID控制。采用转角传感器测量的转向盘实际转角作为回正控制器的输入变量,通过PID调节获得目标回正控制电流,具体公式为：

(14)

其中,θs为转向盘实际转角;KP、KI、KD分别为比例、积分和微分系数。

图3 PID控制逻辑

2.2SMC控制

SMC控制逻辑如图4所示。

图4 SMC控制逻辑

2.1.1 等效滑模模块设计

将回正控制系统定义为实际转向盘转角跟踪所需的目标转角,跟踪误差为e。为了使EPS系统的实际转向盘转角更好地跟踪参考模型的转角,误差动态特性可以由一个切换面来确定,设该切换面s=0。选择切换函数为:

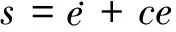
(15)

其中，c为误差与误差变化率之间的相对权重系数。

根据文献[4]中EPS等效转向系统模型,可得:

(16)

其中,J、B分别为整个转向系统等效转动惯量和阻尼系数。

(17)

根据滑模等效条件,等效控制Ieq为:

(18)

2.1.2 切换控制模块设计

(19)

其中,η≥max |d(t)|,d(t)为系统扰动函数。

SMC控制中目标回正控制电流为:

(20)

3 NLSEF模糊控制

将NLSEF控制与模糊控制相结合,NLSEF控制为主控制策略,模糊控制起辅助作用,设μ1、μ2、μ3、μ4为模糊调节因子。NLSEF参数模糊化控制逻辑如图5所示。

图5 模糊NLSEF控制逻辑

3.1NLSEF控制设计

NLSEF控制策略利用转向盘转角和角速度输入与输出之间的误差,通过非线性组合配置来确定控制量。对于回正控制问题,设定参考输入转向盘转角和角速度均为0,定义状态误差为:

(21)

则NLSEF回正控制电流为:

(22)

考虑到实际应用中控制芯片的运算能力问题,本文将非线性函数fal(ei,ki,δi)设计为:

(23)

其中,i取值为1或2;sat(ei,δi)为关于误差饱和值δi的饱和函数,计算公式为：

(24)

(22)式实际上是非线性状态误差反馈PD控制律,β1、β2分别为相应的比例因子和微分因子。

对于比例作用,在小误差时应采用大增益,大误差时应采用小增益,因此比例项中,取fal(ei,ki,δi)函数中的k为30。

对于微分作用,在微分误差小时应采用小增益,微分误差大时应采用大增益,因此微分项中,取fal(ei,ki,δi)函数中的k为100。

3.2 模糊控制器设计

模糊控制可以按照经验或者试验数据制定控制规则来控制受控对象,不依赖于数学模型,因而对系统参数的变化不敏感,具有很强的鲁棒性,常应用于非线性、时变和具有结构不确定性的系统[9],具体设计如下:

(1) 转向盘实际转角θs绝对值大于200°时,μ1=2,μ2=1,μ3=0,μ4=0。

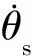
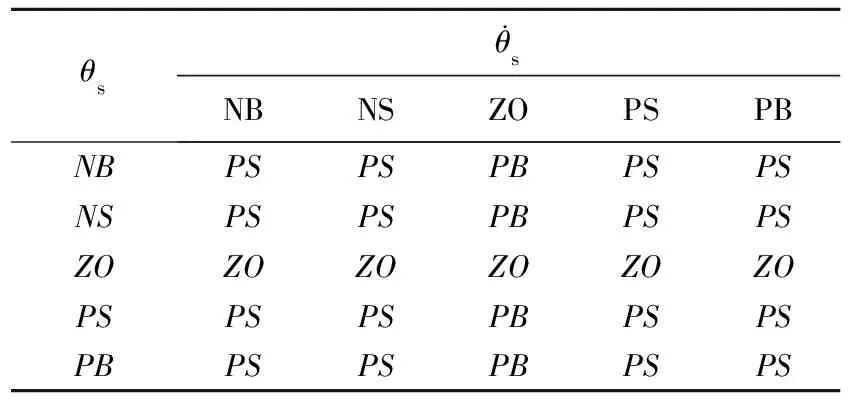
表1 μ1、μ2模糊控制规则

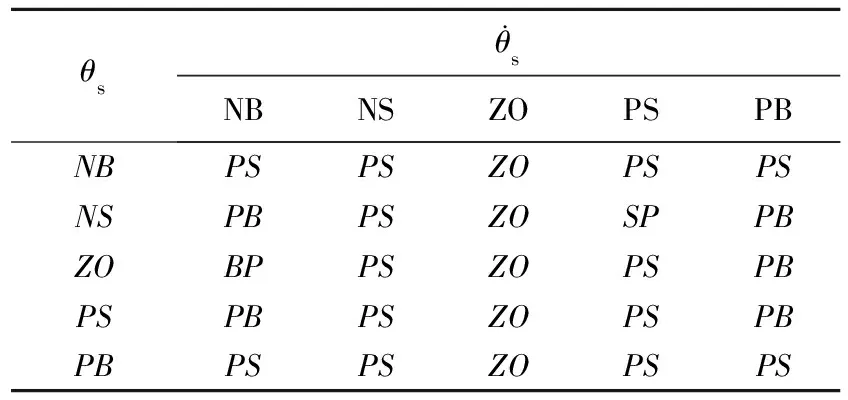
表2 μ3、μ4模糊控制规则

将μ1、μ2、μ3、μ4代入NLSEF反馈控制器模型中,即可得回正控制电流为:

(25)

4 回正试验

为验证所设计的回正控制策略的效果,本文进行了EPS台架试验。分别对上述4种回正控制策略进行4种不同初始角度的回正试验,4次试验的初始转向盘转角分别为50°、100°、200°、400°。

台架试验涉及的EPS系统参数如下:

Je=0.06 kg·m2,Be=0.2 N·m·s,

G=16.5,Jm=0.003 3 kg·m2,

Bm=6 μN·m·s,N=20,

Kt=0.05 N·m/A。

记录转向盘转角随时间变化的曲线,每种转角下采集3组试验数据,其结果见表3所列。其中1组数据曲线如图6所示。

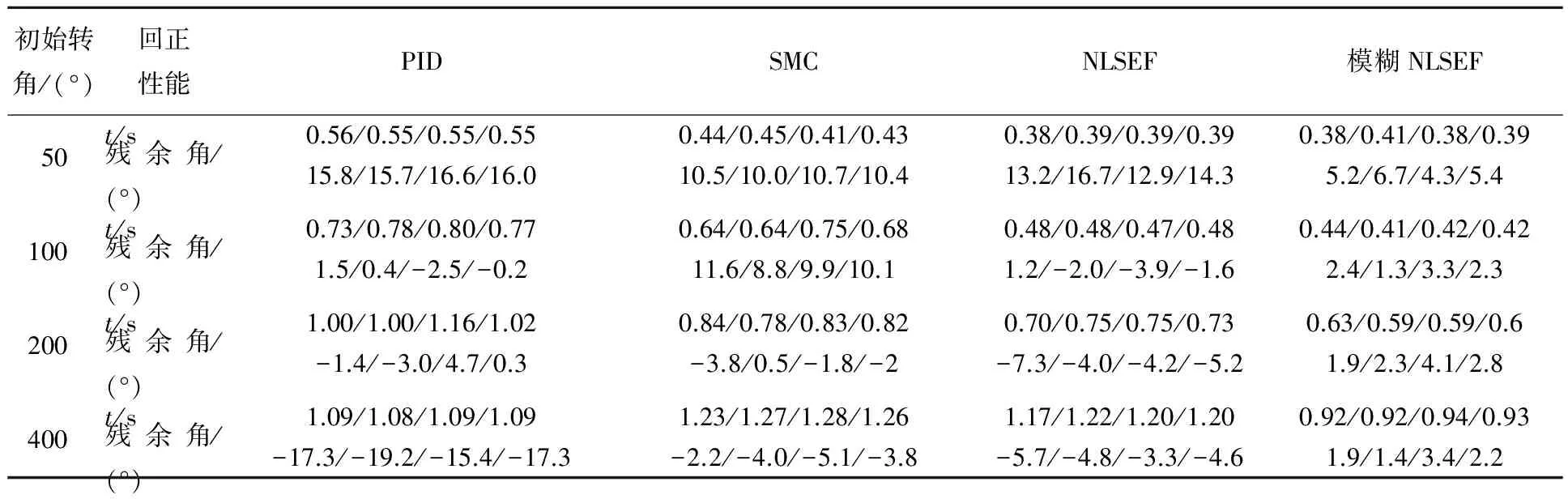
表3 回正持续时间和回正残余角

注:表中数据依次为第1～3组试验数据及3组试验数据的平均值。

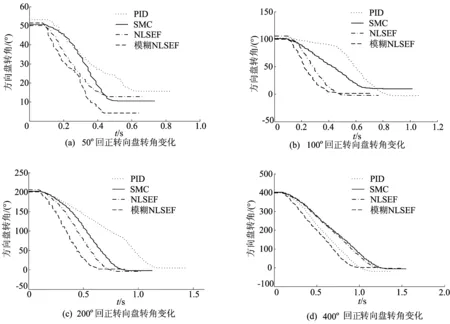
图6 4种回正控制策略试验效果对比

对表3及图6结果进行分析可知:

(1) 从回正过程中转向盘速度上看,模糊NLSEF回正控制在各个转向盘转角下的回正响应时间均小于其他回正策略;NLSEF和SMC控制相对于传统PID在小转向盘转角下回正速度也有明显提升,但是在大转向盘转角下效果不明显。

(2) 从转向盘残余角可以看出,模糊NLSEF控制在不同初始转向盘转角下,残余角均小于其他3种控制策略,试验结果稳定,且无回正不足和超调现象;传统PID控制效果较差,在小角度下回正不足,大角度下回正超调,控制结果不稳定,易受外界干扰影响;NLSEF和SMC控制相对于PID效果较好,控制结果也比较稳定;但是,小角度回正不足,大角度回正超调现象仍然存在。

5 结 论

(1) 本文提出的回正控制策略不依赖于系统模型,提高了EPS系统的自适应性和鲁棒性,适用范围更广泛。

(2) 采用模糊控制器调节NLSEF的控制参数,更好地解决了EPS回正快速性与超调量之间的矛盾。台架试验结果证明该回正策略的性能优于其他3种策略,并且无论方向盘初始状态如何,均可实现转向盘快速、准确地回至零位,回正控制效果稳定。

(3) 因为不同车型车轮定位参数及轮胎参数不同,回正力矩和回正阻力矩有较大差别,所以需进行相关测试以确定回正所需要的特征参数,此问题尚待进一步深入研究。

[1] 周廷明,刘志辉,李梦奇,等.电动助力转向系统及其关键技术[J].机床与液压,2012,40(7):176-178，209.

[2] 王华强,袁浩,杨滁光.自适应模糊神经网络在EPS中的应用[J].合肥工业大学学报(自然科学版),2011,34(2):188-191.

[3] 赵万忠,施国标,林逸,等.电动客车电动助力转向回正控制策略[J].江苏大学学报(自然科学版),2011,32(1):28-31.

[4] 赵林峰,陈无畏,刘罡.电动助力转向系统全工况建模及试验验证[J].农业机械学报,2009,40(10):1-7.

[5] 黄庆,黄守道,伍倩倩,等.基于模糊自抗扰控制器的永磁同步电动机伺服系统[J].电工技术学报,2013,28(9):294-301.

[6] 黄一,薛文超.自抗扰控制:思想、应用及理论分析[J].系统科学与数学,2012,32(10):1287-1307.

[7] 李绍松,宗长富,吴振昕,等.电动助力转向主动回正控制方法[J].吉林大学学报(工学版),2012,42(6):1355-1359.

[8] DUGOFF H,FANCHER P,SEGAL L.An analysis of tire traction properties and their influence on vehicle dynamic performance[J].SAE Transcations,1970,79:341-366.

[9] 陈克,万思彤,李铎.电动助力转向系统随动特性仿真[J].中国工程机械学报,2013,11(1):6-10.

(责任编辑 张淑艳)

EPS return control based on fuzzy NLSEF control method

CHEN Jiushan, ZHAO Linfeng, ZU Chunsheng

(School of Automobile and Traffic Engineering, Hefei University of Technology, Hefei 230009, China)

In order to enhance the return stability of electric power steering(EPS) system, and resolve the contradiction between the rapidity and accuracy during the return control, the fuzzy nonlinear state error feedback(NLSEF) control is proposed to eliminate the negative effect of the integral link in PID control and solve the problem that sliding mode control(SMC) is more dependent on the exact mathematical model. The NLSEF parameters are adjusted by fuzzy control. Taking the steering wheel angle and angular velocity as the input variables, the return control strategy model is established. The bench test results show that the proposed control strategy can improve the return performance of EPS. At the same vehicle velocity, the return control system can quickly and accurately control the steering wheel back to the mid-position no matter what the initial steering wheel angle is.

electric power steering(EPS); return; nonlinear state error feedback(NLSEF); fuzzy control

2015-12-15；

2016-03-25

安徽省自然科学基金资助项目(2013AKZR0077);安徽省自然科学基金青年资助项目(1508085QE92)和中央高校基本科研业务费专项资金资助项目(JZ2014HGBZ0374)

陈久闪(1992-),男,安徽六安人,合肥工业大学硕士生; 赵林峰(1979-),男,安徽宣城人,博士,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.05.004

U463.4

A

1003-5060(2017)05-0595-06