基于邻域搜索的粒子群动态优化算法

申鼎才, 胡声洲

(1.赣南师范大学 数学与计算机科学学院,江西 赣州 341000; 2.湖北工程学院 计算机与信息科学学院,湖北 孝感 432000)

基于邻域搜索的粒子群动态优化算法

申鼎才1,2, 胡声洲1

(1.赣南师范大学 数学与计算机科学学院,江西 赣州 341000; 2.湖北工程学院 计算机与信息科学学院,湖北 孝感 432000)

常规的粒子群优化(particle swarm optimization,PSO)算法在求解动态环境下优化问题时，由于其收敛性而失去对最优解的跟踪能力。为了更好地增加种群的多样性,以保证算法更好地追踪动态环境下最优解的变化,文章提出一种基于邻域搜索的粒子群动态优化算法(neighborhood search particle swarm optimization,NSPSO)。在每一演化代中对个体依适应值从大到小排序,并对排序后的个体按从大到小的顺序以一定的比例分配Leader、Follower、Scouter 3种不同的角色,不同角色的个体采用不同的更新策略,使得算法在维持一定开发能力的同时维持较强的探索能力。通过对移动峰问题的实验发现NSPSO算法具有较小的离线误差,且离线误差受变化强度的影响均小于其他用于比较的算法,从而验证了NSPSO算法能够有效地跟踪动态环境下最优解的变化。

粒子群优化(PSO);动态优化问题;邻域搜索;多角色;演化计算

0 引 言

粒子群优化(particle swarm optimization,PSO) 算法[1]是一种基于群体智能的演化算法,由于PSO算法参数少、收敛速度快,在大规模优化问题的求解中取得了很好的性能[2],因此自提出以来得到了广泛的应用,但大多数研究成果是基于静态优化问题。然而实际应用中很多优化问题是动态的,即被优化问题的目标函数、约束条件、环境参数中的1个或多个会随着时间的变化而改变。因此算法的目的不再是获得优化问题的最优解,而转变为算法对最优解在搜索空间内的追踪能力,从而给传统的PSO带来新的挑战。因为随着算法的不断演化,种群中的粒子逐渐收敛到最优解附近,种群多样性减小,从而失去对环境变化的跟踪能力。

为了使PSO在整个算法的执行期间维持较大的种群多样性,同时又能更快地追踪到最优解的变化,本文提出一种基于邻域搜索的粒子群动态优化算法(neighborhood search particle swarm optimization,NSPSO),通过对移动峰测试函数(move peak benchmark,MPB)的实验,验证了该算法能很好地跟踪动态环境的变化。

1 相关研究

在动态环境下,为了使算法能较好地跟踪最优解的变化,研究者们提出了各种策略来提高演化算法在动态环境下的性能,如基于记忆的机制[3]采用保存算法获得的最优解并把该解参与到后续的演化过程中,这种策略在周期性变化的环境中能够获得较好的动态性能。另外在算法的演化过程中维持较高的种群多样性也是算法获得较高跟踪最优解变化能力的有效策略。典型的有随机移民策略[4]、超变异策略[5]等。随机移民策略通过在演化过程中引入随机生成的新个体并按一定比例替换种群中已有个体。具体替换策略主要分随机替换和替换种群中适应值最差个体2种;超变异策略则在演化过程中一旦检测到环境发生变化，则采用加大变异概率,以此来增加种群多样性,从而使算法能更好地适应变化的环境。此外,采用多种群算法,并在不同的种群采用不同的搜索策略在动态的环境下也取得了很好的效果[6-7]。近年来,PSO应用于动态环境下优化问题的求解受到广泛关注[8]。

2 基于领域搜索的动态粒子群算法

2.1 算法基本思想

在PSO群体中,个体的运动方向受其自身历史最优位置和群体中全局最优位置影响而不时作出调整。在常规的PSO中,随着演化的进行,种群中的所有粒子将聚集在最优个体附近,此时如果最优解的位置发生变化,则算法将失去探索新解的能力[9]。在演化动态优化领域,通过维持种群多样性来达到跟踪最优解的变化是一类有效的策略。因此,如果在算法的演化过程中能引入相应策略来保持种群的多样性,使得算法在维持一定开采能力的同时,又能维持较高的探索能力。受文献[10]和人工蜂群算法[11]中把个体分为不同角色进行演化的思想启发,本文提出NSPSO算法。该算法在每一演化代中,种群中的粒子依适应值从大到小排序,并按一定比例分成3类角色,各角色在更新的过程中采用不同的更新策略。本文把PSO中个体分为Leader、Follower和Scoute 3类角色,其中Leader为当前种群中适应值排在最前面一定比例的个体,其个数可以是1个到多个,紧接着Leader个体为Follower角色个体,其数量也是按一定比例设定,种群中剩余的个体为Scouter个体。Leader个体的更新公式如下:

(1)

其中，xL为当前Leader角色中不同于个体i的随机选择的个体;xk为Leader角色个体中不同于i、L的个体;φi为[-1,1]范围内的一个随机数;R为邻域半径常数。

Follower个体的更新策略与Leader更新类似,所不同的是(1)式中xL设为Leader角色个体中随机选择的个体,即Follower个体围绕Leader个体一定邻域内搜索最优值。Scouter角色更新采用常规的PSO更新策略[2]。即Scouter在其余搜索区域随机搜索。

2.2 算法实现

NSPSO算法实现的基本步骤如下:

(1) 初始化,t←0,在目标搜索空间内随机生成N个个体种群P(t),设置Leader个体和Follower个体占种群大小的比值RL和RF。

(2) 对种群P(t)进行评估,并依适应值由高到低进行排序。

(3) 根据预设的RL和RF依适应值从高到低的顺序按比例分配Leader个体和Follower个体,其余个体分配为Scouter个体。

(4) 分别对Leader、Follower、Scouter角色个体执行更新操作,并同时更新个体历史最优值和全局最优值。

(5) 若终止条件不满足,则P(t)←P(t+1),t←t+1,转步骤(2);否则算法终止。

本文比较了NSPSO算法与带电粒子群优化算法[12](charged particle swarm optimization,CPSO)、随机移民粒子群优化算法(random immigrant particle swarm optimization,RIPSO)和常规PSO(standard PSO,SPSO)在动态优化问题中的性能。

3 实验结果与分析

MPB[13]被经常用来测试动态优化算法的性能。MPB具有多维、多峰的特点,具有m个峰的n维函数可表示为:

F(x,t)=maxB(x),

(2)

其中,B(x)为一个非时变的基准函数;P为定义峰形状的函数,每经历Δe次评估,各个峰的位置pi、宽度wi、高度hi均依一个高斯变量σ∈N(0,1)变化,峰位置移动由一个长度为s的随机变量控制,s的大小决定环境变化的强度,Δe的大小则决定环境变化的频率。

PSO相关的参数及用于比较的算法中参数设置为:惯性权重w设置为0.729 8,学习因子c1=c2=2.05。 CPSO中,Q=0.1,pcore=2.187,prepel=31.5;RIPSO中迁移率为种群大小的10%;NSPSO中各角色比例分配经初步实验得出Leader、Follower、Scouter之比为0.04∶0.5∶0.46时取得较好性能,(1)式中邻域半径R设为1.62。所有算法中种群大小均为50。MPB的设置则依文献[13]中第2种情形设置。主要参数设置为:峰的个数m=10,s=1.0,Δe=5 000。同时对所选算法在其他变化强度s下离线误差性能作了分析。

在动态环境中,最优解随着环境的变化而变化,算法不再以求得唯一最优解为最终目标,而是以算法对最优解的跟踪能力来衡量算法的性能。由于选定的MPB测试函数每次环境变化中实际最优值是已知的,因此本文采用离线误差,即每次评估时实际最优值和算法求得的最优解的误差平均值,其计算公式为:

(3)

其中,e(t)为到第t次评估时最优解的误差；T为总的评估次数。

3.1 离线误差结果和分析

在随机的环境变化中,函数的适应值曲线随机变化,各个峰的高度、宽度和位置随机变化,函数最优解的位置也随之发生变化。 在上述设定参数下,各算法采用相同随机数种子生成移动峰进行测试,实验中种群个体采用不同的随机数种子随机生成,对MPB运行30次取平均值,所获得的离线误差及标准差见表1所列。

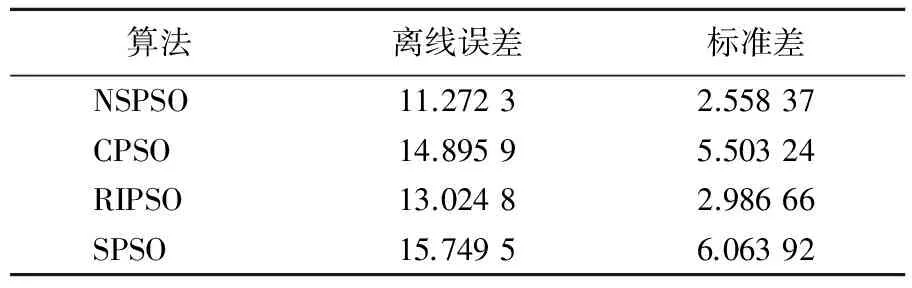
表1 离线误差及其标准差

同时,为了更好地比较算法在执行过程中的性能,各算法离线误差与迭代次数的关系如图1所示。

图1 各算法离线误差性能曲线

从表1和图1可以看出,NSPSO离线误差明显优于其他3种选定的算法,且算法比较稳定,其标准差在4种算法中最小。SPSO算法离线误差最大,标准差也是4种算法中最大的。可以看出,常规的PSO算法虽然在静态环境下取得了较好的性能,但在动态环境下,由于算法在迭代后期会收敛于最优解,从而失去对最优解的动态跟踪。在参与比较的4种算法中,RIPSO的性能比较接近NSPSO,由此可以得出,虽然常规的PSO算法由于受全局最优解的影响而失去对动态环境的跟踪能力,但通过在其演化过程中引入一定数量的新个体即可以比较好地跟踪最优解的动态变化。CPSO在4种算法中动态性能居第3的位置,由于算法中参数的设置对其动态性能的影响较大[14],就本文选定的参数来看,其动态性能略优于常规的PSO算法,获得该算法更好性能的参数设置有待于进一步的研究。

此外,从图1可以得出,在迭代初期,NSPSO离线误差要劣于其他算法,大约经过10次环境变化后,NSPSO的优势逐渐显现出来,离线误差逐渐变小。对于SPSO,在环境变化初期,由于峰值位置相对于初始位置变化较小,接近于静态环境下的位置,此时SPSO表现出较好的性能。随着迭代的持续进行,峰值位置相对初始阶段偏移较大,此时SPSO的跟踪性能呈现逐渐降低的趋势。从图1中还可以发现,在种群中引入一定量的新生个体,对算法维持较高的多样性有较大的帮助。在整个变化周期中,RIPSO的离线误差维持在一个较为稳定的水平,其原因是算法每一代都引入一定比例的新的随机产生的个体。

3.2 各变化强度下离线误差结果和分析

不同变化强度下各算法离线误差及其标准差见表2所列。

表2 不同变化强度下离线误差及其标准差

从表2可以得出,随着变化强度的增加,算法的离线误差相应地增加,整体的变化趋势与3.1节相似,即NSPSO在4个算法中最优,其次是RIPSO,再次是CPSO,最后是SPSO。进一步的分析可以看出,各算法虽然随着变化强度的增加离线误差也相应增加,但NSPSO在4个算法中离线误差增加最为缓慢,变化强度从0.5变化到6,NSPSO的离线误差从11.570增加到15.078,变化率约为30.3%。RIPSO、CPSO、SPSO算法的离线误差变化率依次为49.7%、60.5%、67.5%。NSPSO在不同变化强度下都有较强的追踪极值的能力,分析其原因是由于算法中把整个种群的粒子分为几类角色,不同角色采用不同的更新策略,使得种群中一部分个体(Leader个体和Follower个体)围绕当前最优解附近搜索的同时,还有一部分个体(Scouter个体)采用常规的更新策略在其他区域搜索。Scouter个体的搜索区域限制在其同类角色的范围内,一旦最优解移动到这些区域,则很快就被发现并被更新为Leader角色,同时个体围绕新的区域继续探寻最优解。因此在NSPSO中,即使最优解的位置经过多个演化代而偏离初始位置较大,NSPSO也能迅速地跟踪到其变化。当变化强度达到6时,其他算法已经很难跟踪到最优解,NSPSO由于粒子角色的动态更新,还能继续获得较低的离线误差。RIPSO由于每一代都引入一定新的个体,还能使算法获得较强的探索能力,其动态搜索性能仅次于NSPSO。SPSO则随着变化强度的增加,由于大多数粒子随着演化的进行而逐渐收敛到最优解附近,因而失去探索能力。

4 结 论

为了促使PSO在动态环境下有较好的性能,本文提出了基于NSPSO算法,通过对标准移动峰函数的实验,可以得出通过在PSO种群中引入多种角色,且不同角色执行不同的更新策略,使得算法在动态的环境下有较强的跟踪极值的能力。由于在演化过程中,不同粒子的更新策略不同,且粒子的角色也会根据其适应值的不同而不断变化,在不显著增加算法复杂性的前提下,使得算法能够较好地适应环境的变化。数值实验表明,即使在较强的变化强度下,其追踪极值的能力也能维持在较高的水平。通过多角色演化策略的引入,算法在不同的变化强度下均能维持探索能力和开采能力之间的平衡。

综上所述,本文提出的NSPSO算法在求解动态优化问题时具有良好的性能,且在变化强度较大的情况下也能维持较高的动态性能。下一步将研究算法在更复杂情形下的动态性能,以及不同角色比例对算法动态性能的影响。

[1] KENNEDY J,EBERHART R.Particle swarm optimization[C]//ICNN’95:Proceedings of the International Conference on Neural Networks.Piscataway:IEEE,1995:1942-1948.

[2] 杨兴明,许东昌,朱建,等.基于粒子群优化算法的两轮小车能量优化策略[J].合肥工业大学学报(自然科学版),2014,37(3):292-295,375.

[3] Peng X,Gao X,Yang S.Environment identification-based memory scheme for estimation of distribution algorithms in dynamic environments[J].Soft Computing,2010,15(2):311-326.

[4] Wu Y,Liu X X.Genetic algorithms with immigrants scheme for dynamic optimization problems[J].Applied Mechanics and Materials,2013,333/334/335:1379-1383.

[5] CHENG H.Dynamic genetic algorithms with hyper-mutation schemes for dynamic shortest path routing problem in mobile ad hoc networks[J].International Journal of Adaptive,Resilient and Autonomic Systems,2012,3(1):87-98.

[6] NABIZADEH S,REZVANIAN A,MEYBODI M R.A multi-swarm cellular PSO based on clonal selection algorithm in dynamic environments[C]//2012 International Conference on Informatics,Electronics & Vision (ICIEV).[S.l.]:IEEE,2012:482-486.

[7] 王洪峰,汪定伟.一种动态环境下带有记忆的三岛粒子群算法[J].系统工程学报,2008,23(2):252-256.

[8] SHARIFI A,KAZEMI KORDESTANI J,MAHDAVIANI M,et al.A novel hybrid adaptive collaborative approach based on particle swarm optimization and local search for dynamic optimization problems[J].Applied Soft Computing,2015,32:432-448.

[9] SHEN D,LI Y,SUN Y.Particle swarm optimization with neighborhood search for multimodal optimization problems[J].ICIC Express Letters,2012,6(8):2133-2140.

[10] HE S,WU Q H,SAUNDERS J R.Group search optimizer:an optimization algorithm inspired by animal searching behavior[J].IEEE Transactions on Evolutionary Computation,2009,13(5):973-990.

[11] BANHARNSAKUN A,ACHALAKUL T,SIRINAOVAKUL B.The best-so-far selection in Artificial Bee Colony algorithm[J].Applied Soft Computing,2011,11(2):2888-2901.

[12] BLACKWELL T.Dynamic search with charged swarms[C]//Proceedings of the Genetic and Evolutionary Computation Conference.San Francisco:Morgan Kaufmann Publishers Inc,2002:19-26.

[13] BRANKE J.The moving peaks benchmark website[EB/OL].[2015-09-02].http://www.aifb.uni-karlsruhe.de/～jbr/movpeaks.

[14] BLACKWELL T,BRANKE J.Multiswarms,exclusion,and anti-convergence in dynamic environments[J].IEEE Transactions on Evolutionary Computation,2006,10(4):459-472.

(责任编辑 马国锋)

Particle swarm optimization based on neighborhood search in dynamic environment

SHEN Dingcai1,2, HU Shengzhou1

(1.College of Mathematics and Computer Science, Gannan Normal University, Ganzhou 341000, China; 2.School of Computer and Information Science, Hubei Engineering University, Xiaogan 432000, China)

Canonical particle swarm optimization(PSO) loses its ability of tracking optimum in dynamic environment due to its convergence. In order to increase the diversity of the population to ensure the ability of tracking the changing optimum in dynamic environment, a neighborhood search particle swarm optimization(NSPSO) was proposed. The individuals in the population were sorted in descending order according to their fitness values at each step of the evolution, each individual was assigned one of the Leader, Follower, Scouter roles according to a preset proportion, and the individuals with different roles adopted different update strategies during the evolution, thus making the algorithm maintain a certain exploitation ability, at the same time keep a stronger exploration ability. The performance of the NSPSO algorithm was validated by a commonly used moving peak benchmark(MPB). Numerical results show that the NSPSO algorithm can effectively reduce the offline error, and the impact of environmental change intensity on offline error is less than that of other compared algorithms, thus verifying that the NSPSO algorithm can effectively track the changing optimum in dynamic environment.

particle swarm optimization(PSO); dynamic optimization problem; neighborhood search; multi-role; evolutionary computation

2015-09-22；

2016-01-11

湖北省教育厅科学技术研究资助项目(D20142703)

申鼎才(1975-),男,江西南康人,博士，赣南师范大学讲师.

10.3969/j.issn.1003-5060.2017.05.011

TP18

A

1003-5060(2017)05-0628-05