BP神经网络模糊PID控制器在DMF生产中的应用

王华强, 杨玉清

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

BP神经网络模糊PID控制器在DMF生产中的应用

王华强, 杨玉清

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

文章基于DMF在工业生产中的重要作用,对于其回收工艺中的精馏塔温度的控制,提出了BP神经网络模糊PID控制器的方案,并用遗传模拟退火算法对其进行优化。通过与传统PID控制器和模糊PID控制器的仿真结果比较可知,该方案更为实时有效,更加适用于工业生产。

DMF溶剂;温度控制;BP神经网络模糊PID;仿真;智能控制

DMF(二甲基甲酰胺)是一种在工业上常用的,能和水及大部分有机溶剂互溶的溶剂;也在湿法合成革的生产中,起着洗涤固化剂的重要作用。但是,该材料的强污染性使得在工业生产中要特别注意对其进行回收处理[1]。现阶段，大多数企业采用以下DMF回收处理过程:废液在二级浓缩塔完成初步浓缩后,进入精馏塔,当其质量分数达到99%时,再提取纯净DMF[2]。该系统的控制重点是精馏塔的温度控制子系统。

本文通过Matlab进行仿真,观察控制器对于精馏塔温度调节系统的控制效果,发现模糊神经网络和PID结合的控制器,解决了传统PID和模糊PID存在的问题。

1 系统结构

本系统的控制目的是保持塔内温度恒定,这里选用精馏塔的温度与导热油的流量来构成串级控制系统,如图1所示[3]。图1中,GC1为主控制器,通常采用PID控制规律;GC2为副控制器,通常采用P规律调节;y1为主变量温度;y2为副变量流量;GP2为副对象;GP1为主对象。精馏塔借助于导热油来保持塔内温度恒定,由于导热油的传热和精馏塔的传质过程,使控制对象的等效纯滞后时间很长。因此,实际的工业过程不能单纯采用一阶过程来描述,而是用纯滞后项加一阶模型来描述。

图1 串级控制系统结构

对于副控对象-导热油的流量,假设控制通道的动态特性[4]可表示为:

(1)

其中,流量滞后时间常数T2≥0，且基本不变；导热油流速系数K2通常在一定范围内变化。假设K2=0.005～0.20 t/h,T2=0.6 min=36 s。

对于主控对象-温度,假设控制通道的动态特性可以表示为:

(2)

并假设温度变化系数KP1=3～10 ℃·(t/h)-1,温度变化滞后时间常数TP1=3～6 min,TP2=0～2 min,系统纯滞后时间常数τP=2～5 min。

在本文研究的精馏塔系统中,以上参数分别取值为:K2=0.20 t/h,KP1=3 ℃·(t/h)-1,TP1=3 min=180 s,TP2=0 min,τP=5 min=300 s。将参数取值代入(1)式、(2)式中,有

通常采用P控制规律就可以满足副控制器GC2,因此不做改变;而对于通常采用传统PID控制规律的主控制器GC1加以改进。改进后的BP神经网络模糊PID控制原理如图2所示。

图2 BP神经网络模糊PID控制原理

图2中包括经典PID控制器模块、模糊化模块和神经网络模块[5]。神经网络模块通过自身权系数的调整,实现对参数KP、KI和KD的调整,从而输送到PID控制器,实现对被控对象的控制作用。

2 BP神经网络模糊PID控制器

2.1 PID控制器模块

采用改进的积分分离PID算法,即

(3)

其中,KP、KI和KD分别为比例、积分和微分系数;u(k)为2次采样时刻的导热油阀门开度的变化量;e(k)为第k次的输入偏差;r(k)为给定的理想输出量。(3)式中,当e(k)小于等于预定的阈值A时，KL=1,即引入积分作用;当e(k)大于预定阈值A时,KL=0,即取消积分作用。PID控制主要是通过对KP、KI和KD3个系数的调节,来达到它的控制目的。

2.2 模糊化模块

模糊化模块是用于对系统的偏差e(k)、偏差变化率Δe(k)、KP、KI和KD进行模糊化处理,具有鲁棒性和非线性控制作用。基于对导热油阀门开度的控制,以上变量均可分为7个等级:正大、正中、正小、适中、负小、负中和负大,分别用PB、PM、PS、ZE、NS、NM和NB表示。结合大量操作工实际调节的经验,建立KP、KI、KD与e(k)、Δe(k)之间的模糊控制规则表,见表1所列。

输入量经过模糊化处理后得到模糊化的输出值,再传送给神经网络,实现了网络的模糊映射。

表1 模糊控制规则

2.3 神经网络模块

神经网络是一种具有并行计算、分布式信息存储、容错能力强和自适应学习功能的控制系统。但是BP神经网络易于陷入局部极小值,收敛速度慢,且易引起震荡,本文采用遗传模拟退火(geneticsimulatedanncaling,GSA)算法来对其进行优化。在对基于GSA算法优化的BP神经网络的设计上,主要分为BP神经网络结构的确定和GSA中的权值和阈值的选定[6]。

2.3.1BP神经网络结构的确定

模糊BP神经网络的结构如图3所示[7]。神经网络的第1层为输入层,直接把输入量传递到下一层；第2层为模糊子集层,选用钟型函数作为隶属度函数,完成模糊化运算[8]的任务,把输入量转化为模糊量；第3层为模糊规则层,完成模糊推理过程,并加以归一化处理；第4层为输出层,清晰化处理并输出3个参数。

图3 模糊BP神经网络结构

第1层～第4层的神经元节点的输入输出关系如下:

其中，i=1,2;j=1,2,…,7;k=1,2,…,n；mij和σij分别为隶属度函数的中心值和宽度。

其中,wij为网络第3层～第4层的权值。

2.3.2GSA算法中权值和阈值的选定

遗传模拟退火算法的步骤[9]如下：

(1) 染色体编码,确定初始种群、进化代数、初始温度T0和退火速率等参数。

(2) 确定适应度函数,并评价个体适应度。采用适应度拉伸方法,第i个个体改进后适应度为:

其中,t为当前温度,t=T0(0.99g-1);g为当前遗传进化代数;φi为改进前第i个个体适应度;m为种群规模;s为输出层节点数目;Tj为网络的期望输出;Aj为网络的实际输出。

(3) 进行遗传模拟退火操作，即选择、交叉、变异、退火。

在数量为m的种群里,采用轮盘赌转法从当代种群中选取个体i1和i2,则在新种群中选择接受i1的概率为:

其中,t为当前退火温度。

交叉概率Pc和变异概率Pm由个体适应度来确定，具体计算公式如下:

引入最优保留策略,对群体中每个个体进行退火操作。

(4) 判断是否满足终止条件,若满足则终止,否则,返回步骤(2)。

(5) 保存和解码最优个体,返回给BP。

2.4 控制算法的实现

BP神经网络模糊PID控制算法的实现步骤[10]如下:

(1) 确定BP神经网络结构。

(2) 利用遗传模拟退火算法选定参数wij、mij和σij的最优初值,并选定学习速率β,迭代次数k=1。

(3) 由采样得到r(k)和y(k)的值,通过e(k)=r(k)-y(k)计算出e(k)。

(4)e(k)和Δe(k)作为神经网络的输入。

(5) 计算得出神经网络每一层的输入和输出,输出层的输出是PID控制器的3个可调参数KP、KI、KD。

(6) 计算出PID控制器输出的控制量u(k),在线调整参数wij、mij和σij。

(7) 置k=k+1,然后返回步骤(3)。

BP神经网络在线学习的性能指标函数为:

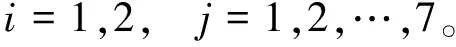
其中,β为学习速率,β>0。

3 控制器仿真实验

在Matlab软件的Simulink环境下进行传统PID和模糊PID控制器的仿真。对精馏塔模型中得到的传递函数0.2/(36S+1)和3e-300S/(180S+1),采用试凑法调节PID系数KP=0.8,KI=0.003 2,KD=10;设置e和Δe模糊论域为[-3，3];KP、KI和KD论域均为[0，1];用Mamdani法根据表1设置模糊规则;设置参数Ke=0.01,Kec=0.01，K3=0.1,KP0=0.8，KD0=10,KI0=0.003 2,K1=0.000 1,K2=0.000 1;并且调节反应时间长度和步长的大小,得到的仿真曲线如图4所示。

BP神经网络模糊PID控制器的仿真[11-12]是通过在Matlab中进行编程,设定最大训练次数为200次,训练的目标误差设置为0.001,然后对BP神经网络开始训练,直到满足所设条件。仿真结果如图5所示。

图4 传统PID、模糊PID仿真曲线

图5 BP神经网络模糊PID仿真曲线

通过比较3种控制器的仿真曲线,可以得到3种控制方式的性能指标参数,见表2所列。

表2 控制器性能指标

4 结 论

通过本文分析可知，BP神经网络模糊PID控制器的性能比传统PID和模糊PID控制器更加优良,经过GSA算法的优化,加快了BP神经网络的收敛速率,提高了系统的智能化水平。该控制系统具有稳定、快速以及自适应能力强、鲁棒性好等优点,现已应用于某企业的DMF工业生产中,控制效果比以前有明显的改善。

[1] 孙一新,李宏光.DMF回收精馏塔开车过程控制任务的Petri网建模及分析[J].化工自动化及仪表，2008，35(5):27-32.

[2] 赵舜华，宋锡瑾,裴宁,等.聚氨酯合成革湿法生产废气中DMF的回收工艺[J].中国化学工程学报,2008，16(3):461-464.

[3] 俞金寿，顾幸生.过程控制工程[M].北京:高等教育出版社，2012:198-240.

[4] 陈夕松.过程控制工程[M].北京:科学出版社，2005:173-189.

[5] 王华强,石亚娟,王健波.神经模糊网络PID在水轮机调速系统中的应用[J].合肥工业大学学报(自然科学版)，2012，35(9):1187-1191.

[6] HART E，TIMMIS J.Application areas of AIS: the past，the present and the future[J].Applied Soft Computing，2008，8(1):191-201.

[7] 葛锁良,方唐利,岳胜.采用免疫BP算法的模糊神经网络PID控制器[J].合肥工业大学学报(自然科学版)，2011，34(5):679-682，704.

[8] 张咏军,王航宇.基于BP神经网络的温度模糊PID控制器设计[J].现代电子技术，2008(7):133-135.

[9] 杜宗宗，刘国栋.基于混合遗传模拟退火算法求解TSP问题[J].计算机工程与应用，2010，29(2):179-183.

[10] 陈政文.基于模糊PID控制的退火炉温度控制系统的研究[D].武汉:武汉工程大学，2014.

[11] LI M，SETHI I K.Confidence-based active learning[J].IEEE Transaction on Pattern Analysis and Machine Intelligence，2005，28(8):1251-1261.

[12] 周开利,康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京:清华大学出版社，2005:1-255.

(责任编辑 张 镅)

Application of BP neural network fuzzy PID controller in DMF industrial production

WANG Huaqiang, YANG Yuqing

(School of Electric Engineering and Automation， Hefei University of Technology， Hefei 230009， China)

Based on the important role of DMF in industrial production， this paper presents the BP neural network fuzzy PID controller solutions for controlling the temperature of the fractionator used in recovery process. And the BP neural network is optimized by using the genetic simulated annealing algorithm. The simulation results are compared to those of the traditional PID controller and fuzzy PID controller， and it is shown that the presented controller is more effective and more suitable for industrial production.

DMF solvent; temperature control; BP neural network fuzzy PID; simulation; intelligent control

2015-12-16；

2016-03-18

合肥工业大学产学研校企合作资助项目(12-069；13-214)

王华强(1963-),男,安徽合肥人,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.05.015

TP273.4

A

1003-5060(2017)05-0649-04