共形空间中的Blaschke全脐子流形

章左,聂昌雄

(湖北大学数学与统计学学院，湖北 武汉 430062)



共形空间中的Blaschke全脐子流形

章左,聂昌雄

(湖北大学数学与统计学学院，湖北 武汉 430062)

在共形群下的完全不变量体系下讨论4种共形不变量之间的关系，并在共形等价意义下分类一些特殊子流形.

共形空间；共形不变量；常数量曲率；Blaschke全脐子流形；Blaschke拟全脐子流形

0 引言

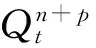
1 基本公式

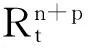
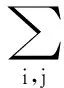
由结构方程

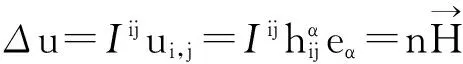
(1)

(2)

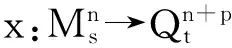
对

存在整体提升

故

由

知

(3)

令

p=(1,0,1),yi=(0,ui,0)+(ui,u)p,ζα=(0,eα,0)+〈eα,u〉p.

由

1=〈N,Y〉, 0=〈-N,Yi〉, 0=〈-eτN,ξ〉, 0=〈-eτN,-eτN〉,

可以得到

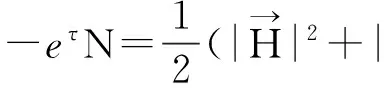
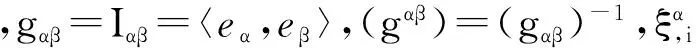
易算出

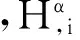
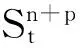
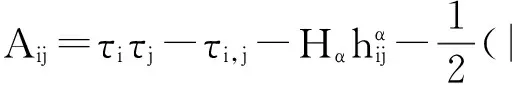
(4)

(5)

(6)

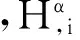
2 共形空间中的Blaschke全脐子流形

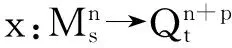
命题2.1的证明 因为

由带常数量曲率的极小正则子流形的性质知ρI=常数,Hα=0.

由(4)和(6)式知τ=常数,有

不妨令

有

A=λg,Φ=0.

命题2.2 若x=σ∘u是Blaschke全脐子流形,则λ=常数.

因为{Y1,…,Yn}线性无关,所以

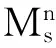
定理2.1 若x=σ∘u是Blaschke全脐子流形,则x共形等价于带常数量曲率的极小正则子流形.

定理2.1的证明 对A=λg两边取迹,由tr(A)=nλ,易知

从而ρ=常数.

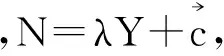
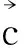
下面分3种情况考虑：

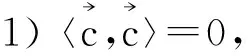
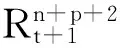
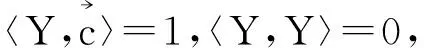
I=(du,du)=(dY,dY)=g,

推出

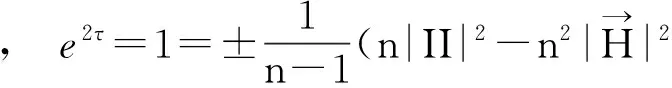
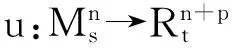
由

知

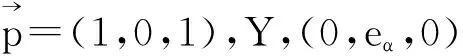
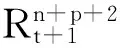
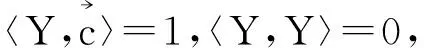
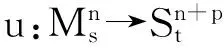
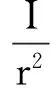
得

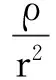
由

知

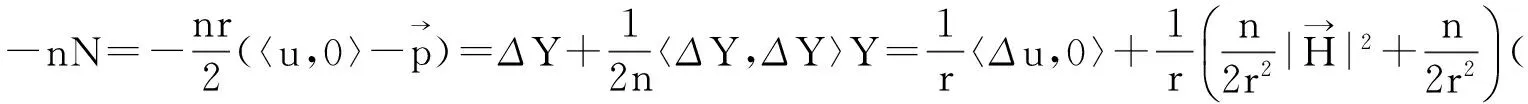
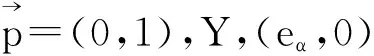
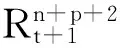
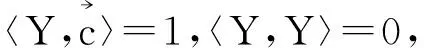
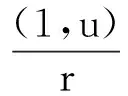
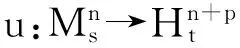
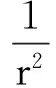
得

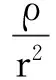
由

知

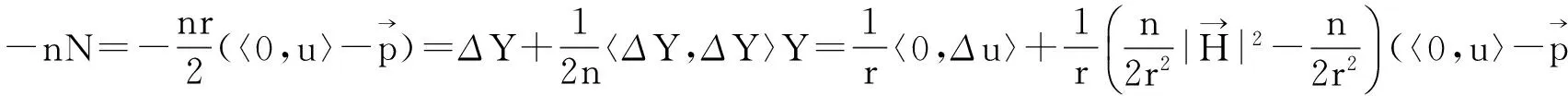
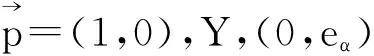
3 共形空间中的Blaschke拟全脐子流形

A=λg+〈B,ξ〉,Φ=0

(7)

所以e2τ=常数.由(4)式和(6)式知τ=常数,有

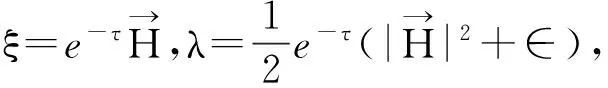
命题3.2 假设x=σ∘u是一个Blaschke拟全脐子流形,则λ一定是常数.

因为{Y1,…,Yn}线性无关,所以

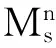
λ=常数.

定理3.1 若x=σ∘u是Blaschke拟全脐子流形,则x共形等价于带常数量曲率和平行平均曲率向量场的正则子流形.

定理3.1的证明 对(7)的第一个式子取迹知

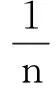
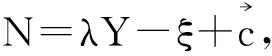
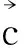
下面分3种情况考虑：

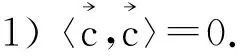
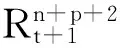
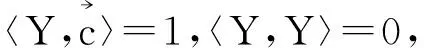
I=(du,du)=(dY,dY)=g,

推出

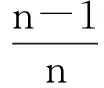
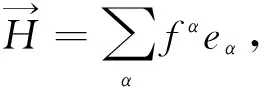
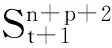
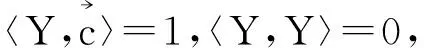
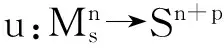
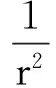
得

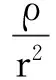
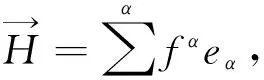
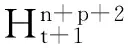
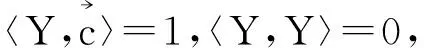
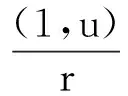
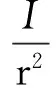
得

[1] Chen S S, do Carmo M, Kobayashi S. Minimal submanifolds of a sphere with second fundamental from of constant lenghth [J]. Berlin:Springer 1970:56-79.

[2] Yau S T, Submanifolds with constant mcan curvature[J].Amer J Math, 1974, 96:342-370.

[3] Li H Z, Liu H L, Wang C P, et al. Moebius isoparametric hypersurfaces in with two distinct principal curvatures [J] Acta Math Sinica (Engl Ser) 2002,18:437-446.

[4] Wang C P. Surfaces in Möbius geometry[J]. Nagoya Math J, 1992 125:53-72.

[5] Wang C P. Möbius geometry of submanifolds inSn[J]. Manuscripta Math,1998 96:517-534.

[6] Li H Z, Wang C P. Surfaces with vanishing Moebius form inSn[J]. Acta Math,Sinica (Engl Ser), 2003,19:671-678.

[7] Brasila A, Chavesb R M B, Mariano M，et al. Complete spacelike submanifolds with parallel mean curvature vector in a semi-Riemannian space form[J].J Geom Phys, 2006, 56：2177-2188.

[9] Nie C X, Wu C X. Classification of type I time-like hyperspaces with parallel conformal second fundamental forms in the conformal space[J].Acta Math Sinica 2011 54(1)：685-692.

[10] 聂昌雄,吴传喜.共形空间中的正则子流形[J]. 数学年刊 2008,29A(3):315-324.

[11] 郭震.关于常曲率空间中具平行平均曲率向量的子流形[J]. 云南师范大学学报(自然科学版) 1992(4)：1-9.

[12] 张廷枋.Sn中Moebius形式平行的曲面[J]. 数学研究, 2003, 36(3):235-242.

[13] 张廷枋,钟定兴.Sn中Moebius形式为零的曲面[J]. 数学学报, 2004, 47：241-250.

[14] 伍鸿熙,沈纯理,虞言林.黎曼几何初步[M]. 北京：北京大学出版社 1988.

[15] 陈维桓,李兴校.黎曼几何引论(上册)[M]. 北京：北京大学出版社 2002.

(责任编辑 赵燕)

Blaschke umbilical submanifolds in the conformal space

ZHANG Zuo，NIE Changxiong

(Faculty of Mathematics and Statistics, Hubei University，Wuhan 430062，China)

Since professor changping wang has established the conformal differential geometry theory of submanifolds based on the nature of the conformal differential geometry and submanifolds are obtained under the conformal group fully invariant system.Conformal differential geometry research made greater progress.In this case,we discussed the relationship between the four kinds of conformal invariant,we classified some kinds of special submanifolds under the conformal equivalence.

conformal space；conformal invariant；constant scalar curvature；Blaschke umbilical submanifolds；Blaschke quasi-umbilical submanifolds

2016-12-14

国家自然科学基金(11571037)资助

章左(1990-) 女 硕士生; 聂昌雄，通信作者，副教授.E-mail:nie.hubu@yahoo.com.cn

1000-2375(2017)04-0417-06

O186.1

A

10.3969/j.issn.1000-2375.2017.04.015