基于RBF神经网络与NSGA-Ⅱ算法的渣浆泵多目标参数优化

王春林，冯一鸣，叶 剑，罗 波，刘轲轲

（江苏大学能源与动力工程学院，镇江 212013）

基于RBF神经网络与NSGA-Ⅱ算法的渣浆泵多目标参数优化

王春林，冯一鸣，叶 剑，罗 波，刘轲轲

（江苏大学能源与动力工程学院，镇江 212013）

由于渣浆泵普遍存在扬程低于设计扬程、效率低、磨损严重等问题，该文选取比转速为75的离心式渣浆泵为研究对象，运用商用CFD求解软件Flunet，选取RNGk-ε湍流模型与欧拉两相流模型对其内部流动进行计算。以离心式渣浆泵的效率、高效区作为优化目标，结合Plackeet-Burman筛选试验，将渣浆泵叶片的进口安放角、出口安放角与叶片包角作为优化变量。采用均匀试验设计安排样本空间，利用 RBF神经网络拟合优化变量与优化目标间的映射关联，基于NSGA-Ⅱ遗传算法进行多目标寻优。针对优化所得的Pareto解集，选取其中效率最优个体和高效区最优个体与优化前初始模型进行对比：分析了上述3个个体的通过数值模拟得到的性能曲线之间的差异，得到效率最优与叶片进、出口安放角、叶片包角为21.76°、23.43°、145.56°，高效区最优时为19.38°、22.68°、116.71°。通过试验验证，优化后个体性能得到显著提升，效率最优个体的效率较初始个体的效率提高了3.81%，高效区最优个体较初始个体高效区范围提高了4.33%。给出并分析了上述3个个体在叶轮流道中间剖面上固相相对速度矢量及湍动能分布、叶片工作面、叶轮后盖板的固相浓度分布差异。优化结果表明，该优化方法使叶轮的水力特性得到改善，提高了离心式渣浆泵的性能。

泵；数值模拟；优化；RBF神经网络；NSGA-Ⅱ遗传算法；多目标优化

王春林，冯一鸣，叶 剑，罗 波，刘轲轲. 基于RBF神经网络与NSGA-Ⅱ算法的渣浆泵多目标参数优化[J]. 农业工程学报，2017，33(10)：109－115. doi：10.11975/j.issn.1002-6819.2017.10.014 http://www.tcsae.org

Wang Chunlin, Feng Yiming, Ye Jian, Luo Bo, Liu Keke. Multi-objective parameters optimization of centrifugal slurry pump based on RBF neural network and NSGA-Ⅱ genetic algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(10): 109－115. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.10.014 http://www.tcsae.org

0 引 言

由于渣浆泵输送的是固液两相介质，泵内流体的流动状态与清水泵相差甚远，其设计也更为复杂，设计要求也高于普通的单相流泵，且目前尚无统一的设计准则。国内外学者对离心式渣浆泵的研究付出了艰辛的努力，大体上经历了从单纯试验研究到试验与CFD数值模拟相结合研究的阶段。由于设计理论的缺乏与数学模型的尚不完善，早期对渣浆泵的研究均是采用试验的方法[1-3]。

随着计算机硬件与软件的不断更新，计算流体力学（computational fluid dynamics）的发展也日新月异。由于计算机仿真具有试验成本低、设计周期短、模拟结果可靠等特点，已成为诸多研究者用来研究流体机械的首选手段[4-6]。

由于两相流体的流动规律较单相流动更为复杂，渣浆泵的设计理论不能照搬清水泵的设计理论，否则将无法满足设计的要求。许多专家学者经过多年的研究探索，提出了一些对渣浆泵的设计具有指导意义的理论或方法[7-10]。对于描述固液两相流动的模型，需要根据特定的情况来选取。随着实际生产过程的高速化与智能化，对设备的各方面性能均提出了更高的要求。而装备性能提升的问题，大多数情况下是属于优化的范畴，不仅仅只局限于某一方面，因此可以将这些问题归纳为多目标的优化问题。

近年来，迅速发展与改进的智能优化算法在流体机械领域也得到了广泛应用，并取得了丰硕成果[11-14]。虽然智能优化算法逐渐被广泛地应用与流体机械的优化设计，但目前的研究一般仅考虑了流体机械运输的介质为单相介质的情形。将智能优化算法用于对渣浆泵的优化设计却罕见报道。因此，本课题采用RBF(radial basis function)神经网络拟合离心式渣浆泵的结构参数与性能指标之间的映射关系作为响应模型，利用NSGA-Ⅱ遗传算法在样本空间内进行全局寻优。通过优化离心式渣浆泵的结构参数来达到提高其性能的目的，为离心式渣浆泵的优化设计提供新的思路。

1 渣浆泵数值计算

1.1 渣浆泵的两相流基本方程式

在工作原理上，离心式渣浆泵与普通的清水离心泵是相同的。由于渣浆泵抽送的是固液两相介质，与清水单相介质的物理化学特性差异较大，用清水泵的设计理论来设计渣浆泵，其实质就是把固液两相流体作为单相流体流动模型来考虑。由于泵内固液两相始终存在不同的速度场，采用单相流体流动模型设计的泵的叶型和流道不能适应能量最有效的转换，使流道内流动状态恶化，造成泵的效率低，使用寿命短，运行噪声大，振动大。

建立如式（1）的离心式渣浆泵的基本方程式[15]，该方程式是渣浆泵固液流设计的理论依据，这和清水泵的单相流设计理论既有一定的联系，又有着本质的区别，以该基本方程式为理论基础设计的离心式渣浆泵，有利于提高渣浆泵的效率、通过性、抗磨性、输送性、汽蚀性[16-19]，以及延长泵的使用寿命、降低运行噪声与振动等，是提高渣浆泵性能的根本途径。

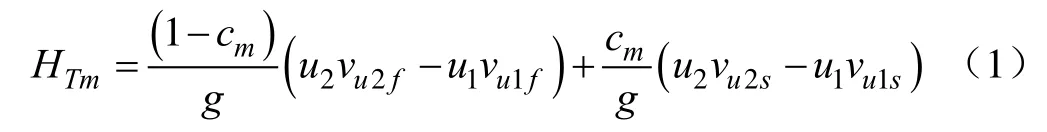
式中HTm为泵的理论扬程，m；cm为固液两相流体的质量浓度；u1、u2为叶轮进、出口液相圆周速度，m/s；vu1f、vu2f为叶轮进、出口液相绝对速度的圆周分量，m/s；vu1s、vu2s为叶轮进、出口固相绝对速度的圆周分量，m/s。

1.2 高效区定义

高效区是指泵运行时的高效工作区，一般用流量的相对宽度HE表示，其定义的表达式如下：

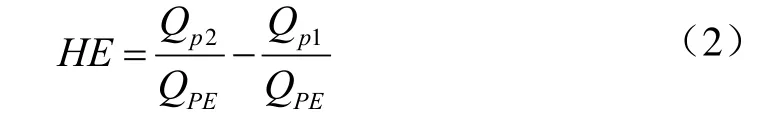
式中QPE为效率为峰值hPE时的流量，m3/s；QP1，QP2为效率为0.95hPE时的流量，m3/s。

1.3 计算模型及网格划分

本文以某一离心式渣浆泵作为初始模型，其设计参数为：流量Q=95 m3/h，扬程H=26 m，转速n=1 450 r/min，效率η=69.02%，比转速ns=75；其几何参数为：叶轮进口直径：Dj=80 mm，叶轮出口直径：D2=150 mm，叶轮进口安放角：b1=21°，叶轮出口安放角：b2=31°，叶片包角： =130°，水泵进口延长段长度尺寸：320 mm,水泵出口延长段尺寸：400 mm。

模型计算域包括叶轮流道与蜗壳流道。为让进出口的湍流充分发展，将水泵进口段和出口段均延长一定长度进行计算，如图 1所示。其中进口段与出口段采用结构网格，而叶轮与蜗壳采用非结构网格（图2）。

图1 初始模型的计算域Fig.1 Calculation area of initial model pump

表1展示了本文选取的用于网格无关性验证的5组网格数目。计算工况为：流量Q=95 m3/h，固液两相介质的进口速度v=5.279 89 m/s，叶轮转速n=1 450 r/min，初始固相体积分数Cv=0.2，颗粒粒径ds=1.0 mm，颗粒密度ρ=2 000 kg/m3。

通过Fluent计算与比较。尽管Mesh 3～Mesh 5的网格致密度高，但Mesh 2已经满足计算要求，考虑到计算的时间成本，选用Mesh 2。

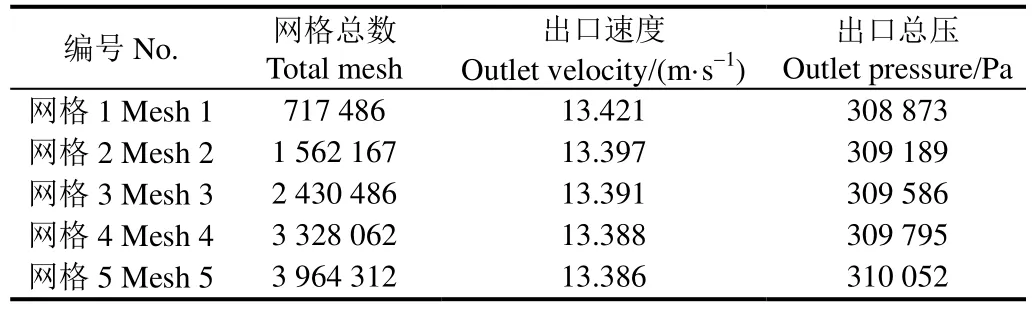
表1 网格无关性验证Table 1 Grid independence verification

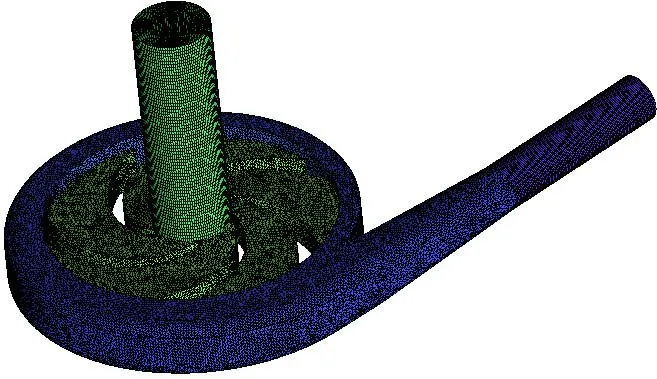
图2 初始模型的计算域网格示意图Fig.2 Calculation grid diagram of initial model pump

1.4 边界条件

采用RNGk-ε湍流模型与欧拉两相流模型，速度进口，自由出流，壁面上满足无滑移固壁条件，近壁区域采用湍流模型自带的壁面函数，动静结合面采用 frozen rotor interface进行处理。

1.5 外特性验证

为验证数值计算结果的可信性，对所研究的模型泵进行性能试验。试验在江苏大学流体机械试验室C级闭式性能试验台上进行。流量测量采用HLD型电磁流量计，测量精度为±0.30%，扬程测量采用WT-1151型智能电容式压力变送器，测量精度为±0.25%，功率、转速测量选用JN338-100AG型转矩转速仪，转速测量精度为±0.05%。

本试验系统运行稳定，重复性好，其效率综合误差为±0.836%，试验方法按照GB/T3216-2005《回转动力泵水力性能验收试验1级和2级》试验方法的规范进行。

图 3为数值计算得到的性能曲线与试验得到的性能曲线对比图。整体上，数值模拟得到的性能曲线优于试验得到的性能曲线，这是由于数值模拟过程中，将泵内流体的流动和泵的结构做了适当简化和假设。在整个流量范围内，两者的吻合程度较高。因此，可以认为数值模拟能够真实地反映各工况条件下的性能。

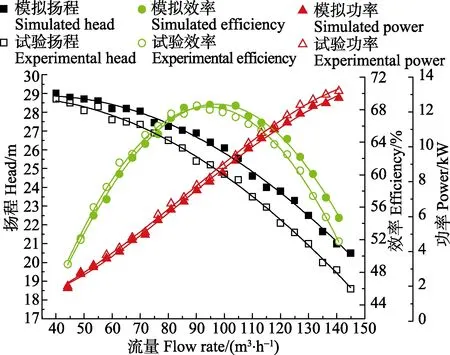
图3 初始模型的外特性曲线的计算值与试验值对比Fig.3 Comparison of initial model external characteristic curves between calculation value and experiment value

2 多目标寻优

2.1 参数筛选

王哲，洑颢，梁照恒，等.基于PS@Ag纳米探针和Si@Ag阵列基底的SERS特性的肿瘤标志物免疫检测[J].光子学报，2018，47(12)：1228002

为明确显著影响离心式渣浆泵性能的几何参数，避免浪费试验资源，本文基于Design Expert 8.0.5b软件对渣浆泵的主要几何参数进行Plackett-Burman试验设计，如表2所示选取描述离心式渣浆泵结构的12个几何参数进行筛选，另外增设 2组水平，其值分别为模型泵相关几何参数的1.2倍和0.8倍，试验共进行20次。利用CFD软件Fluent获得20组相应的最高效率和高效区数据，而结果分析由软件Design Expert8.0.5b完成。

分析结果显示显著因素为进口安放角β1、出口安放角β2、叶片包角φ。故本文选取这3个几何参数作为下一步优化设计的优化变量。

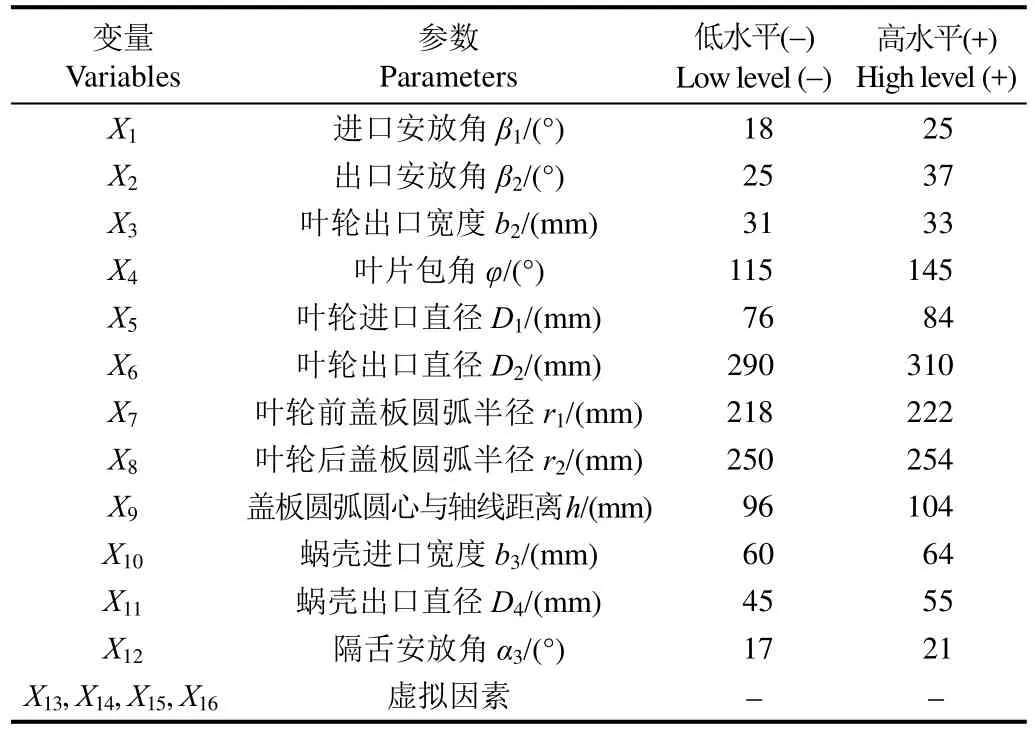
表2 Plackett-Burman设计因素及其水平Table 2 Range of different factors investigated with Plackett-Burman

2.2 试验安排

考虑到训练及测试RBF神经网络所需要的样本点数据的规模，本文进行3因素、37水平均匀试验来建立训练及测试所需的样本。使用均匀表U37(3712)设计均匀试验，试验表设计与模拟结果如表3所示。

2.3 RBF神经网络

离心式渣浆泵的性能指标最高效率、高效区与结构参数之间的关系是未知的复杂的非线性关系，根据目前的研究，暂时还无法用合适的数学模型来表达。因此，需要建立一个神经网络来表达拟合自变量与优化目标之间的映射关系[19-23]。本文通过RBF神经网络拟合出渣浆泵结构参数与其最高效率、高效区的数学关系。图 4为RBF神经网络结构示意图，在本文中所选取的3个几何参数：进口安放角，出口安放角和叶片包角作为 3维输入向量，最高效率和高效区则为输出向量，输入输出向量已由表3给出，qi则是二者间数学关系，为未知，但可以通过训练RBF神经网络拟合出来。

其中第i个隐层节点输出：

式中x为n维输入向量；y为输出向量；ci为第i个隐层节点的中心，维数为n；||·||为欧几里得范数；Φ(·)为径向基函数。

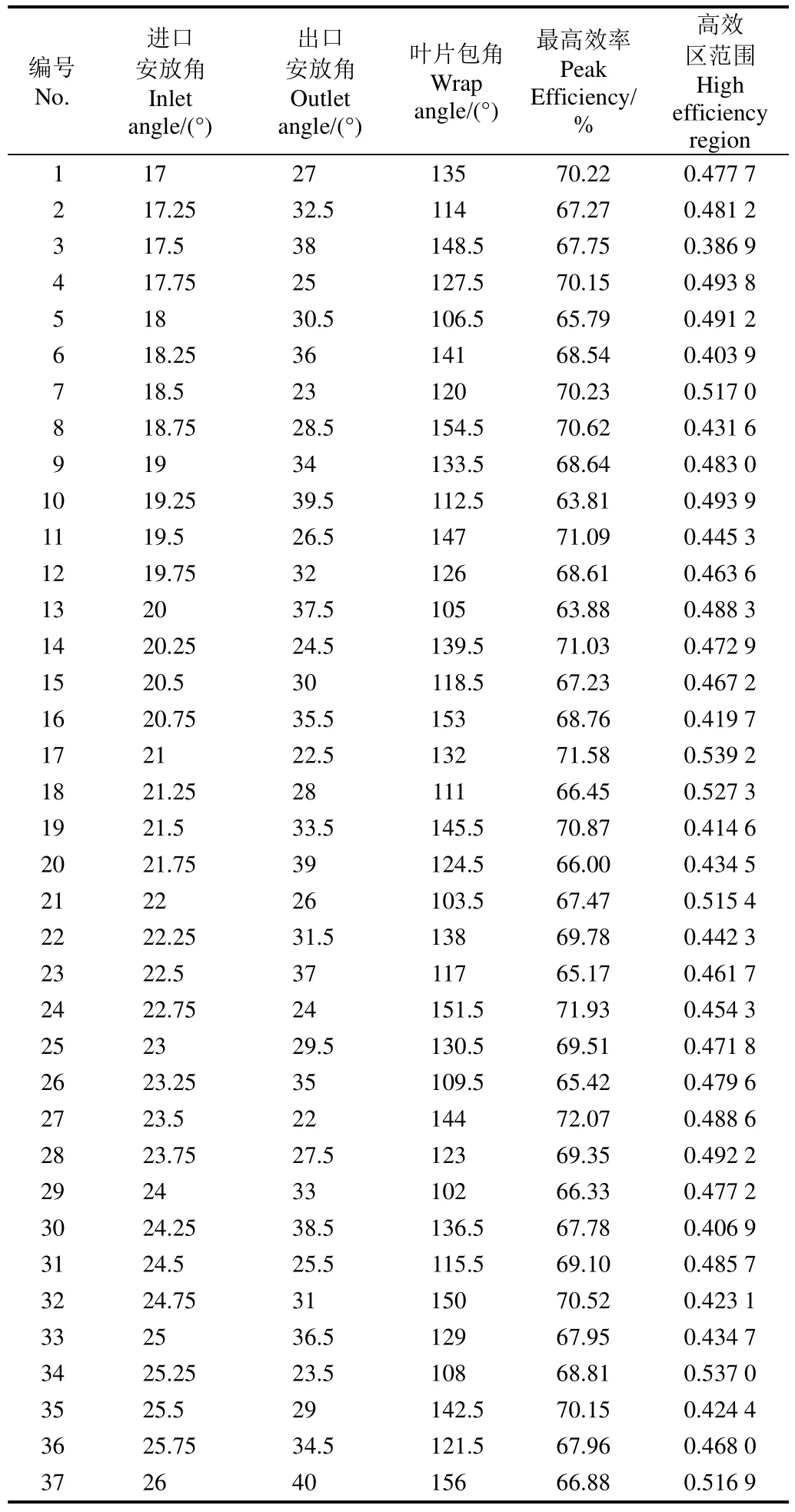
表3 均匀试验设计及模拟结果Table 3 Uniform experiment design and simulation results

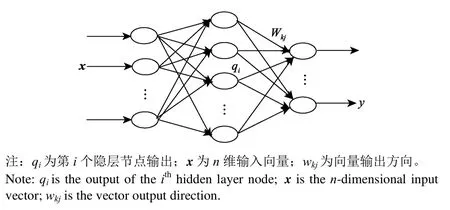
图4 RBF神经网络结构示意图Fig.4 Structure diagram of RBF neural network

带精英策略的快速非支配排序遗传算法[24-27]（NSGA-Ⅱ），提出了快速非支配排序算法，降低了计算的复杂度，使算法的复杂度由原来的O(MN3)下降到O(MN2)；引入精英策略（Elitist），扩大采样空间。将父代种群与其产生的子代种群组合，共同竞争产生下一代种群，有利于保持父代中的优良个体进入下一代，保证某些优良的种群个体在进化过程中不会被丢弃，从而提高了优化结果的精度。并通过对种群中所有个体的分层存放，使得最佳个体不会丢失，迅速提高种群水平；采用拥挤度和拥挤度比较算子，不但克服了NSGA中需要人为指定共享参数的缺陷，而且将其作为种群中个体间的比较标准，使得准Pareto域中的个体能均匀地扩展到整个Pareto域，保证了种群的多样性[27-30]。训练并测试完成的RBF神经网络是无法用数学解析式的方法表达，而NSGA-Ⅱ遗传算法可以将RBF神经网络作为适应度值的响应模型，展开对 RBF神经网络的输出向量以及输入向量的寻优计算，即是对离心式渣浆泵的最高效率、高效区和其对应的进出口安放角和包角值的寻优计算。

3 结果分析

3.1 优化结果基本分析

本文中采用交叉概率为 0.9，选取初始种群规模为100，经过500次遗传迭代进行全局寻优。

多目标遗传算法NSGA-Ⅱ经过500代迭代寻优后，得到了相应的非支配解集。如图 5所示，为经过遗传算法优化之后得到的 Pareto最优前沿。可以观察到，经过优化后得到的 Pareto最优解，密集、连续且光滑地沿一条整体上呈上凸形的曲线分布，这表明NSGA-Ⅱ在样本空间内具有很强的逼近Pareto解的能力。表4为最优前沿中位于前5的Pareto解，效率最大值为73.79%，与此对应的高效区为0.487 6；高效区最大值为0.551 8，而与此对应的最高效率为69.19%。

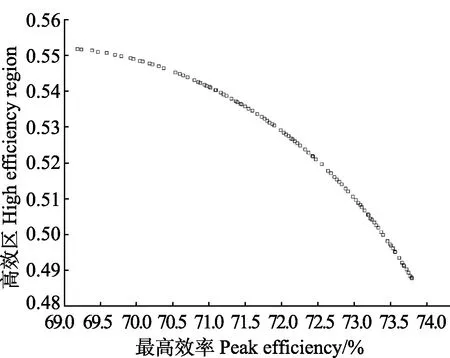
图5 优化后的Pareto前沿分布Fig.5 Distribution of the Pareto frontier after optimization

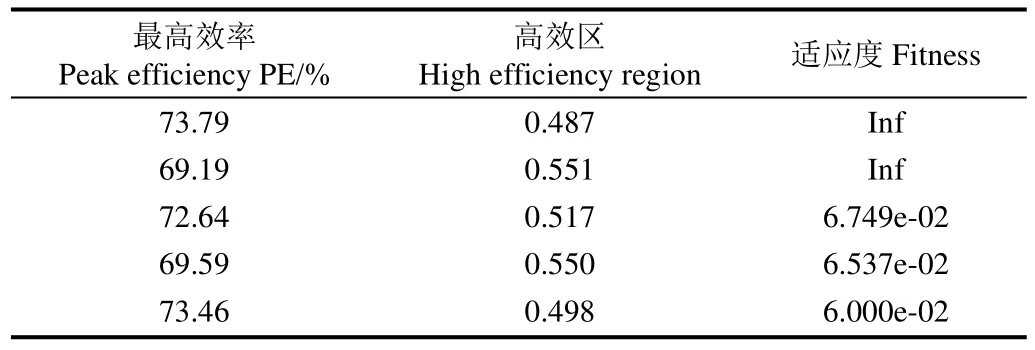
表4 最优前沿中位于前5的Pareto解Table 4 Top 5 solutions of Pareto front

根据优化后的 Pareto解集文件，得到效率最优个体对应的进口安放角、出口安放角、叶片包角，为β1=21.76°，β2=23.43°，φ=145.56°；高效区最优个体对应的进口安放角、出口安放角、叶片包角，将数据进行反归一化处理后，为β1=19.38°，β2=22.68°，φ=116.71°。

根据上述 2个极值解对应的参数，确定相应的离心式渣浆泵叶轮，然后再分别对相应的泵进行试验验证。效率最优个体的β2较初始个体有所减小，β1、φ则较初始个体有所增大，而高效区最优个体的进口安放角β1、出口安放角β2、叶片包角φ的大小较初始个体均有所减小。图6为经NSGA-Ⅱ遗传算法优化前后的叶轮三维对比图。

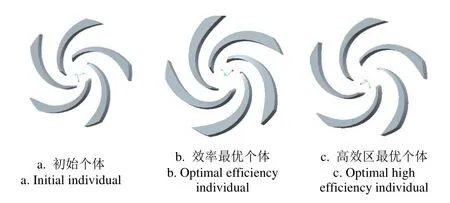
图6 NSGA-Ⅱ遗传算法优化前后的叶轮三维对比图Fig.6 Comparison of 3D models of initial impeller and optimal impeller by NSGA-Ⅱ

3.2 优化前后外特性对比分析

图 7为初始模型泵的试验外特性曲线与效率最优个体以及高效区最优个体的试验外特性曲线对比图。初始个体在流量Q=93.56 m3/h时到达最大效率68.62%，高效区范围为0.495 5。

效率最优个体在流量Q=91.88 m3/h时到达最大效率72.43%，高效区范围为0.476 4，其效率最优工况较初始个体往小流量区偏移1.68 m3/h，最高效率比初始个体提高3.81个百分点，但高效区范围比初始个体减小0.019 1，减小的幅度为3.85%。效率最优个体与初始个体的试验效率曲线，直观上可以看到前者的效率曲线尖而窄，而后者是效率曲线则相对平缓。

高效区最优个体在流量Q=88.71 m3/h时到达最大效率68.69%，高效区范围为0.517，高效区范围比初始个体增加0.021 5，增加的幅度为4.33%。高效区最优个体与初始个体的试验效率曲线，直观上可以看到优化后个体在小流量工况下效率更高、高效区范围更广。

3.3 优化前后流场对比分析

本文选取优化后的效率最优个体及高效区最优个体的流场与初始线性分布个体流场展开对比分析。图 8和图 9分别为叶轮流道在中间剖面上固相相对速度矢量与湍动能分布。

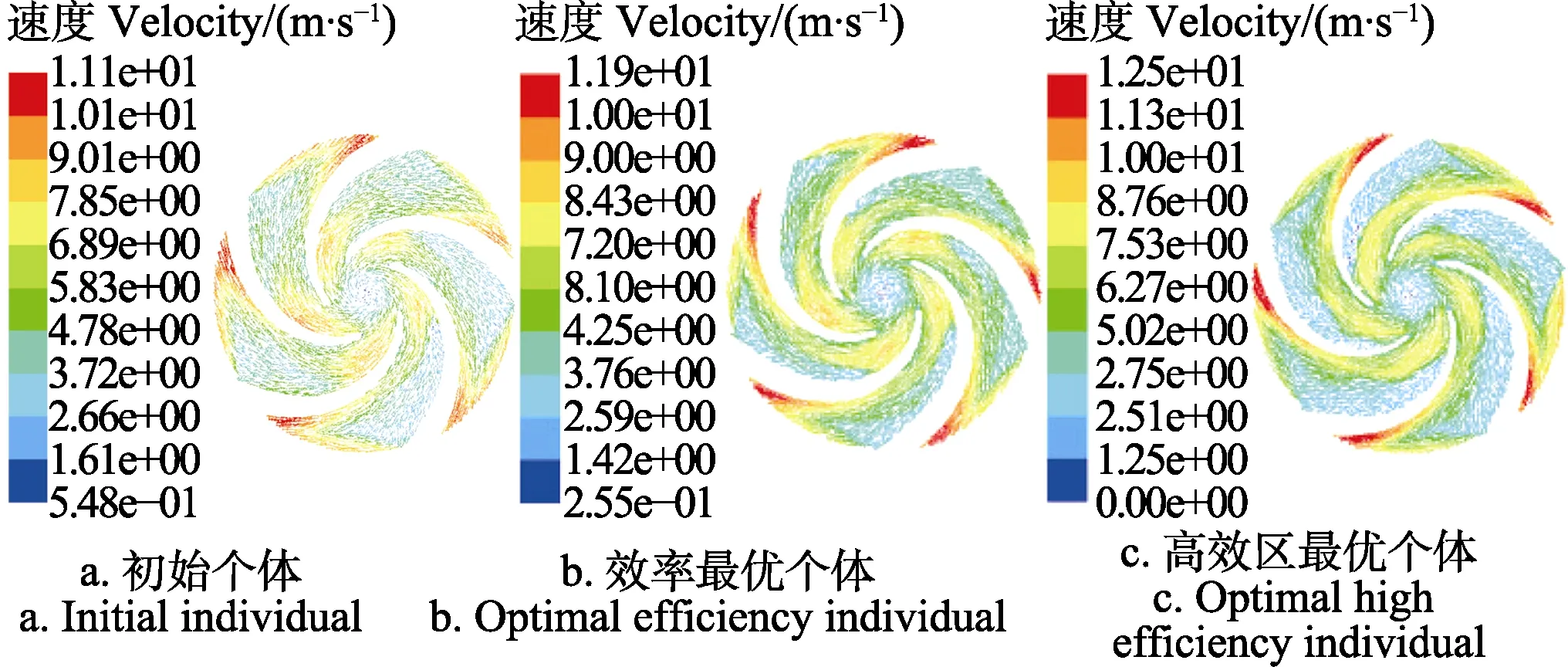
图8 NSGA-Ⅱ优化前后的叶轮中间剖面固相相对速度矢量对比图Fig.8 Comparison of relative velocity vector of solid phase at middle section of impeller between initial individual and optimal individual by NSGA-Ⅱ

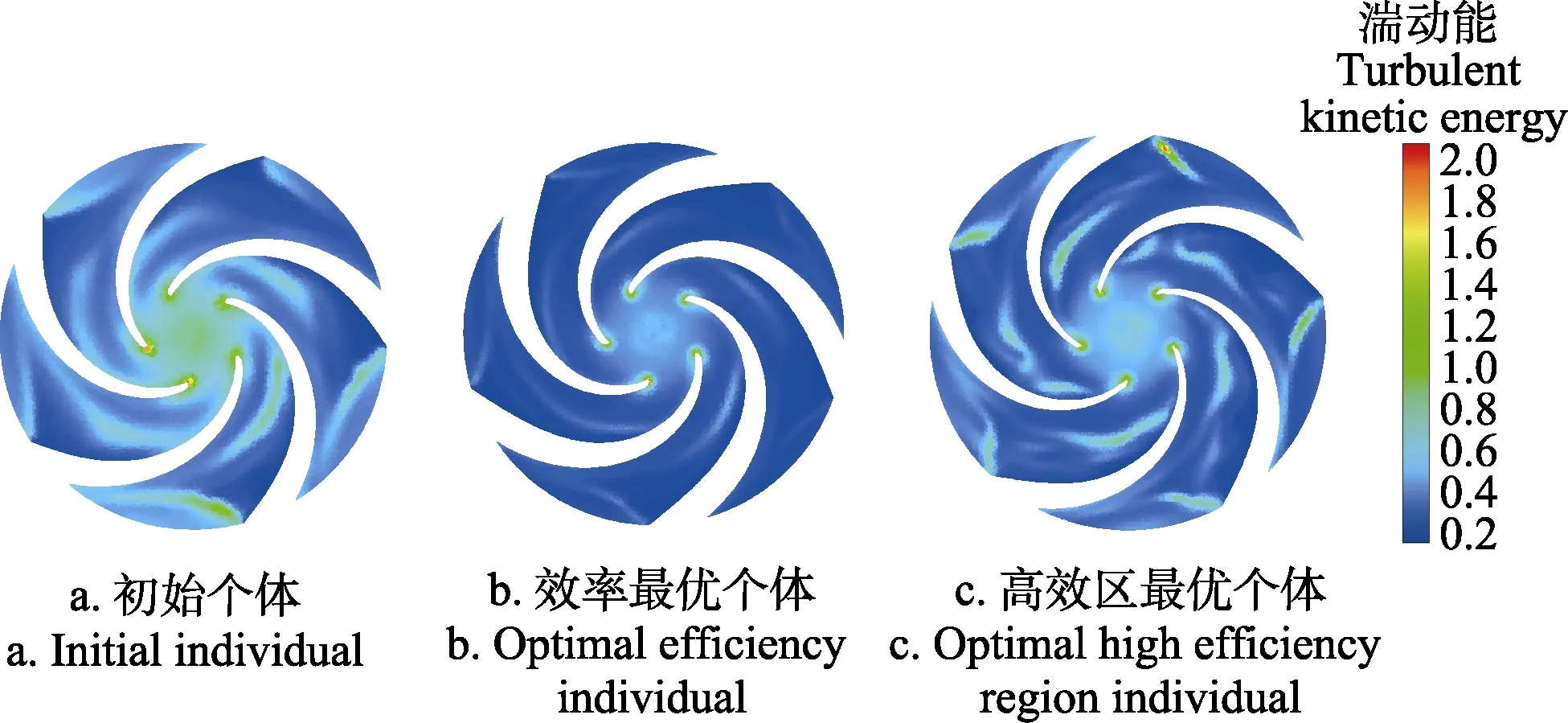
图9 NSGA-Ⅱ优化前后的叶轮中间剖面湍动能分布云图对比Fig.9 Comparison of turbulent kinetic energy distribution at middle section of impellers between initial individual and optimal individual by NSGA-Ⅱ

图8为优化前后3个个体的叶轮流道在中间剖面上的固相相对速度矢量图。3个个体的固相相对速度矢量趋势大体一致：叶轮进口靠近叶片背面相对速度有较大值，优化后的2个极值个体的相对速度在此处的值有所减小，叶片进口处的磨损性能得到了改善。从叶轮进口到出口，叶片工作面上相对速度逐渐增大，且变化的梯度比较明显，在叶轮出口与蜗壳进口的交界处达到最大值。固相流动叶片背面由于脱流形成的低速区范围较小，叶片背面靠近出口处没有漩涡产生。效率最优个体与高效区最优个体的固相相对速度矢量方向的趋势均比初始个体好，这表明流动状态更优。

图9为优化前后3个个体的叶轮流道在中间剖面上的湍动能分布云图。湍动能k是描述流场中湍流发展的一个重要指标，其值越小，表示流道内湍流发散的程度越小，叶片对流体做功的能力则越强。如图9所示，在叶片进口、靠近叶轮与蜗壳的交界面、叶片背面中段等位置湍动能值较大，这说明流体在上述位置的湍流程度较大，湍流脉动的脉动长度和时间尺度较大。优化前后的3个个体体湍流现象发生部位类似。高效区最优个的湍流发生区域范围较初始个体有明显的减小。效率最优个体的湍流发生区域范围则进一步缩小，有明显湍流部位仅为叶片的进口处。这说明优化后的2个叶轮对流体做功的能力均比初始个体强。

3.4 优化前后磨损特性对比

图10为优化前后3个个体叶片固相浓度分布图。由图可知，3个个体叶片上的固相浓度分布特征大体相似：叶片工作面上的固相浓度整体上高于叶片背面。叶片背面出口处浓度有最小值，叶轮进口处浓度有最大值，即叶轮进口处磨损严重。叶片靠近前盖板的一侧浓度低于靠近后盖板的一侧，这说明后盖板的磨损更为严重。

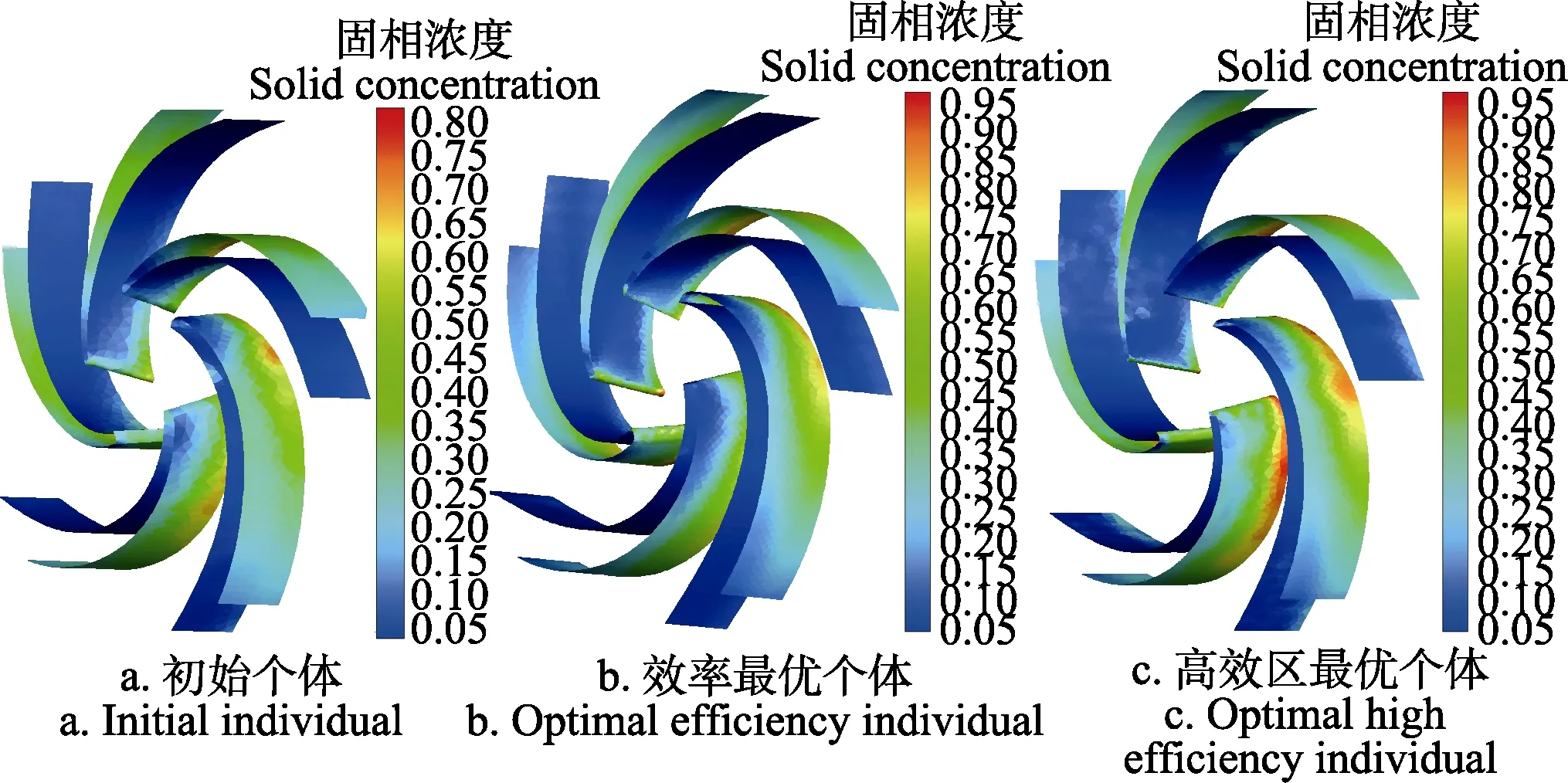
图10 NSGA-Ⅱ遗传算法优化前后的叶片固相浓度分布对比Fig.10 Comparison of solid concentration distribution on blades between initial individual and optimal individual by NSGA-Ⅱ

图11为优化前后3个个体叶片工作面的固相浓度分布图。叶片工作面上的固相浓度整体上较高，这是因为固相介质密度大于液相介质，叶片转动会对流体产生离心力，从而使得液相对固相约束力无法控制固相的流动。同时，沿半径方向叶片工作面与背面之间存在一定的压力差，因而沿叶轮流道扩散方向叶片工作面到叶片背面的固液分离趋于明显。沿前盖板至后盖板方向上，叶片工作面上的固相浓度逐渐增大，在靠近后盖板处叶片中段的位置存在一个固相聚集区域。其中，初始个体固相聚集的核心在叶片靠近后盖板位置约0.35倍包角处，最大浓度为0.65。效率最优个体为约0.2倍包角处，最大浓度为0.6，而高效区最优个体为约0.4倍包角处，最大浓度为0.9。这表明高效区最优个体的叶片工作面在运行时的磨损最为严重，效率最优个体的磨损较初始个体得到改善。

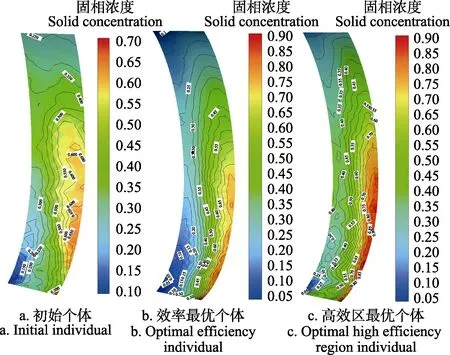
图11 NSGA-Ⅱ遗传算法优化前后的叶片工作面固相浓度分布对比Fig.11 Comparison of solid concentration distribution on pressure blades between initial individual and optimal individual by NSGA-Ⅱ

4 总结

1）本文运用 Design Expert 8.0.5b软件进行Placket t-Burman筛选试验设计，确定进口安放角β1、出口安放角β2、叶片包角φ为影响离心式渣浆泵最高效率与高效区的显著因素。

2）训练并测试RBF（radial basis function）神经网络，并以此作为评价适应度的响应模型，基于NSGA-Ⅱ遗传算法对离心式渣浆泵进行寻优计算。优化结果显示：效率最优个体的β2较初始个体有所减小，β1、φ则较初始个体有所增大，而高效区最优个体的进口安放角β1、出口安放角β2、叶片包角φ的大小较初始个体均有所减小。通过试验和模拟验证，证明结果有效。

3）取效率最优个体与高效区最优个体进行试验验证和数值模拟，并将其数据与初始个体的数据做对比：效率最优个体的最高效率较初始个体得到提升，但高效区略有减小；高效区最优个体最高效率较初始个体略有提高，但高效区范围增幅明显。通过对三者内部流场的分析与对比，可以得出：效率最优个体与高效区最优个体的固相相对速度矢量方向的趋势均比初始个体好；优化后的 2个叶轮对流体做功的能力均比初始个体强；高效区最优个体的叶片工作面在运行时的磨损较初始个体更加严重，而效率最优个体的磨损较初始个体得到改善。

[1]陶艺，袁寿其，张金凤，等. 渣浆泵叶叶轮磨损的数值模拟及试验[J]. 农业工程学报，2014，30(21)：63－69.Tao Yi, Yuan Shouqi, Zhang Jinfeng, et al. Numerical simulation and test on impeller wear of slurry pump[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(21): 63－69. (in Chinese with English abstract)

[2]彭维明，陈家远，程良骏，等. 水力机械固液两相流设计方法探讨[J]. 农业工程学报，1995，11(3)：129－132.Peng Weiming, Cheng Jiayuan, Cheng Liangjun, et al.Design method of two-phase flow in hydraulic machinery[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 1995, 11(3): 129－132. (in Chinese with English abstract)

[3]施卫东，邢津，张德胜，等. 后掠式叶片轴流泵固液两相流数值模拟与优化[J]. 农业工程学报，2014，30(11)：76－82.Shi Weidong, Xing Jin, Zhang Desheng, et al. Numeical simulation and optimization of solid-liquid two-phase turbulent flow in back swept axial pump[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(11): 76－82. (in Chinese with English abstract)

[4]刘栋，杨敏官，李辉，等. 化工泵叶轮内部固液两相流场的研究[J]. 水泵技术，2007，3：16－19.Liu Dong, Yang Minguan, Li Hui, et al. Study on solid-liquid two phase flow field in impeller of chemical pump[J]. Pump Technology, 2007, 3: 16－19. (in Chinese with English abstract)

[5]Ridgway N, Colby C B, O’Neill B K. Slurry pump gland seal wear [J]. Tribology International, 2009, 42(11): 1715－1721.

[6]Walker C I, Rpbbie P. Comparison of some laboratory wear tests and field wear in slurry pumps[J]. Wear, 2013, 302(1/2):1026－1034.

[7]汪家琼，叶群，闫科委，等. 颗粒直径对渣浆泵冲蚀磨损性能的影响[J]. 排灌机械工程学报，2014，32(10)：841－844.Wang Jiaqiong, Ye Qun, Yan Kewei, et al. Effects of particle diameter on erosion wear performance of slurry pump[J].Journal of Drainage and Irrigation Machinery Engineering,2014, 32(10): 841－844. (in Chinese with English abstract)

[8]李仁年，徐振法，韩伟，等. 渣浆泵内部流场数值模拟与磨损特性分析[J]. 排灌机械工程学报，2007，25(2)：5－8.Li Rennian, Xu Zhenfa, Han Wei, et al. Numerical simulation of interior flow and wear character in slurry pumps[J].Journal of Drainage and Irrigation Machinery Engineering,2007, 25(2): 5－8. (in Chinese with English abstract)

[9]何希杰，劳学苏. 离心泵系数法设计中的新统计曲线和公式[J]. 水泵技术，1997，5：30－37.He Xijie, Lao Xuesu. New statistical curves and formulas in the design of centrifugal pump coefficient method[J]. Pump Technology, 1997, 5: 30－37. (in Chinese with English abstract)

[10]张玉新，郭俊强. 固液两相流泵叶轮的优化设计方法[J].水泵技术，1997，6：21－26.Zhang Yuxin, Guo Junqing. Optimization design method of solid-liquid two phase flow pump impeller[J]. Pump Technology, 1997, 6: 21－26. (in Chinese with English abstract)

[11]朱艳姝，朱石沙，朱大洲，等. 基于遗传算法和 BP神经网络的离心泵性能预测[J]. 机械科学与技术，2012，31(8)：1274－1279.Zhu Yanshu, Zhu Shisha, Zhu Dazhou, et al. Predicting performance of centrifugal pump by combining genetic algorithm with BP neural network[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(8):1274－1279. (in Chinese with English abstract)

[12]Shahram D, Maryam P, Ehsan A，et al. Numerical shape optimization of a centrifugal pump impeller using artificial bee colony algorithm[J]. Computers & Fluids, 2013, 81(9):145－151.

[13]王春林，叶剑，曾成，等. 基于NSGA-Ⅱ遗传算法高比转速混流泵多目标优化设计[J]. 农业工程学报，2015，31(18)：100－106.Wang Chunlin, Ye Jian, Zeng Cheng, et al. Multi-objective optimum design of high spectific speed mixed flow pump based on NSGA-Ⅱgenetic algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(18): 100－106. (in Chinese with English abstract)

[14]王瑜. 基于多目标遗传算法的双流道泵叶轮水力优化设计研究[D].镇江：江苏大学，2015.Wang Yu. Study on Multi-objective Hydraulic Optimum Design of Double Channel Pump Impeller Based on Genetic Algorithm[D]. Zhenjiang: Jiangsu University, 2015. (in Chinese with English abstract)

[15]朱玉才，吴玉林，潘爱先，等. 离心式固液两相流泵叶片形状对流体动力特性影响的研究[J]. 机械工程学报，2004，40(8)：67－71.Zhu Yucai, Wu Yulin, Pan Aixian, et al. Influence of vane curve of solid liquid two-phase flow centrifugal pump of liqud-solid two-phase fluid on dynamic properties of fluid[J].Journal of Mechanical engineering, 2004, 40(8): 67－71. (in Chinese with English abstract)

[16]吴波. 离心式渣浆泵设计方法概述[J]. 矿山机械，2002(8)：45－47.Wu Bo. Summary of centrifugal slurry pump design method[J]. Mining & Processing Equipment, 2002(8): 45－47. (in Chinese with English abstract)

[17]郭晓民，贾宗谟. 渣浆泵设计方法的总结[J]. 流体机械，1996，24(1)：15－18.Guo Xiaomin, Jia Zongmo. Summary of slurry pump design method[J]. Fluid Machinery, 1996, 24(1): 15－18. (in Chinese with English abstract)

[18]吴波. 渣浆泵固液两相三维湍流及冲蚀磨损特性研究[D]长沙：中南大学，2010.Wu Bo. Study on Solid-liquid Two-phase Three-dimensionalTurbulence and Erosion Characteristics of Slurry Pump[D].Changsha: Central South University, 2010. (in Chinese with English abstract)

[19]吴玉林，曹树良，葛亮，等. 渣浆泵叶轮中固液两相湍流的计算和实验[J]. 清华大学学报，1998，38(1)：71－74.Wu Yulin, Cao Shuliang, Ge Liang, et al. Solid-liquid two-phase turbulent flow calculation and measurement through centrifugal slurry pump impellers[J]. Journal of Tsinghua University, 1998, 38(1): 71－74. (in Chinese with English abstract)

[20]Gonzalez J, Rojas I, Ortega J , et al. Multi-objective evolutionary optimization of the size, shape, and position parameters of radial basis function networks for function approximation[J]. IEEE Transactions on Neural Networks,2003, 14(6): 1478－1495.

[21]叶健，葛临东，吴月娴. 一种优化的RBF神经网络在调制识别中的应用[J]. 自动化学报，2007，33(6)：652－654.Ye Jian, Ge Lindong, Wu Yuexian. An application of improved RBF neural network in modulation recognition[J].Acta Automatica Sinica, 2007, 33(6): 652－654. (in Chinese with English abstract)

[22]Buzzi C, Grippo L, Sciandrone M. Convergent decomposi-tion techniques for training RBF neural networks[J]. Neural Computation, 2001, 13(8): 1891－1920.

[23]Esfe M H, Afrand M, Wongwises S, et al. Applications of feedforward multilayer perceptron artificial neural networks and empirical correlation for prediction of thermal conductivity of Mg(OH)2–EG using experimental data[J].International Communications in Heat and Mass Transfer,2015, 67(4): 46–50.

[24]Deb K, Parwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ [J]. IEEE Trans on Evolutionary Computation, 2002, 6(2): 182－197.

[25]Srinivas N, Deb K. Multiobjective function optimization using nondominated sorting genetic algorithms[J]. IEEE Transactions on Evolutionary Computation. 2000, 2(3): 1301–1308.

[26]玄光男，程润伟. 遗传算法与工程优化[M]. 北京：清华大学出版社，2004.

[27]李春明. 优化方法[M]. 南京：东南大学出版社，2009.

[28]刘媚. 混合 Pareto分布的统计分析[D].上海：华东师范大学，2009.Liu Mei. Statistical Analysis of Mixture Pareto Distribution[D]. Shanghai: East China Normal University,2009. (in Chinese with English abstract)

[29]Malik H J. Estimation of the parameters of the Pareto distribution[J]. Metrika, 1970, 15: 126－132.

[30]Yazici B, Kan B. Asymmetric control limits for small samples[J]. Qual Quant. 2009, 43: 865－874.

Multi-objective parameters optimization of centrifugal slurry pump based on RBF neural network and NSGA-Ⅱ genetic algorithm

Wang Chunlin, Feng Yiming, Ye Jian, Luo Bo, Liu Keke
(School of Energy and Power engineering, Jiangsu University, Zhenjiang212013,China)

With the rapid development of national industry and mining, slurry pump is widely applied in transportation of two-phase flow as a sort of practical and reliable fluid machinery. Due to that the medium of centrifugal slurry pumps transport is fluid-solid two-phase medium, there is great difference for internal flow field between centrifugal slurry pumps and clean water pumps. Therefore, the design of the former is more complex and its design theory and method are not perfect now. In terms of performance, the main criticisms are its working head lower than design head, low efficiency and severe wear. So, it is a kind of equipment whose performance should be promoted rapidly in modern safe and effective industrial production.Thus, the optimal design of centrifugal slurry pumps is very meaningful for improving its performance. A centrifugal slurry pump with a specific speed of 75 was chosen as the research object. With the commercial CFD (computational fluid dynamics)software Fluent, RNGk-εturbulence model and Eulerian two-phase flow model were selected to calculate its internal flow.The efficiency and the high efficiency region of the centrifugal slurry pump were set as the optimization goal. Design Expert 8.0.5b was used to make Plackett-Burman screening experimental design to pick out 3 structural parameters from 12 structural parameters of model pump, which were slurry pump blade inlet angle, outlet angle and wrap angle, set as the optimization variables, because too many structural parameters may affect the high efficiency area and the highest efficiency of centrifugal slurry pump. The 37-level uniform experiment was finished and the training and testing samples of RBF neural network were established. RBF (radial basis function) neural network was used to fit the relationship between the variables and objectives,which could be applied in NSGA-Ⅱ algorithm to get the Pareto optimal solution. Aiming at the result of the optional Pareto solution set, the optimal efficiency individual and high efficiency region individual were selected to compare with the initial model that was not optimized: The difference of external characteristic curves, distribution of absolute pressure at middle section of impeller runner and volute runner, relative velocity vector of fluid and solid phase, distribution of turbulence kinetic energy, distribution of solid concentration of pressure blades, blades back, front shroud and back shroud at middle section of impeller runner were all compared between the 2 extreme value individuals and initial individual. According to the analysis results of the differences between the performance curves of the above 3 individuals, the obtained optimal efficiency blade inlet angle, outlet angle and wrap angle were 21.76°, 23.43°, and 145.56°, respectively, and the high efficiency region blade inlet angle, outlet angle and wrap angle were 19.38°, 22.68°, and 116.71°, respectively. The experiment proved that the efficiency of the optimal individual was improved by 3.81% and the high efficiency region individual was improved by 4.33%compared with the original individual. The optimization results show that this optimization method improves the hydraulic characteristics of the impeller and the performance of centrifugal slurry pump.

pumps; numerical simulation; optimization; RBF neural network; NSGA-Ⅱ genetic algorithm; multi-objective optimum

10.11975/j.issn.1002-6819.2017.10.014

TH313

A

1002-6819(2017)-10-0109-07

2016-09-12

2017-04-13

国家自然科学基金资助项目（51109094）；江苏高校优势学科建设工程项目

王春林，男，江苏盐城人，教授，主要从事流体机械理论、特性及流动模拟的研究。镇江 江苏大学能源工程与动力学院，212013。

Email：chwang@ujs.edu.cn