土体冻结过程中基质势与水分迁移及冻胀的关系

薛 珂，温 智，张明礼，李德生，高 樯

（1. 中国科学院西北生态环境资源研究院冻土工程国家重点实验室，兰州 730000；2. 中国科学院大学，北京 100049；3. 兰州理工大学土木工程学院，兰州 730050）

土体冻结过程中基质势与水分迁移及冻胀的关系

薛 珂1,2，温 智1※，张明礼3，李德生1,2，高 樯1,2

（1. 中国科学院西北生态环境资源研究院冻土工程国家重点实验室，兰州 730000；2. 中国科学院大学，北京 100049；3. 兰州理工大学土木工程学院，兰州 730050）

土体冻结过程中不同位置液态水的能量差引起了水分迁移与重分布，进而引发冻胀，关于势能差驱动下的冻土水分迁移问题一直由于技术手段的匮乏而没有完全解决。利用新近推出的可用于冻土水热研究的pF meter基质势传感器与5TM水分传感器，实时监测研究饱和青藏红黏土单向冻结过程中基质势-液态含水率-温度-含冰量-水分迁移量-冻胀变形之间在时间、空间上的耦合变化关系。结果表明：土体温度场变化引起内部液态水相变，打破了原有的能量平衡，试验结束后12～14 cm土样高处含水率最高达到55%，靠近冻融交界面处（10 cm）的未冻区含水率减小至25.8 %，水分整体向冷端发生迁移；土体冻胀的快慢及冻胀量大小与水分迁移速率及数量具有线性关系；试验后土体内总含水率的分布与分凝冰透镜体的分布一致，已冻区液态含水率的分布与温度梯度近似成线性关系，未冻区液态含水率的分布与水分的迁移量有关，与温度梯度无关。此外，温度场对水分场的变化具有诱导作用但二者并不同步，当冻结速率减小到一定程度时水分才开始迁移，第10小时后温度场趋于稳定而水分迁移并未停止。研究成果揭示了土体单向冻结过程中液态水、基质势、温度等物理参数的动态变化过程及内在联系，为冻胀机制的研究以及冻胀模型的建立提供了试验基础。

土壤；冻结；含水率；温度；冻胀；分凝冰；基质势；pF meter

薛 珂，温 智，张明礼，李德生，高 樯. 土体冻结过程中基质势与水分迁移及冻胀的关系[J]. 农业工程学报，2017，33(10)：176－183. doi：10.11975/j.issn.1002-6819.2017.10.023 http://www.tcsae.org

Xue Ke, Wen Zhi, Zhang Mingli, Li Desheng, Gao Qiang. Relationship between matric potential, moisture migration and frost heave in freezing process of soil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE),2017, 33(10): 176－183. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.10.023 http://www.tcsae.org

0 引 言

土体的冻胀破坏是寒区最常见的工程病害之一。冻胀作用除了对地表构筑物及埋置于地下的诸如地热管等设施造成破坏之外，还会改变土壤含水率及水分的分布状况，对农业种植等都有一定的影响。关于土体冻胀的研究，最早开始于19世纪20年代[1-3]，冻胀是一个复杂的相变、热传递、力和水分运动的过程[4-6]。冻胀的形成与土冻结时孔隙水的原位冻结有关，发生于冻结过程中的水分迁移是导致冻胀的最主要因素[7-11]。若要掌握冻胀的发生过程与机理，必须首先深入理解水分迁移的过程及其具体的驱动原因与相关机制[12-15]。

从19世纪末至今，众多学者提出了各种关于冻土水分迁移驱动力的假说，如毛细管作用力理论[16-17]、薄膜水迁移理论[18]、结晶力理论、吸附-薄膜迁移理论[19-20]，此外，还有吮吸力理论、气压液泡理论、冰压力梯度理论等各类假说。事实上，土体发生冻结时，液态水在迁移过程中受到很多力的作用和影响，包括重力、吸附力、毛管力、渗透力等[21]。不同形式的力，对液态水的运移有着不同的作用。正冻土中水分的迁移是多因素共同作用的结果，是各种单因素对水分迁移的综合效应[22]。

整合之前的相关假设，从能量的角度出发研究正冻土中水分迁移的机制，为解释相关研究现象提供了一个全新的视角，而且很好地弥补了之前各种学说的不足，进而解释土中水分迁移的驱动过程。基质势作为描述土中水能量状态的重要参数，主要由吸附势与毛管势组成[23]。早在1907年，Buckingham[24]认为单位时间通过单位面积的水流与某一函数的梯度成正比，并把这个函数称为毛细管势。此外，Schofield[25]提出了pF的概念，将单位cm高水柱中的吸力定义为pF，Croney等[26]在此基础上提出了冰点降低法利用Clapyron方程将冻结过程的温度变化关系转变为水势变化，通过这种间接的方法来获得冻土中液态含水率与势能之间的变化关系。

在一般融土中，基质势常用张力计法、滤纸法等直接测定，在极端负温条件下的含冰土体中很难被应用。因而，长期以来因缺乏可靠测量手段，冻土中的基质势难以被直接测定，更多地是利用间接法换算推导得到，而间接法得到的冻土基质势并非真实的试验值，其可靠性有待考证。

近几年pF meter基质势传感器被越来越多的学者应用到冻土研究中。温智等[27]证实了pF meter基质势传感器在冻土水热研究的可行性。然而，针对土体冻结过程中基质势-液态水-温度-冻胀变形之间相互耦合关系以及冻结锋面附近水分的运移状况研究并不全面，包括基质势驱动作用下的正冻土水分迁移过程以及冻胀机制一直缺乏有力的验证。

基于此，本研究利用经过微型化改造后的pF meter基质势传感器（微型化以更适应室内试验）以及 5TM 水分传感器，通过饱和青藏红黏土单向冻结试验，分析冻土水热迁移耦合过程，研究基质势-液态水-温度-含冰量-水分迁移量-冻胀变形之间在时间、空间上的耦合变化关系，进而深入了解土体冻结时基质势在水分运移过程中的作用，以期揭示土体冻结过程中液态水、基质势、温度等物理参数的动态变化过程及内在联系，为冻胀机制的研究以及冻胀模型的建立提供了试验基础。

1 材料与方法

1.1 供试材料

考虑到土体冻胀的敏感性，试验采用取自青藏高原北麓河地区青藏铁路沿线附近场地的具典型冻胀特性的红黏土。青藏红黏土呈褐红色，具强黏性，其粒径级配组成中＜0.005 mm的土颗粒占44.69%， 0.05～＜0.1 mm间的土颗粒占52.65%，≥0.1 mm的土颗粒占2.66%，其干密度为1.33 g/cm3，饱和质量含水率为33%，液限、塑限分别为37%、22%。此外，经测定得到青藏红黏土的初始冻结温度为–0.51 ℃。

1.2 试验方法

1.2.1 试验设备

1）微型pF meter基质势传感器

试验采用经微型化改造后的pF meter基质势传感器实时监测基质势的动态变化情况（图1）。该传感器为德国Eco-Tech生产并按照我方要求，从原始规格80 mm´20 mm微型化改造为20 mm´18 mm，以更适应土体冻胀的室内试验研究（专利号：DE10164018B4）。该传感器基于摩尔热容原理，借助于特殊设计的陶瓷平衡系统，通过测量加热前后的热容变化得到基质势。测量温度范围为–40～80 ℃，精度为±0.05 ℃。pF meter操作简便，在使用中免除了传统张力计使用时需要注水维护的不便，直接使用数字信号输出 pF值，适用于干旱地区、冻土、路基等其他特殊领域土壤水的研究。其中，关于微型化后的pF meter在冻土基质势研究中的可行性，温智等[27-28]已开展了相关工作并认为pF meter适用于冻土水热的研究。

2）5TM土壤水分传感器

试验使用Decagon公司生产的5TM土壤水分传感器来获得土体冻结过程中不同位置的液态含水率[29-30]，其测量范围为 0～100%，工作的温度范围为–40～50 ℃，该传感器可被应用于冻土水热研究中[31]。

3）其他试验装置

为方便pF meter基质势探头的安置以及完整获取冻后土体冷生构造发育情况，专门设计制作了可张合有机玻璃容器（图1），其尺寸为：高30 cm，内径16 cm，外径18 cm。另外，本试验全过程在XT5405系列的Xutemp冻融循环箱内完成，试验时将罐体加上下顶板后置于冻融循环箱内进行试验（图1）。

图1 单向冻结试验装置及微型化后的基质势传感器Fig.1 Apparatus of one-dimension freezing test and miniaturized matric potential sensor

1.2.2 试验方案

饱和试样可以排除土中的气相的干扰，简化试验结果分析的复杂性，因而试验采用饱和土体作为研究对象。采用8枚pF meter基质势传感器以及8枚5TM土壤水分传感器，将它们分层等距安置在改造后的透明有机玻璃试样罐内，垂向间距均2 cm，第1枚探头与最后1枚探头离上下顶板均为2 cm（图2）。试样罐上下均为可施加热传导的冷浴系统，通过冷浴控温，设置顶/底板温度分别为–5 ℃/2 ℃，采用从上至下单向冻结的方式，初始温度为22 ℃。为保证冻结稳定后在土体纵剖面上形成较合理的温度梯度（冻结深度不会过大/过小，以及形成高度适合的冻结区/未冻区），基于与预试验结果，设置顶/底板温度分别为–5 ℃/2 ℃。

整个试验在冻融循环箱内进行，考虑到试验过程中土体可能受到的径向热传导，为尽量减小其影响，首先设置箱体温度为2 ℃（与土样底板温度相同），其次，在土样内安置传感器时尽量将所有传感器的位置固定在不同高度的同一位置处，保证传感器沿垂直方向的位置一致，这样可以降低因为径向热传导带来的径向不同半径处的冻结状况不一致的现象。此外，在试样和设备安装完毕之后，使用双层隔热保温海绵将试样罐进行包裹，尽量保证土体的一维垂向冻结。另外，采用开放系统下边界补水方式，使用马廖特瓶从土样底端为土体进行补水。

试验中，使用pF meter获取基质势，使用5TM土壤水分传感器获得液态含水率以及温度变化情况，使用位移计获取冻胀量并人工记录马廖特瓶内的水位数据得到累计补水入流量；试验后，打开可张合有机玻璃试样罐取出完整的冻后土样，并使用尼康数码相机（型号：Coolpix A100）拍照得到冷生构造分布情况；另外，用烘干法测定试样剖面上总含水率（液态含水率与含冰量之和）。

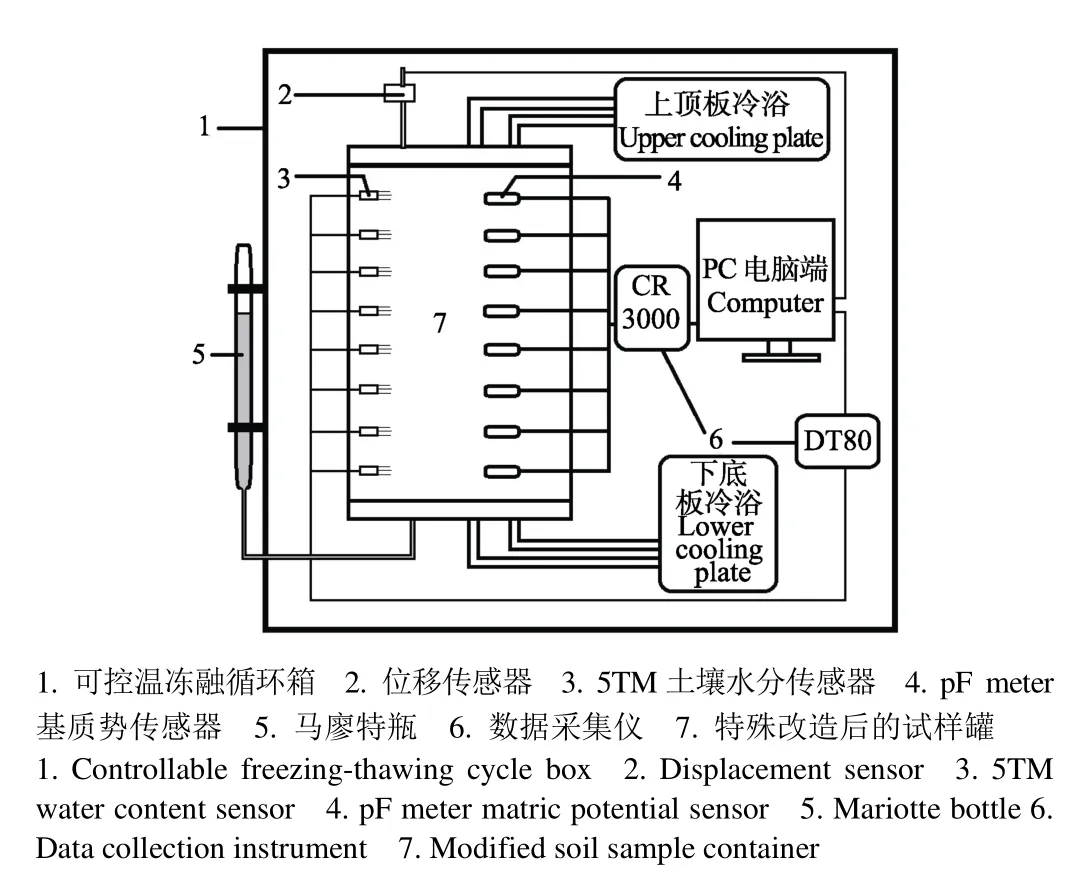
图2 单向冻结试验示意图Fig.2 Schematic of one-dimensional freezing experiment

1.2.3 试验步骤

1）制备样品。将青藏红黏土晒干、碾碎、过筛（2 mm）后制备成饱和试样并置于密封罐中闷样12 h以上，使得水分与土颗粒完全均匀接触；2）装样。将闷样完成后的土样进行分层装样，以确保样品均匀各向同性。样高18 cm、直径16 cm。在土样两端加透水石并将其固定，将有机玻璃容器整个放入真空缸内进行真空抽气 5 h使得土体内空气完全被排除，完成上述工作后，将试样连接好顶/底板冷浴并连接pF meter与5TM的数采仪、补水管以及冻胀位移传感器。关闭冻融循环箱开始试验。

2 结果与分析

2.1 土体单向冻结过程与温度分布

2.1.1 冻结过程中土体内温度场的变化

图3为土样冻结过程中土体温度分布。

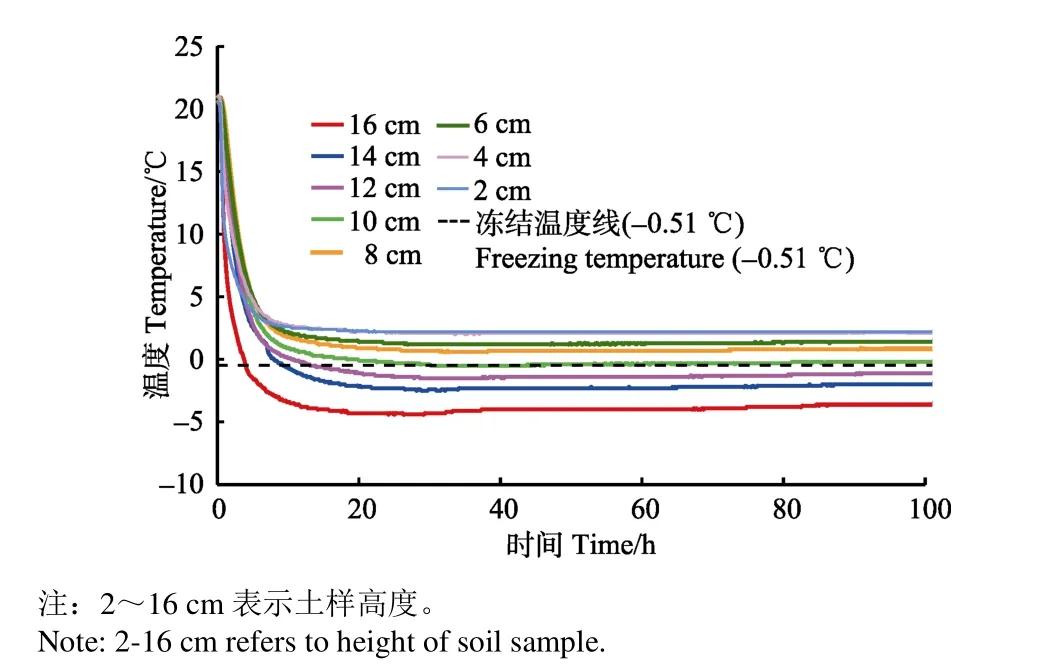
图3 土样冻结过程中的温度分布Fig.3 Temperature distribution during freezing of soil sample

试验采用单向冻结方式，土体从上至下依次冻结。试验开始以后，土体温度从室温（22 ℃）开始降低（图3）。从冻结开始后的第4小时，土柱16 cm处开始率先冻结。此时，温度梯度较大，土体顶端温度迅速由正温变为负温，这部分土体内液态水发生相变，由于冻结速率较快，液态水直接在土孔隙中发生原位冻结。此外，土体中温度达到–0.51 ℃之后开始冻结，冻结顺序从上至下，冻结至10 cm土柱高处，冻结深度不再发生变化，土柱中温度场逐渐趋于稳定。

2.1.2 冻结锋面的迁移过程

根据青藏红黏土的冻结温度–0.51 ℃，绘制–0.51 ℃等温线，获得土体冻结过程中冻结锋面（冻土与非冻土之间可移动的接触界面）的变化曲线（图 4）。试验开始时，冻结锋面迅速向下推进，冻结速率大，随着时间的推移以及冻结深度的增加，冻结速率减慢，自35 h以后，冻结锋面的位置趋于稳定，冻结速率趋于0，冻结深度不再变化。从图 4可以看出，冻结锋面稳定之后，冻融交界面停在了10 cm高处附近。

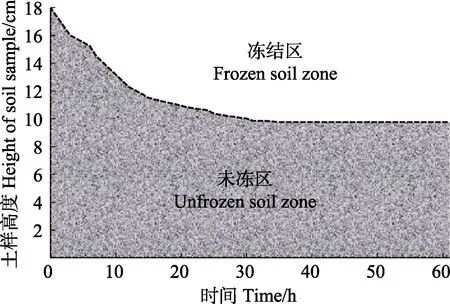
图4 冻结锋面动态变化Fig.4 Dynamic change in freezing front position

2.2 冻结过程中土体内水分场的变化

土体冻结时内部液态含水率的变化与温度场的变化相关联。图 5为不同时刻土体内液态含水率随温度与时间的变化曲线。试验开始时，土体内液态含水率基本保持一致，在试验进行到3 h时，靠近顶部的16 cm处率先开始大幅减小，8 h时，16 cm处液态含水率已经基本达到稳定后的状态；同时，靠近底部的2 cm高处液态含水率缓慢减小，减小幅度较小；土体内水分场稳定后液态含水率分布基本呈线性，除了8 cm高处液态含水率略大于6 cm高处之外，其他各位置液态含水率的分布与土体高度成反比。

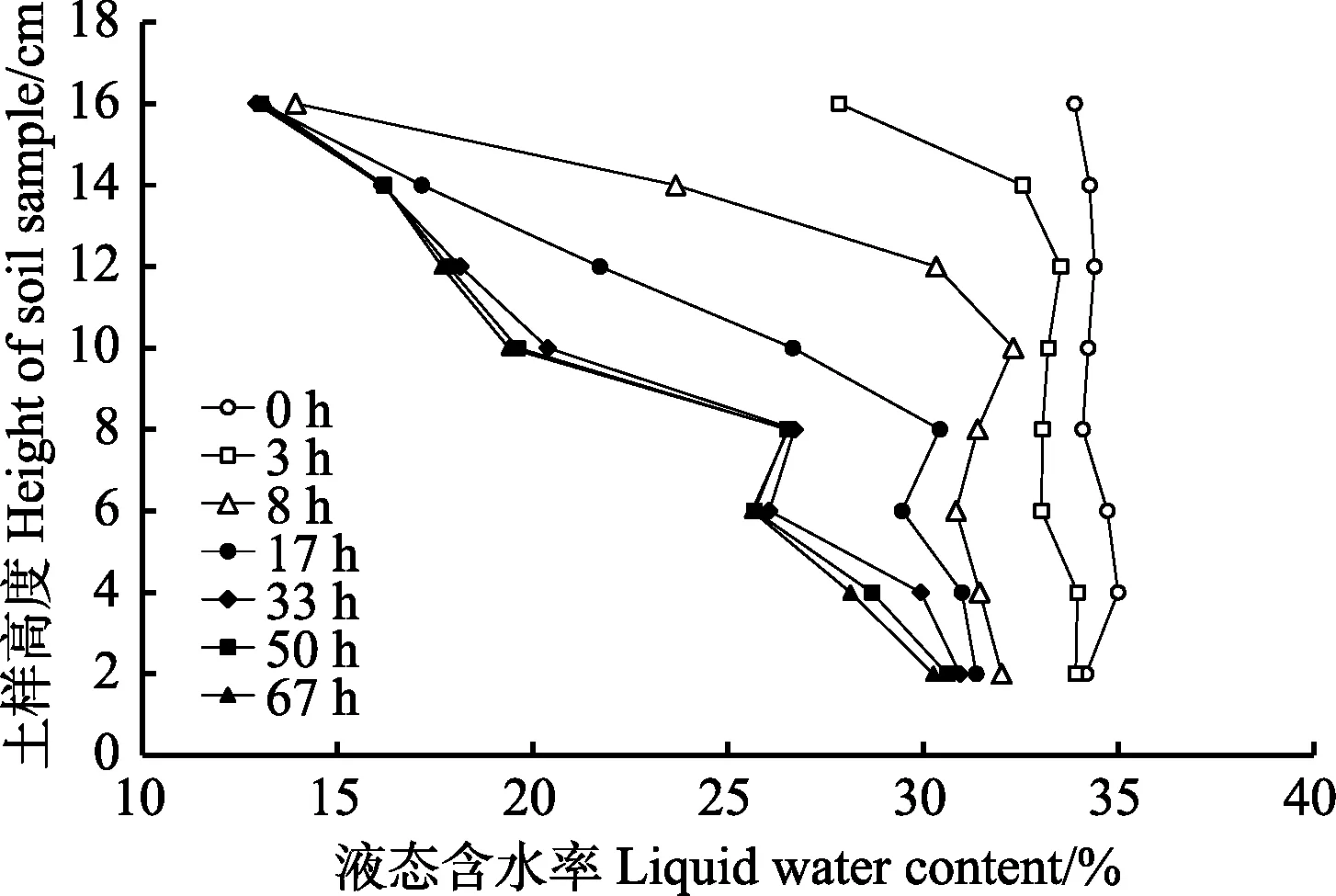
图5 不同时刻土柱中液态含水率Fig.5 Liquid water content of soil sample in different times

试验结束后使用烘干法测得纵剖面上含水率（液态含水率与含冰量之和），结合 5TM 土壤水分传感器测得的试验后液态含水率以及试验开始时纵剖面上的初始含水率（图 6），比较后发现试验结束后土柱上部总含水率明显增大，在10～14 cm高处，含水率最高达到55%左右；而在土柱下部，含水率要小于初始含水率，尤其是在6 cm高处测得的含水率为25.8%，其值明显小于其余各位置的值。说明在冻结过程中，水分的确向冻结区发生了迁移，同时，液态含水率的分布只与温度梯度有关，与水分迁移无关。

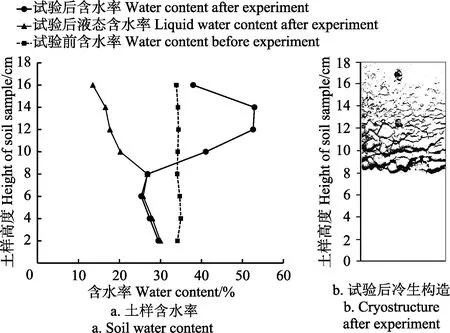
图6 试验前后土样含水率及试验后冷生构造分布Fig.6 Soil water content before and after experiment and cryostructure after experiment

2.3 冻胀量和累计补水入流量

土体的冻胀量和补水情况如图7所示。

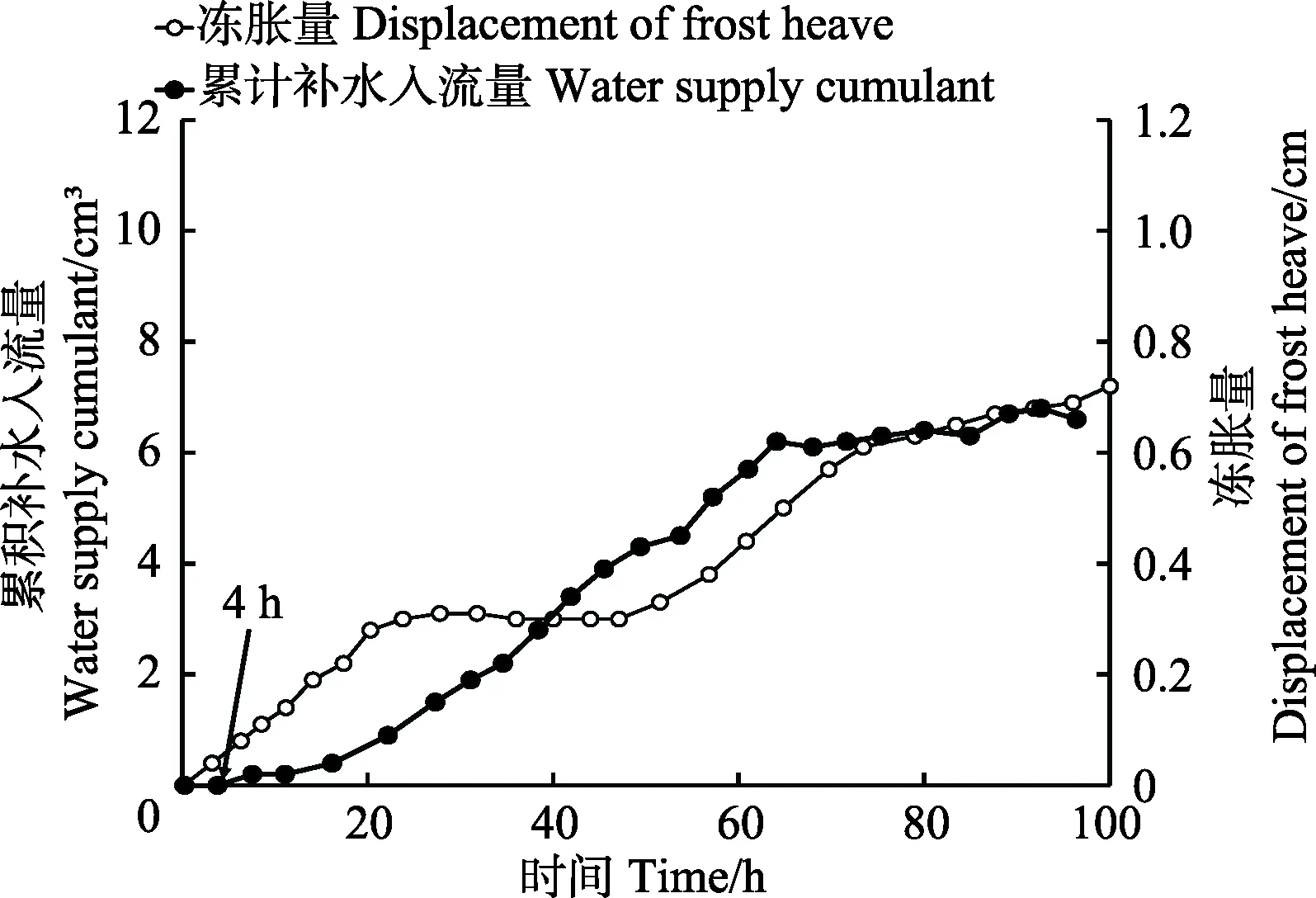
图7 冻胀量与累积补水入流量随时间的变化Fig.7 Variation of frozen heave displacement and water supply cumulant with time

从图7可以看出，冻胀过程大致可以分为3个阶段：在冻结初期（0～4 h），累计补水入流量为 0，这是由于当温度梯度过大，冻结速率较大且冻结锋面迅速移动时，土体来不及从下部吸水，此时不发生冻胀；在冻结后期（4～60 h），土体内的水热变化最为剧烈，水分的运移和重分布活动也非常剧烈，冻胀量快速增大，此时，靠近冻结锋面处形成的冰透镜体不断地从冻结缘区进行吸水，冰透镜体厚度持续增加，从宏观上造成冻胀现象；冻胀量的增加速率在60 h以后开始减小，此时土体内的水热交换逐渐达到稳定状态，水分运移开始减慢，冻胀量也基本上不再有较大的增加。

2.4 基质势变化

图 8为土体冻结过程中基质势的变化。可以看出，试验开始阶段，土柱中各位置的土体均处于饱和状态，此时各处的基质势值均为0。随着温度自上而下降低，从土体上部开始往下各位置的基质势依次开始从 0减小，基质势值从 0开始变化的时刻就是该处土体中液态水发生冻结的时刻。

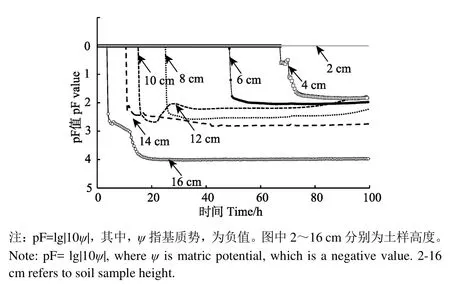
图8 土体冻结过程中基质势的变化Fig.8 Variation of matric potential during freezing

同样，受冻结速率和温度梯度的影响，首先，越靠近顶端的土体中相邻两处基质势从 0开始降低的时间间隔越短，反之，离顶端越远，相邻两处基质势从0开始变化的时间间隔越大；其次，土体内温度场稳定之后（10 h），基质势的值与该处液态含水率相对应，液态含水率越小，基质势也越小。

2.5 单向冻结后土体中的冷生构造

图 9为试验后土体沿纵剖面的冷生构造发育情况,其中黑色部分为分凝冰透镜体。可以看到，冻结后土体可分为原位冻结带，纤维状构造带，层状构造带及未冻土带。在靠近顶端的一定深度内，肉眼基本看不到冰晶的存在，这是由于冻结开始时，温度梯度大，冻结迅速，水分来不及发生迁移，只在原位发生冻结所致，这部分为原位冻结带；在原位冻结带下方，出现纤维状构造带，纤维构造带内存在密集分布的超薄冰片，这是由于整体构造带形成之后，土体热阻增大，冻结速率有所减慢，冻结锋面向下发展的速度也相应减小，但总体来说，冻结速率还是较快，水分的迁移并不显著；在冻融分界面和纤维构造带之间形成了分布有层状冰透镜体的层状构造带，在该带内自上而下层状分凝冰厚度逐渐增大，分凝冰层之间的间距也逐层增大，这些分凝冰透镜体的来源为下部未冻区液态水的迁移补给，当冻结锋面抵达这一区域时，温度梯度已经相对变小，冻结速率缓慢，冻结锋面向下发展的速率也逐渐减小，这为液态水从未冻区向冻结锋面的迁移提供了充足的时间。

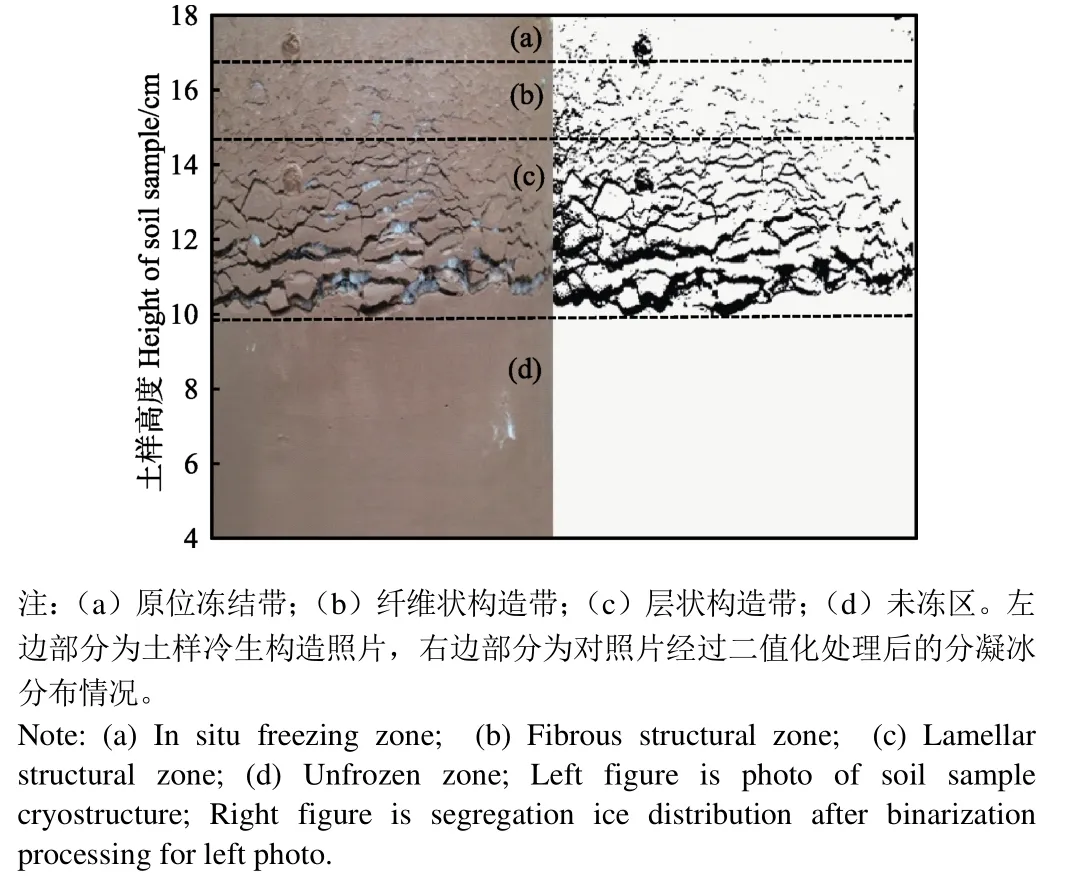
图9 单向冻结试验后土体的冷生构造Fig.9 Soil sample cryostructure after one-dimensional freezing experiment

2.6 温度场、水分场及基质势在冻结过程中的变化关系

土体冻结过程中，其温度场-水分场-基质势之间具有相互耦合的关系，从三者之间的因果关系来讲，首先是土体温度场的改变，导致了土中液态水相变，液态水发生相变后又导致了土体不同位置的液态水所具有的能量状态发生了改变，之前土中水的稳定状态遭到了破坏，为了保持能量平衡，土中液态水开始从高势能位置向低势能位置发生迁移。图10为土体10 cm及其以上部分在冻结过程中温度，水分，基质势的变化情况。从图中可以看出，三者随时间变化的趋势上具有相似的形态，随着温度降低，液态含水率减小，基质势也从 0开始变为负值，而且各物理量在具体的数值上与土体的温度梯度及冻结速率呈比例关系。可以看出，基质势与温度的变化一致，当土体温度达到冻结温度时，土孔隙中出现冰晶，此时土体基质势从 0开始减小为负值，土体中个位置基质势从 0开始减小的时间与该位置土体开始冻结的时间一致。同样，基质势对冻结过程中液态水数量变化及其运移也具有响应作用。冻结前期，已冻区液态含水率减小，冻结锋面下方土体基质势持续为0，20 h时，靠近顶板处土体基质势达到－1 000 kPa左右，土样14、12、10 cm高处分别减小至－55、－47.5、－30.2 kPa。当冻结速率开始减慢，分凝冰开始生长时，液态水向上发生迁移，同时，冻结锋面下方的基质势持续减小，这是由于未冻区液态水向已冻区发生迁移造成，说明水分迁移需要同时满足相邻位置之间的基质势差以及充足的时间这2个条件。

需要注意的是，土体中液态含水率的变化与温度虽然在形态上具有相似性，但液态含水率开始减小的时刻却要提前于土体开始冻结的时刻，这是因为上部土体冻结后，有少量液态水向上迁移，从图10中可以看出，各位置液态含水率在微量的减小之后，减小的速率开始降低，而当该位置土体温度达到冻结温度之后，液态含水率又明显加速减小，分析原因，这是由于前半部分的液态含水率减小与水分的向上迁移有关，而后半部分的液态含水率减小与该位置土体的冻结程度有关。

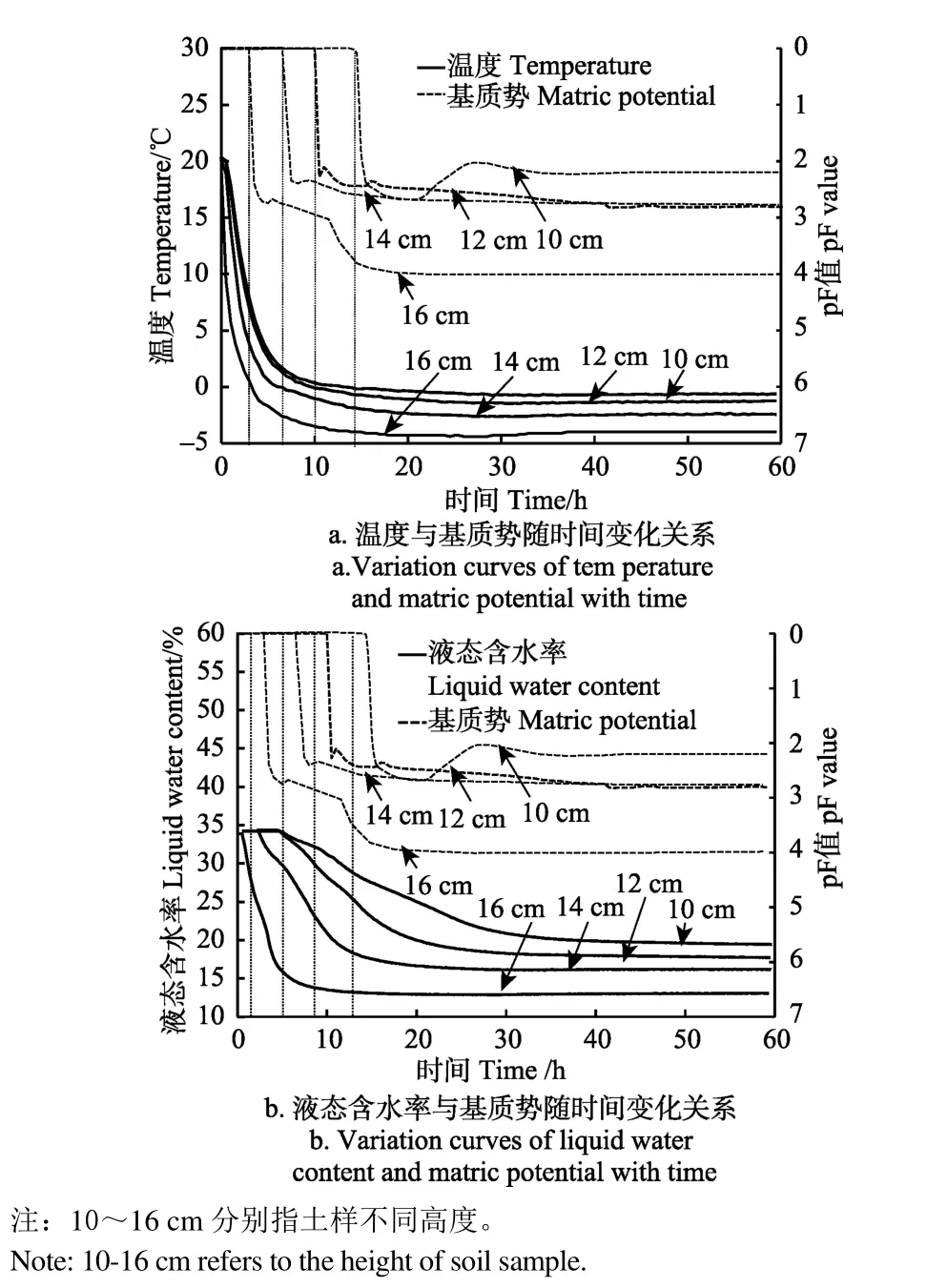
图10 冻结区土体冻结过程中温度、液态含水率、基质势的变化Fig.10 Variation of temperature, liquid water content and matric potential in frozen region during soil freezing

2.7 水分场的变化与土体的冷生构造之间的关系

土体的冻结是一个热质输运的耦合过程。冻结区分凝冰透镜体的主要成因为土体中液态水的迁移，当土体温度达到冻结温度后，孔隙中的液态水相变为冰晶，将土颗粒胶结为一体，此时土颗粒表面仍有部分未冻液态水膜紧密的包裹在土颗粒周围，同时，该位置的液态水膜的自由能大大降低，基于能量平衡，液态水从未冻区向已冻区进行迁移，以弥补冻结区由于液态水相变为冰晶造成的水分损失，从而，在已冻区某位置形成垂直于热流和水流方向的分凝冰透镜体。

从图 6可以看出，试验前（未发生冻结时）土体各位置液态含水率基本一致，冻结后土体内液态含水率基本与温度梯度成比例关系。土体内液态含水率在土体冻结后整体减小，对于冻结区而言，各位置减小的液态水一部分向上发生了迁移，另一部分在原位发生冻结，对于未冻结区而言，土中的液态水减小量全部用于水分向冻结区的迁移。比较水分迁移量和分凝冰的分布关系发现，靠近冻融分界面（10 cm）以上2 cm厚的区域内含水率最大，水分迁移量与土体的冻结速率关系紧密，冻结速率的大小决定了液态水是否具有充足的时间向已冻区进行迁移，当冻结锋面发展到10 cm左右时，冻结锋面基本上停止进一步的发展，冻结速率也缓慢减小至0，此时冻融交界面处的液态水能量并不平衡，通过水分向冻结锋面后方进行迁移，经过一定时间以后，冻融交界面处的液态水处于一种亚平衡状态，此后，水分停止迁移，整个土体内的水分趋于稳定，这也解释了温度场稳定后水分继续发生向上迁移的原因。

2.8 水分迁移与基质势之间的关系

与融土类似，冻土中水分迁移也是由于相邻土体内液态水之间存在的势能差引起。图11为土体冻结过程中冻结缘附近区域的示意图。冻结锋面与最暖端冰透镜体之间的区域被称之为冻结缘，冻结缘被认为是冻土水热迁移最为剧烈的区域。与融土不同的是，冰的存在使得冻土的物理性质变得极为特殊，由外界温度诱导而萌发的冰晶体一方面改变了该位置液态水的能量状态，另一方面可能会增加水分迁移的阻力改变土体的渗透性。事实上，土体孔隙中完全被冰填充之后，由于缺乏顺畅的迁移通道，液态水很难进行水分的运移，真正存在大量水分迁移的区域正好是冻结缘区。如图11所示，冰透镜体暖端和初始温度等温面之间存在较大的基质势梯度，同时初始冻结温度等温面上土体大孔隙内冰晶体刚刚萌发，而分凝冰透镜体暖端基质势较小，在这种势能梯度下，液态水源源不断地从冻结锋面下方的冻区迁移至分凝冰处形成冰透镜体。

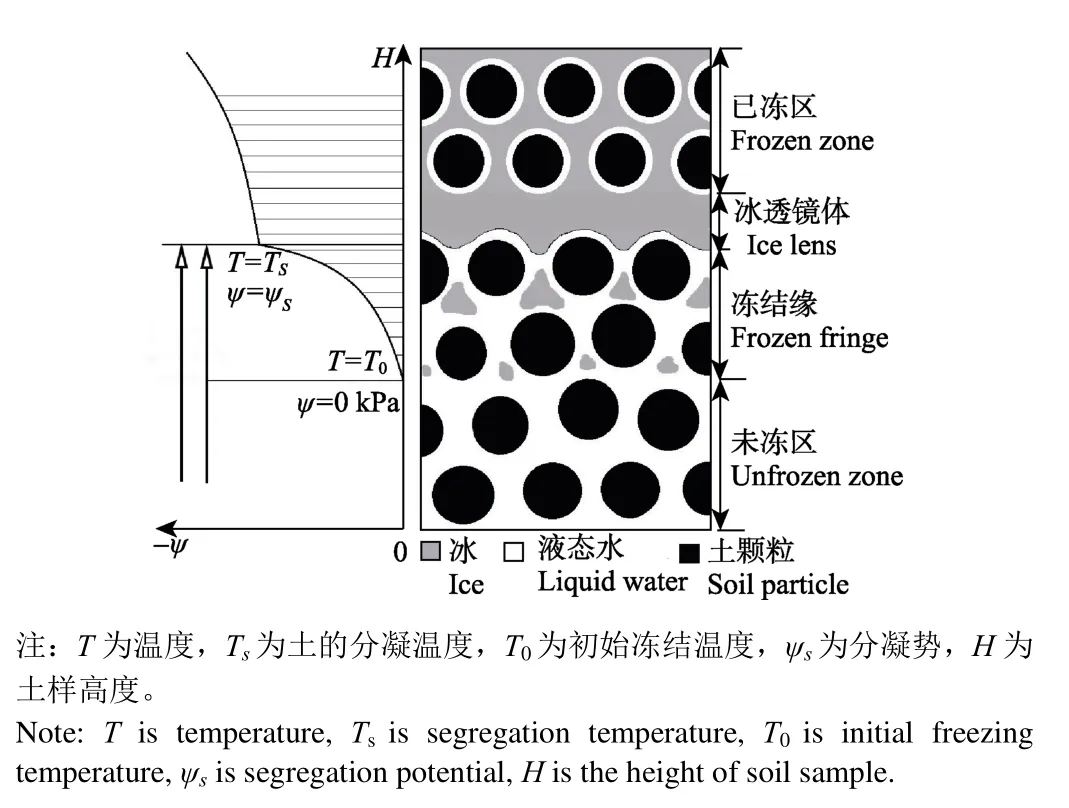
图11 冻结缘附近土体示意图Fig.11 Schematic of soil near frozen fringe

随着温度的进一步降低，冻结锋面继续前进，冻结缘区土体孔隙内液态水继续冻结，水分向分凝冰透镜体迁移越来越困难，迁移速率越来越慢，直到这部分土体完全冻结，下一层分凝冰透镜体形成，水分向上一层冰透镜体的迁移停止。从图11也可以看出，土体各位置基质势达到稳定的时间与液态含水率不再变化的时刻一致，这说明当土体完全冻结，该位置液态含水率不再发生变化后，基质势的值也达到稳定不再变化。同样，与液态水在冻结区的分布一样，完全冻结的土体中不再发生水分迁移，基质势的值也不再变化。这也说明了基质势对于土体中液态水的动态变化具有响应作用。

3 结 论

1）青藏红黏土作为典型的冻胀性敏感土，使用 pF meter基质势传感器以及5TM水分传感器可完整地获得其冻结过程中包括温度、基质势以及水分在内的各物理参数在时间-空间上的动态变化情况。冻结过程中土体温度场的改变引起土孔隙中的液态水相变为冰晶，导致土中不同位置液态水的能量状态发生改变，从而使液态水从高势能区向低势能区发生定向的迁移。试验中土体两端施加的温度梯度决定了土体的冻结速率以及冻结深度的发展程度，也决定了土体中液态水的分布状况，同时，土体温度的变化引起了各位置液态水基质势的差异，这为土体水分的迁移提供了基本条件。

2）土体冻胀可分为3个阶段：第I阶段（0～4 h）内冻胀量较小且不明显，第II阶段（4～60 h）冻胀量迅速增加，此时土体内分凝冰开始生长，水分迁移活动剧烈，第III阶段土体内分凝冰生长趋于稳定，液态水停止迁移。冻胀的发生与水分迁移的快慢以及数量具有线性关系。

3）冻结完成后，冻结区最大含水率高达55 %，靠近冻融交界面处的未冻区含水率减小至25.8 %，土体中的水分整体向上发生了迁移。试验后土体内含水率与分凝冰透镜体的分布一致；土体冻结区液态含水率的分布与温度梯度近似成线性关系，与含水率及水分迁移无关；未冻区液态含水率的分布与水分的迁移量有关，与温度梯度无关。

4）基质势作为冻土水分迁移的驱动因素，对冻结过程中液态水数量变化具有及其运移具有显著的响应作用。冻结前期，已冻区液态含水率减小，冻结锋面下方土体基质势持续为0，20 h时，靠近顶板处土体基质势达到–1 000 kPa左右，土样14、12、10 cm高处分别减小至–55、–47.5、–30.2 kPa。当冻结速率开始减慢，分凝冰开始生长时，液态水向上发生迁移，同时，冻结锋面下方的基质势持续减小，这是由于未冻区液态水向已冻区发生迁移造成，说明水分迁移需要同时满足相邻位置之间的基质势差以及充足的时间这2个条件。

5）试验证明，虽然土体温度场的变化和水分迁移具有因和果的关系，但 2个过程并不同步，当冻结速率减小到一定程度时，土中液态水才开始发生迁移；而当土体温度场趋于稳定时（10 h），水分迁移并未停止，反而因为冻结速率减慢，为大量水分迁移至冻结锋面后方提供了充足的时间保证。

[1]Taber S. Frost heaving[J]. Journal of Geology, 1992, 37(5):428－461.

[2]Taber S. The mechanics of frost heaving[J]. Journal of Geology, 1930, 38(4): 303－317.

[3]王永涛，王大雁，马巍，等. 青藏粉质粘土但向冻结冷生构造发育及冻胀发展过程试验研究[J]. 岩土力学，2016，37(5)：1333－1342.Wang Yongtao, Wang Dayan, Ma Wei, et al. Experimentalstudy of development of cryostructure and frost heave of the Qinghai-Tibet silty clay under one-dimensional freezing[J].Rock and Soil Mechanics, 2016, 37(5)：1333－1342. (in Chinese with English abstract)

[4]Fowler A C. Secondary frost heave in freezing soils[J]. Siam Journal on Applied Mathematics, 1989, 49(4): 991－1008.

[5]Everett D H. The thermodynamics of frost damage to porous solids[J]. Transactions of the Faraday Society, 1961, 57(5):1541－1551.

[6]李广信. 高等土力学[M]. 北京：清华大学出版社，2012：186－193.

[7]曾桂军，张明义，李振萍，等. 饱和正冻土水分迁移及冻胀模型研究[J]. 岩土力学，2015，36(4)：1085－1092.Zeng Guijun, Zhang Mingyi, Li Zhenping, et al. Study of moisture migration and frost heave model of freezing saturated soil[J]. Rock and Soil Mechanics, 2015, 36(4):1085－1092. (in Chinese with English abstract)

[8]白莉，王有镗，高青，等. 地下换热管土结构冻胀变形模拟[J]. 农业工程学报，2016，32(18)：118－124.Bai Li, Wang Youtang, Gao Qing, et al. Simulation on underground pipe-soil heat exchange structure deformation due to frost heave [J]. Transactions of the Chinese Society of Agriculture Engineering(Transactions of the CSAE), 2016,32(18): 118－124. (in Chinese with English abstract)

[9]Nakano Y, Tice A R. Transport of water due to a temperature gradient in unsaturated frozen clay[J]. Cold Regions Science& Technology, 1990, 18(1): 57–75.

[10]Nakano Y, Horiguchi K. Role of heat and water transport in frost heaving of fine-grained porous media under negligible overburden pressure[J]. Advances in Water Resources, 1984,7(2): 93－102.

[11]Bronfenbrener L, Bronfenbrener R. Frost heave and phase front instability in freezing soils[J]. Cold Region Science and Technology, 2010, 64(1): 19－38.

[12]孙后超，杨平，王国良. 冻黏土与结构接触界面层单剪力学特征试验[J]. 农业工程学报，2015，31(9)：57－62.Sun Houchao, Yang Ping, Wang Guoliang. Monotonic shear mechanical characteristics and affecting factors of interface layers between frozen soil and structure [J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2015, 31(9): 57－62. (in Chinese with English abstract)

[13]付强，侯仁杰，王子龙，等. 冻融期积雪覆盖下土壤水热交互效应[J]. 农业工程学报，2015，31(15)：101－107.Fu Qiang, Hou Renjie, Wang Zilong, et al. Soil moisture thermal interaction effects under snow cover during freezing and thawing period[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015,31(15): 101－107. (in Chinese with English abstract)

[14]马巍，王大雁. 冻土力学[M]. 北京：科学出版社，2014：41－56.

[15]徐斅祖，王家澄，张立新，等. 温度梯度诱导薄膜水迁移的冻胀机理[J]. 科学通报, 1997, 42(9): 956－959.Xu Xiaozu, Wang Jiacheng, Zhang Lixin, et al. Frost heaving mechanism of film water migration induced by temperature gradient[J]. Chinese Science Bulletin, 1997, 42(9): 956－959.(in Chinese with English abstract)

[16]Taylor G S, Luthin J N. A model for coupled heat and moisture transfer during soil freezing[J]. Canadian Geotechnical Journal, 2011, 15(4): 548－555.

[17]Sill R C, Skapaki A S. Method for the determination of the surface tension of solids, from their melting points in thin wedges[J]. Journal of Chemical Physics, 1956, 24(4): 644－651.

[18]陈飞熊，宋战平，李宁. 基于吸附薄膜理论的正冻土水分驱动力模型探讨[J]. 水利与建筑工程学报，2006，4(3)：1－4.Chen Feixiong, Song Zhanping, Li Ning. Study on moisture migrating force model of freezing soil base on adsorption-film moisture migration mechanism [J]. Journal of Water Resources and Architectural Engineering, 2006, 4(3):1－4. (in Chinese with English abstract)

[19]Nakano Y, Tice A R, Joseph Oliphant, et al. Transport of water in frozen soil: Experimental determination of soil-water diffusivity under isothermal conditions[J]. Advances in Water Resources, 1983, 5(4): 221－226.

[20]Iwata S. Thermodynamics of soil water: IV. Chemical potential of soil water [J]. Soil Science, 1974, 117(3): 135－139.

[21]徐斅祖，邓友生. 冻土中水分迁移的实验研究[M]. 北京：科学出版社，1991.

[22]明锋. 饱和土冻结过程中冰透镜体生长规律研究[D]. 兰州：中国科学院大学，2014.Ming Feng. Study on the Growth of Ice Lens during Freezing of Saturated Soil[D]. Lanzhou: University of Chinese Academy of Sciences, 2014. (in Chinese with English abstract)

[23]徐斅祖，王家澄，张立新.冻土物理学[M]. 北京：科学出版社，2001：68－74.

[24]Buckingham E. Studies on the movement of soil moisture[J].Diffusion, 1907.

[25]Schofield R K. The pF of water in the soil[J]. Int Congress Soil Sci, 1935, 3: 37－48.

[26]Croney D, Coleman J D, Bridge P M. The suction of moisture held in the soil and other porous materials[M]// The Suction of Moisture Held in Soil and Other Porous Materials.London: Her Majesty’s Stationary office, 1952.

[27]温智，马巍，薛珂，等. 基于pF meter基质势传感器的冻土水分迁移研究[J]. 土壤通报，2014，45(2)：370－375.Wen Zhi, Ma Wei, Xue Ke, et al. Study on moisture migration in frozen soil by soil matric potential sensor[J].Chinese Journal of Soil Science, 2014, 45(2): 370－375. (in Chinese with English abstract)

[28]Wen Zhi, Ma Wei, Feng Wenjie, et al. Experimental study on unfrozen water content and soil matric potential of Qinghai-Tibetan silty clay[J]. Environment Earth Sciences,2012, 66(5): 1467－1476.

[29]Topp G C, Davis J L, Annan A P. Electromagnetic determination of soil water content measurements in coaxial transmissions lines[J]. Water Resource Res, 1980, 16(3): 574－582.

[30]Topp G C, Davis J L, Annan A P. Electromagnetic determination of soil water content using TDR (I).Application of wetting fronts and steep gradients[J]. Soil Science Society of America journal, 1982, 4 (6): 672－678.

[31]薛珂，温智，张明礼，等. 5TM传感器在冻土水热研究中的适用性评价[J]. 工程地质学报，2015，23(增刊)：668－675.Xue Ke, Wen Zhi, Zhang Mingli, et al. The applicability evaluation of 5TM on heat and moisture research in frozen soil[J]. Journal of Engineering Geology, 2015, 23(Suppl.):668－675. (in Chinese with English abstract)

Relationship between matric potential, moisture migration and frost heave in freezing process of soil

Xue Ke1,2, Wen Zhi1※, Zhang Mingli3, Li Desheng1,2, Gao Qiang1,2
(1.State Key Laboratory of Frozen Soil Engineering, Northwest Institute of Eco-Environmental and Resources, Chinese Academy of Sciences, Lanzhou730000, China; 2.University of Chinese Academy of Sciences, Beijing100049,China;3.College of Civil Engineering, Lanzhou University of Technology, Lanzhou730050,China)

The moisture migration from unfrozen region to freezing front is the main factor that causes frost heave during soil freezing, it is generally believed that the energy difference between two positions in soil drives the liquid water migrate to frozen region and leads water redistribution when soil freezing. However, limited by technical means, the matric potential measurement in frozen soil is still an open problem. In this study, the relationship between matric potential, soil water content and frost heave was investigated by using the newly introduced pF meter matric potential sensor and the 5TM water content sensor that could liquid water content and matric potential in one-dimension saturated soil freezing. The results showed the temperature field change caused the change of the liquid pore water phase into the ice, led the destruction of the initial energy equilibrium in different position of the soil sample, and then caused the liquid water migrated from high potential area to a relatively low potential area. During the freezing experiment, we found that the 16-cm depth of the soil sample began to freeze when the experiment had been conducted for 4 hours, and the freezing was from top to deep soil. When the experiment had been conducted for 4 hours, the freezing arrived at 10-cm depth of the soil sample, and the frozen depth kept unchanged. After the experiment，the water content in 10-14 cm of the soil sample could reach as high as about 55%, and at the 6 cm soil sample height, the liquid water content in the unfrozen region reduced to 25.8%, which supported the moisture movement upwards to the upper part of the soil sample. The frost heave process of saturated soil could be divided into 3 stages: 1) In 0-4 h, the frost heave amount was smaller; 2) In 4-60 h, the frost heave amount increased rapidly and the segregation ice began to grow, the moisture migration process were active; 3) The growth of segregation ice tended to stabilize and the liquid water stopped migrating to the freezing front; Similarly, the soil matric potential would have response to the change of the liquid water content and the moisture migration during the freezing process. In the early stage of freezing, the liquid water content in frozen region decreased, and the soil matric potential below the freezing front lasted for 0. When the freezing had been conducted for 20 h, the soil matric potential near the upper cooling plate reached about -1 000 kPa, and the soil matric potential in 14, 12, 10 cm of the soil samples was –55, –47.5, –30.2 kPa, respectively. When the freezing rate slowed down and the segregation ice began to grow, the liquid water tended to migrate upward, meanwhile, the soil matric potential below the freezing front decreased continuously, which were due to the liquid water migration from the unfrozen region to the frozen region. Results supported the moisture migration required 2 conditions: the matric potential difference between 2 positions in soil and the sufficient time. After the experiment, the distribution of the water content in the soil was consistent with that of the segregation ice lens. In the frozen region, the liquid water content was approximately linear with the temperature gradient, and in unfrozen region, the liquid water content was related to the amount of migrated moisture, but not related to the temperature gradient. The results provide an experimental basis for understanding frost heave mechanism and the establishment of frost heave model.

soils; freezing; water content; temperature; frozen heave; segregation ice; matric potential; pF meter

10.11975/j.issn.1002-6819.2017.10.023

TU411.2; S152.7

A

1002-6819(2017)-10-0176-08

2016-10-01

2017-04-11

国家自然科学基金项目（41471061、41690144）；冻土工程国家重点实验室自主课题（SKLFSE-ZT-22）；中科院寒旱所STS项目（HHSTSS-STS-1502）

薛 珂，男，甘肃渭源人，博士生，主要从事冻土物理学与寒区工程研究。兰州 中国科学院西北生态环境资源研究院，730000。

Email：tumuxk@163.com

※通信作者：温 智，男，内蒙古呼和浩特人，研究员，博士生导师，主要从事土力学与寒区工程研究。兰州 中国科学院西北生态环境资源研究院，730000。Email：wenzhi@lzb.ac.cn