基于同性异形演变的羽毛球击球机构运动分析

赵 地,杜玉红,焉台郎,王鹏超

(天津工业大学 机械工程学院,天津 300387)



基于同性异形演变的羽毛球击球机构运动分析

赵 地,杜玉红,焉台郎,王鹏超

(天津工业大学 机械工程学院,天津 300387)

依据羽毛球击球机构原理,从同性异形原则出发得到演变机构,对其运用复数法进行运动分析.结合真实运动建立等效力学模型,并利用仿真输出前后不同角度下的角速度,直观反映了运动规律,分析等效后的运动状态,对比等效前后的角速度,得出结果:等效力学模型击球首末角速度具有良好的对称性,为以后的机构分析与实际结构设计打下基础.

同性异形演变; 等效力学模型; 运动分析; 功能关系

羽毛球机器人作为一种新兴的体育类机器人,在国内外均有一定的发展.国外目前主要以结合视觉、机械手臂等高度机电一体化设备为基础,设计出精度高、灵活度高、稳定性良好的羽毛球机器人,如Universal Robots公司制造的UR5型机器人,可以自主识别羽毛球的运动轨迹,通过计算机预判处理来确定羽毛球的落点,进而控制机械手让球拍运动到落点实现击球.国内机器人主要侧重于机械机构并配以简单的机电传动系统,比如大连理工大学采用通过离合器闭合电机带动击球机构运动完成击球.

本文讨论以气缸为动力源驱动连杆转动的“单级对心气缸平面连杆机构”为羽毛球击球机构的运动分析.运用同性异形演化原理[1]将击球机构与其他结构对比,为寻找类似功能提供一种方法,并列出本机构的运动方程,为以后的机构尺寸设计、气缸选型等改进提供帮助.

1 羽毛球发球击球机构原理与分析

相比力量与速度,羽毛球比赛中竞技技巧更为重要,所以为羽毛球机器人选择合适的机构来完成发球显得尤为重要.本文选择气缸作为动力元件,推动固定有羽毛球的连杆来进行击球,可通过调整不同的气压来对击球的力度进行调整,并通过调整机构各部件尺寸调整击球角度、击球过程的速度和加速度.

羽毛球击球机构是羽毛球机器人的一部分,羽毛球机器人三维图如图1所示.击球过程首先为气缸注入高压气体,活塞杆向前伸出推动球拍,通过球拍绕定轴转动实现击球动作,完成一次击球.为便于分析对模型进行简化,简化图如图2所示.现由图2做出图3的机构运动简图,图2中机架简化为图3中竖直方向上的机架0,推板简化为杆件1,气缸、缸杆分别简化为杆件3和杆件2.气缸与活塞杆组成移动副,两者轴线重合,可视为“长度可伸缩的连杆”,而此机构的动力元件是气缸的活塞,因此从结构的角度上来说,击球机构具有两个特点:①具有可变长度连杆;②动力元件不与机架相连.从特点②可以看出,这种气动连杆机构不符合阿苏尔的分类观点,故不能分为阿苏尔杆组.但从特点①上看,我们可以将气缸假设为一种可伸缩的“特殊”杆件,这样就可以尝试根据阿苏尔杆组分类法,将此Ⅱ级杆组看成一种“单杠Ⅱ级杆组”,则杆组运动分析模型可以运用其上.这是对于有气缸、液压缸的机构的一种运动分析方法.

图1 羽毛球机器人三维图Fig.1 Badminton robot 3D figure

图2 羽毛球机器人击球简化结构Fig.2 Badminton robot simplified structure

图3 机构运动简图Fig.3 Machine movement schematic diagram

2 同性异形的应用与分析

2.1 同性异形的演化应用

同性异形演化作为创新方法之一,虽然它在理论体系全面性和操作性上逊于“再生运动链法”[2-4],但其以简单、实用等优点在实际工程中得到广泛应用[5-10].结构抽象出不同的简图,其运动特性不尽相同,所以对某一机构进行设计时,不仅要考虑机构的构成,还要筛选和演化,再进行运动分析和动力学分析.通过同性异形的演化改进,得到所需机构并实现功能,达到事半功倍的效果.

单级气缸连杆机构的转化主要集中于气缸,从运动特性上看,缸杆与缸体相对运动属于移动副.对一般移动副来说,滑槽为包容面,滑块为被包容面,结合本文机构与实际情况,选取演化原理[1]中的组成低副(移动副、转动副),这两元素的包容面与被包容面可以互换而不影响该副的运动特性同性异形规则.气缸可通过普通移动副的同性异形演化得到.由于包容面与被包容面的互换,气缸的缸体演化为移动副的滑体,而缸杆则成为滑槽,得到同性异形演化机构.羽毛球机器人的击球同性异形演化机构如图4所示.

2.2 演化机构对比分析与延伸

虽然移动副的包容面与被包容面互相调换,在外形上常常有很大的变化,但因方位未变,所以该移动副特性不变.当气缸内注入压缩气体时缸杆迅速推动连杆,做出击球动作,而在演化机构中滑槽充当缸杆的作用,运动特性并不发生改变,这也是同性异形演变的条件之一.

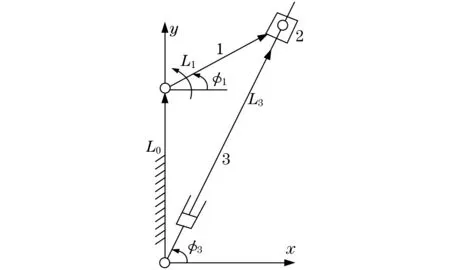
图4 导杆机构Fig.4 Guide rod mechanism

演化的机构为导杆机构,是曲柄滑块机构中的一种,而曲柄滑块机构则是由曲柄连杆机构中的某个转动副由移动副替代而来,从转换与演化上来看,发球击球机构试从曲柄滑块上开始考虑演化.将曲柄连杆中的某转动副变形,形成类似连杆的元素,像凸轮进而成为凸轮连杆机构,在驱动方式上选用电机为动力源,或者成为不同类型的曲柄滑块机构,然后将移动副进一步演化为气缸.

3 基于同性异形的单级气缸连杆机构的运动特性分析

同性异形要求演化前后运动特性不变,所以从演化后机构出发,分析机构特性,再对演化前后机构的相同部分进行进一步列式求解和分析.

单级对心气缸平面连杆机构的运动关系求解,先对演化后导杆机构来进行位移、速度的列式.当气缸为匀速伸出时,可得位置分析如下:

(1)

式中:L0为机架长度;L1为推板长度;L3为缸杆与缸筒的可变长度;φ1为推板与x轴夹角;φ3为缸杆与x轴夹角;i为虚数单位.

在两轴上分解,得到

(2)

速度分析如下

(3)

终化简得到φ1的转角和角速度ω1的表达式:

(4)

式中:ω1为推板角速度.

式中L0,L1为已知参数,对机构的转角和角速度具有影响,根据需要有针对性地调整参数直至达到需要值.φ1,φ3是机构中的某一位置参数,式(4)给出了两者间关系.通过两种机构对比可知,表达式相同,运动特性不变,反映了同性异形演变的正确性.

4 等效力学模型的建立

4.1 等效力学模型基础

对于单自由度机械系统,若驱动构件的运动已知,则其余构件的运动也就由此确定.在研究其运动时,将系统的动力学等效为对一个构件的动力学.为使等效前后运动一致,要将原系统上作用的外力、转矩等折算到该等效构件上,把质量与转动惯量同样折算到该构件上,而这种折算的依据与基础就是功能原理.等效构件的等效质量和转动惯量具有的动能等于原机械系统的总动能,等效构件上作用的等效力或力矩产生的瞬时功率等于原系统的所有外力的瞬时功率之和,把这种作用有等效力或者等效转矩,并具有等效质量或者转动惯量的等效构件称为原系统的等效力学模型.为计算简便,一般选取驱动构件为等效构件,取转动构件为等效构件,则具有等效转动惯量和等效力矩,取移动构件为等效构件,则具有等效质量和等效力.

4.2 模型分析与建立

本文机构中气缸的缸杆为驱动构件,对整个机构列写动能定理,在时间dt所具有的动能为

(5)

式中:m2为推板质量;Ei为构件i所具有的能量;v2为缸杆伸出速度;Ji为构件i的转动惯量;ωi为构件i的角速度.

而所做的功为

dW=F2v2dt

(6)

式中:F2为气压对缸杆初始外力;W为机构所做的功.

dEi=dW

(7)

列式发现缸杆不仅具有移动所产生的动能,也有转动带来的动能,而且转动惯量与气缸伸出距离有关.虽然气缸具有两种运动状态下的能量,但作为等效构件时其运动形式唯一,则具有的能量单一.通过观察气缸运动进行判断,从图3上看,缸杆沿气缸伸出推动杆件1,由于杆件1不可伸长同时绕转动副1做定轴转动,迫使气缸整体绕转动副3发生摆动,产生角速度.通过运动可知,转动是由于移动产生,进而使得具有转动形式的能量.其次由式(6)右侧看出,只有dt气缸内气体对缸杆的合力产生的瞬时功率,形式上只有速度v2,若取转动构件作为等效构件时,需要从式(6)中对dW提取ω2,而式中不含这一项,进而使这种做法不可行,验证其作为等效构件时移动为唯一的运动形式.提取等效质量与等效力,将速度之间的关系表达式带入,可得化简后的表达式:

(8)

式中:me为等效质量;Fe为等效力.

对于缸杆的伸长速度求解,根据将机械系统转换为等效构件前后功能保持不变的原理,外力F2为气压作用在气缸表面产生的作用力与定值摩擦力的合力、外力所做的功等于等效构件的动能变化,进而列写动能定理方程[11],求得气缸的伸出速度:

(9)

式中:l3j为时刻j时缸杆与缸筒的可变长度;l3i为时刻i时缸杆与缸筒的可变长度;v2i为时刻i时缸杆的伸出速度;v2j为时刻j时缸杆的伸出速度.

5 程序框图与运动求解

5.1 程序框图

编写羽毛球机器人击球速度、角度相应程序,程序流程图如图5所示.

5.2 运动仿真求解与结果分析

将结构参数L0=0.308 m,L1=0.064 m,L3=0.25 m,v0=0.4 m·s-1,F2=80 N,J1=0.1,J3=0.12,m2=6带入式(4),(9)分别求解.

由于运动量之间关系形式不明确,即速度、加速度与时间关系不明以及直接计算运算难度较大等问题,故将数据离散化,采用对气缸伸出距离等步长分解的计算方法求解.根据羽毛球击球高度与距离的要求(至少要将羽毛球击球过网并落入规则要求区域),计算得到角速度至少要大于14°/s,以此为界,以杆件1的角速度为纵坐标,以角度φ3为横坐标作图,并计算相关量得到图6～9.

图5 程序流程图Fig.5 Program flow chart

图6 角速度变化Fig.6 Angular velocity change

图7 伸出距离与速度关系图Fig.7 Chart of reachable distance and velocity

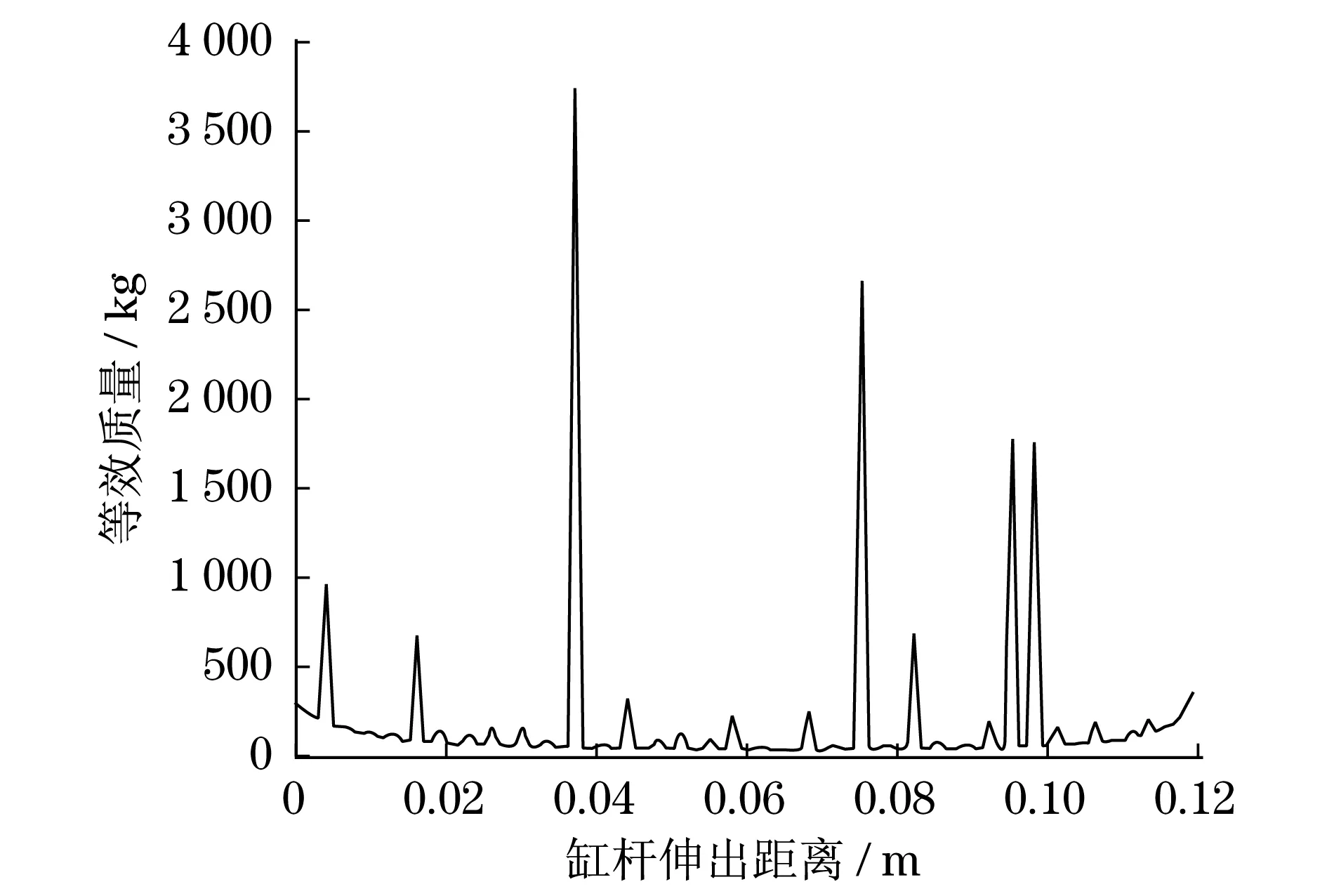
图8 伸出距离与等效质量关系图Fig.8 Chart of reachable distance and equivalent mass

图9 伸出距离与加速度关系图Fig.9 Chart of reachable distance and acceleration

从角速度变化图6中可以看出,随着时间的推移,角速度和角度φ3经历了先减小后增大的过程,杆件1垂直于缸杆2时,角度φ3时度最小,同时对应的角速度也最小,此为拐点位置.在此位置前后角度均大于此时位置对应角度,角速度增大.图中只有水平线以上,为击球合格位置.单纯机构分析在运动刚开始时的约86.7°转到84.5°,以及转动到81.5°并到84.4°时,击球达到要求,而在真实情况下的速度可以从开始的86.7°转到81.2°,并由此起对称的转动直至结束.两者相比真实情况下的速度曲线在转动首末的对称性远好于理想机构分析时的曲线,这便于我们下一步的课题分析,且对现实中调整角度、位置更具有指导意义.

从气缸的伸出距离与速度关系图7可以看出:气缸伸出速度存在一定波动,对实际机构运作存在影响,直接影响整个系统的速度变化.

图8和图9两张图等效质量与等效构件上的加速度波动很大,从公式形式上看,长度比值位于分母上,并以平方扩大其影响,数量级可以达到上百甚至千位.为减小等效质量与加速度波动,尝试从增大杆件尺寸入手,达到减缓效果,而且如果杆件长度趋于无穷大时,其运动形式只有移动形式,不存在转动,等效质量只等于驱动构件本身,气缸摆动角速度约为0,最终不存在波动,进而使得速度、加速度等量的波动极小.能量形式唯一确定,只存在移动的动能,可以得出直线驱动运动中的存在摆动对此构件的影响极大.所以这种既存在转动又存在移动的驱动构件是不推荐的.进一步考虑对于其他一般的机构的从动件受力而产生两种形式的运动,其速度增量变化也会是不小的.

在实际情况中只有在合适的角度上才能完成理想的击球,而由图6可知,击球区较小,可调整的击球角度范围较小,使击球较为困难.为解决此问题,可以调整结构参数,或更换气缸以及调整气缸压力,形成一个在理想击球角度内击球有力而又在击球区域内的理想结构.

6 结论

本文通过同性异形演变将击球机构的单级气缸连杆机构演变为普通的导杆机构,从平面四连杆机构出发,得到凸轮连杆机构尝试作为击球机构.对演变后的摆动导杆机构做了运动分析,建立了等效力学模型,并求解得到所需位置的转角与角速度的公式.仿真得到角位移与角速度的图像,发现目前运动方式存在较大问题,且理想击球范围较小,需要通过调整参数实现更好的击球.此分析为以后的改进与分析打下基础.

[1] 华大年.同性异形机构[J].中国纺织大学学报,1992,18(5):91-97.

HUA D N.Isomeric mechanisms with same kinematics[J].Journal of China Textile University,1992,18(5):91- 97.

[2] YAN H S.A methodology for creative mechanism design[J].Mechanism and Machine Theory,1992,27(3):235-242

[3] YAN H S,CHEN J J.Creative design of a wheel damping mechanism[J].Mechanism and Machine Theory,1985,20(6):597-600.

[4] 颜鸿森.颜氏创造性机构设计(一):设计方法[J].机械设计,1995,12(10):39-41.

YAN H S.Yanshi creative mechanism design(1):design method[J].Journal of Machine Design,1995,12(10):39-41.

[5] 张春林,姚九成.平动齿轮机构的基本型与其演化的研究[J].机械设计与研究,1998(3):26-27.

ZHANG C L,YAO J C.A study of the basic pattern and its evolution of the parallel move gear mechanism[J].Machine Design & Research,1998(3):26-27.

[6] 张春林,荣辉,黄祖德.少齿差行星传动同型异性机构[J].北京理工大学学报,1997,17(1):45-49.

ZHANG C L,RONG H,HUANG Z D.A study of the isomorphic mechanism with distinct properties made up of a planetary gear train with a small tooth difference[J].Journal of Beijing Institute of Technology,1997,17(1):45-49.

[7] 张春林,胡荣晖,姚九成.平动齿轮机构的同性变异法[J].机械设计,1997(7):29-30.

ZHANG C L,HU R H,YAO J C.Translation gear mechanism homosexual variation method[J].Journal of Machine Design,1997(7):29-30.

[8] 常勇.按行程速比系数K设计转动导杆(导块)机构的解析法[J].机械科学与技术,2002,21(3):416-417.

CHANG Y.An analytical method for desiging rotating guiding-rod(guiding-slider)mechanism in accordance with travel velocit-ratio coefficientK[J].Mechanical Science and Technology for Aerospace Engineering,2002,21(3):416-417.

[9] 何晓玲,于文武,刘铁成.移动副的同性演化在机构运动分析中的应用[J].洛阳工学院学报,1998,19(3):36-39.

HE X L,YU W W,LIU T C.Application of the transformation with same kinematics for prismatic pair in mechanism motion analysis[J].Journal of Luoyang Institute of Technology,1998,19(3):36-39.

[10] 郑甲红,冯丽萍.同性异形机构及其应用[J].现代制造工程,2002(9):89-91.

ZHENG J H,FENG L P.Evolution and application of different model mechanisms with the same motion properties[J].Modern Manufacturing Engineering,2002(9):89-91.

[11] 刘艳春,李建军.质点系动能定理应用解析[J].陕西师范大学学报(自然科学版),2005,33:16-17.

LIU Y C,LI J J.Application of kinetic energy theorem of mass point system[J].Journal of Shanxi Normal University:Science and Technology,2005,33:16-17.

Motion-reversion-based motional analysis on badminton batting mechanism

ZHAO Di,DU Yuhong,YAN Tailang,WANG Pengchao

(School of Mechanical Engineering,Tianjin Polytechnic University,Tianjin 300387,China)

According to badminton batting principle,an evolutionary mechanism via motion reversion is proposed using complex-number for motional analysis.In combination with actual motions,an equivalent mechanical model is established. By using the angular velocity with various angles,the movement laws are intuitively reflected.With comparison of motional states,the good symmetry is detected between the initial and last batting angular velocities.Accordingly,this approach sets a basis on mechanism analysis and structural design.

motion reversion； equivalent mechanical model； motional analysis; functional relationship

国家重点基础研究发展计划(973预)资助项目(2010CB334711);国家自然科学基金资助项目(51205288);国家级大学生创新创业训练计划资助项目(201510058053).

赵 地(1985-),男,助教,硕士.E-mail:1345389794@qq.com

TH 122

A

1672-5581(2017)01-0021-06