仿人机器人越障步态控制研究

杜玉红,李 兴,赵 地,杨 朔,常 运

(1.天津工业大学 机械工程学院,天津 300387;2.天津工业大学 天津市现代机电装备技术重点实验室,天津 300387)



仿人机器人越障步态控制研究

杜玉红1,2,李 兴1,2,赵 地1,2,杨 朔1,2,常 运1,2

(1.天津工业大学 机械工程学院,天津 300387;2.天津工业大学 天津市现代机电装备技术重点实验室,天津 300387)

为了解决仿人机器人在复杂路面的行走问题,提出了一种具有几何约束的机器人越障过程步态规划方法.首先建立其运动学模型,然后分析各个关键阶段机器人的姿态,计算出各关键姿态关节角度的变化,从而规划出机器人越障的整个过程.运用三次样条插值的方法使得各个关键姿态之间各关节运动平滑稳定,并根据规划中的各个运动过程利用MATLAB仿真,获得机器人在越障过程中各个关节的运动轨迹,并通过试验验证,对整个过程中力值以及压力中心进行实时检测,证明在整个越障过程中机器人的压力中心始终落在其双脚支撑区域,从而说明试验方法的正确性.

仿人机器人; 步态规划; 越障

21世纪以来,人们对仿人机器人具有很高的期望,在仿人机器人的运动领域中,能够实现仿人机器人能像人一样稳定地行走是其技术关键.然而人们对仿人机器人步态的研究一直集中在平地行走上,实际行走路面具有其复杂性,前方遇到障碍物也是一种常见的情况,因此规划出一种稳定有效的越障方案至关重要,是仿人机器人实现复杂路面行走的关键一步.

仿人机器人相对于轮式、履带式等机器人的优越性也是由于其双足的灵活性,譬如上下楼梯、越障等.对于这些复杂路面的步态规划,多数研究学者采用离线规划与实时调整的方式得到期望的关节轨迹.HUANG等[1]通过对髋关节点在单腿支撑期内的两个参数调整来保持稳定性.KAJITA等[2]运用桌子-小车模型来分析ZMP与CPG之间的关系以实现对仿人机器人的步行控制.而HELIOT等[3]通过模拟人类中央神经系统(CNS)的特点,提出了一种通过非线性振荡器来实现机器人和外部传感器之间实现同步步行的策略.本文通过对障碍物高度以及仿人机器人各关节的信息,根据人越障的形态,对仿人机器人进行模仿定位;然后运用逆运动学对各关节角度进行计算,并通过调整支撑腿踝关节、髋关节以及通过手臂关节的位置来约束质心范围;最后运用三次多项式插值的方法对各关节进行运动规划,使机器人能够平稳地越过障碍物,同时也缓解机器人在跨越过程中所产生的惯性力影响.

1 仿人机器人正运动学模型

1.1 变换矩阵的建立

本文以GP2013仿人机器人为研究对象.在研究机器人运动学过程中,首先要建立机器人各构件的坐标系,从而得出机器人齐次坐标变换矩阵Ai.并且,只要坐标原点在关节转动轴上,局部坐标系可设在任何需要的地方,然而该机器人踝关节处两轴交于一点,将他们的局部坐标系原点都设定在该交点上是个合理的选择.设定的局部坐标系如图1所示.

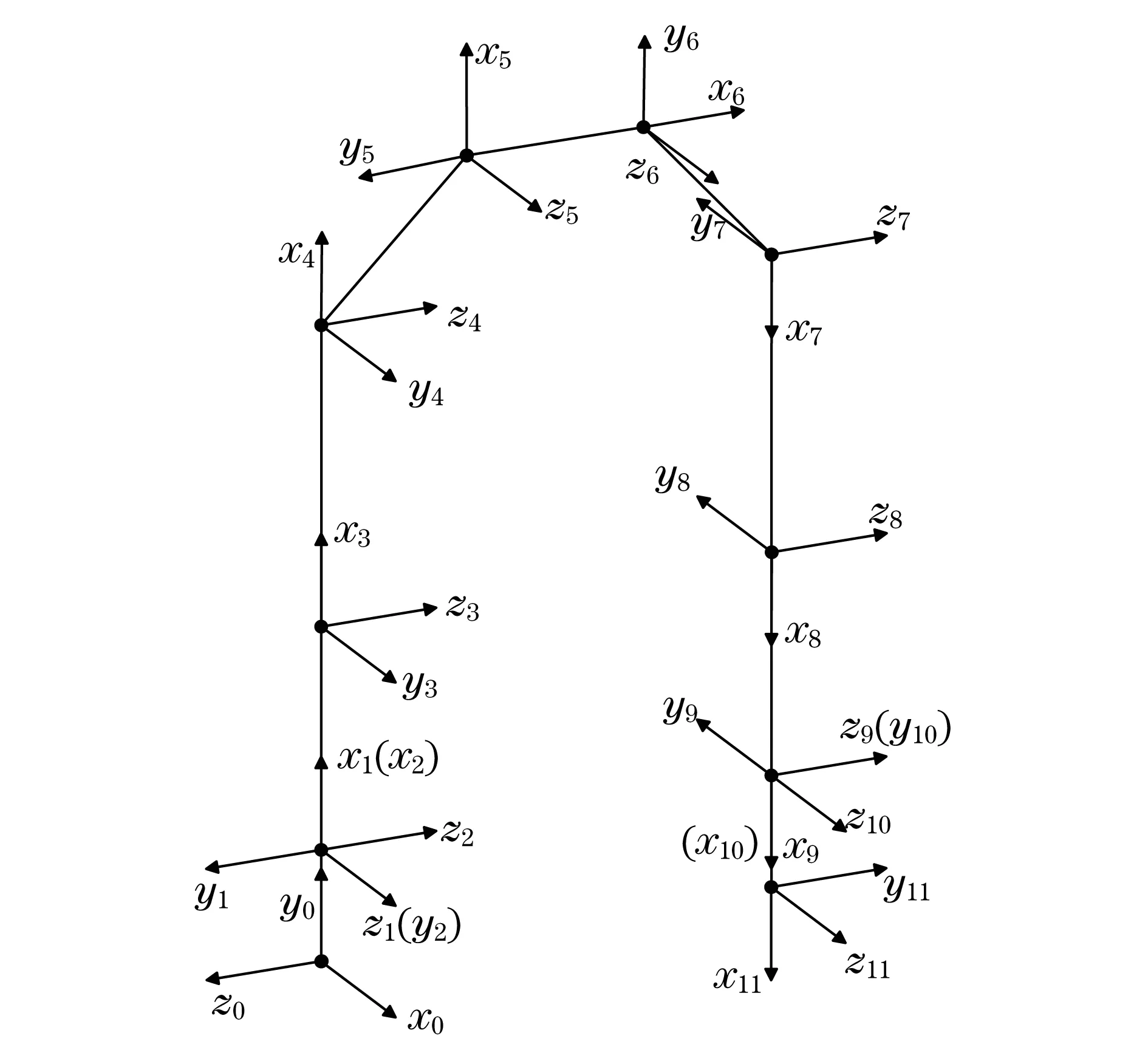
图1 机器人下肢坐标系图Fig.1 Robot lower limb coordinate system

根据Denavit-Hartenberg运动学表示法,如图1的连杆坐标系可用4个参数来描述.对于仿人机器人来说,各关节均为转动关节,所以连杆夹角θi是关节变量,而连杆长度ai、连杆扭角αi、连杆距离di均为固定值.

由连杆坐标系间变换矩阵可知,从连杆i到连杆(i-1)的变换矩阵Ai为

(1)

1.2 D-H坐标法的局限性以及运动方程的建立

虽然D-H坐标法已被广泛应用于机器人的运动学建模,但是D-H坐标法仍不能针对所有关节连杆进行建模[7].以此仿人机器人为例,由于基于D-H坐标的运动只限于x轴和z轴,并不能表达y轴的运动,所以在连杆8到连杆7的坐标变换不能直接带入坐标变换矩阵Ai中,其坐标变换应为

(2)

所以,由上可知,机器人的运动方程为T11=A1A2A3A4A5A6A7A8A9A10A11,即机器人左脚脚掌中心坐标系相对于右脚脚掌中心坐标系的其次变换矩阵为T11.并且,根据上述坐标变换矩阵,可以得出仿人机器人左脚脚掌中心坐标系相对于连杆(i-1)坐标系的齐次变换矩阵为i-1T11=AiAi+1...A11.

然而,在机器人实际步态规划当中,需要将机器人的前向运动和侧向运动分开考虑,由于越障过程中侧向运动只与调节平衡有关,所以只需考虑前向运动即可.在前向运动中用到了关节(2,3,4,7,8,9)6个关节,并根据MATLAB中RoboticsToolbox工具箱建立其前向运动学模型,如图2所示.

2 仿人机器人逆运动学的计算

在仿人机器人行走的过程当中,其运动学逆解具有多解性,对于给定的位置与姿态,它可能具有不同的解,究其原因就是由于解反三角函数方程产生的.

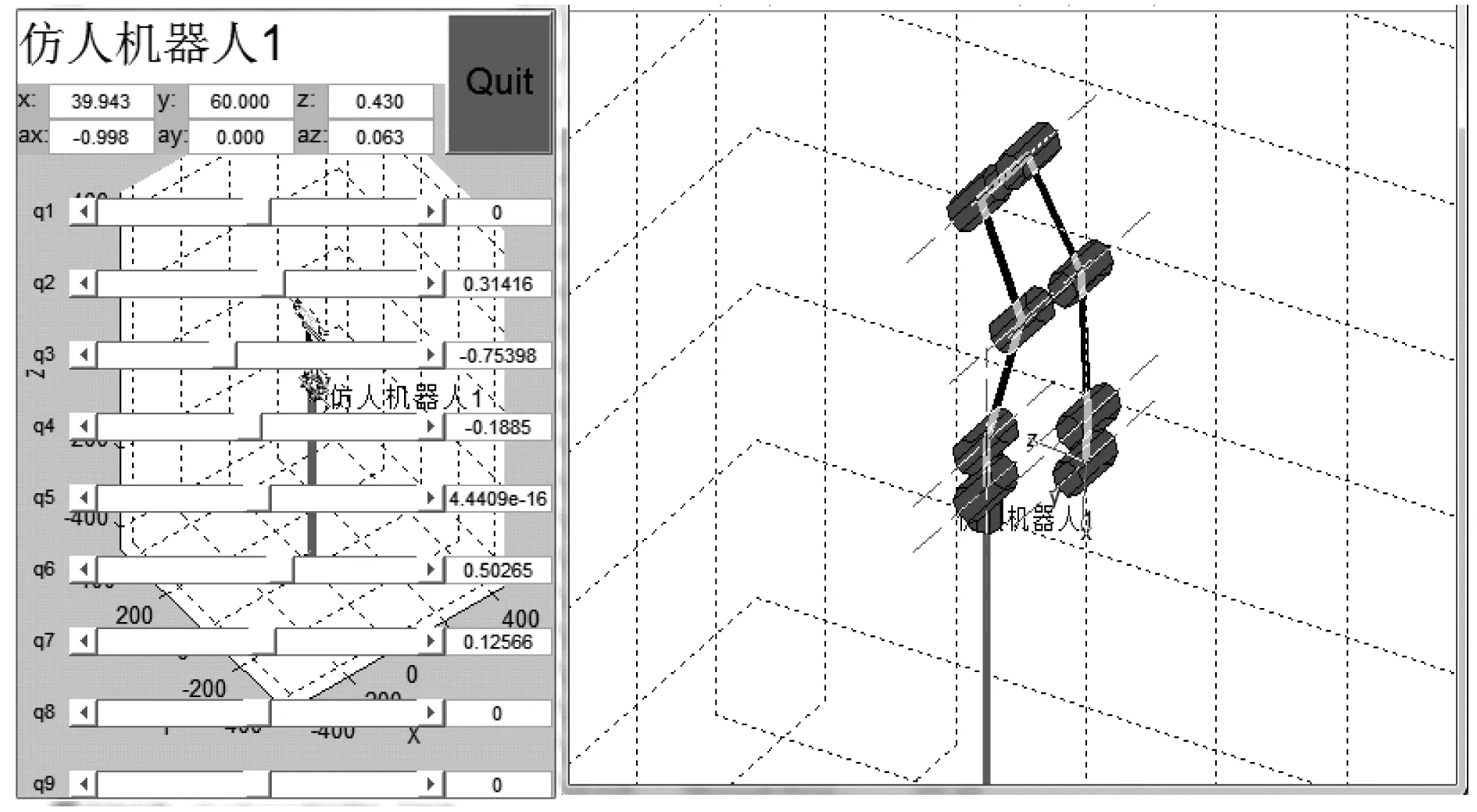
图2 仿人机器人前向关节运动学模型Fig.2 Kinematics model of humanoid robot forward joint

在规划仿人机器人步态的过程中,不考虑髋关节的侧向运动,根据给出机器人模型的左腿,给定腰部中心、左腿骨宽关节及踝关节位姿(pα,Rα,p7,R7),(p10,R10).为了方便函数的计算,定义腰部中心到髋关节距离为D (30mm),大腿长A (76mm),小腿长B (90mm),如图3a所示.则髋关节的位置为

(3)

式中:pα为左腿骨宽关节∑w中的位置;Rα为左腿位骨宽关节转动的3*3矩阵.

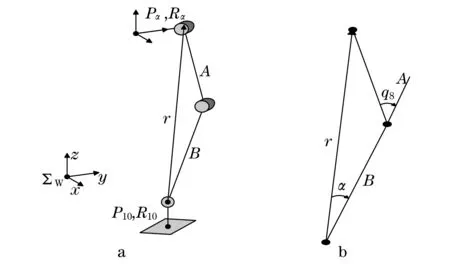
图3 左腿关节符号的定义以及膝关节角的计算Fig.3 Definition of left leg，s joint symbol and calculation of knee joint angle

而在踝关节坐标系中的髋关节位置矢量为

(4)

式中：rx，ry，rz分别为骨宽关节在踝关节坐标系X,Y,Z的坐标值.

从而求得踝关节与髋关节之间的距离C:

(5)

根据余弦定理得膝关节角度q8为

(6)

记三角形下端角为α,根据正弦定理得

(7)

考虑踝关节坐标系,如图4所示,根据矢量r可以求得踝关节的滚动角q10与俯仰角q9分别为

(8)

(9)

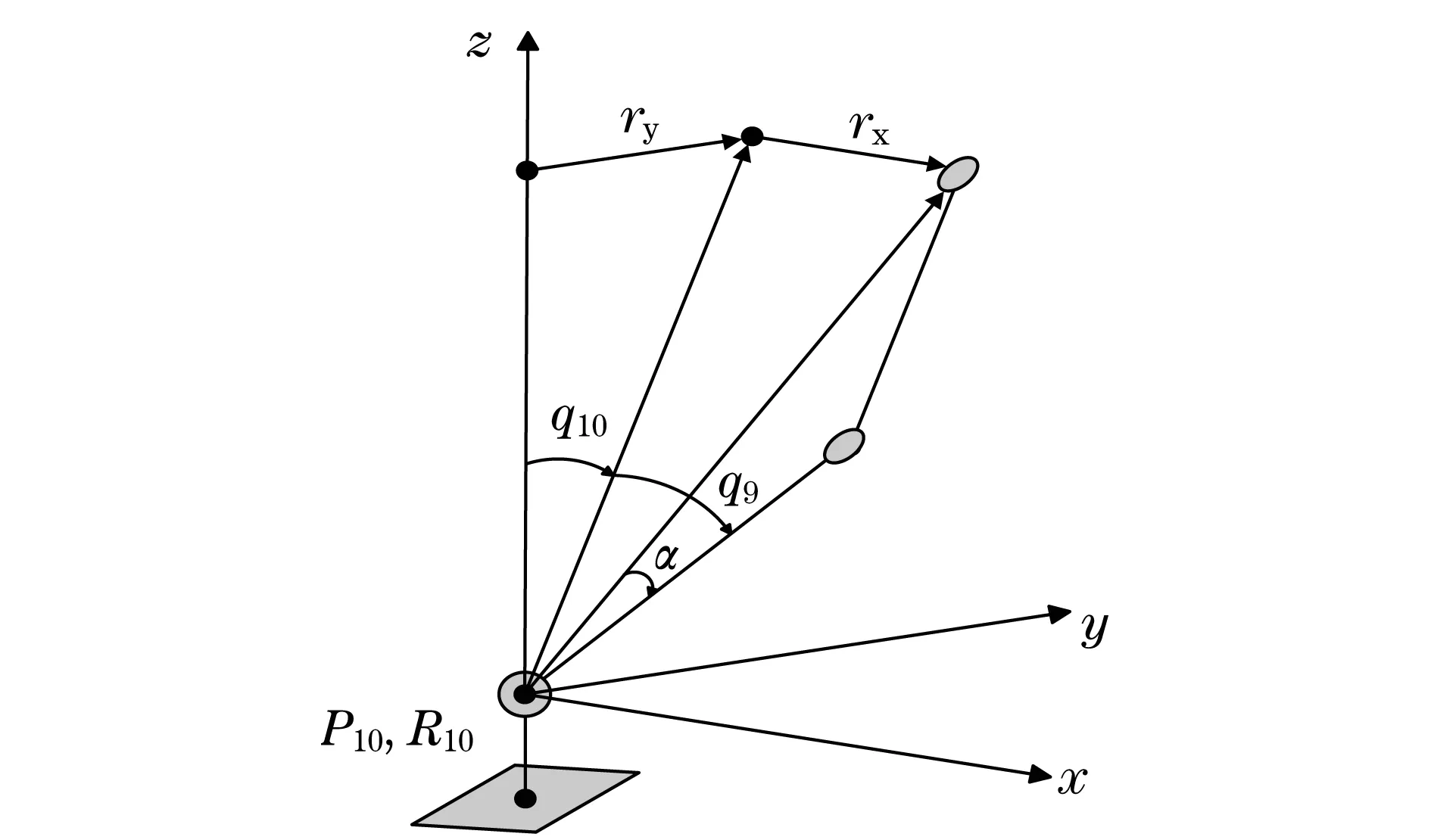
图4 踝关节角的计算Fig.4 Calculation of ankle joint angle

最后求髋关节角度,各连杆之间的关系为

(10)

式中:Ry(θ)表示绕Y轴转动的俯仰矩阵.

对式(10)进行变形可得

(11)

展开计算左右两边得

(12)

进而得出骨宽关节角度q7为

(13)

3 机器人的越障规划及试验验证

3.1 仿人机器人各关节角度变化

在规划的过程中,以人迈过高度位于膝盖位置的障碍物为研究对象,对仿人机器人进行模拟.选取关键位置:右腿抬起位置、右腿前伸位置、右腿落地位置、左腿抬起位置.利用“本文2仿人机器人道运动学的计算”所述方法,计算出各关键位置机器人各个运动关节的转角.

由于人体模型与仿人机器人模型存在差异,质心位置必然有所不同,所以根据第3章所述内容调整质心位置,以达到最优结果.仿真结果固定为16 s,各个过程所经历时间如下:

左右腿的关节仿真如图5所示,其中θ9为右腿髋关节角度,在右跨的过程中变化范围大,即2.596～3.992 s时间段;θ13为右腿膝关节角度,在0.992～3.88 s时间段内,θ13变化上下起伏较大,即说明右腿在迈出过程中屈膝以及伸张的过程,其后在4.992 s处伸张达到最大值,即质心越过障碍转移到右脚;θ17的起始变化在于右腿抬起的过程中,使得质心不至于立刻转移到左脚,右脚掌继续起到支撑作用.在5.272 s后,右腿关节参数趋于稳定,只在调整质心当中有微小变化.

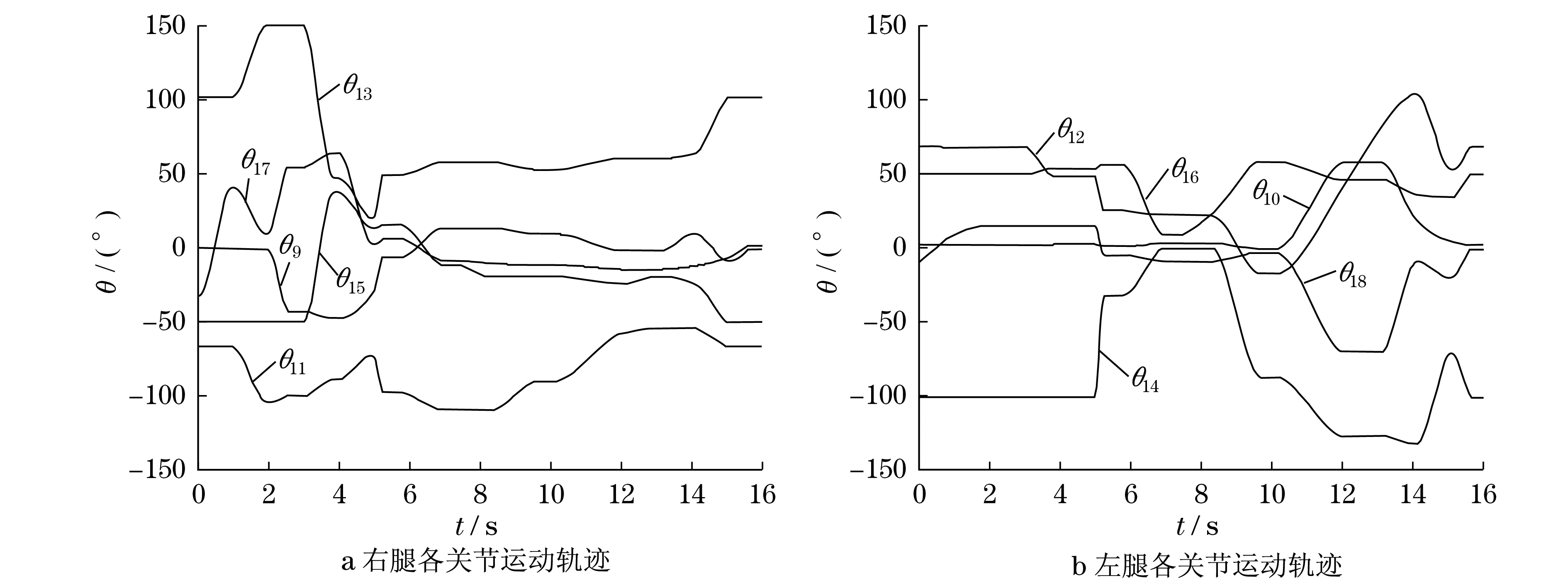
图5 左右腿各关节轨迹Fig.5 Joint trajectory of left and right legs

在右腿抬起落下的过程中,即t=5.272 s前,左腿各关节微调,使质心逐渐趋向左脚脚掌.t=5.272 s之后右脚着地,为缓解落地所产生出的震动以及落地惯性,仿人机器人停止0.48 s.在t=5.752 s后,左腿缓慢向前伸,调整左腿膝关节,使质心逐渐向右脚脚偏移,微调到t=8.312 s后,通过调节左腿髋关节θ12以及膝关节θ14使左腿完全抬起,并在左腿前迈的过程中,为使左脚掌远离障碍物,调整踝关节θ18使左脚掌与地面平行.

手臂关节的调整主要用于使质心尽量靠近脚掌中心位置,在此省略说明.

3.2 足部力值分析以及压力中心验证

整个仿人机器人在越障过程中,舵机加速度对肢体的惯性力会使机器人对地面作用力增强,而在迅速单脚着地以及右腿跨过障碍物时力值波动更大.如图6a,其中上曲线为竖直方向所受作用力,下曲线为左右所受摩擦力.在右脚抬起时刻,即第一个波峰处,作用力增强;而在右腿跨过障碍物未着地时进入波谷,作用力迅速减弱;在右脚接触到地面时,冲击力迅速达到最大值,右腿迈过障碍物到着地的短时间内是作用力变化最大的时候;之后双脚着地,作用力回到初始值.左腿迈过障碍物与之类似,但左腿着地时较平稳,没有冲击力.水平受力也较平稳,由于右脚向前落地时产生摩擦,所以波动较大.

图6 六维测力平台检测分析Fig.6 Analysis and measurement of six dimension force platform

仿人机器人压力中心是对其平稳性判定的重要指标,压力中心始终位于两足以及两足之间所围矩形则说明机器人在稳定阶段.利用六维测力平台可以实时检测出仿人机器人相对平台压力中心的位置,如图6b,曲线交汇位置多则说明压力中心在此位置重合时间最多,如图6b中的a～e5点,其中c点处为右腿跨过后压力中心的集中点.压力中心始终位于双脚所组成支撑区域,则表示质心也处于此区域,则仿人机器人处于稳定状态.

4 结论

通过分析机器人的整体结构,建立机器人下肢运动学模型,并针对D-H法的不足加以修正.将机器人越障的过程分为6个关键状态,然后利用本文所述逆运动学方法求出各个关键状态下的各关节角,并用几何法对机器人越障的各关键状态进行规划,使机器人在越障的过程中保持静态稳定.最后利用三次多项式插值的方法对机器人各关节的具体运动进行规划,并用MATLAB得到光滑的各关节运动轨迹.通过试验验证,对整个过程中力值以及压力中心进行实时检测,证明在整个越障过程中机器人的质心始终落在其双脚支撑区域,从而说明试验方法的正确性.

[1] HUANG Q,YOKOI K,KAJITA S,et al.Planning walking patterns for a biped robot.[J].IEEE Transactions on Robotics,2001,17(3):280-289.

[2] KAJITA S,KANEHIRO F,KANEKO K,et al.Biped walking pattern generation by using preview control of zero-moment point[C]// Proceedings of the IEEE International Conference on Robotics and Automation,Piscataway:IEEE,2003:1620-1626.

[3] CHEVAL L C,AOUSTIN Y.Optimal reference trajectories for walking and running of a biped robot[M].Cambridge:Cambridge University Press,2001:557-569.

[4] SICILIANO B,KHATIB O.机器人手册[M].北京:机械工业出版社,2013.

SICILIANO B,KHATIB O.Robot manual[M].Beijing:China Machine Press,2013.

[5] 王罡.关于双足机器人步态规划方法的研究[J].漳州师范学院学报(自然科学版)2011(4):40-46.

WANG G.Research on gait planning of biped robot[J].Journal of Zhangzhou Normal University:Natural Science Edition,2011(4):40-46.

[6] WANG B,DU Y Q,SUN X Y,et al.Study of humanoid robot gait based on human walking captured data[C]// Proceedings of the 2015 34th Chinese Control Conference,Piscataway:IEEE,2015:4480-4485.

[7] 郭发勇,梅涛,赵江海.D-H法建立连杆坐标系存在的问题及改进[J].中国机械工程,2014,20:2710-2714.

GUO F Y,MEI T,ZHAO J H.Problems and improvement of D-H method for establishing connecting rod coordinate system[J].China Mechanical Engineering,2014,20:2710-2714.

[8] WANG F,LIU Y,LIU J,et al.The stepping balance control strategy for humanoid robot based on capture point theory[C]// Conference on Industrial Electronics and Applications,Piscataway:IEEE, 2015:1426-1431.

[9] WANG L Q,SHANG W W.A gait pattern planning algorithm based on linear coupled oscillator model for humanoid robots.[J].Journal of University of Science and Technology of China,2014,44(10):795-803.

[10] 朱志斌,王岩,陈兴林.一种双足机器人实时步态规划方法及相关数值算法[J].机器人,2008,30(6):521-527.

ZHU Z B， WANG Y,CHEN X L.A realtime gait programming method for biped robot and its related numerical algorithm[J].Robot,2008,30(6):521-527.

[11] 许艳惠.一种双足机器人的步态规划研究[J].核电子学与探测技术,2010,30(4):542-545.

XU Y H.The study of the gait planning of a biped robot[J].Nuclear Electronics & Detection Technology,2010,30(4):542-545.

[12] MOUSAVI P N,BAGHERI A.Mathematical simulation of a seven link biped robot on various surfaces and ZMP considerations[J].Applied Mathematical Modelling,2007,31(1):18-37.

Gait control on humanoid obstacle-crossing robots

DU Yuhong1,2,LI Xing1,2,ZHAO Di1,2,YANG Shuo1,2,CHANG Yun1,2

(1.College of Mechanical Engineering,Tianjin Polytechnic University,Tianjin 300387,China ; 2.Tianjin Key Laboratory of AdvancedMechatronics Electrical Equipment Technology,Tianjin Polytechnic University,Tianjin 300387,China)

In order to resolve the walking problem of humanoid robot on complex pavement,a gait planning method is proposed for humanoid obstacle-crossing robots with geometric constraints. Firstly,the kinematic model is established.Then, the posture of the robot in key stages is analyzed.Next,the key posture joint angle changes are used to plan the whole process.By applying the three-spline interpolation method,the smoothness and stability of joint motions are attained.According to the motional process planning using MATLAB simulation,the motion track during obstacle-crossing is obtained.Finally,it is proven from experimental results that,when the robot crosses obstacles,the pressure center is focused on support-side foot.Therefore,the correctness of the proposed method is verified.

humanoid robot; gait planning; obstacle crossing

国家自然科学青年基金项目(51205288);国家重点基础研究发展计划(973预)资助项目(2010CB334711);国家级大学生创新创业训练计划资助项目(201510058053)

杜玉红(1974-),女,副教授,博士.E-mail:13752153077@163.com

TP 242.6

A

1672-5581(2017)01-0010-05