平动点双脉冲转移轨道的快速计算方法

潘 迅，杨 瑞，泮斌峰，唐 硕

(1. 西北工业大学航天学院，西安710072；2. 航天飞行动力学技术重点实验室，西安710072)



平动点双脉冲转移轨道的快速计算方法

潘 迅1,2，杨 瑞1,2，泮斌峰1,2，唐 硕1

(1. 西北工业大学航天学院，西安710072；2. 航天飞行动力学技术重点实验室，西安710072)

针对限制性三体问题中的平动点双脉冲转移，提出一种高效的计算方法。通过利用基于二维插值的数值流形近似方法对流形进行近似计算，同时利用二体模型下的圆锥曲线近似流形拼接段，根据经典轨道要素推导得到完成拼接所需的速度增量，避免在优化过程中对流形的重复积分计算，以及在三体模型下对拼接段的迭代计算，从而显著提高计算效率。然后推导得到三体问题下的主矢量理论，可将其用于对优化所得的双脉冲转移轨道进行燃料最优性的验证。最后，以航天器从近地圆轨道到地月系L1点的halo轨道的双脉冲转移为例进行数值仿真，验证数值流形近似算法和二体模型近似脉冲的有效性，并表明该方法在优化过程中具有高效性。

圆限制性三体问题；平动点；不变流形近似；主矢量理论；轨道优化；地月转移

0 引 言

随着嫦娥计划的进行，我国的月球探测正在有条不紊的推进过程中。相比于传统的二体模型，圆限制性三体问题模型能更精确地描述地月空间，且存在平动点、周期轨道等众多动力学特性。月球附近存在两个平动点L1点和L2点，前者位于地月之间，可作为地月转移的中转站，后者位于地月连线的延长线上，可对地球和月球背面的连续不间断通信提供支持[1]，也可作为深空探测的基站，对这两个平动点的合理利用有利于后续深空探测的开展。文献[2-4]对平动点附近的空间结构，动力学特性及其在深空探测中应用进行了详细的介绍。 2010年ARTEMIS任务的P1和P2航天器分别进入了地月L2点和地月L1点的拟周期轨道，成为世界上第一次地月平动点任务[5]。我国的嫦娥五号试验器也于2014年对地月系L2点进行了探测。

脉冲推进作为目前的主要推进方式，短期内在实际任务的开展和应用中的地位不可动摇。对于航天器从地球到平动点的脉冲转移轨道的优化设计，目前有较为丰富的研究成果。文献[6]利用三体Lambert问题的迭代算法，对地球到平动点周期轨道的双脉冲转移进行了相关研究；文献[7]结合网格搜索算法和遗传算法对地月系平动点转移轨道的双脉冲转移进行优化；文献[8]利用同构映射将平面圆限制性三体问题的维度从4维降为3维，然后运用几何方法对地球到平动点的转移轨道进行优化；文献[9]基于扰动流形和轨道角动量对地月系平面限制性三体问题的地球停泊轨道和地月L1点之间的多脉冲转移轨道进行设计；文献[10]利用限制性三体问题的动力学系统理论研究了从地球到地月系L3点halo轨道的双脉冲转移；文献[11]对地月系下双脉冲转移进行了详细研究，并对不同流形拼接点和不同halo轨道的转移进行了对比分析；此外，文献[12]针对在日地系和地月系耦合双三体模型下的脉冲转移进行了研究。

在三体模型下对平动点转移轨道进行设计时，为节省能量，均利用了稳定不变流形能无动力趋向于周期轨道的特性。不变流形可通过对流形初始点进行数值积分得到。在优化过程中，需要对从近地停泊轨道进入流形的位置进行优化，即选取合适的流形拼接点。在优化过程中需要多次积分得到不同的流形状态点作为拼接点，计算量较大，增加了优化难度。文献[13]提出了数值流形近似计算方法，先利用二维三次卷积插值得到流形近似值，然后根据能量对其进行修正，得到更为精确的流形状态点，避免了重复积分过程；文献[14]也对该流形近似计算方法进行了研究，并将其应用于基于形状法的低能转移轨道。

在得到脉冲转移轨道后，需要对该轨道的最优性进行验证。Lawden[15]在1963年提出二体动力学的主矢量理论，可用于确定是否为最优飞行轨道。文献[16]对三体问题下的月地返回轨道进行优化，并利用主矢量理论验证了其优化结果的最优性。

本文对地月系圆限制性三体问题下的平动点双脉冲转移轨道进行研究。对于近地停泊轨道与不变流形的拼接段，以二体模型下的圆锥曲线进行近似，得到优化结果后再进行修正，减小对拼接段脉冲的优化难度及优化时间，同时结合数值流形近似计算方法，缩短了优化时间。与文献中的研究相比，采用本文的方法能在极短时间内得到优化结果，显著提高优化效率，并经主矢量理论验证，优化结果为最优脉冲转移轨道。

1 限制性三体问题

对于地月系圆限制性三体问题，航天器在转移过程中同时受到两个主天体地球和月球的影响，其在旋转坐标系中的动力学模型为

(1)

式中：μ表示主天体的质量比，是三体系统的唯一参数，在地月系中取值为0.01215；r1、r2表示航天器与地球和月球之间的距离，分别为

(2)

平动点、周期轨道和不变流形是限制性三体问题的主要特征。不变流形分为趋近于平动点周期轨道的稳定流形和远离周期轨道的不稳定流形，利用不变流形可进行主天体与平动点周期轨道之间的转移轨道设计。在计算过程中，通过施加微小扰动，使航天器偏离原周期轨道，得到流形积分初始点，对其进行积分则可得到相应不变流形，其初始点选取方法为

(3)

式中：x0为周期轨道上的点，Y为对应x0的单位特征向量，上角标s和u分别表示稳定流形不稳定流形，Xs(x0)和Xu(x0)分别为稳定流形和不稳定流形的积分初始点，ε表示小扰动量，在本文中取值为2×10-6。对流形积分初始点进行积分，即可得到相应不变流形。L1点halo轨道的稳定流形如图1所示。

图1 L1点halo轨道的稳定流形Fig.1 The stable invariant manifolds of L1 halo orbit

2 不变流形数值近似计算

由于不变流形不能到达地球附近区域，在对转移轨道进行设计时，航天器从近地停泊轨道出发后需要选择合适的位置进入流形，即对流形拼接点进行优化。传统的计算方法为通过积分得到流形点，由于在优化过程中，对选取不同拼接点时的性能进行分析对比，需要大量计算流形状态点，而基于数值积分的计算方法需要对整条流形进行积分才能得到某个状态点，计算量较大，计算效率较为低下。Topputo针对该问题提出了数值近似快速计算方法，通过二维插值，对流形状态点进行插值近似，在优化过程中不需要对流形重复积分，从而在满足计算精度的前提下，大大提高了计算效率[13]。

在积分得到流形状态点的过程中，只与参数τ和t有关，其中τ为对周期轨道初始点进行积分，并得到式中x0的积分时间，t为对稳定流形初始点Xs(x0)的积分时间，因此通过二维插值则可得到流形状态点。首先通过积分得到流形插值的原始数据，对积分流形的网格划分为

(4)

式中：T1为平动点周期轨道的周期，T2为流形的最大积分时间，对于稳定流形有T2<0，对不稳定流形则有T2>0，N和M为离散点数量。根据τi和tj则可积分得到相应的稳定流形点xs,ij(τ,t)。

得到插值的原始数据xs,ij后，对任意给定的(τ,t)进行计算的插值公式为

(5)

式中：ci+n,j+m为插值样点，h1=T1/(N-1)和h2=T2/(M-1)为离散步长，u为插值内核。

对于插值内核，设u(0)=1，u(n)=0，对其他值的计算式为

(6)

插值样点c为六维向量，分别对应流形状态点的三维位置矢量和三维速度矢量，计算公式为

(7)

(8)

(9)

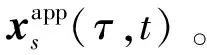
3 二体模型脉冲近似

在得到流形拼接点后，需要对近地停泊轨道和流形进行拼接。在限制性三体问题中，三体Lambert转移需要进行多次迭代计算，计算过程较为复杂。由于月球引力远小于地球引力，因此在计算拼接段时，可先利用地球-航天器二体模型进行近似计算，然后在三体模型下进行修正，从而降低计算难度和减小计算量。

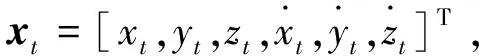
在二体模型下，根据经典轨道六要素，对于拼接段圆锥曲线，有

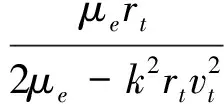
(10)

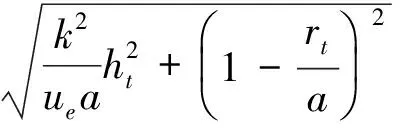
(11)

rp=a(1-e)

(12)

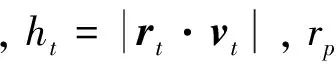
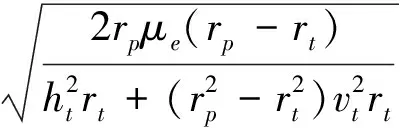
(13)

然后可计算得到航天器在拼接点所需施加的速度脉冲为

ΔvMI=(1-k)vt

(14)

到达近地停泊轨道后需要施加的速度脉冲为

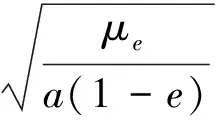
(15)

可得到二体模型近似下所需的速度增量为

Δvapp=ΔvE+ΔvMI

(16)

Φ(tp+Δt,xpr+Δxr)=Φ(tp,xpr)+

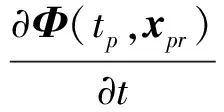
(17)

(18)

两个修正量对应两个约束方程，因此可求解得到Δt和p，从而计算得到三体模型下的拼接段以及完成拼接所需的速度增量ΔvEm和ΔvMIm。

4 主矢量理论

在1963年提出的主矢量理论中，Lawden给出的最优脉冲的必要条件为[15]：

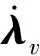
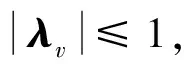
4)对于所有内点脉冲(初始时刻脉冲和终端时候脉冲除外)成立。

本文对限制性三体问题下的主矢量进行推导。在三体模型中，推力加速度近似为脉冲表示

(19)

(20)

式中：ti为施加脉冲时刻。

根据最优控制理论，构造哈密尔顿方程为

(21)

(22)

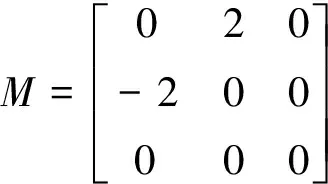
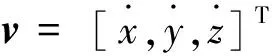
(24)

得到脉冲优化结果后，根据所施加的脉冲计算得到λv(t0)和λv(tf)，再以λr(t0)为迭代变量，根据边界条件λv(tf)求解出λr(t0)，然后积分得到主矢量λv在时间区间[t0,tf]上的值，判断是否满足所有Lawden必要条件，从而可判断优化得到双脉冲转移轨道是否为最优脉冲转移轨道。

5 数值仿真

考虑航天器从近地轨道出发，通过施加第一次脉冲进入拼接段，在流形拼接点处施加第二次脉冲进行L1点halo轨道的稳定流形，然后沿流形无动力的趋近于halo轨道。地球平均半径为6378.137km，近地停泊轨道为高度300km的圆轨道，L1点halo轨道的幅值Az为5000km。本算例中的计算在CPU为i7-4700MQ，主频为2.40GHz，内存为8G的计算机上进行，计算平台为MATLAB2015a。

考虑到实际任务中的飞行时间限制，流形积分时间上限为50天，同时为保证数值近似流形的精度，在halo轨道上均匀选取200个点，在每条流形上选取2001个点，作为流形插值数据库，即式中N=200，M=2001。为验证数值近似流形的精度，将其与积分得到的流形点进行误差对比分析。定义流形误差为

(25)

误差结果如表1所示，误差的对数lg(ξ)的分布情况如图2所示，可知平均精度为1.6529×10-6，相当于是0.6353km，在地月转移轨道设计过程中，该精度已属于较高精度，因此认为数值近似流形的精度足够满足转移轨道初步设计的要求。

表1 数值近似流形的误差情况Table 1 The error of the approximation invariant manifolds

选取τ=0时的流形，在该流形积分时间为[-50, -10]天的范围内，根据时间均匀选择160个点，对二体模型近似脉冲和三体模型修正后脉冲进行对比，如图3所示，其中ΔvEm和ΔvMIm为三体模型修正后所需的脉冲，对比分析可知，二体模型下的近似脉冲能很好地估计完成拼接段转移所需的速度增量。

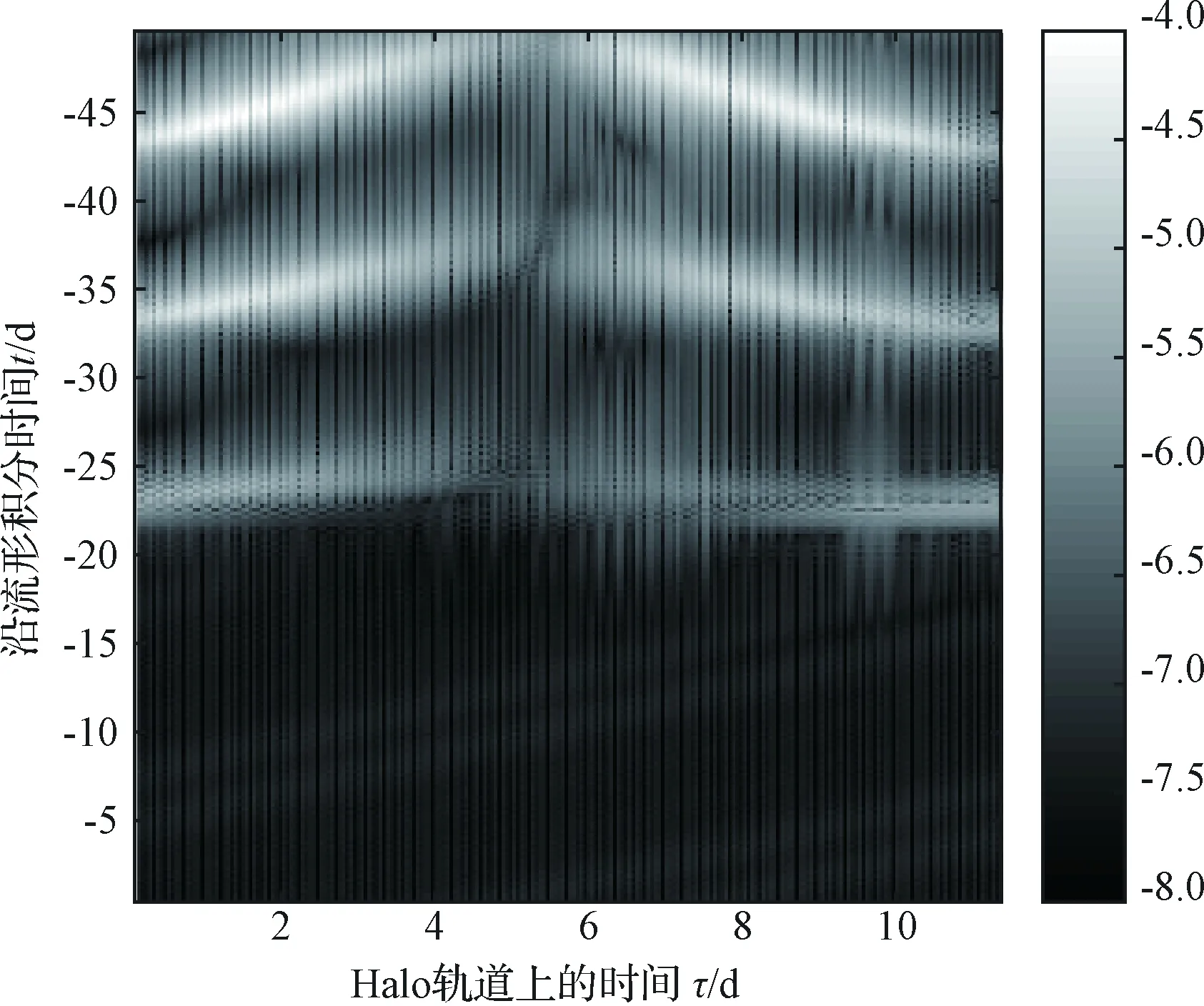
图2 数值近似流形的误差分析lg(ξ)Fig.2 The error pattern lg(ξ) of approximation invariant manifolds over the evaluation grid

对于拼接点的确定，利用MATLAB自带函数fmincon进行优化，优化变量为[τ,t]。在优化过程中，只利用二体模型脉冲近似，在得到优化结果后再在三体模型下进行修正，修正精度要求为1km。由于fmincon是局部优化函数，选取不同的初始值会得到不同的优化结果。多次选取不同的初始值，可得到4组优化结果，与图3中的单条流形的4个极小值点相对应。优化结果数据如表2所示，其中优化时间为只考虑fmincon函数优化的时间，4组结果所需优化时间均小于0.1s。这4组结果对应的转移轨道分别如图4～7所示，其中左图为旋转坐标系下的转移轨道，右图为地心惯性系下的转移轨道。从图4～7的(a)图可以看出，优化得到的4个拼接点均为流形的远地点，这是由于在远地点受到的地球引力较小，克服引力所消耗的能量较小，脉冲的利用率较大，因此完成转移所需的总速度增加较小；从右图可以看出，拼接点在流形上的位置相差约一个周期，结合表2中航天器沿流形的运动时间可知，流形绕地球运动一周所需时间约为10天。

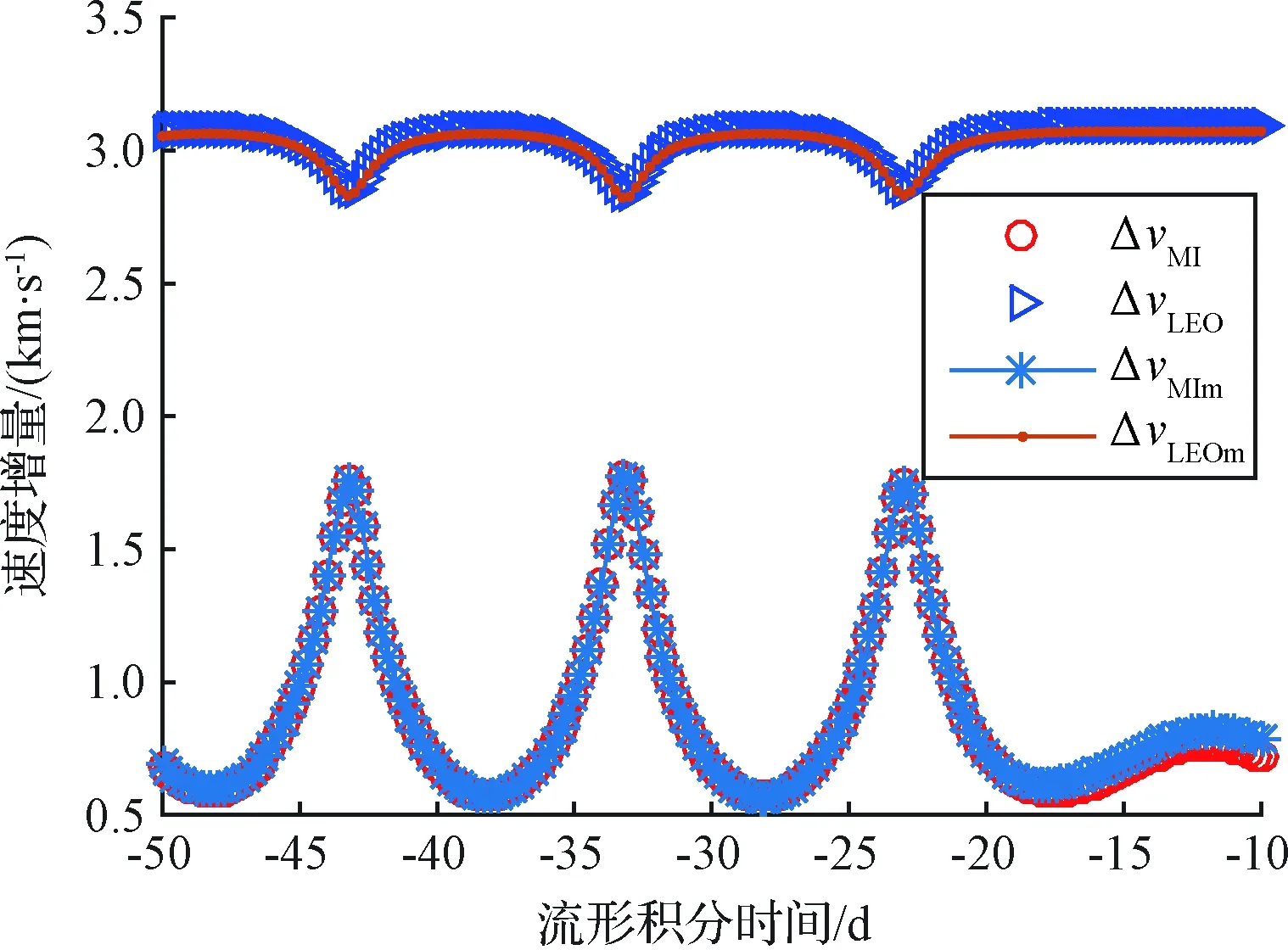
图3 二体模型近似脉冲与三体模型修正后脉冲对比Fig.3 Comparison of the two-body approximate impulse and the impulse modified in CRTBP

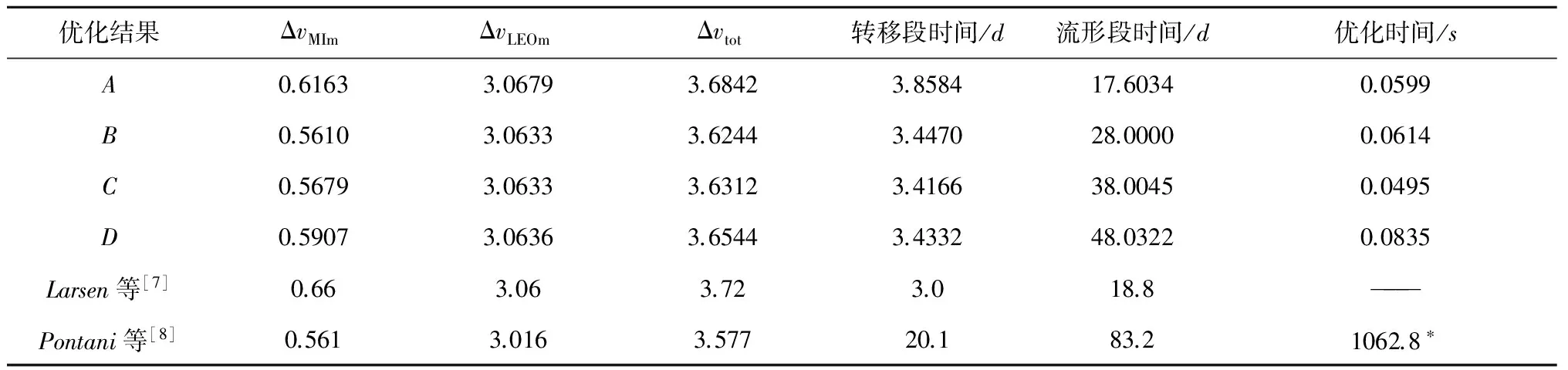
优化结果ΔvMImΔvLEOmΔvtot转移段时间/d流形段时间/d优化时间/sA0．61633．06793．68423．858417．60340．0599B0．56103．06333．62443．447028．00000．0614C0．56793．06333．63123．416638．00450．0495D0．59073．06363．65443．433248．03220．0835Larsen等[7]0．663．063．723．018．8———Pontani等[8]0．5613．0163．57720．183．21062．8∗

图4 双脉冲转移优化结果AFig.4 The results of two-impulse transfers: A

Larsen等[7]和Pontani等[8]均对航天器从地球到L1点周期轨道的双脉冲转移进行了研究，但仅考虑xy平面内的运动，目标轨道为L1点Lyapunov轨道。前者的近地停泊轨道高度为300km，后者的近地停泊轨道高度为500km，优化结果在表2中描述。文献[7]所需的速度增量小于本文优化结果主要是因为其近地停泊轨道的高度较高，克服地球引力所需能量较小；但对于相同高度的近地停泊轨道，本文的B组结果不论从转移时间还是所需速度增量，都要优于文献[8]中的结果。文献[11]对地月系下的双脉冲转移进行了详细研究，当目标halo轨道的横坐标为319052km时，对拼接点进行优化时，得到多个极小值点，该拼接点均为流形远地点，所需最小速度增量约为3.62km/s，与本文的优化结果类似。更为重要的是，利用文献[7]中的网格法进行优化时需耗费较长时间，文本作者复现文献[8]中的结果需用时1062.8s，利用[11]中计算单条转移轨道时也需要对施加脉冲进行打靶求解，而利用数值流形近似和二体模型脉冲近似方法，积分得到流形插值数据需耗时26.7s，然后利用fmincon函数求得上文中一个极小值解所需优化时间不到0.1s，因此本文的快速计算方法显著提高了计算效率。

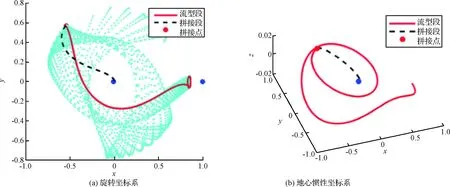
图5 双脉冲转移优化结果BFig.5 The results of two-impulse transfers: B

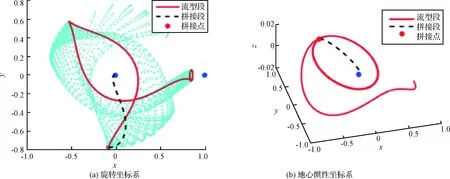
图6 双脉冲转移优化结果CFig.6 The results of two-impulse transfers: C

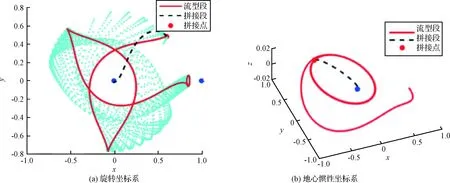
图7 双脉冲转移优化结果DFig.7 The results of two-impulse transfers: D

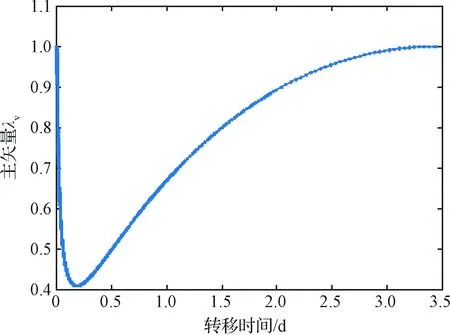
图8 B组优化结果的主矢量曲线Fig.8 The primer vector curve of result B

6 结 论

本文对限制性三体问题的平动点双脉冲转移轨道的快速计算方法进行研究。利用数值流形近似方法对流形进行插值并修正，从而避免了在优化过程中重复积分计算流形。对于确定的流形拼接点，以二体模型下的圆锥曲线作为拼接段的近似，根据经典轨道要素推导得到完成拼接所需的速度增量，再在三体模型下进行修正。最后利用推导得到的三体模型下的主矢量理论对优化结果是否满足燃料最优进行验证。通过数值仿真表明，结合这两种方法能在较短时间内得到优化结果，计算效率得到显著提升；并选取其中一条转移轨道，利用主矢量理论验证该脉冲转移轨道的燃料最优性，显示利用该方法在一定程度上能得到燃料最优转移轨道，从而表明该方法的合理性和高效性。

[1] Farquhar R, Kamel A. Quasi-periodic orbits about the translunar libration point [J]. Celestial Mechanics and Dynamical Astronomy, 1973, 7(4): 458-473.

[2] 徐明. 平动点轨道的动力学与控制研究综述[J]. 宇航学报, 2009, 30(4):1299-1313. [Xu Ming. Overview of orbital dynamics and control for libration point Orbits [J]. Journal of Astronautics, 2009, 30(4):1299 -1313.]

[3] 徐明, 徐世杰. 地-月系平动点及halo轨道的应用研究[J]. 宇航学报, 2006, 27(4):695-699. [Xu Ming, Xu Shi-jie. The application of libration points and halo orbits in the Earth-Moon system to space mission design [J]. Journal of Astronautics, 2006, 27(4):695 -699.]

[4] 侯锡云, 刘林. 共线平动点的动力学特征及其在深空探测中的应用[J]. 宇航学报, 2008, 29(3):736-747. [Hou Xi-yun, Liu Lin. The dynamics and applications of the collinear libration points in deep space exploration [J]. Journal of Astronautics, 2008, 29(3):736 -747.]

[5] Cosgrove D, Frey S, Bester M, et al. Navigating THEMIS to the ARTEMIS low-energy lunar transfer trajectory[C]. SpaceOps 2010 Conference, Alabama, USA. April 25-30, 2010.

[6] 连一君. 基于三体平动点的低能转移轨道设计研究[D]. 长沙：国防科学技术大学, 2008. [Lian Yi-jun. Research on low-cost transfer trajectories design based on three-body libration points [D]. Changsha: National University of Defense Technology, 2008. ]

[7] Larsen A, Anthony W, Critz T, et al. Optimal transfers with guidance to the Earth-Moon L1and L3libration points using invariant manifolds: a preliminary study [C]. AIAA/AAS Astrodynamics Specialist Conference, Minnesota, USA. August 13-16, 2012.

[8] Pontani M, Teofilatto P. Low-energy Earth-Moon transfers involving manifolds through isomorphic mapping [J]. Acta Astronautica, 2013, 91(10):96-106.

[9] 张汉清, 李言俊. 地月三体问题下L1-地球低能转移轨道设计[J]. 哈尔滨工业大学学报, 2011, 43(5):84-88. [Zhang Han-qing, Li Yan-jun. Design of L1-Earth low energy transfer trajectory in Earth-Moon three-body problem [J]. Journal of Harbin Institute of Technology, 2011, 43(5):84-88.]

[10] Davis K, Born G, Butcher E. Transfers to Earth-Moon L3 halo orbits [J]. Acta Astronautica, 2013, 88(3):116 -128.

[11] Parker J S, Born G H. Direct lunar halo orbit transfers [J]. The Journal of the Astronautical Sciences, 2008, 56(4):441-476.

[12] Parker J S, Anderson R L, Peterson A. Surveying ballistic transfers to low lunar orbit [J]. Journal of Guidance Control & Dynamics, 2013, 36(5):1501 -1511.

[13] Topputo F. Fast numerical approximation of invariant manifolds in the circular restricted three-body problem [J]. Communications in Nonlinear Science & Numerical Simulation, 2016, 32:89-98.

[14] 张仁勇. 深空探测小推力低能转移轨道设计方法研究[D]. 西安：西北工业大学, 2015. [Zhang Ren-yong. Research on low-thrust low-energy transfer trajectory design for deep space exploration [D]. Xi’an: Northwestern Polytechnical University, 2015. ]

[15] Lawden D F. Optimal trajectories for space navigation [J]. Mathematical Gazette, 1964, 48(366):478.

[16] Shen H, Casalino L. Indirect optimization of three-dimensional multiple-impulse Moon-to-Earth transfers [J]. The Journal of the Astronautical Sciences, 2014, 61(3):1-20.

通信地址：陕西省西安市碑林区友谊西路127号西北工业大学251信箱(710072)

电话：15191433469

E-mail：xpan2012@gmail.com

An Efficient Calculation Method for Two-Impulse Transfers to Libration Point

PAN Xun1,2, YANG Rui1,2, PAN Bin-feng1,2,TANG Shuo1

(1. School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China;2. National Key Laboratory of Aerospace Flight Dynamics, Xi’an 710072, China)

An efficient calculation method is proposed for the optimization of the two-impulse transfers to the librations in circular restricted three-body problem. With the invariant manifolds approximation based on a two-dimensional interpolation, the computation of the great number of manifold insertions is much more efficient. While the conic curve in a two-body problem used as an approximation of the transfer segment connecting the low Earth orbit and the stable manifold, the maneuvers can be deduced with the classical orbital elements, thus the iterative computation of the maneuvers is avoided in the optimization process. Then the primer vector of CRTBP is deduced to verify the optimality of the two-impulse transfer. At last, a numerical simulation of the two-impulse transfer from a low Earth orbit to aL1point halo orbit is presented, verifying the validity of the two-body impulse approximation and the manifold approximation, and demonstrating the efficiency of the method.

Circular restricted three-body problem; Libration point; Invariant manifolds approximation; Primer vector theory; Trajectory optimization; Earth-Moon transfers

2017-01-09;

2017-04-21

国家自然科学基金(11672234)

V448.2

A

1000-1328(2017)06-0574-09

10.3873/j.issn.1000-1328.2017.06.003

潘 迅(1990-)，男，博士生，主要研究方向为飞行动力学与控制，深空探测轨道优化设计。