考虑执行器安装偏差的航天器姿态跟踪控制

李冬柏，解延浩，吴宝林

(哈尔滨工业大学卫星技术研究所，哈尔滨150080)



考虑执行器安装偏差的航天器姿态跟踪控制

李冬柏，解延浩，吴宝林

(哈尔滨工业大学卫星技术研究所，哈尔滨150080)

针对存在执行器安装偏差和外干扰力矩的航天器姿态跟踪问题，提出了一种基于滑模控制的鲁棒控制律。控制律考虑了因执行器安装偏差导致的控制力矩偏差，且抑制了其对姿态控制精度的影响。在控制律设计时，除了保证系统稳定性外，还进一步给出了明确的与控制参数相关的姿态跟踪误差上界。数学仿真结果表明了此控制方案的有效性。

飞行器；姿态跟踪；执行器安装偏差；鲁棒控制

0 引 言

在航天器姿态控制系统中，由于制造公差或结构变形，不可避免的会存在执行机构安装偏差。在姿态稳定问题中，较小的执行器安装偏差对控制性能的影响并不显著。然而，对于姿态跟踪，特别是快速跟踪问题，执行器安装偏差将会引起明显的姿态角和姿态角速度跟踪误差。而事实上在某些特殊情况下，例如快速响应航天器研发中，由于时间的关系，执行器安装甚至可能没有经过充分校准便投入使用。因此，在高精度姿态跟踪控制系统的设计与分析中，必须考虑执行器的安装误差问题。

在现有文献中，在航天器的姿态控制方法的研究方面已取得了丰富的成果，如自适应控制[1-4]，最优控制[5-6]，滑模控制[6-10]，和迭代学习控制[11]等等，但涉及执行器偏差问题的研究并不多。文献[12]提出，可用自适应控制法来解决可变速控制力矩陀螺的安装偏差问题。但是，此方法中要估计的参数的个数为12n+3个，其中n为飞轮的数量。较多的自适应参数将使控制律的实现过于复杂。此外，由于持续激励不足，估计参数难以收敛至实际值。而在文献[13]中，针对存在执行器偏差的姿态稳定问题，作者提出了另一种自适应控制律。但文中只推导出了考虑执行器安装偏差下的输入状态稳定性。在存在执行器安装偏差时，并不能保证最终有界稳定。

本文研究了考虑执行器安装偏差的航天器姿态跟踪控制问题。执行机构安装偏差会导致姿态动力学模型不确定，而这一模型不确定性又与控制力矩相关，这将给姿态控制系统设计带来很大困难。因此本文提出了一种鲁棒控制律来解决此问题。可以证明，通过选择合适的设计参数，能保证系统最终有界稳定。它也确保了最终的姿态跟踪误差与设计参数成比例，从而可调。最后，仿真结果验证了所提出的控制方案的有效性。

1 航天器姿态动力学模型

刚性航天器姿态跟踪误差动力学模型如下：

(1)

(2)

(3)

式中：ωd∈3表示航天器本体坐标系相对于惯性坐标系的目标角速度；ω∈3表示航天器本体坐标系相对于惯性系的角速度；δω=ω-R(δq)ωd表示角速度误差；R(δq)为从航天器参考坐标系到本体系的姿态旋转矩阵；表示误差四元数；δqv∈3和δq0∈表示误差四元数的矢量和标量部分；z∈3表示干扰力矩；I3表示三阶单位矩阵；J∈3×3表示转动惯量矩阵。记号a×表示向量构成的一个反对称矩阵：

u=[u1,u2,…,un]T∈n,n≥3

式中：ui,i=1,2,…,n表示第i个执行器提供的控制力矩；D=[d1,d2,…,dn]∈3×n为执行器的分配矩阵，其中di∈3,i=1,2,…,n表示在本体坐标系下，第i个执行器的方向单位向量。di可以写成di=dn,i+Δdi，在这里dn,i和Δdi表示方向单位矢量的标称部分和不确定部分。不确定部分Δdi即来自于执行器的安装误差。因此，分配矩阵D可以表示为

D=Dn+ΔD

(4)

式中：Dn和ΔD分别表示执行器分配矩阵的标称部分和不确定部分。其中，标称值：Dn=[dn,1,dn,2,…,dn,n]，由安装偏差导致的不确定部分：ΔD=[Δd1,Δd2,…,Δdn]。

关于外部扰动的假设如下：

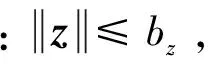
2 问题描述

使用如下的伪逆法分配控制力矩：

(5)

式中：τ∈3表示本体坐标系下的控制力矩。

将式(5)代入式(1)得到

(6)

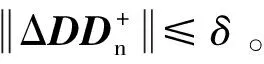
本文的控制目标是设计一个鲁棒控制律τ，并在存在执行机构安装偏差和外干扰力矩的前提下，确保姿态角和姿态角速度跟踪误差收敛到一个包含原点的小区间内。从式(2)、式(3)和式(5)可以看出，航天器姿态跟踪问题可以等价的视作一个对于δω和δq的渐近稳定问题。一个存在执行器安装偏差的姿态跟踪控制系统示意图如图1所示：

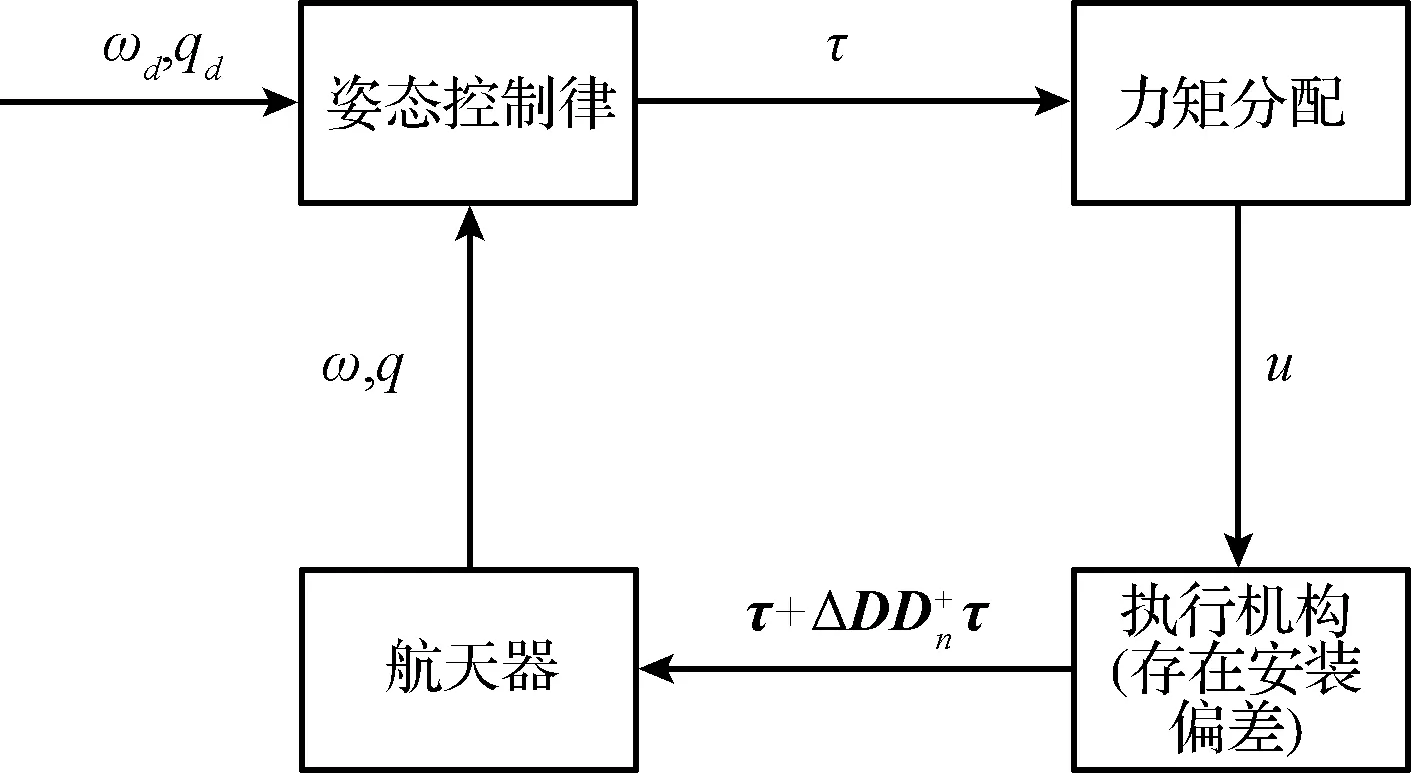
图1 考虑执行器安装偏差的姿态跟踪系统结构图Fig.1 Structure of the attitude tracking control system with actuator misalignments

3 鲁棒控制律

本节针对式(2)、式(3)和式(6)描述的姿态跟踪控制系统，提出了一个鲁棒反馈控制律。为设计控制方法，定义如下滑模矢量：

s=δω+βδqv

(7)

式中：δqv表示误差四元数的矢量部分，用来描述航天器姿态跟踪误差；而δω表示角速度跟踪误差，β是一个正的常数。

文献[14]证明，在滑动面s=0上，随着t→∞，姿态角误差和角速度误差趋于零，即：

(8)

由式(2)、式(3)和式(7)可得：

(9)

定义：

L(·)= -ω×Jω+J(δω×R(δq)ωd(t)-

(10)

鲁棒控制律设计如下：

τ=-L(·)-kssφ-kSAT(s,φ)

(11)

式中：L(·)由式(10)定义；ks和k为由设计者设定的正常数。式(11)中，SAT(s,φ)的定义为：

SAT(s,φ)

(12)

式中：s1,s2,s3是向量s的元素,饱和函数定义如下：

(13)

式(11)中的sφ定义如下：

sφ=[sφ,1,sφ,2,sφ,3]T

(14)

式中：

sφ,i=si-φsat(si,φ),i=1,2,3

(15)

式中：sφ,i用于衡量当前状态量到边界层的代数距离[15]。

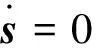
注3．根据文献[16]方法，式(11)中的反馈增益ks和式(7)中滑模矢量的参数β取值由下式确定：

(16)

(17)

式中：ts表示由系统任务确定的响应时间，仿真中取ts=60s。

对于姿态跟踪闭环系统可以得到以下定理：

定理1. 对于存在执行器安装偏差的姿态跟踪系统(1)～(3)，采用控制律(5)和(11)。如果假设1和2成立，且控制增益k满足：

(18)

则式(14)中定义的变量sφ将逐渐收敛到零。

证明：选取李雅普诺夫函数

(19)

(20)

把式(11)中的控制律代入式(20)可得：

(21)

由sat(s,φ)和sφ的定义，得到：

(22)

因此，由式(22)可得：

(23)

结合式(21)和式(23)可得：

(24)

考虑到假设1和2，式(24)可写为：

(25)

将控制输入(11)代入式(25)中：

(26)

式(26)可整理得到：

(27)

如果条件(18)成立，则上述方程可简化为：

(28)

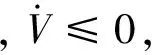
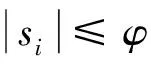
由定理1和注5可见，滑模矢量s将收敛到一个包含原点的小区间内。因此，δω和δqv都将收敛到一个小区间内，这一点可由以下定理得出：

(29)

上面的方程可以改写为如下形式

(30)

由式(30)，当

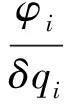
(31)

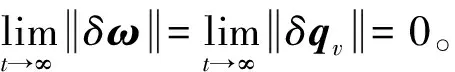
因此，由式(30)和式(31)可知，姿态误差将收敛到区间：

(32)

由式(29)，有：

(33)

注意到：

(34)

结合式(32)～(34)，得到角速度误差的范围：

(35)

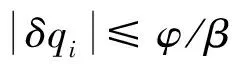
4 仿真校验

本节以仿真算例验证所提出控制方案的有效性。航天器的转动惯量矩阵假设如下：

为了体现执行机构安装偏差对姿态控制性能的影响，在仿真中假定外部干扰为零。三个执行器被安装在航天器本体坐标系的三个主轴上。理想分配矩阵，不确定部分和实际分配矩阵假设如下：

实际分配矩阵由理想矩阵沿坐标轴轻微偏转1°获得。仿真中考虑了控制力矩饱和0.5N·m。

仿真中考虑两种情况：在情形A中，使用文献[16]中的类PD姿态控制器如下：

(36)

在情形B下，使用式(5)和式(11)中的控制器。控制器参数ks和β由式(16)和式(17)确定。φ设定为φ=0.0001。k设定为k=0.015以满足条件。

情形A：本情形下使用式(5)和式(36)中的类PD姿态跟踪控制器，仿真计算结果如图2～4所示。为了使结果直观，将姿态误差从姿态四元数转换成欧拉角输出。从图2可知，由于执行器安装误差，姿态的稳态跟踪误差达0.08°。可见，执行机构的安装误差对姿态控制精度有明显的影响，因此在设计和分析高精度的姿态控制系统时应考虑到执行机构安装误差的影响。

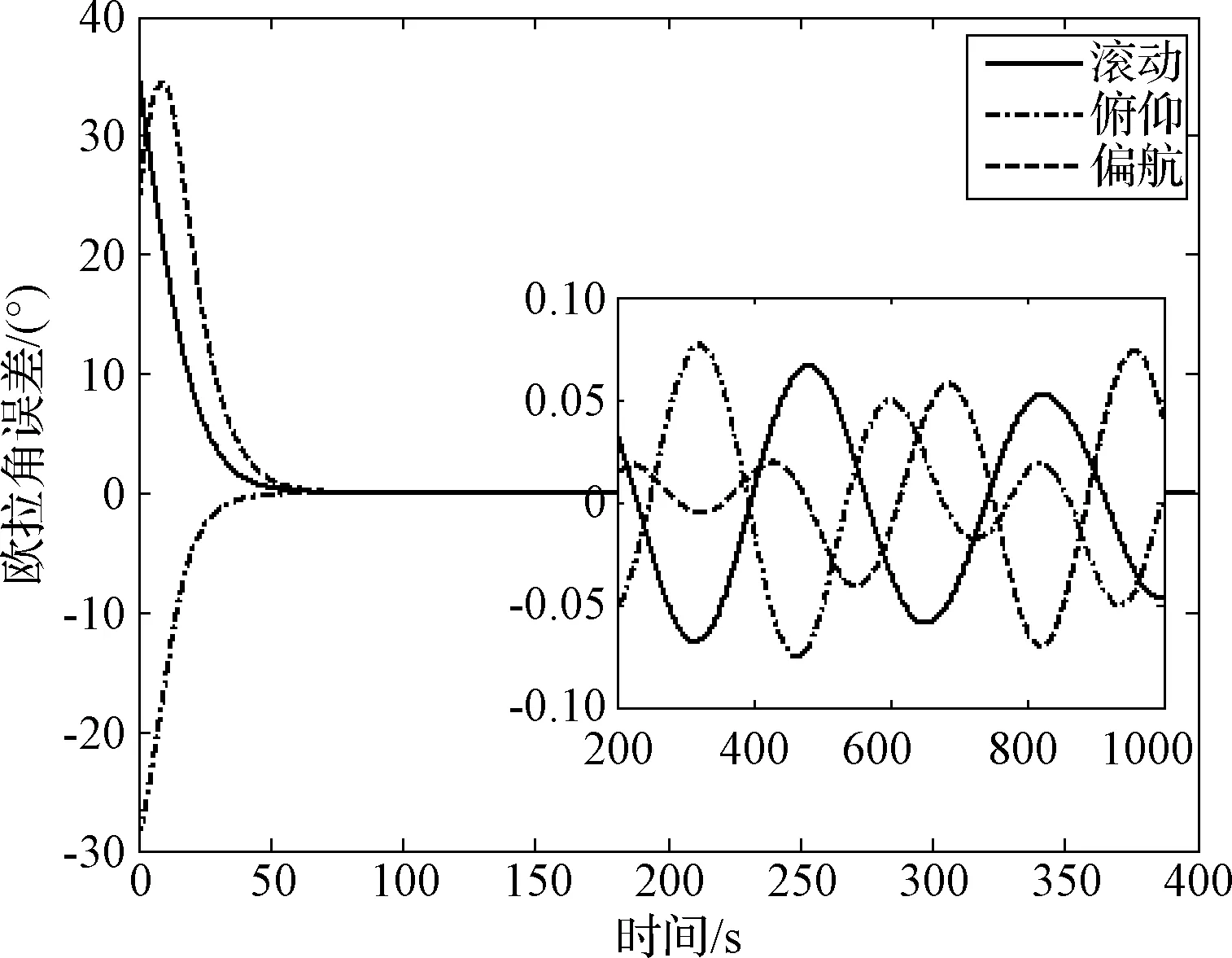
图2 情形A下的姿态跟踪误差Fig.2 Attitude tracking errors in case A

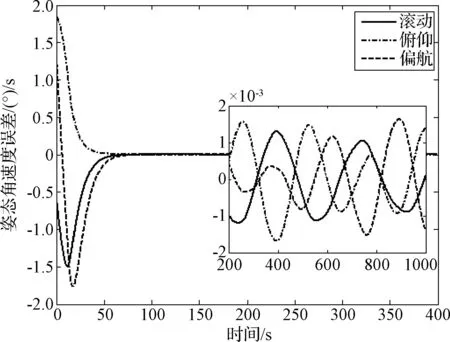
图3 情形A下的角速度跟踪误差Fig.3 Angular velocity tracking errors in case A

图4 情形A下的控制力矩Fig.4 Control torqueτin case A

情形B：在这种情况下，系统使用式(5)和式(11)中提出的姿态跟踪控制器。姿态角跟踪误差、姿态角速度跟踪误差和控制力矩如图5～7所示。由图5可以看出，相比情形A，稳态误差大大减少至0.008°。从图4和图7可见，在稳态过程中，两种情况下的控制力矩是相似的。因为两个控制器几乎是相同的，除了情形B中控制器相比前者多了一个附加项kSAT(s,φ)。可见虽然附加项kSAT(s,φ)的值较小，但显然它对于抑制执行器安装误差的影响是有效的。仿真结果验证了本文理论，并证明了所提出的控制方案的有效性。

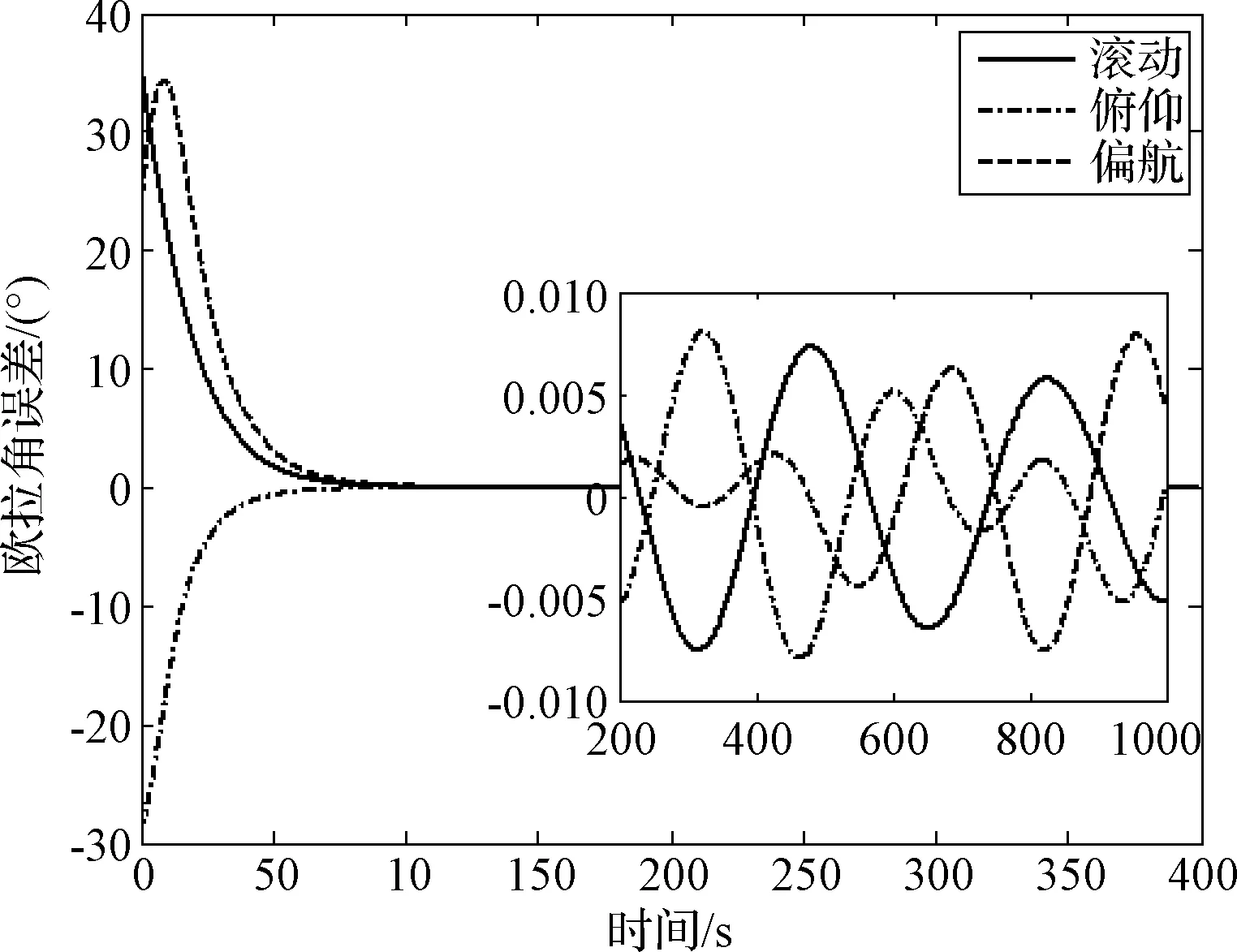
图5 情形B下的姿态跟踪误差Fig.5 Attitude tracking errors in case B

图6 情形B下的角速度跟踪误差Fig.6 Angular velocity tracking errors in case B

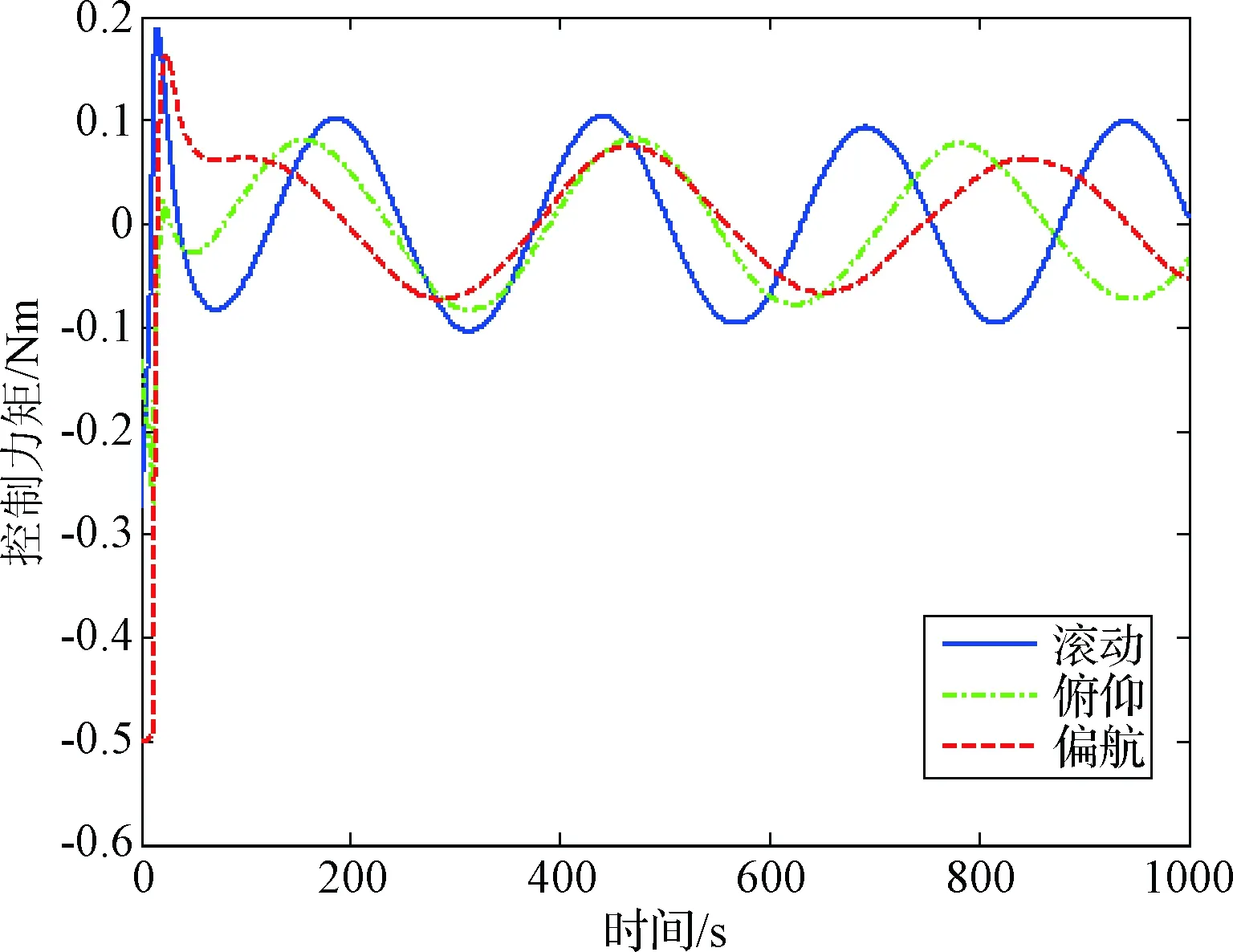
图7 情形B下的控制力矩Fig.7 Control torque τ in case B

5 结 论

研究了考虑执行器安装误差和外部干扰的航天器姿态跟踪问题，并针对问题提出了一种鲁棒控制律。在设计过程中，除了保证系统稳定性外，还给出了明确的跟控制参数相关的姿态跟踪误差上界。仿真结果表明，与具有相同控制增益的常规控制器相比，所提出的控制器能大大减少姿态跟踪误差。因此，可以得出结论，该控制器能有效地克服执行器安装偏差和外部干扰对姿态控制的影响。

[1] Ahmed J, Coppola V T, Bernstein D S. Adaptive asymptotic tracking of spacecraft attitude motion with inertia matrix identification[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(5): 684-691.

[2] Cai W C, Liao X H, Song Y D. Indirect robust adaptive fault-tolerant control for attitude tracking of spacecraft[J].Journal of Guidance, Control, and Dynamics, 2008, 31(5): 1456-1463.

[3] 解永春,牟小刚,吴宏鑫,等. 挠性航天器大角度机动的全系数自适应控制[J]. 宇航学报,1999,20(2):1-6. [Xie Yong-chun, Mou Xiao-gang, Wu Hong-xin，et al. The all-coefficient adaptive control of the slew maneuver of a flexible spacecraft[J]. Journal of Astronautics, 1999, 20(2) :1-6.]

[4] 李冬柏，吴宝林，张迎春. 考虑未知飞轮摩擦力矩的航天器姿态跟踪鲁棒自适应控制[J]. 宇航学报, 2016, 37(2):175-181. [Li Dong-bai, Wu Bao-lin, Zhang Ying-chun. Robust adaptive control for spacecraft attitude tracking with unknown friction torque of reaction wheel [J]. Journal of Astronautics, 2016, 37(2) : 175-181.]

[5] Luo W, Chu Y C, Ling K V. Inverse optimal adaptive control for attitude tracking of spacecraft[J]. IEEE Transactions on Automatic Control, 2005, 50(11): 1639-1654.

[6] 宋道喆, 耿云海, 易涛. 零角动量欠驱动航天器逆最优稳定控制律设计[J]. 宇航学报, 2016, 37(6):729-736. [Song Dao-zhe, Geng Yun-hai, Yi Tao. Inverse optimal stabilization of an underactuated spacecraft in a zero angular momentum mode[J]. Journal of Astronautics, 2016, 37(6): 729-736.]

[7] Boskovic J D, Li S M, Mehra R K. Robust adaptive variable structure control of spacecraft under control input saturation[J]. Journal of Guidance, Control, and Dynamics, 2001, 24(1): 14-22.

[8] 李波,胡庆雷,石忠,等. 考虑执行器安装偏差时航天器姿态稳定的控制分配[J]. 宇航学报, 2013, 34(1):25-31. [Li Bo, Hu Qing-lei, Shi Zhong, et al. Dynamic control allocation for attitude stabilization of spacecraft considering actuator misalignment [J]. Journal of Astronautics, 2013, 34(1): 25-31.]

[9] Wu B L, Wang D W, Poh E K. Decentralized robust adaptive control for attitude synchronization under directed communication topology[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(4): 1276-1282.

[10] Guo Y, Song S, Li X. Quaternion-based finite-time control for attitude tracking of the spacecraft without unwinding[J]. International Journal of Control Automation and Systems, 2015,13(6):1351-1359.

[11] Wu B L, Wang D W, Poh E K. High precision satellite attitude tracking control via iterative learning control[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(3): 528-534.

[12] Yoon H, Tsiotras P. Adaptive spacecraft attitude tracking control with actuator uncertainties[J]. Journal of the Astronautical Sciences, 2008, 56(2): 251-268.

[13] Hu Q L, Xiao B, Wang D W, Poh E K. Attitude control of spacecraft with actuator uncertainty[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(6): 1771-1776.

[14] Vadali S. Variable structure control of spacecraft large angle maneuvers[J]. Journal of Guidance, Control, and Dynamics, 1986, 9(2): 235-239.

[15] Slotine J J E, Coetsee J A. Adaptive sliding controller synthesis for non-linear systems[J]. International Journal of Control, 1986,43: 1631-1651.

[16] Wie B, Weiss H, Arapostathis A. Quaternion feedback regulator for spacecraft eigenaxis rotations[J]. Journal of Guidance, Control and Dynamics,1989, 12 (3): 375-380.

通信地址：哈尔滨市南岗区一匡街2号科学园B3栋3012信箱(150080)

电话：(0451) 86402357转8512

E-mail: watermonth@163.com

吴宝林(1983-)，男，副教授，主要从事卫星姿态控制，姿态协同控制研究。本文通信作者。

通信地址：哈尔滨市南岗区一匡街2号科学园B3栋3012信箱(150080)

电话：(0451) 86402357转8507

E-mail：wubaolin@hit.edu.cn

Robust Spacecraft Attitude Tracking Control with Actuator Misalignments

LI Dong-bai, XIE Yan-hao, WU Bao-lin

(Research Center of Satellite Technology, Harbin Institute of Technology, Harbin 150080, China)

A sliding mode control-based robust control law is proposed to deal with the problem of spacecraft attitude tracking considering actuator misalignments and external disturbances.The control torque errors due to actuator misalignments are considered in the proposed control law, and its effects on attitude control performance are suppressed. Besides showing stability, explicit bound on the attitude tracking errors is given in terms of design parameters. Simulation results show the effectiveness of the proposed control scheme.

Spacecraft; Attitude tracking; Actuator misalignment; Robust control

2016-05-26;

2017-01-18

国家自然科学基金(61503093,91438202)；哈尔滨工业大学资助项目(AUGA5710053114)；微小型航天器技术国防重点学科实验室开放基金(HIT.KLOF.MST.201502)

V448.2

A

1000-1328(2017)06-0598-07

10.3873/j.issn.1000-1328.2017.06.006

李冬柏(1980-)，男，副研究员，主要从事卫星姿态控制，轨道控制研究。