我国新型金融状况指数的构建与物价预测

陈 磊，咸金坤，隋占林

(1.东北财经大学 经济学院，辽宁 大连 116025；2.东北财经大学 经济计量分析与预测研究中心，辽宁 大连 116025)

·金融与投资·

我国新型金融状况指数的构建与物价预测

陈 磊1,2，咸金坤1，隋占林1

(1.东北财经大学 经济学院，辽宁 大连 116025；2.东北财经大学 经济计量分析与预测研究中心，辽宁 大连 116025)

本文利用时变因子载荷矩阵TVP-FAVAR模型提取出相关金融变量的共同因子，并借助动态模型选择方法筛选每期的最优因子，以此构建了我国新型金融状况指数(FCI)，从相关性、因果关系和预测能力等视角分析了FCI与通胀率之间的关系。结果显示：以时变参数和时变维度方法构建的新型FCI与我国宏观经济现实吻合程度较好；相对于传统方法，本文构建的FCI与通胀率之间具有较高的相关性和较低的预测误差，且FCI相对通胀率平均先行2—3个月，能够较好地预测通胀的短期未来走势，可以作为货币政策制定的参考指标。

金融状况指数(FCI)；通胀率；物价预测；TVP-FAVAR模型

一、引 言

随着我国金融体系的不断发展与完善，金融市场在宏观经济运行中的作用日益凸显。2008年全球金融危机对各国实体经济产生的严重影响使人们再次认识到改进和完善金融体系监测和预警管理的重要性与紧迫性，如何准确地度量宏观金融状况已经成为后金融危机时期经济学界普遍关注的问题之一。2012年以来，在外部环境不确定性加大的同时，我国经济发展进入了增速放缓、结构调整和动力转换的“新常态”阶段，经济环境变得更为复杂。针对近年来我国经济运行出现的新形势，本文旨在运用先进的计量分析手段构建能够灵活、准确反映金融市场整体运行情况的金融状况指数，进而应用该指数提高对我国通货膨胀监测与预警的效果。

21世纪以来，作为综合各类重要金融变量信息的综合性指标，金融状况指数(Financial Condition Index，FCI)成为反映金融市场整体运行情况的典型代表。由Goodhart和Hofmann[1]提出的FCI最早可追溯到加拿大银行的货币状况指数(MCI)，MCI是短期利率与汇率的加权平均，用以反映一国货币政策立场。不同于MCI，FCI还考虑了资产价格等信息，因而可以更全面地反映货币政策导向和未来通货膨胀压力，从而更好地预测未来宏观经济走势。

总结相关文献(如栾惠德和侯晓霞[2])可以发现，目前构建FCI的方法主要有三大类：加权求和方法、主成分分析方法以及动态因子分析方法。在加权求和方法中，通过为各个金融变量赋予合适的权重以得到FCI。而权重的分配主要基于各金融变量的变化对通胀或GDP影响的大小，通常通过大型宏观经济模型模拟、VAR模型的脉冲响应函数或总需求方程简化式等方法测算变量权重。在主成分分析方法中，一般根据一定的判断准则选取前几个主成分，并以它们各自的贡献率为权重合成FCI。而动态因子分析方法通常是事先根据经济理论和先验判断确定金融变量，并从中提取出他们的共同因子，以此作为FCI。

国外学者对这三类方法的应用展开了较为深入的研究。Goodhart和Hofmann[3]利用总需求方程简化式以及VAR模型构建了G7国家的FCI，研究结果表明FCI对通货膨胀具有较强的预测能力。Gauthier等[4]基于IS曲线、广义脉冲响应函数以及因子分析法构建了加拿大的FCI，结果显示FCI能够较为准确地描绘出经济周期转折点，对产出也具有较好的预测能力。Angelopoulou等[5]利用主成分分析法构建了欧元区国家的FCI，分析了其对货币政策的指示作用。Hatzius等[6]利用近似动态因子模型构建了美国的FCI，并提出了FCI中应该剔除宏观经济成分，从而准确度量金融冲击的思想。Matheson[7]采用动态因子模型构建了美国和欧洲地区的FCI，并考察了其对实际经济活动预测的有效性。然而，上述研究都基于常系数模型构建FCI，而Koop和Korobilis[8]从计量经济方法上对FCI的构建做出了较大改进，他们运用具有时变参数和时变维度的因子增广向量自回归(Factor-Augment-Vector-AutoRegression Model With Time-Varying Parameters，TVP-FAVAR)模型构建了美国的季度FCI，实证研究结果显示，该指标对产出和失业率具有很好的预测效果，并且与现有FCI或金融压力指数(FSI)相比，该指数在反映宏观经济现实运行情况上也具有明显的优势。

近年来，国内一些学者开始致力于我国FCI的构建，并将其应用于通货膨胀或产出的预测，进而探讨其作为货币政策参考指标与指示器的可行性。从现有的文献看，国内的研究主要是通过VAR模型的脉冲响应函数确定金融变量的权重，然后加权求和以构建FCI，如戴国强和张建华[9]、陆军等[10]、封思贤等[11]、徐涤龙和欧阳胜银[12]、周德才等[13]。但是陆军和梁静瑜[14]认为VAR模型方法在变量的选择以及模型的识别上存在争议性。另外，也有一些国内学者利用总需求方程简化式构建FCI，如陆军和梁静瑜[14]、余辉和余剑[15]、肖强和司颖华[16]，然而该方法的可靠性依赖于模型中各变量相互外生，但这一假设通常很难在现实中成立。王维国等[17]率先在我国探索使用小型联立方程模型构建FCI，并取得了良好的效果。还有一些学者使用主成分分析或因子分析方法构建FCI，与加权求和方法相比，通过这两种方法构建的FCI避免了模型依赖性问题，并且能够容纳更多的经济指标，但目前这类研究在国内尚不多见。其中，邓创和徐曼[18]采用主成分分析方法提取了我国的FCI，并借助TVP-VAR模型分析了金融冲击对宏观经济影响的时变特性。栾惠德和侯晓霞[2]采用混频动态因子模型(ADS方法)构建了实时FCI，极大地提高了FCI监测与预警效果的时效性。

尽管国内关于FCI的研究取得很大进展，但仍存在一些不足之处。FCI通常由较长跨度的时间序列数据估计得到，传统方法未能体现出样本期内经济结构的变化情况。陆军和梁静瑜[14]、周德才等[13]曾指出，以常系数模型构建FCI不适合金融和经济结构正在转型中的我国，因而若考虑到模型参数的不稳定性，采用时变参数模型构建FCI则更加符合现实。现有成果均假设在样本期内用于构建FCI的指标个数不变，而如果在不同的经济发展阶段灵活选择构建FCI的金融指标，则有助于降低模型过度参数化的风险，或避免因参数收缩度*通常在包含大量解释变量的模型中需要施加大量的假设性限制，而参数收缩度就是用来控制这种假设性限制强弱的指标。设置不当而造成模型错误设定，从而可能会提高FCI构建和预测的准确性。Boivin和Ng[19]认为，在因子分析中，用以提取共同因子的变量个数一成不变并不一定是最优选择。Koop和Korobilis[20]、郭永济等[21]的研究表明，时变维度的模型在经济预测中往往效果更好，而Koop和Korobilis[8]在构建美国的季度FCI时的研究结果也说明时变维度模型更符合现实。

基于以上分析，本文借鉴Koop和Korobilis[8]的方法试图从以下三个方面对我国FCI的构建有所突破：第一，利用具有时变因子载荷矩阵的TVP-FAVAR模型构建FCI。该模型允许因子载荷矩阵随时间而变化，而因子载荷可以认为是各金融变量在FCI中所占的比重，因此，时变的因子载荷矩阵可以反映出各金融变量在FCI中构成权重的变化，进而可以刻画出我国金融市场与经济结构可能发生的变化。第二，根据Hatzius等[6]的建议，在构建FCI时引入宏观经济变量作为控制变量以剔除FCI中的宏观成分，从而提高FCI构建的准确性。第三，为了避免变量选择的主观性而导致构建的FCI遗漏重要信息或引入无关干扰信号，本文利用动态模型选择(Dynamic Model Selection，DMS)技术灵活选择进入模型的金融变量，使构建FCI的变量具有时变特征。

二、TVP-FAVAR模型及其估计

(一)具有时变因子载荷矩阵的TVP-FAVAR模型构建

时变因子载荷矩阵TVP-FAVAR模型可以表示成如下形式：

(1)

(2)

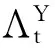
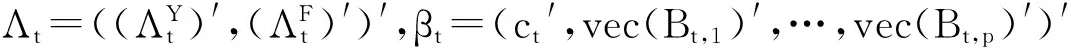
Λt=Λt-1+vt

(3)

βt=βt-1+ηt

(4)

其中，vt～N(0,Wt)，ηt～N(0,Rt)，并且假定方程中的误差项不相关。

由式(1)—式(4)构成的模型即为具有时变因子载荷矩阵的TVP-FAVAR模型。在利用该模型构建FCI时，由于模型的因子载荷矩阵是随时间变化的，而因子载荷可以认为是金融变量在FCI中所占的比重，因此，时变的因子载荷矩阵可以反映出各金融变量构成权重的变化。

(二)时变维度的TVP-FAVAR模型构建

在金融变量Xt所有的子集中，不同的变量组合所构建的FCI也是不同的。如集合Xt中有n个金融变量，其中m个变量始终包含在模型中，即下文中的固定变量，那么将会有2(n-m)个非空子集，这些子集中分别包含不同的金融变量，从而会有2(n-m)个不同的TVP-FAVAR模型提取出各自的FCI。为了避免变量选择的主观性，同时考虑到目前我国金融市场与经济结构正在进行不断的转型与调整，本文不事先设定用以构建FCI的变量总数目，而是由模型和数据特征决定每一期进入模型用于提取FCI的变量，以及模型中包含的变量总个数。由此，随着金融市场和经济结构的变化，用于提取FCI的变量也是变化的，即时变的模型维度。具体来看，根据进入模型的变量不同，共有j=1,…,J个模型，第j个模型Mj可以表示成如下形式：

(5)

(6)

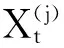
根据上文介绍可知，在t时刻共有2(n-m)个不同模型构建不同的FCI，本文借鉴Koop和Korobilis[8]的方法，通过DMS方法来选择最优的FCI。根据每个模型在某时点上对Yt中主要宏观经济指标的预测表现，计算出该时点选择每个模型的概率，假设给定直到t-1期的信息，我们的目的是计算t时点选择第Mj个模型来构建最优FCI的概率为pt|t-1,j，根据Raftery等[24]、Koop和Korobilis[25]，给定初始条件p0|0,j，j=1,…,J，该概率值的状态空间预测方程可以表示为：

(7)

更新方程为：

(8)

其中，fj(Datat|Data1:t-1)为第j个模型的拟合优度；0≤α≤1为遗忘因子。

因此，一旦给定初始值p0|0,j便可利用卡尔曼滤波法估计出t时点采用模型Mj的概率值pt|t,j，从中选择概率值最大的模型所提取出的共同因子作为当期FCI值，进而根据DMS方法构建最优的FCI。

三、变量的描述与FCI的构建

(一)金融变量的选取与处理

从国内文献来看，在实际构建FCI时不同的文献所采用的金融变量具有较大差异，但也存在一些共识。其中，短期利率一般以全国银行间同业拆借市场7天同业拆借利率为代理变量，汇率一般以国际清算银行公布的人民币实际有效汇率为代理变量，股票价格一般以上证综指月末收盘价为代理变量，而房地产价格一般以国房景气指数为代理变量。因此，为与现有文献一致，本文在构建FCI时始终将以上4个变量包括在模型中。陆军和梁静瑜[14]指出，我国目前尚无一种可作为金融市场基准利率的指标，贷款利率与银行间同业拆借利率具有不可替代性，从而结合我国实际情况，在构建FCI时应考虑短期贷款基准利率。很多研究表明，我国货币政策倚重于数量型传导渠道，且货币供应量相对于产出和物价具有一定的先行性，因而货币供应量M1也应该包含进模型当中。因此，本文选取上述6个指标作为不可替代的固定变量进入模型。为避免变量选择的主观性而遗漏重要信息或者选择无关变量而影响FCI的准确性，本文参照已有的研究成果，选取了深证成份收盘指数、货币供应量M2、美元兑人民币平均汇率、国际原油价格、社会融资规模、金融机构人民币各项贷款余额、1年期固定利率国债到期收益率和7天债券质押式回购交易平均利率8个重要金融变量作为备选变量，通过DMS方法来决定它们在某期是否可以进入模型用以构建FCI。此外，在宏观变量方面选取经济一致景气指数与CPI。

各金融变量和经济变量样本期为2000年1月份至2015年11月份，数据来源于中经网统计数据库、Wind资讯金融数据库和国家统计局网站。在模型估计之前，我们先对数据进行预处理。首先利用X-12方法消除金融变量中的季节成分与不规则成分，从而得到变量趋势循环(TC)成分；其次利用HP滤波方法将趋势与循环成分分离；最后得到各金融变量的缺口[2-15]。利率类变量的缺口为实际利率与利率趋势值之差，其他变量的缺口为(变量实际值-变量趋势值)/变量趋势值。对处理后的变量进行单位根检验显示，所有金融变量均在1%的显著性水平上拒绝原假设，*限于篇幅，本文不再具体列出单位根检验结果，如有需要可向作者索取。即所有变量平稳，满足建立模型的条件。

(二)备选变量选择与分析

由于本文采用了DMS方法来挑选8个备选金融变量是否进入TVP-FAVAR模型用以构建FCI，因此，我们可以观测出每一期用以构建FCI的变量总个数。

除了6个始终包括在模型中的固定变量外，平均每期将有1—4个备选金融变量进入模型，即构建FCI的金融变量个数平均为7—10个。值得注意的是，随着2005年7月我国实行了有管理的浮动汇率以及2006年底我国股权分置改革的基本完成，2006年以后模型中的变量数目大幅度增加，并在金融危机期间达到了峰值，这表明模型在一定程度上可以刻画我国经济形势的变化，同时也暗含金融危机使得我国金融市场环境和经济环境变得更为复杂，对我国金融系统的稳定与发展产生了深远的影响。

图1刻画了另外8个备选金融变量在每一时期进入模型以构建FCI的时变概率。

图1 备选金融变量在每一期进入模型的时变概率

从图1可以看出，2007—2010年左右，社会融资规模等代表货币传导途径中信贷渠道的变量*社会融资规模指标中包括各项贷款余额的信息，因而从总体来看，金融机构人民币各项贷款余额指标进入模型的概率并不高。进入模型的概率较大，说明在此期间信贷渠道对宏观经济的运行起到了重要作用，但2011年后的作用有所下降。而在我国股权分置改革完成后，深证成份收盘指数进入模型的概率较此前明显增大，通过将该指标与通胀率作图对比发现，*限于篇幅所限，本文并未在行文中作图，如有需要可向作者索取。“股改”完成以来，深证成份收盘指数的走势先行于通胀率5个月左右，并且两者的相关性相对较高，表明该变量可以为监测物价的走势提供有益的支持。但平均而言，利率类变量和货币供应量M2进入模型的概率较低，因为这些变量与银行间同业拆借利率和货币供应量M1的走势非常接近，它们含有相似的信息，而后者始终包含在模型当中，因此，利率类变量和货币供应量M2所能提供的额外有用信息非常有限。样本期内美元兑人民币平均汇率、2007年后国际原油价格等代表国际因素变动的变量进入模型的概率较高，说明随着我国对外开放程度的不断提高与经济体制的不断完善，外部冲击对国内物价水平具有重要的影响，这也在一定程度上反映出我国货币政策传导途径中汇率渠道的重要性。

(三)FCI的构建与分析

图2描述了运用具有时变维度和时变因子载荷矩阵的TVP-FAVAR模型构建的我国新型FCI和通胀率走势。

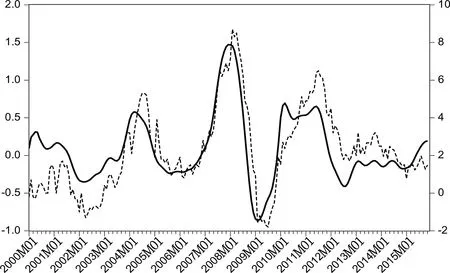
图2 新型FCI(实线，左轴)与通胀率(虚线，右轴)的相关性比较图

从图2可以看出，2003—2004年，FCI表现为从零附近逐渐上升，在此期间，我国货币供应量增速维持在20%左右的高增长阶段，央行的货币政策逐渐由稳健转变为适度宽松，总体物价水平处于温和通胀区。2007—2008年，股权分置改革的完成以及人民币升值导致的“热钱”涌入共同推动了我国股票市场的繁荣，同时房地产市场较为活跃致使房价大幅攀升，而全球市场流动性过剩也引发了输入型通胀，这些因素的共同作用使得我国进入了一轮严重通胀期，在此期间FCI走势也呈现出日益上升的态势，其值也创造出样本期间的历史峰值。2008—2009年，受全球金融危机的严重影响，我国经济增长速度和物价快速下滑，甚至出现了短暂的通货紧缩。在此之前央行实行了稳中适度从紧的货币政策，并且多次提高存款准备金率和存贷款基准利率，致使FCI呈现出快速收紧的态势，并下探至2000年以来的最低值。2009—2011年左右，前期政府为了应对国际金融危机、拉动国内经济，推出了4万亿元等一系列超常规经济刺激举措，货币供应量快速增长，信贷总量急剧增加，货币政策极为宽松，进而由流动性过剩引发经济进入新一轮温和通胀期，FCI呈现出收紧—适度—宽松的快速转变过程。2013年以来，我国面临经济“新常态”下增速放缓、结构调整和动力转换的新特征和外部环境不确定性加大的新形势，为进一步降低企业融资成本以支持实体经济增长，保持金融体系流动性合理充裕，以促进经济平稳健康发展，央行多次进行“降准降息”，货币政策取向逐渐转变为适度宽松，2015年以来FCI走势呈现出上扬态势。

由以上分析可见，本文利用时变参数和时变维度方法构建的FCI与我国宏观经济现实吻合程度较好，能够较为准确地反映我国金融市场整体运行以及宏观经济变动情况，因而可以作为宏观经济政策制定的参考指标。FCI的走势还表明，除金融危机期间外，我国宏观金融市场运行状况整体平稳，货币政策较为稳健。在下文中我们将进一步定量分析FCI与通胀率的关系。

四、FCI与通胀率的关系分析

(一)相关性分析

从图2可以看出，FCI与通胀率的走势之间具有高度的一致性，且FCI具有一定的先行性，这一点在2004年以来尤为明显。从周期峰谷对应法分析可以看出，FCI的波峰和波谷对通胀率的波峰和波谷超前效应比较明显。据此，我们可以初步认为FCI可以作为通胀率的短期先行指标以监测其未来走势。

FCI与通胀率的时差相关分析结果如表1所示，在样本期内新型FCI相对于通胀率的先行期为2—3个月，最大时差相关系数达到0.8400左右。

表1 不同先行期下FCI与通胀率的时差相关系数

为进一步分析本文构建的新型FCI的优劣，我们将其与国内权威期刊上的相关研究成果[9-13-15]进行了比较，通过表1的对比可以发现，本文构建的FCI与通胀率的相关性更高，并且对通胀率的先行性更加明显。这说明本文构建的FCI能够更早、更准确地预判通胀率未来可能发生的变动状况，从而可以为宏观调控提供更加有价值的参考。

(二)Granger因果关系分析

FCI是否能够作为货币政策操作的参考指标，还可以通过经济计量方法中的Granger因果关系检验进行考察，即FCI是否能够为预测通胀率提供有用的信息。表2列出了上文构建的FCI与通胀率之间的Granger因果关系检验结果。

表2 Granger因果关系检验结果

注：表中数值为Granger因果检验的P值。

从表2可以看出，FCI在滞后1—6阶时都能够以1%的显著性水平拒绝“FCI不是通胀率的Granger原因”的原假设，从而很有把握地说明FCI是通胀率变动的Granger原因。与此相反，除滞后1阶以外，通胀率的各阶滞后在5%的显著性水平上都不能拒绝“通胀率不是FCI的Granger原因”的原假设，这说明通胀率不是FCI变动的Granger原因，该结果进一步支持了上文中时差相关分析的结论。据此，我们可以认为存在着从FCI到通胀率的单向Granger因果关系，同样说明，上文中构建的FCI可以在短期内预测通胀率未来可能的走势。该结论也为FCI对通胀率的预测能力分析奠定了基础。

(三)FCI对通胀率的预测能力分析

根据余辉和余剑[15]以及周德才等[13]的相关研究，本文进一步使用下式的循环方程考察本文构建的FCI对通胀率的预测能力：

πt=α+βFCIt-k+ζt

(9)

其中，πt为通胀率，FCIt-k为FCI的滞后值，k的取值范围选择为0—6，ζt为误差，β为系数，α为常数。

表3列出了循环方程的预测结果。

表3 不同先行期下FCI对通胀率的预测能力

从表3可以看出，FCI在先行2个月和3个月时对通胀率的预测能力最强，其对通胀率的解释力度均达到71%以上，与时差相关分析的结果一致。从样本内拟合效果来看，FCI在先行2—3个月时效果最好，平均相对误差(MAPE)在0.95%以下，此时均方根误差(RMSE)也达到最小值，这说明在先行2—3个月左右用FCI来预测未来通胀率的可信度最高。对比模型拟合优度和RMSE发现，与国内学者已有研究相比，本文构建的FCI在预测能力方面也体现出比较明显的优势。

五、结论与启示

(一)结论

本文首先利用具有时变因子载荷矩阵的因子增广向量自回归(TVP-FAVAR)模型提取金融变量共同因子，其次借助DMS方法筛选每期的最优因子，以此构建了我国新型FCI，最后利用时差相关分析、Granger因果关系检验和预测循环方程等方法分析了构建的FCI与通胀率之间的相关关系，并将分析结果与国内现有的同类指数进行了比较。通过研究发现：基于时变参数和时变维度的TVP-FAVAR方法构建的FCI与我国宏观经济运行吻合程度较好；相对于国内现有研究成果，本文所构建的新型FCI与通胀率之间具有很强的相关性，且在短期内，这种相关性要优于现有研究中的FCI。Granger因果关系检验表明，存在从FCI到通胀率的单向Granger因果关系，并且FCI对通胀率先行性较为明显，平均先行2—3个月，说明其能够较好地预测通胀率的未来走势。以上结论说明本文所构建的FCI可以作为通胀率的先行指标以及宏观经济政策制定的参考指标。

(二)启示

第一，新型金融状况指数作为综合反映金融市场各方面信息的一个综合指数，无论是对反映金融市场整体运行情况，还是对监测和预测未来通胀率走势都具有重要作用。一些发达国家的央行和国际组织已经着手编制相应的金融状况指数或货币状况指数，因而有关研究机构或部门可结合相关学术研究和国际经验，构建能够准确反映我国金融市场整体运行情况和货币政策导向的FCI并定期公布，以期能够稳定市场预期，减少政策不确定性可能带来的经济损失，进而促进金融市场与实体经济的健康平稳发展。

第二，在构建FCI时我们发现，全球金融危机以来，反映国际因素的原油价格指数以及美元兑人民币平均汇率等指标进入模型的概率较大，因而我们应该注意国际因素对我国物价水平造成的影响，提高金融市场抵御外来风险的能力。此外，除模型中固定不变的全国银行间同业拆借市场7天同业拆借利率和短期贷款基准利率以外，利率类指标进入模型的概率较小，对物价等宏观指标的先行性不强。这也在一定程度上说明我国利率市场化虽已基本完成，但是仍需要进一步完善。

[1] Goodhart，C.，Hofmann，B.Financial Variables and the Conduct of Monetary Policy[R].Sveriges Riksbank Working Paper，2000.

[2] 栾惠德，侯晓霞.中国实时金融状况指数的构建[J].数量经济技术经济研究，2015，(4)：137-148.

[3] Goodhart，C.,Hofmann，B.Asset Prices，Financial Conditions，and the Transmission of Monetary Policy [J].Proceeding,2001,114(2):198-230.

[4] Gauthier，C., Graham，C.，Liu,Y.Financial Conditions Indexes for Canada [R].Bank of Canada Working Paper，2004.22.

[5] Angelopoulou，E.，Balfoussia，H., Gibson，H.D.Building a Financial Conditions Index for the Euro Area and Selected Euro Area Countries: What Does It Tell Us About the Crisis? [J].Economic Modelling，2014，38(38)：392-403.

[6] Hatzius，J.,Hooper，P.，Mishkin，F.S.，Schoenholtz，K.L., Watson，M.W.Financial Conditions Indexes: A Fresh Look After the Financial Crisis[R].NBER Working Paper，2010.

[7] Matheson，T.D.Financial Conditions Indexes for the United States and Euro Area [J].Economics Letters, 2012，115(3)：441-446.

[8] Koop，G., Korobilis，D.A New Index of Financial Conditions [J].European Economic Review，2014，71(1)：101-116.

[9] 戴国强，张建华.中国金融状况指数对货币政策传导作用研究[J].财经研究，2009，(7)：52-62.

[10] 陆军，刘威，李伊珍.新凯恩斯菲利普斯曲线框架下的中国动态金融状况指数[J].财经研究，2011，(11)：61-70.

[11] 封思贤，蒋伏心，谢启超，等.金融状况指数预测通胀趋势的机理与实证[J].中国工业经济，2012，(4)：18-30.

[12] 徐涤龙，欧阳胜银.金融状况指数的理论设计及应用研究[J].数量经济技术经济研究，2014，(12)：55-71.

[13] 周德才，冯婷，邓姝姝.我国灵活动态金融状况指数构建与应用研究[J].数量经济技术经济研究，2015，(5)：114-130.

[14] 陆军，梁静瑜.中国金融状况指数的构建[J].世界经济，2007，(4)：13-24.

[15] 余辉，余剑.我国金融状况指数构建及其对货币政策传导效应的启示[J].金融研究，2013，(4)：51-60.

[16] 肖强，司颖华.我国FCI的构建及对宏观经济变量影响的非对称性[J].金融研究，2015，(8)：95-108.

[17] 王维国，王霄凌，关大宇.中国金融条件指数的设计与应用研究[J].数量经济技术经济研究，2011，(12)：115-131.

[18] 邓创，徐曼.中国的金融周期波动及其宏观经济效应的时变特征研究[J].数量经济技术经济研究，2014，(9)：75-91.

[19] Boivin，J.,Ng，S.Are More Data Always Better for Factor Analysis? [J].Journal of Econometrics，2006，132(1)：164-149.

[20] Koop，G.,Korobilis，D.Large Time-Varying Parameter VARs [J].Journal of Econometrics，2013，177(2) ：185-198.[21] 郭永济，丁慧，范从来.中国通货膨胀动态模型预测的实证研究[J].中国经济问题，2015,(5)：3-35.[22] Paries，M.D.，Maurin，L.,Moccero，D.Financial Conditions Index and Credit Supply Shocks for the EURO [R].European Central Bank Working Paper No.1644，2014.

[23] Wacker，K.M.，Lodge，D.,Nicoletti，G.Measuring Financial Conditions in Major Non-Euro Area Economies [R].European Central Bank Working Paper,2014.

[24] Raftery，A.E.，Karny，M.，Ettler，P.Online Prediction Under Model Uncertainty Via Dynamic Model Averaging: Application to a Cold Rolling Mill[J].Technometrics，2010，52(1)：52-66.

[25] Koop，G.，Korobilis，D.Forcasting Inflation Using Dynamic Model Averaging[J].International Economic Review，2012，53(3)：867-886.

(责任编辑：巴红静)

2017-02-19

国家社会科学基金重大项目“新常态下我国宏观经济监测和预测研究”(15ZDA011)；国家自然科学基金项目 “基于非参数方法和非线性模型的经济景气和通货膨胀监测预警研究”(71173029)；辽宁省特聘教授(2012)项目

陈 磊(1963-)，男，吉林人，教授，博士,博士生导师，主要从事经济周期波动、金融与宏观经济分析和预测以及数量经济学等方面的研究。E-mail：chenlei@dufe.edu.cn 咸金坤(1991-)，男，山东临沂人，硕士研究生，主要从事宏观经济分析与预测、经济周期波动等方面的研究。E-mail：xianjk@126.com 隋占林(1986-)，男，河北保定人，博士研究生，主要从事宏观经济分析与预测、经济周期波动等方面的研究。E-mail：suizhanlin@163.com

F832.0

A

1000-176X(2017)06-0035-08