寻根溯源,在挖掘定律原型中渗透建模思想
2017-07-06袁玉梅
袁玉梅

摘 要:“乘法分配律”作为一种数学模型,是学生最难理解和掌握的。究其原因,主要是学生没有从根本上理解乘法分配律的真正意义;在教学过程中,要加强对教材定律“原型”的挖掘,要强化并设计学生所需要的“活动经验”渗透。如果我们在教学乘法分配律之前能够对教材有一个完整准确的把握,以让活动的经验在学习的过程中充分发挥作用,并在实际教学中提早形成定律的模型,适当提前定律教学的话,一定会取得较好的效果。
关键词:乘法分配律;建立模型;运算能力
“乘法分配律”在小学数学的内容体系中,是以数学知识与数学模型的形式存在的。通常情况下,它与乘法交换律及结合律并不完全相同,因而在小学生进行学习的时候,存在着不少的难点需要突破。运用乘法分配律进行简便运算历来都是学生比较头痛的问题,虽然许多老师都在教法上下了很大的工夫,但收效并不理想。
反思学生的学习过程,笔者以为学生遇到学习障碍的主要原因在于:第一,学生对乘法分配律的理解还只停留在表面形式上,没有从根本上理解乘法分配律的真正意义;第二,部分教师在教学过程中没有利用好教材,尤其是没有利用好教材设计这一内容的思想,从而让学生的原有活动经验难以发挥作用,而本内容的原型也就没有有效呈现。因此,即使学生通过一定量的训练做对了基本类型的题目,但遇到变式题时,也往往错误连连。那么,什么样的教学过程,才能让学生在建构这一知识的时候,能够真正走出机械模仿的怪圈,从而让他们的学习过程更加有效呢?笔者以为如果我们在学习乘法分配律之前有效地研究教材,有效地帮学生建构出乘法分配律所需要的经验及模型,适当提前定律教学的话,一定会取得较好的效果。
一、系统把握教材,铺垫好基础知识,在前期学习中塑立乘法分配律的模型
很多教师在备课过程中都不会主动去关注学生学习某个知识的出发点,更有甚者,是课上完了之后才根据学生作业中出现的问题,发现自己在教学中存在的不足,或者是说发现了教材的某个环节并不适合学生的实际学习需要。如果我们在学期初就先对本学期涉及的数学知识进行寻根溯源,认真研读教材的真正用意,系统地把握教材后再进行备课,提前铺垫基础知识,并在教学过程中有意识地为学生的后续学习打下坚实基础的话,一定会取得较好效果。
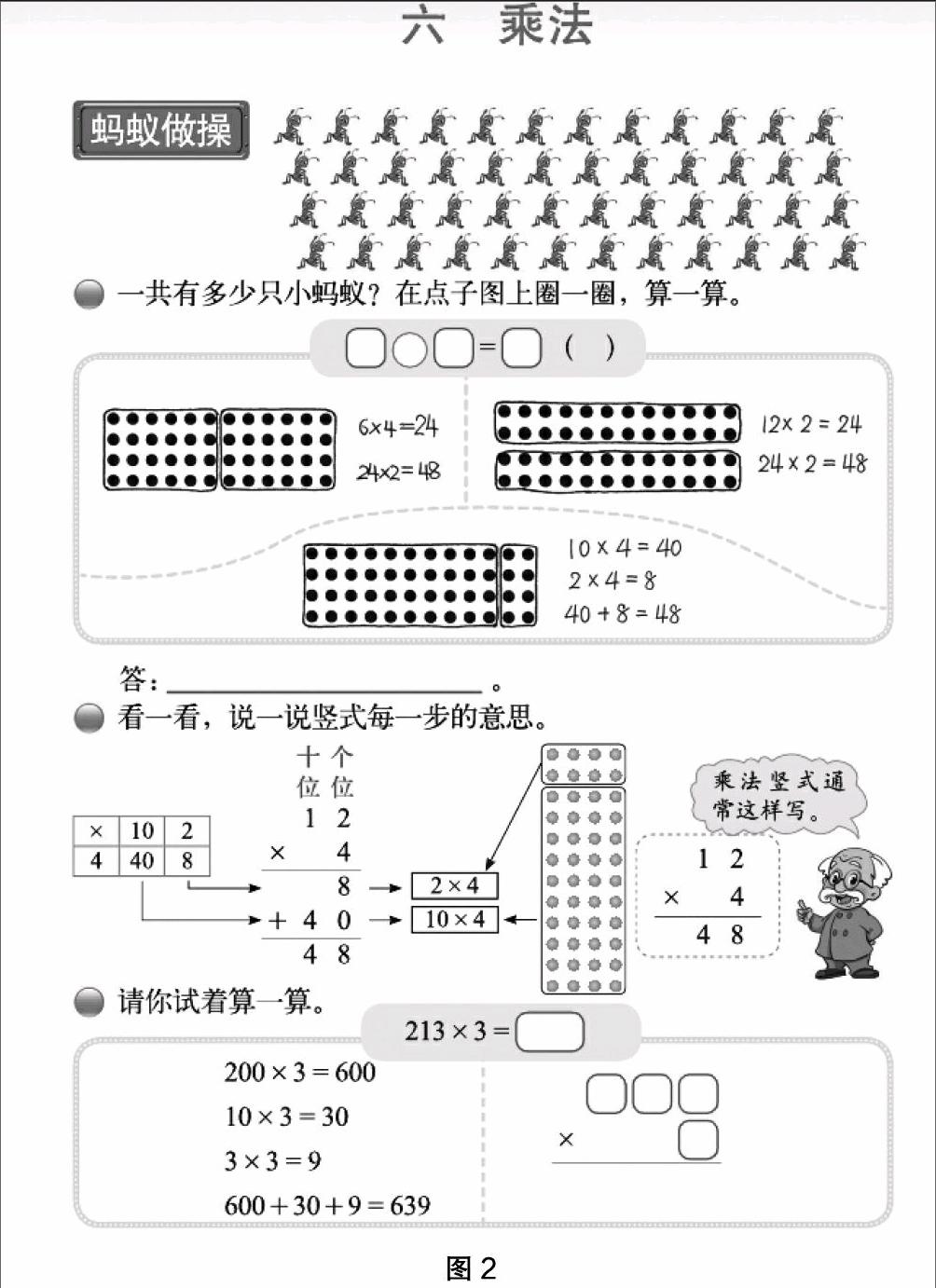
北师大版小学数学教材在这一方面的编排就比较好。为分解乘法分配率及其运用这一教学难点,教材从二年级学习乘法口诀开始就提前做了一些渗透。如第三册第78页《6的乘法口诀》中是这样设计的,如图1。
教材这样的设计本身是为6的乘法口诀做巩固,同时也期待学生在有效理解学习内容的基础上,为乘法分配率奠定学习的基础。如果读懂了教材的编排意图,在开展教学的过程中就可以最大限度地发挥这些习题的多重价值了。浈江区教研室的邓莹源老师在执教这一课时就给我们做了很好的示范。
课伊始,邓老师就先让学生复习2~5的乘法口诀及其表示的意义(即乘法口诀解决的是几个几相加的问题),然后再从2~5的乘法口诀中提出与6有关的4句口诀(二六十二、三六十八、四六二十四、五六三十)进行进一步研究。邓老师先让学生根据6的口诀分别说出两个乘法算式和算式表示的意义,然后从乘法口诀表示的意义入手引导学生观察:2个6与3个6之间有什么样的联系呢?学生在讨论后发现3个6比2个6多1个6。在此基础上邓老师要求学生用算式表示出这一发现:即3×6=2×6+6。接下来邓老师又引导学生思考:这个发现在6的其他口诀中是否也能找到呢?很快学生就在观察、比较、推理后发现6的乘法口诀中相邻两句口诀之间都存在这样的规律:即相邻两句口诀中后一句口诀比前一句口诀多6。在学生都已经熟练掌握这一规律后,邓老师便鼓励学生用这种方法去编排出6的其他乘法口诀。在这一过程中,邓老师引导学生从理解6的乘法口诀的意义入手,既帮助学生理解了口诀,又逐渐建立了乘法分配律的初步模型,累积了数形结合的思想。还促进了思维发展,为学生的后续学习打下坚实的基础。
二、在学习情境中理解拆分,为建构乘法分配律的模型思想提供基础
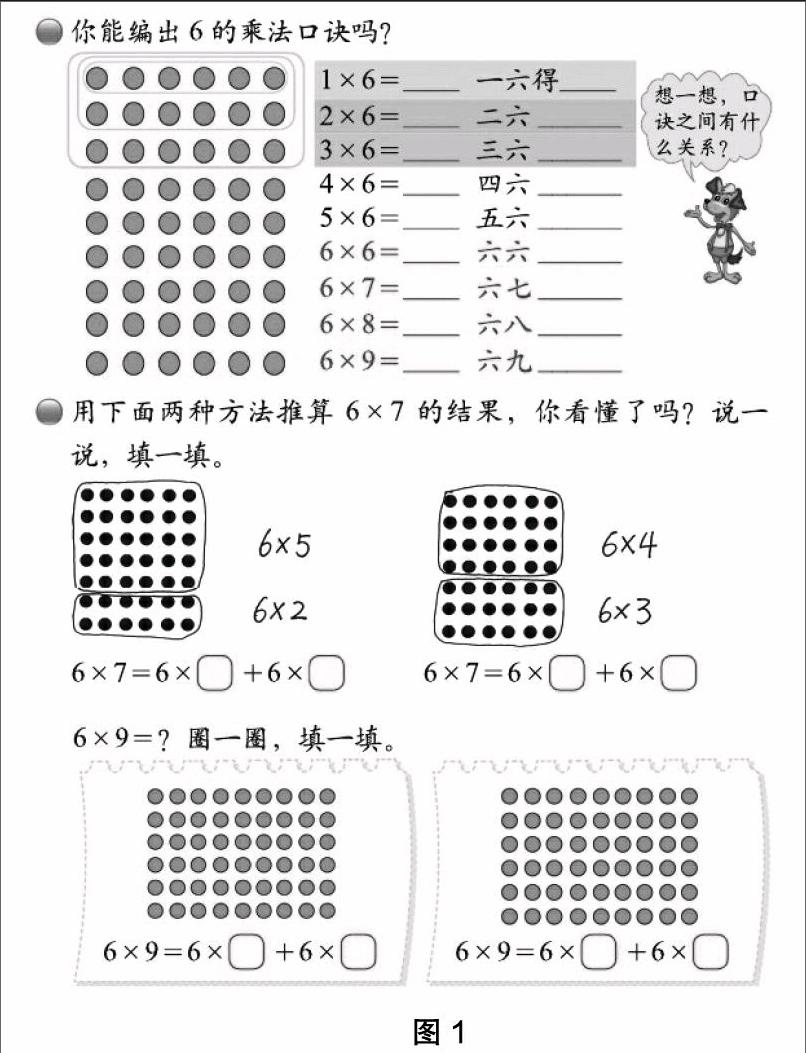
在以往的学习中,学生在运用乘法分配率进行简便运算的过程中遇到的最大障碍就是对数的拆分不能适应,缺少把四个数参与的运算改变成三个数的运算(或者反过来:把三个数的运算转变成四个数的运算)的经验。他们还停留在原来是几个数,现在还应该是几个数的经验中,不习惯这种变化。北师大版在教材编排上就关注到了这一点。如第五册《笔算乘法》第52页,如图2。
在学习《两三位数乘一位数的笔算乘法》时,教材安排了三种不同形式的解题方法来计算12×4:画点子图口算、列表拆分计算和竖式笔算。仔细观察这三种计算方法,其实计算的过程都是一样的,只不过计算形式不同。其实在这里就已开始为乘法分配率铺垫了“把一个数拆分成两个数相加的和”的经验。
笔者在执教这一内容时先让学生借助点子图圈一圈,把点子图进行拆分后再进行计算。在拆分过程中,笔者发现大多数学生都会把12拆成10+2,但是也有一些同学把12拆成6+6或6×2,再分别与4相乘,最后再把两次相乘的结果合在一起。还有的同学没有拆12这个数,而是把4拆成了2+2或2×2,再分别与12进行相乘。无论如何拆分,学生在这一过程中,都获得了拆数的经验。在多种拆分方法出来以后,适当进行优化,根据具体的算式再渗透一下凑整的策略,会取得更好的效果。因此,在点子图圈画以后,笔者又引导学生完成列表法。学生在进行列表计算的过程中通过对比,优化出了凑整的策略。最后结合口算、点子图和表格的方法探究出了乘法竖式的计算方法,就是用一位数分别去乘另一个乘数的每一位,再把所得的积相加。这节课学生在“拆——算——合”的过程中较好地理解了拆分,为乘法分配律的“建模”做好强有力的铺垫。
三、提前“塑型”,在生活中寻找定律“痕迹”,为乘法分配律做好孕伏
在学习长方形的周长时,笔者进一步引导学生发现,原来这个知识的学习中就蕴含着乘法的分配律。如果我们在这里对这个知识的学习过程进行进一步研究,并适当挖掘教材潜力, 给乘法分配律建立学生熟知的几何模型的话,能为今后学习乘法分配律打下基础。
如图3是“长方形的周长”(北师大版第五册第48页)部分内容。
在教学这一内容时,笔者先鼓励学生用不同的方法进行解答,待出现以上三种算法后,再比较这几种方法的异同,延长学生体验和经历的过程。特别是在比较“5×2+3×2”与“(5+3)×2”的过程中就已经提前为乘法分配律进行了“塑型”。经过多次的解答,学生最后都选择了比较简便的算法。这时笔者才让学生去想办法总结刚才的学习过程,尤其是长方形周长公式的建立过程。这个过程虽然要花费一定的时间,但是学生的学习经验也是在这个时间中积累起来的,因此这个时间的花费是值得的。尤其是考虑到这一经验的积累对后面知识的学习也有帮助,其可让这一知识的教学难点迎刃而解。
刘加霞教授曾说过“把握数学的本质是一切教学法的根”。通过乘法分配律的教学,笔者对这句话有了更深刻的理解。进一步讲,数学教师只有理解并把握了数学的本质,才能以有效的眼光审视自己的課堂,从而提高自己的教学水平。
