运动中发展直观,直观中培育素养
2017-07-06潘光志
潘光志

摘 要:“几何直观”是新课标十大核心概念之一,其发展有助于学生了解图形的特征,形成对图形的敏锐洞察力。对数学思维的深刻理解,会将学生引向深度的数学学习与探究。在“图形与空间”领域的教学中,让图形“运动”起来,换一个视角认识图形,能帮助学生认识到图形本质、拓展学生的空间维度、形成新的知识网络,从而发展其几何直观,培养学生形成创新型思维方式,对于培养学生的实践创新能力(核心素养之一)将起到重要的作用。
关键词:小学数学;图形运动;几何直观;核心素养
2016年9月《中国学生发展核心素养》正式出炉,核心素养以培养“全面发展的人”为核心,分为文化基础、自主发展、社会参与三个方面,综合表现为人文底蕴、科学精神、学会学习、健康生活、责任担当、实践创新六大素养,具体细化为国家认同等18个基本要点,暂时还没有对数学学科提出具体的育人目标和任务。但笔者经过对其内容的研读,发现新课标中提出的十大数学核心概念,与核心素养之间有着千丝万缕的联系。十大核心概念包括:数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识。以“几何直观”为例,就是落实核心素养的重要抓手,特别是对于“实践创新”这一素养的培养有着重要的作用。
“几何直观,即利用图形描述与分析问题”,这是新课标中对其作用的说明,其实它的意义远不止于此。它与空间观念有所不同,更强调借助一定的直观背景条件进行整体把握的能力。几何直观能力有助于学生对数学思维的深刻理解,将学生引向深度的数学学习与探究。更重要的是,其是一种发现问题的能力、研究问题的策略,凭借直观的载体,简捷、巧妙地化解问题,能成为学生创新型思维的开端。几何学(空间与图形)是研究图形及其关系的内容,几何直观在几何教学中无处不在,但通常都是对静止的图形进行研究,图形的本质及其关系往往得不到深度揭示,对学生几何直观的发展有一定的阻碍。让图形“动起来”,从运动的视角研究图形,能帮助学生对图形进行更深入的认识与探究。
一、“运动中”认识图形本质
在认识图形时,小学教材中大多用例子来说明:“像这样的图形就是……”,没有给出文字的描述或定义。这样的编写符合小学生的年龄特点与思维发展水平,但笔者认为教学中不应止步于此,要将图形的静态或动态定义向学生渗透与介绍,使学生触碰图形的本质,特别是某些图形的动态定义的渗透,是解决教学难点、发展学生几何直观的重要途径。
案例1 《角的初步认识》(新人教版二年级上册)
【教学片段】
教师首先请学生闭上眼睛摸一摸圆形、三角形和长方形,让学生感受“角是尖尖的”这一外部表征,然后让学生找出生活中的角,抽象出角的形象。以上教学过程,看上去进行得很顺利,但在接下来的画角的学习中,学生却出现了不少的错误。有的将三角形当作角画出来,有的先画了两条边,却怎么也凑不成一个角。教师不停地指导学生画角的顺序(即先画顶点,再画边),却收效甚微。
【案例评析】
以上问题的产生,主要在于教学中对角的本质属性的忽略。角有两种定义:静态定义是“具有公共端点的两条射线组成的图形叫作角”;动态定义是“一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形叫作角”。其中静态定义中“射线”一词本身也具有动态的表征。教师应将这两种定义在课堂上加以渗透。
如图1,先展示激光束有关图片,再在黑板上模拟图1中角的形成过程,即先画顶点,再从这点出发,画两条射线。通过图片展示与教师的画角,向学生渗透角的静态定义,使学生对角的“点出发的线”这一运动形成过程有所感受,对学生掌握画角与比较角的大小能起到很大作用,更有助于学生对角这一图形的深刻理解。
教师还可利用扇子的开合模拟角的另一动态形成过程(如图2),渗透角的动态定义。固定扇子的一边,将另一边进行旋转,形成大小不一的角。此过程同时对学习角的大小比较、角的分类都有着积极的作用。更重要的是,通过两种动态形成角的过程比较,学生会发现无论哪种运动,“角”都脱离不了“一个顶点”与“两条边”这两大要素,实现了对“角”这一图形表征与本质的深刻理解,有利于学生今后探索与角有关的更复杂的内容,如数复杂图形中角的个数、三角形有关问题等。
类似的,还有“圆的认识”。圆可以看作是“到定点的距离等于定长的点的集合”。在教学用圆规画圆时,向学生提问:为什么圆规能画出圆来?渗透:圆规画出的每一个点到圆心的距离都相等,这些点运动的轨迹就形成了圆。在画圆的运动中,体会动态的圆的形成过程,使学生对“点动成线”形成感性的认识,也从中体会到极限思想等数学思想方法,促进了学生高级思维的发展,对学生的创新能力也是一种锻炼。
二、“运动中”突破空间维度
案例2 《圆柱的认识》(新人教版六年级下册)
【教学片段】
此节课,教师设计了三次图形的运动:
第一次,在学生认识“圆柱”这一名词与生活中的圆柱后,教师拿出了一个折叠灯笼(如图3),问:“这里有没有圆柱?可以变出多少个圆柱?”学生对灯笼进行拉伸,逐渐开始感受圆的垂直移动形成圆柱的过程。教师再用电脑动态演示圆上下垂直移动形成圆柱的过程,并由此介绍圆柱的底面、高等组成部分及圆柱的特征。
第二次,请学生思考:圆上下垂直平移可以形成圆柱,那长方形的运动可否形成圆柱呢?学生动手实践,对长方形进行旋转、围拢等操作,以形成大小不一又互有关系的圆柱。
第三次,动画演示:点动成直线——直线卷曲成圆——拉直直线——直线平移成平面——平面卷曲成圆柱的侧面。
【案例评析】
在以上的教学中,教师引入图形的运动,使学生认识到:高维的图形可以由低维的图形运动变化得到。通过这个过程,帮助学生打通了低维到高维图形变迁的通道,拓展了学生认识世界的空間维度。借助低维的图形的变化,能更加深入地了解高维图形的特征,为理解立体图形的特征、算法等开辟了一条新的道路。
第一次运动,用圆的垂直移动得到圆柱,得到其垂直移动的路径其实就是圆柱的高,所以圆柱的高一定是垂直于底面的。而且根据圆柱,学生跟着想到:长方体也可以看成是由长方形上下垂直平移得到的。至此,就形成了图形算法的统一:圆柱的体积可看作底面圆的面积乘其垂直移动的距离。长方体的体积可看作底面长方形的面积乘其垂直移动的距离(即高)。学生可以从中得出直柱的体积统一公式:底面积乘高。
第二次运动,用长方形旋转、围拢等方法得到圆柱。学生在课后更自己尝试用梯形旋转、三角形旋转等方式得到其他立体图形。经历另一种运动方式实现从二维到三维的转化,对于后续认识圆锥、球等都有很大的帮助。
第三次运动,将“点动成线”“线动成面”“面动成体”进行系统的演示,不但向学生渗透了“转化”的数学思想方法,而且用动态的方式将三个维度的空间进行展示,为学生学习与解决图形类问题提供了新的思路。
三次运动,各有重点,各有作用,又相互补充。总的来说,是用一种全新的视角带领学生拓展了空间维度,发展了学生的几何直观,培养了学生的创新精神。
三、“运动中”编织知识网络
案例3 《多边形面积单元复习》(新人教版五年级上册)
【教学片段】
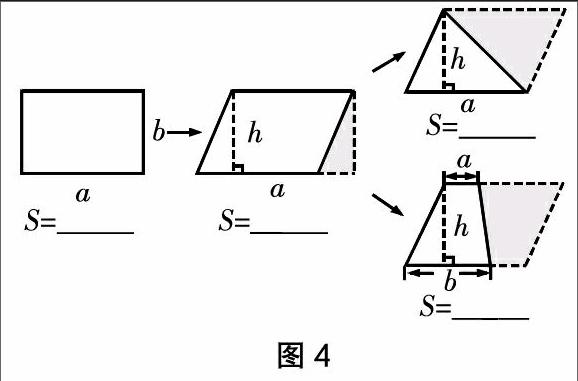
学生根据书本的提示,找出多边形面积之间的关系(如图4)。
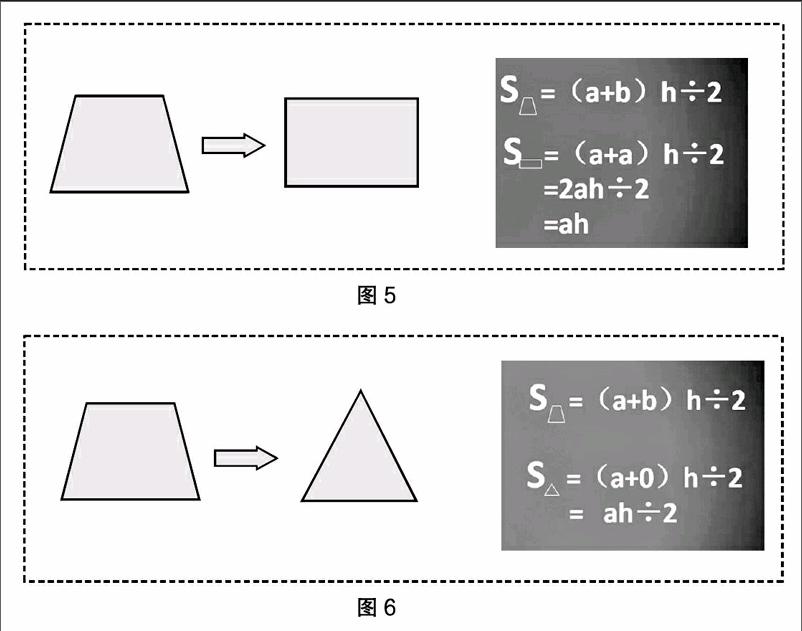
接下来,教师用动画的形式,向学生演示图形之间的联系。将梯形的上底两端点拉开,使得上底与下底相等,变成了长方形,由此可以反推出长方形的面积公式(如图5)。将梯形上底两端点拉近成一点,变成了三角形,由此又可反推出三角形的面積公式(如图6)。
【案例评析】
上例中,运用图形中部分元素的运动,将图形进行变形,形成与其他图形的联系。这种变形与以往剪拼的方式有所不同。剪拼是改变了图形的形状,但没有改变其面积大小,也就是形变量不变。上例中的运动虽然看上去量与形都发生了变化,但却将计算方法进行了规一,将三种图形,甚至是四种图形的面积计算归为一种。这样的知识网络构建是对教材的补充与拓展,为学习中学的“动态几何”孕伏了线索,更体现了“化繁为简”的几何直观的价值,有助于学生创造性思维的发展。
让图形“动起来”,能让学生对图形的认识更加深刻,更能把握图形的特征及图形之间的关系,其想象力、推理能力、反思能力也得到了发展。只要对图形的本质及联系有了更深的认识,学生就能更好地完成凭借图形对数学对象的思考,发展几何直观,逐渐使几何直观内化为数学学习的一种思考方式与学习方式,使直观变成数学发现的向导,落实“实践创新”这一核心素养的培养。
