电磁感应热点考题预测

■北京市丰台二中 公衍录(特级教师)

电磁感应热点考题预测

■北京市丰台二中 公衍录(特级教师)

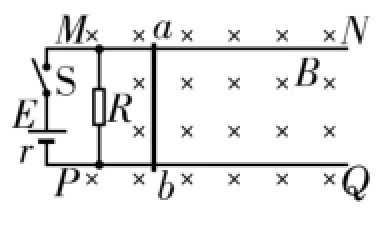
图3

图4

电磁感应能够综合高中物理的大部分内容,故近几年来高考全国卷的两道必做计算题之一便是涉及电磁感应的综合题。预计2017年的两道必做计算题中也将会有一道题是涉及电磁感应的综合题,且可能被考查的热点题型如下。

一、电磁感应与动力学综合的问题

求解电磁感应与动力学综合的问题时,必然涉及电路问题,因此求解此类问题的步骤与求解“电磁感应中的电路问题”的步骤相似,只是还需要应用牛顿运动定律、力的平衡条件等力学规律。

如图1所示,在竖直向下的磁感应强度为B的匀强磁场中,两根足够长的平行光滑金属轨道MN、PQ固定在水平面内,相距为L。一质量为m的导体棒ab垂直于轨道放置,与轨道接触良好。轨道和导体棒的电阻均不计。

(1)如图2所示,若轨道左端M、P间接一阻值为R的电阻,导体棒在水平向右的恒力F作用下由静止开始运动。求经过足够长时间,导体棒所能达到的最大速度的大小。

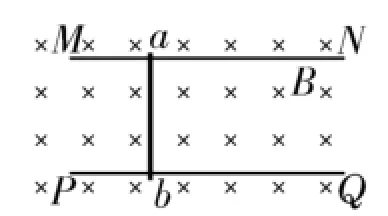
图1

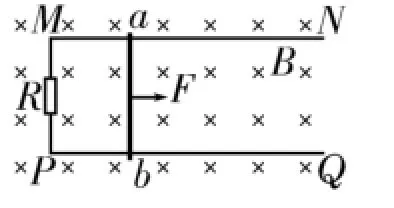
图2

(2)如图3所示,若轨道左端M、P间接一电动势为E、内阻为r的电源和一阻值为R的电阻。闭合开关S,导体棒从静止开始运动。求经过足够长时间,导体棒所能达到的最大速度的大小。

(3)如图4所示,若轨道左端M、P间接一电容为C的电容器,导体棒在水平向右的恒力F作用下从静止开始运动。求导体棒在运动过程中的加速度的大小。

(2)闭合开关S后,导体棒在安培力的作用下,向右做加速运动。导体棒因切割磁感线产生与原电流方向相反的感应电动势,导体棒中的电流减小。当导体棒产生的感应电动势与电阻R两端的电压相等,即U=BLv2时,导体棒中的电流减小为零,导体棒不再受安培力,达到最大速度。此时由电阻R与电源组成回路中的电流,电阻R两端的电压U=IR,解得

(3)导体棒向右加速运动,设在极短时间Δt内,速度的变化量为Δv,由加速度的定义得a=,导体棒产生的感应电动势变化量ΔE=BLΔv。电容器的电压等于导体棒产生的感应电动势,故电容器获得的电荷量Δq= CΔU=CΔE,由电流的定义得I=。导体棒受到的安培力F安=BIL,由牛顿第二定律得F-F=ma,解得

点评:本题第(1)问是“因动生电”,其本质属于发电机。该问表明闭合回路中的导体棒在恒定外力作用下,由静止开始做切割磁感线运动时,导体棒做变加速运动,其加速度逐渐变小,速度逐渐变大,当加速度为零时,速度达到最大,以后保持不变(具有恒定的收尾速度)。本题第(2)问是“因电生动”,其本质属于电动机。该问表明通电导体棒因为受安培力在磁场中做切割磁感线运动时,将产生与原电流方向相反的电动势(反电动势),该反电动势使得导体棒受到的安培力变小,当安培力减小为零时,导体棒将做匀速运动。本题第(3)问是“因动生电”,其本质属于发电机。该问表明回路中有电容器时,闭合回路中的导体棒由静止开始在恒定外力作用下,做初速度为零的匀加速直线运动。

如图5甲所示,水平面内直角坐标系的第一象限中有磁场分布,磁场方向垂直于水平面向下,磁感应强度大小沿y轴方向不变,沿x轴方向与坐标值x的关系如图5乙所示(图像是反比例函数图像)。顶角θ =45°的光滑金属长直导轨OM、ON固定在水平面内,ON与x轴重合,一根与ON垂直的长导体棒在水平向右的外力F作用下在导轨上向右滑动,导体棒始终与导轨接触良好。已知t=0时刻,导体棒处于原点O位置,导体棒的质量m=2kg,导轨OM、ON在原点O处的接触电阻R=0.5Ω,其余电阻不计。回路中产生的感应电动势E与时间t的关系如图5丙所示(图像是过原点的直线)。求:

图5

(1)t=2s时刻通过导体棒的电流I2的大小。

(2)1s～2s时间内回路中通过的电荷量q的大小。

(3)导体棒在滑动过程中所受水平外力F与横坐标值x的关系式。

解析：(1)由E-t图像是过原点的直线可知,当t=2s时

(3)由θ=45°可知,任意时刻t回路中导体棒的有效切割长度L=x,则导体棒产生的感应电动势E=BLv=Bxv。由B-x图像是双曲线得Bx=1(T·m),又有E=3t(V),所以v=3t(m/s),即导体棒做的是匀加速直线运动,且加速度大小a=3m/s2。由F安= BIL,,L=x,v2=2ax,F-F安= ma,解得F=F安+ma=26x+6(N)。

二、电磁感应中的功能关系和能量守恒问题

在电磁感应中用到的功能关系主要有:克服安培力做的功等于电能的增加;在纯电阻电路中,克服安培力做的功等于电热;除重力、弹簧弹力以外,其他力(包括安培力)所做的功等于机械能的增量。如图6所示,固定的水平光滑金属导轨间的距离为L,左端接有电阻R,匀强磁场的方向竖直向下,磁感应强度大小为B,质量为m的导体棒与固定弹簧相连,垂直于导轨放置,导轨与导体棒的电阻均可忽略。初始时刻,弹簧恰好处于自然伸长状态,导体棒具有水平向右的初速度v0。导体棒在沿导轨往复运动的过程中,始终与导轨垂直并保持良好接触。求:

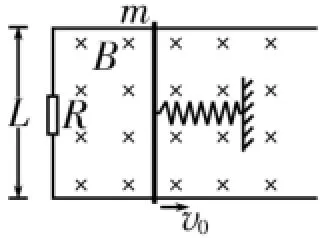
图6

(1)初始时刻导体棒受到的安培力F安。

(2)若导体棒的速度第一次为零时,弹簧的弹性势能为Ep,则在导体棒从开始运动到其速度第一次为零的过程中,安培力所做的功W1和电阻R上产生的焦耳热Q1分别为多少?

(3)导体棒最终将静止于何处?在导体棒从开始运动到最终静止的过程中,电阻R上产生的焦耳热Q为多少?

解析：(1)初始时刻导体棒产生的感应电动势E=BLv,回路中的感应电流,导体棒受到的安培力方向水平向左。

(2)在导体棒从开始运动到其速度第一次为零的过程中,由功能关系得W1=Ep-。在纯电阻电路中,电热等于克服安培力做的功,即

(3)由平衡条件知导体棒最终将静止于初始位置。由能量守恒定律得

三、涉及电路、动力学、功和能等知识的电磁感应综合问题

如图7所示,两根相距为l的光滑平行金属导轨位于同一水平面(纸面)内,其左端接一阻值为R的电阻。一与导轨垂直的金属棒置于导轨上,在电阻、导轨和金属棒中间有一面积为S的区域,该区域中存在垂直于纸面向里的均匀磁场,磁感应强度大小B1随时间t的变化关系为B1=kt,式中k为常量。在金属棒右侧还有一匀强磁场区域,该区域左边界MN与导轨垂直,磁感应强度大小为B0,磁场方向也垂直于纸面向里。某时刻,金属棒在一外加水平恒力的作用下从静止开始向右运动,在t0时刻恰好以速度v0越过边界MN,此后向右做匀速运动。金属棒与导轨始终相互垂直并接触良好,它们的电阻均忽略不计。求:

(1)在0～t0时间内,通过电阻R的电荷量的绝对值。

(2)在t(t〉t0)时刻金属棒所受外加水平恒力的大小。

(3)在0～t0时间内,回路中产生的热量。

(4)若在t(t〉t0)时刻撤去外加水平恒力,同时面积为S的圆形区域中的磁场停止变化,求金属棒还能再向前运动的位移大小x。

解析：(1)在金属棒越过边界MN之前, t时刻穿过回路的磁通量Φ=B1S=ktS。设在t到t+Δt的时间内,穿过回路的磁通量的变化量为ΔΦ,通过电阻R的电荷量为Δq,则由法拉第电磁感应定律得E=,由闭合电路欧姆定律得I=,由电流的定义得I=,解得Δq=Δt。因此在0～t时0间内,通过电阻R的电荷量的绝对值为

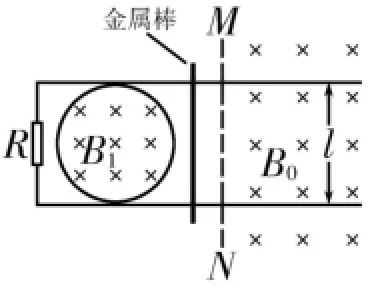
图7

(2)当t〉t0时,金属棒已越过边界MN。设外加水平恒力为f,安培力为F,回路中的电流为I,则F=B0Il,f=F。因为B1随时间的增大而变大,所以由楞次定律知在回路中产生沿逆时针方向的感生电动势,由法拉第电磁感应定律得感生电动势的大小E1=1S=kS。金属棒在边界MN右侧做切割磁感线运动时,由右手定则知在回路中产生沿逆时针方向的动生电动势,其大小E2= B0lv0。回路中总的感应电动势大小Et=又有解得

(4)选水平向右为正方向,对金属棒应用动量定理得-B0¯Il·t=0-mv0,又有¯I=解得

点评:如果某一时刻穿过回路的磁通量既包括因磁场变化产生的磁通量,还包括因导体切割磁感线而增加或减少的磁通量,则用法拉第电磁感应定律求出的感应电动势就既包括感生电动势还包括动生电动势。

(责任编辑 张 巧)