抛物线一组结论的证明与应用

■浙江省江山市第五中学 徐洪军

抛物线一组结论的证明与应用

■浙江省江山市第五中学 徐洪军

抛物线有很多优美的结论,在平时的学习中,同学们要能够灵活应用。下面,笔者通过抛物线一组结论的证明与应用来进一步揭示抛物线的本质。

结论1 已知直线l经过抛物线C:y2= 2px(p〉0)的焦点F,直线l与抛物线C交于A(x1,y1),B(x2,y2)两点,则y1·y2=

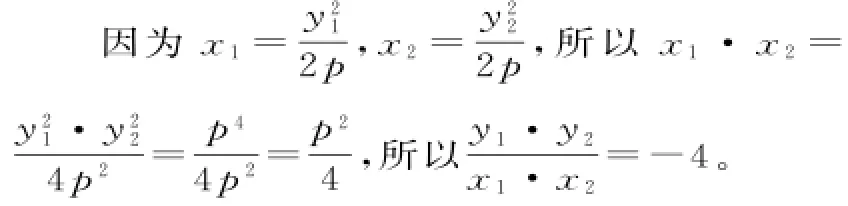
应用1 已知直线l经过抛物线C:y2= 8x的焦点F,直线l与抛物线C交于A(x1, y1),B(x2,y2)两点,则:

(2)根据抛物线的结论1可得x1·x2=因为x1〉0,x2〉0,所以

(3)根据抛物线的结论1可得y1·y2= -p2=-16。因为y1·y2〈0,所以|16y1-25y|=16|y|+25|y|≥160,当且仅当16|y1|=25|y2|=80,即y1= 5,y=-或y=-5,y=时,取等号,因此|16y1-25y2|的最小值为160。

结论2 已知直线l与抛物线C:y2= 2px(p〉0)交于A(x1,y1),B(x2,y2)两点,且满足y1·y2=-p2,则直线l经过抛物线C的焦点。

证明：(1)当x1=x2时,有|y1|=|y2|。

因为y1·y2=-p2,所以|y1|=|y2|= p,于是因为抛物线的焦点F的坐标为,所以直线l经过焦点F。

应用2 已知直线l与抛物线C:y2=8x交于A(x1,y1),B(x2,y2)两点,且满足y1· y2=-16,则直线l经过定点。

证明：因为p=4,y1·y2=-16,所以y1·y2=-p2。根据抛物线的结论2可知,直线l经过抛物线的焦点F(2,0)。

结论3 已知F是抛物线C:y2=2px (p〉0)的焦点,直线l与抛物线C交于A、B两点,记直线FA、FB的斜率分别为k1、k2,若直线l经过点,则k+k=0。

证明：设A(x1,y1),B(x2,y2),由题意可设直线l的方程为,把直线l的方程代入抛物线方程y2= 2px,消去y整理可得k2x2+(k2p-2p)x+

因为k≠0,且Δ=(k2p-2p)2-k4p2= 4p2(1-k2)〉0,所以-1〈k〈0或0〈k〈1。

应用3 已知F是抛物线C:y2=12x的焦点,直线l:y=k(x+3)与抛物线C交于A、B两点,记直线FA、FB的斜率分别为k、k,则=____。

解析：由题意可知,抛物线焦点为F(3, 0),直线l恒过定点(-3,0),根据抛物线的结论3可得,k+k=0,于是

结论4 已知F是抛物线C:y2=2px (p〉0)的焦点,斜率存在的直线l与抛物线C交于A、B两点,记直线FA、FB的斜率分别为k1、k2,若k1+k2=0,则直线l恒过定点

证明：由题意可设直线l的方程为x= my+t,其中m≠0。把直线l的方程x= my+t代入抛物线方程y2=2px,消去x得y2-2mpy-2pt=0,由Δ=4m2p2+8pt= 4p(m2p+2t)〉0,可得m2p+2t〉0。

应用4 已知F是抛物线C:y2=32x的焦点,斜率存在的直线l与抛物线C交于A、B两点,记直线FA、FB的斜率分别为k1、k2,若k1+k2=0,则直线l经过定点。

证明：根据抛物线的结论4可知,直线l经过定点(-8,0)。

在设直线方程时,要注意考虑直线的斜率不存在的情况是否满足题意。有时,也可以把直线方程设成x=my+t的形式来避免复杂的运算,进一步提高解题的准确率。

(责任编辑 王福华)