三点法传感器误差分析及一种改良方法

肖红光，肖曙红，邓志豪

(广东工业大学 机电工程学院，广州 510006)



三点法传感器误差分析及一种改良方法

肖红光，肖曙红，邓志豪

(广东工业大学 机电工程学院，广州 510006)

为了减小传感器定位对测量结果的影响和传感器拆装麻烦以及传感器多问题，提出了一种改进的三点法。该方法通过简化模型，计算出传感器的定位误差、倾斜度误差、错位误差的测量误差值，比较传感器不同方向的误差计算值，结合高精度旋转刻度盘和光栅尺，对测量结构进行改善。实验结果表明，该方法能够正确分离工件的形状误差和回转误差，测量误差能够达到±0.05μm，测量重复性好，能够减小工件的检测成本和安装时间。

误差分离；三点法；圆度误差；单传感器；旋转刻度盘

0 引言

中国是制造业大国，先进制造技术和精密加工是推动国家经济发展和提高竞争力的关键。在加工工件中，回转工件是整个机构和机器的重要部分，决定了转子的精度和机构的整体性能，故对回转类工件的精度要求也越来越高。而机床主轴作为机床的核心部件，其误差直接映射到工件上，直接影响工件的表面精度和形位公差。主轴误差有形状误差和回转误差两部分组成，故对主轴误差分离技术众多，各有侧重。

国内外误差分离方法众多。其中，经典的有Donaldon反转法，适用于准确度不是很高的转台式圆度仪[1]。Grejda用高精度转盘改进了Donaldon反转法，提高误差分离的精度，并达到纳米级精度，所使用度转盘精度高，成本昂贵。多极点法和多步法都成功实现对误差的分离，达到了纳米级的精度[2-3]。国内学者也在这方面进行了大量研究，上海大学的徐可伟，朱训生对几种常用的圆度误差分离方法进行了分析和比较，分析了几种方法应用场所和优缺点[4]。张宇华，王晓琳分析了误差分离方法的原理，测量误差的传播规律，并提出了4点法和n点法[5]。还有学者提出数理统计误差分离方法和垂直两点法[6-8]，此外还有很多学者对误差来源和误差改良进行了研究[9-11]。然而大多数学者都是对误差分离方法和测量原理进行理论研究，目前并没有学者对实际检测过程中传感器安装的误差对测量结果的影响进行研究，而且随着设备精度的提高，传感器的安装精度的确会影响测量结果。本文研究了误差分离方法中经典的三点法，对三点法主要误差分离来源——传感器定位误差的几种误差来源(传感器定位误差，传感器倾斜度误差，传感器错位误差)进行定量计算和分析，并针对传感器误差来源，提出一种三点法改良的用单一传感器结合旋转刻盘的方法，并结合实验验证该方法的正确性。

1 三点法简介

三点法是由日本学者青木保雄和大园成夫在1996年提出来，如图1所示、三点法有三个不同位置的传感器测量工件的外围信号S1(θ)、S2(θ)、S3(θ)。其中S1(θ)是水平放置的传感器，S2(θ)，S3(θ)与S1(θ)的夹角分别为α、β。测量时，传感器固定不动，工件转动。把每组测量的数据用圆度误差A(θ)和X(θ)、Y(θ)回转误差表示，有：

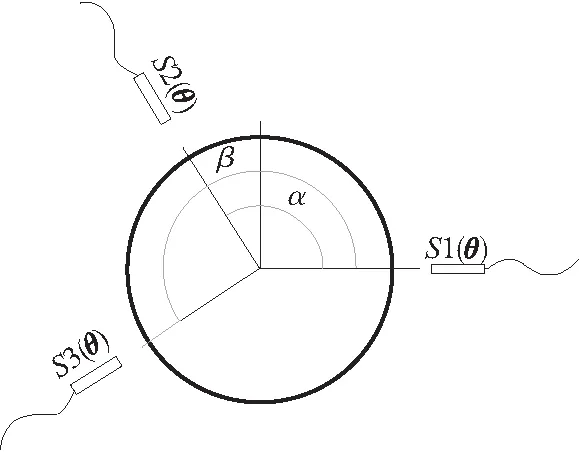
图1 三点法示意图

(1)

S2(θ)=A(θ-α)+X(θ)cosα+Y(θ)sinα

(2)

S2(θ)=A(θ-β)+X(θ)cosβ+Y(θ)sinβ

(3)

工件的外围信号S(θ)可有三个传感器加权表示：

S(θ)=S1(θ)+aS2(θ)+bS3(θ)

(4)

S(θ)=A(θ)+aA(θ-β)+bA(θ-α)+X(θ)(1+
acosα+cosβ)+bY(θ)(asinα+bsinβ)

(5)

要实现误差分离必须提出信号里面的回转误差分量故需：

令：

1+acosα+bcosβ=0

(6)

asinα+bsinβ=0

(7)

可求：

(8)

(9)

再对式(5)进行傅里叶转化有：

S(K)=A(K)×W(K)

(10)

其中，W(k)为权函数可表示为：

W(K)=1+ae-jkα+be-jkβ

(11)

故

(12)

再进行反傅里叶转换即可分离出圆度误差及：

(13)

同样可以用矩阵的方法对误差进行分离，在此不多介绍。

求出工件的圆度误差之后通过式(1)和(2)即可求出工件的回转误差。

回转误差X轴方向分量为：

X(θ)=S1(θ)-A(θ)

(14)

回转误差Y轴方向分量为：

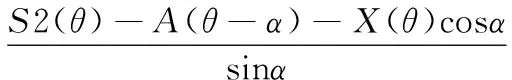
(15)

2 三点法来源分析

三点法安装简单能实现在线测量，测量不确定度能达到纳米精度，是最经典的几种误差分离方法之一。下面对三点法的误差来源进行完整的，定量的分析。从数学上定量研究了传感器定位误差、倾斜度误差和错位误差对测量精度的影响[12]。

2.1 传感器定位误差

三点法测量有两种方式，第一种用三个传感器，这样三个不同的传感器性能之间的差异对测量产生影响，第二种方式是用一个传感器，测量一个之后把传感器旋转α测量第二，再进行第三次测量。第二能够避免不同传感器之间性能之间的差异，但是测量步骤更为麻烦。在研究测量传感器定位时，不管第一种方法还是第二种方法，我们假设两次传感器对于理想状态的误差角度都为φ,如图2,有：

图2 传感器定位误差

(16)

S2′(θ)=A(θ-α-φ)+X(θ)cos(α+φ)+Y(θ)sin(α+φ)

(17)

S3′(θ)=A(θ-β-φ)+X(θ)cos(β+φ)+Y(θ)sin(β+φ)

(18)

S′(θ)=A(θ)+aA(θ-β-φ)+bA(θ-α-φ)+
X(θ)(1+acos(α+φ)+cos(β+φ))+bY(θ)
(asin(α+φ)+bsin(β+φ))

(19)

误差e(θ)为:

e(θ)=S′(θ)-S(θ)≈X(θ)(1+acos(α+φ)+bcos

(β+φ))+Y(θ)(asin(α+φ)+bsin(β+φ))=

X(θ)(1+acosαcosφ-asinαsinφ+bcosβcosφ-bsinβsinφ)+

Y(θ)(asinαcosφ+acosαsinφ)+bsinβcosφ+bcosβsinφ=

X(θ)(1-cosφ)-sinφY(θ)=X(θ)(1-(1-

(20)

2.2 传感器倾斜度误差

由于传感器缺乏夹具和索引硬件，传感器的旋转轴会与转子回转平面产生一定的倾斜角，设倾斜角为φ，如图3所示。因此传感器的测量信号包含转子的径向误差和轴向误差。具体为：

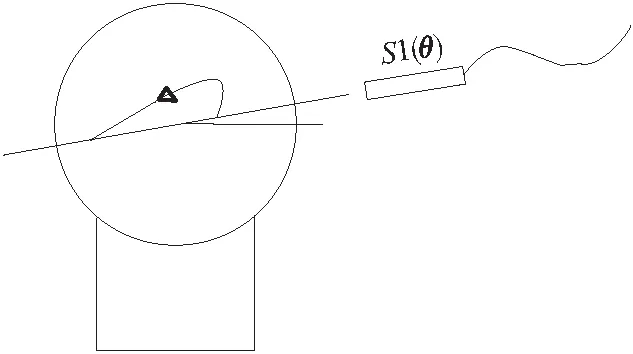
图3 传感器倾斜度误差

(21)

S2′(θ)=A(θ-α,φcosα)+X(θ)cosαcosφ+
Y(θ)sinαcosφ+Z(θ)cosαsinφ

(22)

S3′(θ)=A(θ-β,φcosβ)+X(θ)cosβcosφ+
Y(θ)sinβcosφ+Z(θ)cosβsinφ

(23)

可得:

S′(θ)=A(θ、φ)+A(θ-β,φcosβ)+A(θ-α,φcosα)+X(θ)cosφ(1+acosα+bcosβ)+Y(θ)cosφ(asinα+bsinβ)+

Z(θ)sinφ(1+acosα+bcosβ)

(24)

而在三点法中在取合适的a、b时，径向和轴向的误差都会被消除有：

S′(θ)=A(θ、φ)+aA(θ-β,φcosβ)+bA(θ-α,φcosα)

(25)

当φ特别小的时候，圆度误差A(θ)基本不受影响，对回转误差由式(26)可知:

X(θ)=S1(θ)-A(θ)=A(θ、φ)+-A(θ)≈
X(θ)cosφ+Z(θ)sinφ

(26)

e(θ)≈Z(θ)sinφ≈φZ(θ)

(27)

2.3 传感器错位误差

在理想安装情况下，传感器是垂直于旋转轴，由于存在安装误差，传感器定位如图所示。假设三个传感器都与回转轴所垂直的平面的夹角为φ。如图4所示,三个传感器所对应的信号如下：

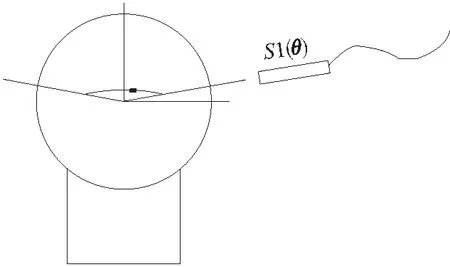
图4 传感器错位误差

(29)

S2′(θ)=A(θ-α,φ)+X(θ)cosαcosφ+
Y(θ)sinαcosφ+Z(θ)sinφ

(30)

S3′(θ)=A(θ-β,φ)+X(θ)cosβcosφ+
Y(θ)sinβcosφ+Z(θ)sinφ

(31)

可得:

S′(θ)=A(θ、φ)+aA(θ-β,φ)+bA(θ-α,φ)+
X(θ)cosφ(1+acosα+bcosβ)+Y(θ)cosφ(asinα+
bsinβ)+Z(θ)sinφ(1+a+b)

(32)

对a、b取任意值都不消除掉，取a=b=0时有：

e(θ)=Z(θ)sinφ+X(θ)(cosφ-1)≈φZ(θ)+X(θ).

(33)

2.4 三点法误差来源总结

如表1所示，对三点法的误差来源进行了分析，除去采集卡，温度等其他因素的影响，定量分析了传感器各类误差对测量误差的影响。也可从表得出，要提高的三点法的测量精度和准确性，必须提高传感器的定位精度。

表1 三点法误差来源表

3 一种三点法(多点法)改良措施

3.1 Grejda 反转法

Grejda反转法是Grejda在Donaldon反转法的基础上做出极大的改善。如图5所示，Donaldon反转法是两次测量过程中，工件和主轴固定不动，传感器旋转180°，而Grejda反转法是结合一个高精度转盘，将主轴和工件固定在这个转盘上，两次测量时，传感器固定不动，将固定在一起的旋转刻度盘、主轴旋转180°。Grejda反转法极大程度上弥补了Donaldon反转法两次测量过程中传感器安装麻烦，定位精度不高的问题，很显然旋转刻度盘的精度很明显高于传感器手动安装的精度。

(a)Donaldon反转法

(b) Grejda反转法图5 反转法

3.2 三点法的一种改良措施

相对于反转法来说，三点法的主要的优点在于工件不动，缺点在于传感器多，成本高，对于测量角度α，β安装要求高，而且每个传感器敏感度等性能不一也会影响测量精度。然而通过结合三点法和Grejda反转法中旋转刻度盘的想法的优势，就能很好克服这个问题。

具体原理如图6所示，整个电机转子固定在一个有精密刻度的旋转刻度盘上，主轴上方依次是光栅尺(用来触发采集)，工件和标注球，传感器固定不动。通过摇动手柄控制电机转子在刻度盘的转动一定角度，来实现α，β(或者更多位置)的数据采集(采集的有效性已经在Grejda反转法得到验证)[14]。该方法相对于手动安装三个传感器更加有效，精度也更高。这样做能达到的效果是，用一个传感器和高精度旋转刻度盘取代三个传感器。而且，能够在不重新安装的条件下实现多点数据采集和多角度数据采集。

平台设备主要有，旋转台设有的旋转编码器(海德时代)触发16位数据采集卡采样(NI,PXI-6123)在均匀的角增量进行数据采集，从而消除主轴转速波动的影响。传感器采用雄狮的高精度涡流传感器(Lion Precision C23-C),灵敏度为-2.042v/μm，确保测量数据精度。

在具体测量时，第一次测量(注意三次测量索引盘和定子之间的位置，箭头所指位置的变化)，如图6b，在起始位置对转子进行测量后，将转盘顺时针转动α角，旋转到如图6c位置所示，进行第二次测量；再将转子旋转β进行第三次测量，旋转到图6d所示。

(a)结构简图

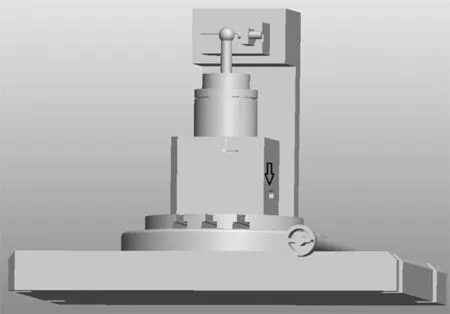
(b)第一次测量

(c)第二次测量

(d) 第三次测量图6 测量装置图

4 实验

4.1 实验仪器

Lion Precison C23-C高精度传感器，高精度旋转刻度盘，NI16位数据采集卡，触发采集的旋转编码器，高精度车削主轴。其实物图如图7所示。

图7 测试平台

4.2 测量方法的有效性

为了检验新测量方法的有效性，在确定的α，β情况下，进行多次测量，将工件分离出来的形状误差与圆度仪测量的圆度误差进行比较，并进行多次测量，测试结果如图8和表2所示。

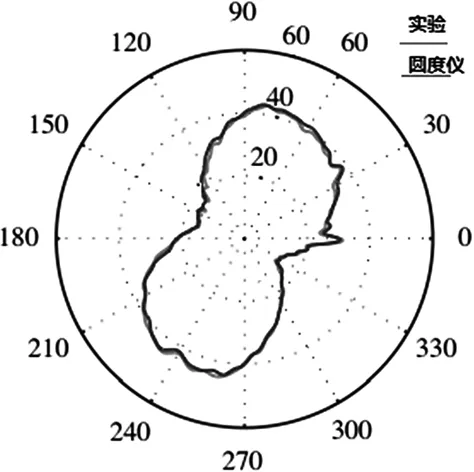
图8 圆度误差图

表2 测量数据表

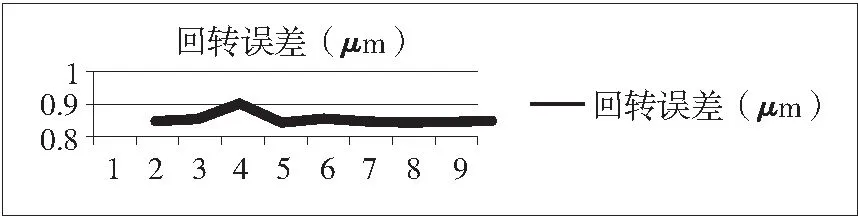
(a) 回转误差测量折线图

(b) 形状误差测量折线图图9 误差折线图

从图9可以看出实验测量图像和圆度仪测量图像基本吻合，测量结果和和圆度仪误差在±0.04um说明测量方法有效，从9次实验的测量回转误差和形状误差的折线图可以看出，测量波动比较小，测量重复性好其中9次测量的会装误差的标准差S1=0.00376,形状误差的标准差S2=0.0194。验证了实验方法的正确性。

4.3 旋转刻度盘精度的影响

本次实验主要研究旋转刻度盘的测量精度对测量结果的影响，测量三次，分别用旋转刻度盘的测量误差为0′，2′，20′时的测量数据分析和研究刻度盘的误差对测量精度的影响。测量结果如图10所示。

图10 不同旋转刻度盘测量结果图

不同的旋转刻度盘测量结果结果如表3所示。

表3 实验数据表

从上述实验来看，测量精度对旋转刻度盘的测量精度的敏感度还是比较低的，三次测量图像曲线基本能够重合。当然为了得到比较高的测量精度，旋转刻度盘的精度还是越高越好。

5 结论

文章研究了误差分离方法中经典的三点法，对三点法主要误差分离来源——传感器定位误差的几种误差来源(传感器定位误差，传感器倾斜度误差，传感器错位误差)进行定量计算和分析，并针对传感器误差来源，提出一种三点法改良的用单一传感器结合旋转刻盘的方法，该方法存在传感器只有一个，节约成本和能在不重新安装传感器的条件下，实现任意α，β的测量等优点。实验结果表明，该方法的能够准确实现误差分离，测量精度达到±0.05μm，测量重复性好，并对旋转刻度盘的精度要求不是特别高。能够再实际生产中，对工件误差进行分离，并降低成本的作用。

[1] Donaldson RR.A simple method for separating the spindle error from test ball roundness error[J].CIRP Annals 1972,21(1):125-131.

[2] Whitehouse DJ.Some theoretical aspects of the spindle error separation technology[J].Journal of Physics E 1976,9:531-537.[3] S Cappa,D Reynaerts, F Al-Bender.A sub-nanometre spindle error motion separation technique[J]. Precision Engineering，2015(7):002.

[4] 徐可伟，朱训生,陈正昕.几种常用圆度误差分离方法的分析及比较[J].计量技术,2000(8):26-28.

[5] 张宇华，王晓琳,张国雄,等.多点法圆度及轴系误差分离方法的若干问题[J].北京理工大学学报，1999,19(3):309-313.

[6] 夏欢，陶继忠.空气静压轴承主轴回转精度测试研究[J].轴承，2013(7):56-58.

[7] 陆峰，沈鸿波,张啸飞,等.基于垂直两点法的电主轴回转误差精度分析[J].组合机床与自动化加工技术，2014(11):14-18.

[8] 雷贤卿，李言,周彦伟,等.3点法圆度误差分离技术的新算法[J].兵工学报，2007,28(1):73-77.

[9] 熊万里，候志泉,吕浪.液体静压主轴回转误差的形成机理研究[J].机械工程学报，2014,50(7):112-119.

[10] 靳岚,燕昭阳，谢黎明，等.高速电主轴回转误差动态测试与分析[J].制造技术与机床，2012(4)：93-95.

[11] 姚俊，王平，主轴回转精度测量方法[J].制造技术与机床，2011(2)：176-180.

[12] K Prashanth Anandan.A multi-orientation error separation technique for spindle metrology of miniature ultra-high-speed spindles[J].Precision Engineering ,2015，7.

[13] Grejda RD,Maesh ER,Vallance R.Techniquces for calibrating spindles with nanonerer error motion[J].Precion Engineering 2005,29:113-136.

(编辑 李秀敏)

Sensor Error Analysis and an Improved Method in the Multiprobe Technique

XIAO Hong-guang,XIAO Shu-hong,DENG Zhi-hao

(School of Mechanical Engineering, Guangdong University of Technology, Guangzhou 510006,China)

In order to reduce the influence of sensor location on the measurement results and the trouble of sensor assembly and disassembly, an improved multiprobe technique is proposed. This method simplifies the model, calculate the measurement error of location error and sensor error, tilt error, calculation error comparing sensor in different directions, combined with high precision rotary dial and grating, the improvement of measurement structure. The experimental results show that this method can correctly separate the shape error and rotation error of the artifact, the measurement accuracy can reach 0.04μm, the measurement repeatability is good, and the cost and installation time can be reduced.

error separation; multiprobe technique; roundness error; single sensor; rotary dial

1001-2265(2017)06-0054-05

10.13462/j.cnki.mmtamt.2017.06.014

2016-08-30；

2016-10-09

肖红光(1991—)，男，湖北黄冈人，广东工业大学硕士研究生，研究方向为高速轴误差测量和分离研究，(E-mail)670186230@qq.com。

TH161;TG506

A