地月系L2平动点轨道长期维持过程研究

梁伟光，周文艳，周建亮，杨维廉

（1. 北京航天飞行控制中心，北京 100094；2. 北京空间飞行器总体设计部，北京 100094）

地月系L2平动点轨道长期维持过程研究

梁伟光1,2*，周文艳2，周建亮1，杨维廉2

（1. 北京航天飞行控制中心，北京 100094；2. 北京空间飞行器总体设计部，北京 100094）

针对地月系L2平动点附近两种常用轨道——拟halo轨道和Lissajous轨道，研究了轨道长期维持过程。采用穿越xz平面单圈控制的轨道维持策略，控制量通过单步预测法进行寻优。在全摄动动力学模型下对拟halo轨道和Lissajous轨道受控维持下的一年飞行过程分别进行了仿真和比较，结果显示Lissajous轨道的维持控制代价优于拟halo轨道，从轨道拓扑构型保持方面对该结果进行解释，并设计对比实验加以验证。研究结论对地月系L2平动点轨道选择、维持控制策略设计、长期飞行效果分析等方面具有工程参考意义。

地月系L2平动点；长期维持；拟halo轨道；Lissajous轨道

0 引 言

地月系L2平动点在深空探测中具有重要的意义，可以作为支持月球背面着陆探测的中继卫星长期运行轨道，也可以为定点探测、星际转移、深空星座布局等提供轨道动力支持。由于L2平动点是三体问题中的不稳定平动点，位于L2平动点附近的轨道往往对轨道初值十分敏感，而且地月系L2平动点附近还存在多种摄动因素，因此航天器在地月系L2平动点附近飞行时，容易因轨道的不稳定发散而飞离L2平动点，如果要保持长期稳定飞行，则需实施必要的平动点轨道维持控制。

迄今为止，人类共实现了两次地月系L2平动点飞行任务，分别为美国的ARTEMIS任务和我国的探月工程三期再入返回飞行试验器服务舱拓展试验任务。两次任务都实现了沿Lissajous轨道绕飞地月系L2平动点多圈，且均采用了过xz平面的单圈轨道维持技术。然而这两次任务飞行时间均较短（分别为129天[1]和38天），Lissajous轨道均未实现全空间包络覆盖。目前关于地月系L2平动点的轨道维持研究多集中于理想的三体问题模型下进行，对真实动力学环境下轨道维持的研究仅针对ARTEMIS任务飞行周期内的过程展开[2-4]。

本文对地月系L2平动点附近的拟halo轨道和Lissajous轨道进行了长期飞行方面的研究，设计了单步预测的单圈控制策略，在考虑三体引力摄动的动力学模型下对两种轨道进行了维持控制下长期飞行过程的仿真，对于呈现出的Lissajous轨道维持控制代价较小的现象，从拓扑构型方面进行了分析，并设计比对实验加以验证。研究结果对地月系L2平动点轨道设计具有工程参考意义。

1 基础理论

1.1 圆型限制性三体问题

对于地球–月球–航天器或太阳–地球–航天器这类有两个大天体和一个航天器组成的系统，忽略航天器对天体运动的影响，称为限制性三体问题。如果该问题中两个大天体绕共同质心作圆周运动，称为圆型限制性三体问题[5]。

会合坐标系（又称质心旋转坐标系）[5-6]是研究三体问题时普遍采用的坐标系。会合坐标系O-xyz的定义为：坐标系随两个主天体一起绕质心O旋转，xy坐标平面为两个主天体相对运动的平面，x轴方向由大天体指小天体，y轴方向为小天体绕质心旋转的切线方向。

根据牛顿万有引力定律，航天器在两个主天体的引力作用下的运动方程为

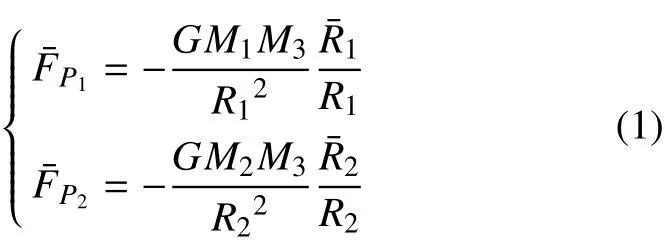
其中，G为万有引力常数。

为了分析问题和计算上的方便，对式（1）中各物理量进行无量纲化和量级归一化处理，可以得到会合坐标系中的圆型限制性三体问题动力学模型如下

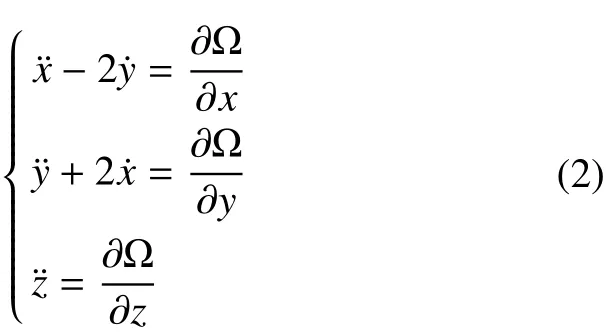
其中，Ω为等效势能函数

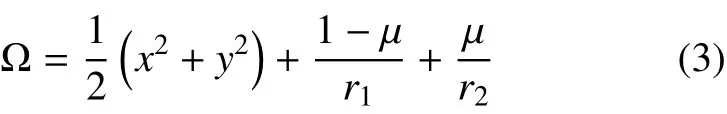
μ为小天体的质量占比

1.2 L2平动点轨道

三体问题基本方程（2）存在5个特解，对应的空间中的位置称为平动点，由于这5个特解最终由拉格朗日发现，因此平动点又被称为拉格朗日点，用L1～L5表示。其中，L2平动点位于大天体至小天体的质心连线延长线上，属于共线平动点，是三体问题中的鞍型不稳定平衡点，航天器在L2平动点附近飞行时经过小扰动即会呈近似指数型远离L2平动点。

在L2平动点附近存在多种类型的周期和拟周期轨道，其中以下三类轨道在研究和应用方面较为广泛[7]：

1）halo轨道。当会合坐标系下轨道平面（xy平面）振动频率与垂直（z向）振动频率相等时，第三体环绕平动点的轨道呈单圈闭合形式，称为halo轨道，又称晕轨道。halo轨道是周期轨道。由于实际情况很难满足“平面振动频率与垂直振动频率相等”，因此halo轨道通常仅作为理论轨道加以分析。

2）Lissajous轨道。当会合坐标系下轨道平面振动频率与垂直振动频率不相等时，第三体环绕平动点的轨道在会合坐标系下呈Lissajous曲线的形式，称为Lissajous轨道。平动点环绕轨道中Lissajous轨道占多数。

3）拟halo轨道。拟halo轨道为一类特殊形式的Lissajous轨道，这类轨道在halo轨道附近，其偏离halo轨道面的振动幅值较小。拟halo轨道是一种拟周期轨道，即没有严格的周期性，但在特定的偏差允许范围内，表现出近似的周期性。

现实三体系统由于受到多种摄动影响，不存在严格周期性的理想halo轨道，但是halo轨道所具有的单圈周期性、轨道近似共面、解析近似形式简单、动力学特性明显等良好特征，使得寻找与halo轨道近似的拟halo轨道往往成为平动点任务的现实需求。

2 地月系L2平动点轨道维持

本文针对航天器在地月系L2平动点附近长期飞行的情况，对地月L2平动点的拟halo轨道和Lissajous轨道长期位置保持过程进行了设计与仿真分析。

2.1 轨道维持方法

式（2）中的等效势能Ω是三体问题下轨道能量的体现，即无动力飞行过程中具有相同的Ω。轨道控制过程实质上是通过动力推进改变Ω。因此，在轨道飞行过程中的任意位置变轨，只需调整Ω相同，便会取得动力学特性相一致的平动点轨道。

基于等效势能调整的概念，穿越会合坐标系xz平面修正具有调整参数较少的特点[8]。因此，在对平动点绕飞轨道实施位置保持控制时可采用以下控制策略：

1）调整x和z向速度接近于零。

2）调整y向速度使绕飞持续。

由于针对halo轨道的保持控制通常选取穿越xz平面附近进行，而以Lissajous轨道为代表的拟周期轨道未有具体的控制位置限定。参考国内外已实施的平动点任务的轨道维持策略[2,9]，同时为便于研究中的统一比较和分析，本课题将Lissajous轨道的控制时刻也选为穿越xz平面。

尽管控制时机以每半圈穿越xz平面为单位，但在数值仿真和实际任务中，保持连续绕飞一圈以上的平动点轨道对初值的要求并不苛刻。以地月系和日地系为例，位置测量精度为1 km，控制速度量标定精度为1%时，即可实现绕飞平动点2圈。因此，平动点轨道位置控制可以以半圈为单位，进行每圈一控，或每两圈一控。

圆型限制性三体模型下的数值计算效果，在初值选取合适时可以实现多圈绕飞，之后的轨道保持控制的速度增量相比存在摄动时明显降低（1/10以下）。然而圆型限制性三体问题并非真实环境，且共线平动点的不稳定性对绕飞轨道控制效果影响很大。因此，我们对绕飞轨道控制过程的实现与讨论主要在更加精确的深空动力学环境下进行。

由于地月L2平动点附近的鞍型不稳定性，平动点轨道保持控制对初值和控制精度影响非常敏感，经过多次实验，我们发现，在实际工程约束下，针对平动轨道的单圈控制过程，第n圈（n≥1）的控制残差，对第n + 1圈的控制量影响较明显，而对第n + 2圈的控制量大多超出控制量阈值，即两步及多步后的预测控制量不适合。因此，可以仅选用单步预测的控制量作为指标函数，以单步预测控制量最小为目标，对每圈的控制量进行优化选择。单步预测优化控制过程如图 1所示。

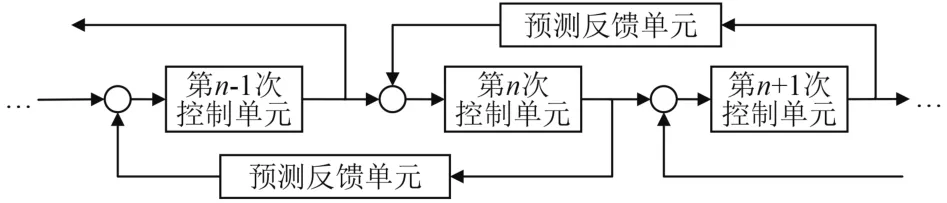
图 1 单步预测控制流程图Fig. 1 Single step prediction control flow chart

2.2 拟halo轨道长期飞行

halo轨道初值通过三阶近似解析式[10]算得，利用数值积分计算绕飞过程。在此基础上采用多数平动点绕飞任务单圈控制的策略，模拟了halo轨道单圈控制效果。选取了地月系全弧段规避月掩[11]最小halo轨道。考虑地月系中太阳引力作为重要摄动源，而地月系相对太阳的运行周期以年为单位，做了飞行1年的长期halo轨道保持控制效果的仿真，受控绕飞过程如图 2所示，控制参数如表 1所示。

图 2 长期飞行拟halo轨道Fig. 2 Long term quasi-halo orbit

通过受控拟halo轨道长期飞行的仿真效果可以看出：

1）单圈控制方法可以实现航天器沿拟halo轨道长期绕飞L2平动点。

2）在长期飞行过程中，飞行时长和速度增量均变化平稳。

3）轨道构型的发散程度不随时间增加而增加，因而可以实现长期保持。

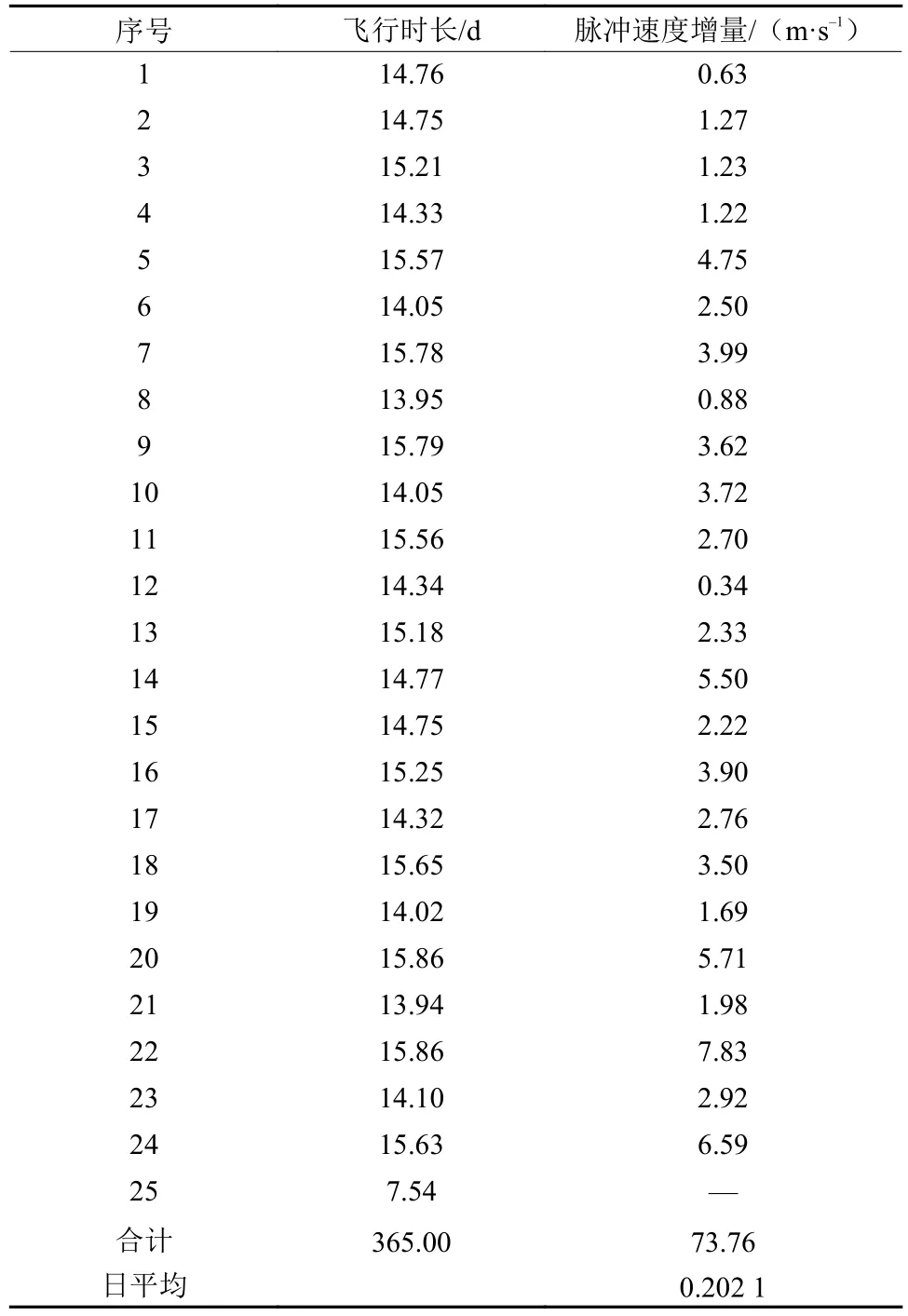
表 1 拟halo轨道保持控制参数Table 1 Quasi-halo orbit station keeping control parameters

2.3 Lissajous轨道长期飞行

选用探月工程三期再入返回飞行试验器服务舱绕飞地月系L2平动点的Lissajous轨道作为初始轨道，对受控的Lissajous轨道1年的绕飞过程进行仿真，如图 3所示，相应的控制参数如表 2所示。

图 3 长期飞行Lissajous轨道Fig. 3 Long term Lissajous orbit

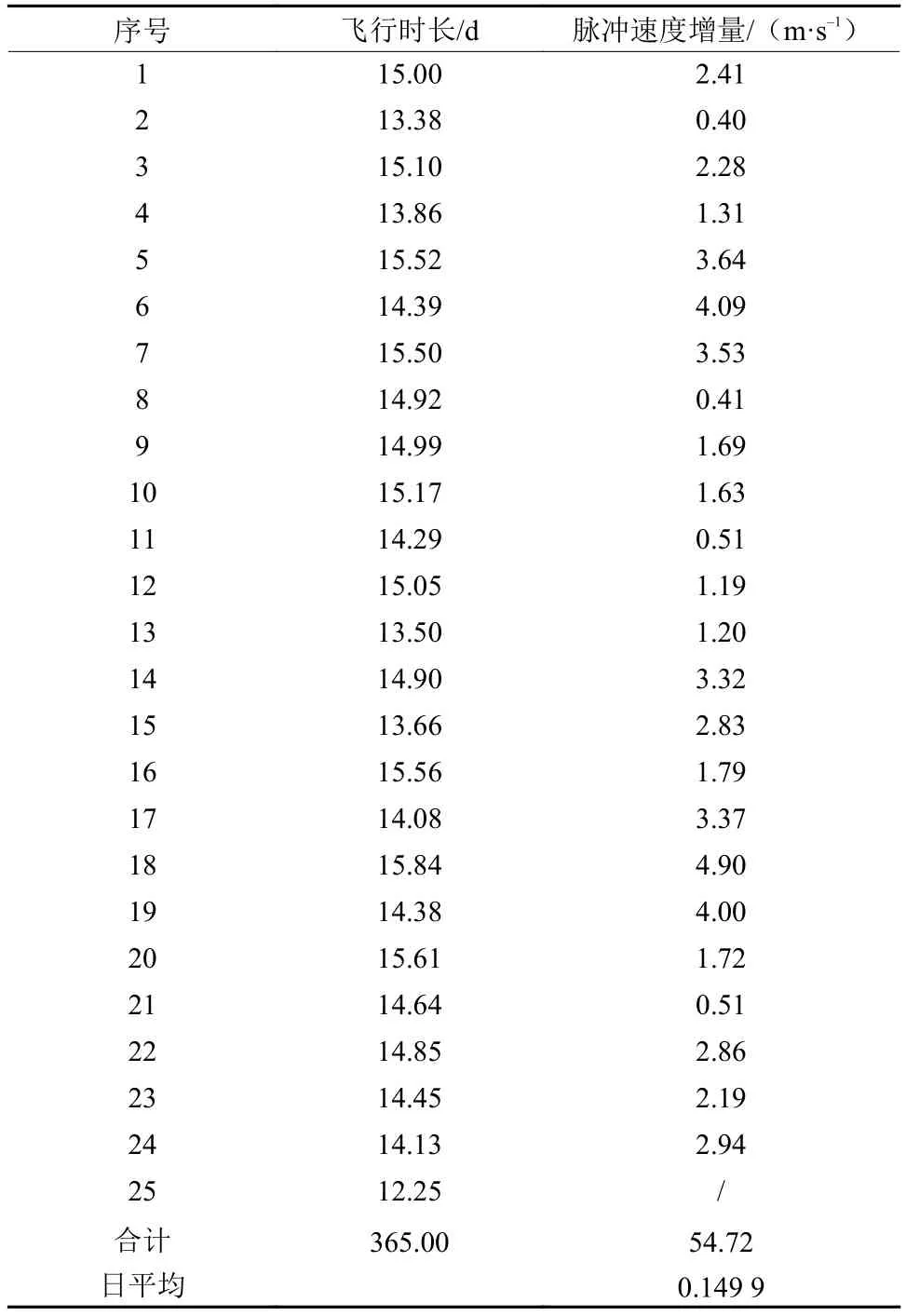
表 2 Lissajous轨道保持控制参数Table 2 Lissajous orbit station keeping control parameters

通过受控Lissajous轨道长期飞行的仿真效果可以看出：

1）穿越xz平面的单圈控制方法可以实现航天器沿Lissajous轨道长期绕飞L2平动点。

2）在长期飞行过程中，单圈飞行时长和维持控制速度增量均变化平稳。

3）Lissajous轨道拓扑构型演化程度稳定，可以实现长期保持。

2.4 维持控制代价分析

上述两种轨道（图 2～3）的构型在L2平动点附近的范围相似（图 4），从等效势能梯度矢量场[5]可知两种轨道的等效势能Ω也相近。因此，两种轨道具有可比性。

由表 1和表 2的单次维持控制效果和统计结果可以看出：Lissajous轨道的维持控制代价优于拟halo轨道。对于此差别，可以有如下解释：

1）拟halo轨道因有较为严格的拓扑构型，轨道维持时对轨道保持的精度较高。在仿真精度难以达到严格的位置保持精度时，控后轨道构型较标称轨道有所偏离，积累到后续的轨道维持控制时，需要消耗较大的控制量以将轨道调整回拟halo轨道，从而保持长期飞行。

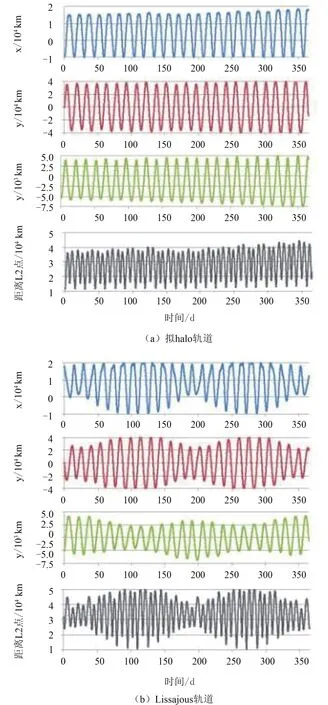
图 4 平动点轨道特征Fig. 4 Libration point orbits characteristics

2）Lissajous轨道的拓扑构型相较拟halo轨道更为宽松，仅需平面振动频率和垂直振动频率不相等即可。轨道维持控制后即使有所偏离，也位于地月系L2平动点附近，且有可能会进入其他的Lissajous轨道[12]，这种差别相对细微，在长期飞行中难以从轨道构型中体现。因此，对控制量的约束相比拟halo轨道较小（只需长期维持在L2平动点附近即可），于是可以在保证长期飞行的情况下对控制量进行更好的选优，以实现全程控制量较小。

为了验证Lissajous轨道长期飞行期间可以改变构型的情况，选用图 3相同的初轨，在飞行中期对控制量作了微调，轨道效果如图 5所示。为了显示轨道构型改变效果，3D视图选取了接近月球的视角。可以看出飞行轨道出现了两种Lissajous构型之间的过渡，且仍能保持在L2平动点附近长期飞行。于是上述关于Lissajous轨道控制量约束相对较小的分析结论得以验证。

图 5 中途调整控制量的Lissajous轨道Fig. 5 Lissajous orbtit with control value tuning halfway

3 结束语

本文研究了地月系L2平动点附近的两种平动点轨道——拟halo轨道和Lissajous轨道。通过轨道维持进行长期飞行的过程，在单圈轨道维持控制实现长期飞行的基础上，通过仿真得出了Lissajous轨道的维持控制代价优于拟halo轨道的结果，并通过轨道构型分析和对比实验进行了解释。

后续还将对其他类型的平动点轨道（如Lyapunov轨道、轴向轨道、垂直轨道等）的长期维持过程进行全面研究，并将研究引入位置速度误差情况下的长期维持效果。

[1]Sweetser T H，Broschart S B，Angelopoulos V，et al. ARTEMIS mission design [J]. Space Sci. Rev. 2011，165（1-4）：27-57.

[2]Folta D，Woodard M，Cosgrove D. Station keeping of the first Earth-Moon libration orbiters：the ARTEMIS mission [C]//AAS/AIAA Astrodynamics Specialist Conference. AAS11-515，Girdwood ，Alaska，USA：AAS，2011：1-20.

[3]Pavlak T，Howell K C. Evolution of the out-of-plane amplitude for quasi-periodic trajectories in the Earth-Moon system [J]. Acta Astronautica，2012，81（2）：456-465.

[4]Folta D C，Pavlak T A，Haapala A F，et al. Earth-Moon libration point orbit station keeping：theory，modeling，and operations [J]. Acta Astronautica，2014，94（1）：421-433.

[5]Szebehely V. Theory of orbits：the restricted problem of three bodies [M]. New York and London：Academic Press，1967.

[6]Mcinnes A. An introduction to libration point orbits [EB/OL]. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.516.7677&re p=rep1&typepdf.

[7]Rend F，Landgraf M. Sun-Earth libration point transfer options with intermediate HEO [J]. Acta Astronautica，2012，74（3）：1-19.

[8]Pavlak T，Howell K C. Strategy for long-term libration point orbit station keeping in the Earth-Moon system [C]//AAS/AIAA Astrodynamics Specialist Conference. AAS11-516，Girdwood，Alaska，USA：AAS，2011：1-18.

[9]Canalias E，Gomez G. Marcote M，et al. Assessment of mission design including utilization of libration points and weak stability boundaries [R]. ACT net（www.esa.int/act），2004.

[10]Richardson D L. Analytic construction of periodic orbits about the collinear points [J]. Celestial Mechanics，1980，22：241-253.

[11]Farquhar R W. The control and use of libration-point satellites [R]. USA：NASA Technical Report. R-346，Glddard Space Flight Center，1970.

[12]Canalias E，Cobos J，Masdemont J J. Impulsive transfers between Lissajous libration point orbits [J]. Journal of the Astronautical Sciences，2003，51（4）：361-390.

通信地址：北京市5130信箱112分箱（100094）

电话：（010）66360291

E-mail：lwgustc@163.com

Earth-Moon L2 Libation Point Orbit Long Term Station Keeping

LIANG Weiguang1,2*，ZHOU Wenyan2，ZHOU Jianliang1，YANG Weilian2
（1. Beijing Aerospace Control Center，Beijing 100094，China；2. Beijing Institute of Spacecraft System Engineering，Beijing 100094，China）

Earth-Moon L2 libration point is unstable. The necessary orbit station keeping operations are required for spacecraft in order to maintain around Earth-Moon L2 libration point for a long time. Long term station keeping operations fortwo types of orbits, quasi-Halo orbit and Lissajous orbit, are studied. Control once per cycle when crossing the xz plane is used as the control strategy. Control values are chosen by single step prediction. One year trajectories of quasi-Halo orbit and Lissajous orbit with station keeping are simulated in the real celestial mechanics model respectively. Comparison of simulation results shows that the cost of station keeping for Lissajous orbit is lower than that of the quasi-Halo orbit. This can be explained from orbit topological configuration. Corresponding contrast experiment is designed to verify the inference. Research results have engineering reference for Earth-Moon L2 libration point selection, station keeping control strategy design, long term trajectory and effect analysis.

Earth-Moon L2 libration point；long term station keeping；quasi-halo orbit；Lissajous orbit

V412.4+1，V448.232

A

2095-7777（2017）02-0166-05

10.15982/j.issn.2095-7777.2017.02.010

梁伟光（1982– ），男，工程师，主要研究方向：三体问题，平动点轨道，深空低能转移。

[责任编辑：高莎，英文审校：朱鲁青]

梁伟光，周文艳，周建亮，等. 地月系L2平动点轨道长期维持过程研究[J]. 深空探测学报，2017，4（2）：166-170.

Reference format: Liang W G，Zhou W Y，Zhou J L，et al. Earth-Moon L2 libation point orbit long term station keeping [J]. Journal of Deep Space Exploration，2017，4（2）：166-170.

2015-11-10

2015-12-08