潜在威胁小行星碰撞防御的计算与分析

姜宇，程彬，宝音贺西，李恒年

（1. 西安卫星测控中心宇航动力学国家重点实验室，西安 710043；2. 清华大学 航天航空学院，北京 100084）

潜在威胁小行星碰撞防御的计算与分析

姜宇1,2*，程彬2，宝音贺西2，李恒年1

（1. 西安卫星测控中心宇航动力学国家重点实验室，西安 710043；2. 清华大学 航天航空学院，北京 100084）

研究了采用碰撞的方式进行小行星防御的动力学问题。采用多面体模型来建立小行星的外形模型，以碎石堆模型来建立小行星的结构模型，计算了小行星受到与其密度和材质相同的球体高速碰撞过程和碰撞后的碎石分布。计算过程在考虑了小行星与碰撞球体的接触形变以及小行星内部组成碎石堆的接触形变条件下，计算了碎石堆内部的相互引力、法向接触力、切向静摩擦力、切向动摩擦力和滚动摩擦力矩。以小行星101955 Bennu（中文名贝努）为对象计算了潜在威胁小行星的碰撞防御过程的动力学行为。结果显示：采用高速碰撞的方法进行小行星防御可以有效地将小行星撞成大量碎小的石块，且该方法具有核爆的方法不可比拟的优势，即对空间环境无污染。

潜在威胁小行星；小行星防御；小行星碰撞；碰撞防御；碎石堆小行星

0 引 言

有的小行星属于潜在威胁[1-6]的小行星，这类小行星可能与地球相撞。对于已确定将要撞击地球的小行星[3]，可以采用对小行星进行变轨控制[1]、对小行星进行碰撞[4-6]或使用核武器将其引爆[7]等方式将其炸毁。Quarta和Mengali[1]研究了采用电动太阳帆进行潜在威胁小行星的交会任务，并与采用平坦的太阳帆进行潜在威胁小行星的交会进行了比较。Vardaxis等[4]研究了针对潜在威胁小行星进行碰撞的从地球至小行星的转移轨迹设计。Michel等[5]研究了采用冲击动能技术偏转双小行星系统65803 Didymos过程中的动力学参数，该研究的背景是小行星碰撞与偏转评估（Asteroid Impact & Deflection Assessment，AIDA）任务[5-6]，AIDA是第一个针对双小行星系统表面及内部进行观测与探索的任务。Lomov等[7]研究了采用核爆的方式摧毁小行星来防止潜在威胁小行星碰撞地球，研究表明该方式可以提供足够的能量来摧毁小行星内部结构的完整性。此外，他们发现无孔结构的固体岩石状小行星在受到核爆时的损伤程度比含大量孔隙结构的小行星在受到核爆后损伤程度大，因为无孔结构无法像多孔介质那样衰减核爆形成的冲击波，尽管多孔介质小行星的结构强度不如前者。Koenig和Chyba[8]从动量定理出发研究了采用动能冲击来偏转小行星轨道的方法，考虑了小行星的质量和相对速度。

本文以潜在威胁的小行星101955 Bennu（中文名贝努）[2,9-10]为例，研究了采用碰撞来摧毁小行星的方法并计算了碰撞过程的相关参数。美国于2016年9月8日发射的OSIRIS-REx任务探测器预计于2018年抵达小行星101955 Bennu，采样后将于2023年返回地球[2]。2013年俄罗斯车里雅宾斯克州陨石事件的陨石在进入大气层以前的直径约为15 m，造成了超过700人受伤和大量建筑物受损[11-12]，而小行星101955 Bennu的直径约为492 m[2]，如果撞击地球，灾难将是毁灭性的。

本文研究通过高速碰撞将小行星撞击成大量碎片。对于将要撞击地球的小行星来说，在其撞击地球以前，人类将该小行星撞击成大量碎片，进入大气层的部分碎片会烧毁，不至于造成严重灾难。研究表明，尺度在小行星五分之一大小量级的球体高速碰撞小行星可以把小行星完全撞碎。与采用核爆的方式撞碎小行星相比，这种方法无辐射污染，在保护环境方面具有明显的优势。

1 小行星101955 Bennu的形状与物理特征

使用多面体模型来建立小行星的外形与引力场模型，小行星101955 Bennu的引力势[13]

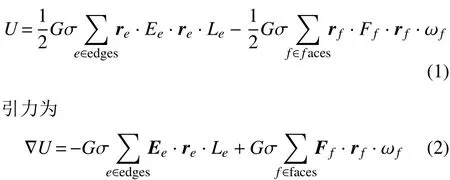
其中：G = 6.67 × 10–11m3kg–1s–2表示牛顿引力常数，σ表示小行星101955 Bennu的体密度，re和rf分别为小行星本体固连坐标系中表示的从场点分别到边e和面f的向量，Ee和Ff分别为多面体模型的边和面的参数，Le为多面体模型中场点和边的积分因子，ωf为相对多面体模型中场点的带符号的角度。小行星101955 Bennu[14-15]的自旋周期为4.288 h，平均直径为492 ± 20 m，体密度为0.95 g/cm3。

图 1给出了小行星101955 Bennu的有效势[9-10,14-16]的整体结构情况和在各平面的投影结构。图 2给出了小行星101955 Bennu不规则几何形状及平衡点的位置关系以及平衡点和有效势能分布的位置关系。计算过程采用的小行星101955 Bennu物理模型含有1 348个顶点和2 692个面。由图 1（b）和图 1（c）可见，小行星101955 Bennu的有效势在xy平面的分布和在yz平面及zx平面的分布完全不同，有效势在yz平面及zx平面的结构基本类似。图 1（a）给出了小行星101955 Bennu的有效势在xy平面的大小数值，由此可见，小行星101955 Bennu的xy平面有效势存在临界点。对比图 1（a）和图 2（b）、图 2（e）可知该小行星有效势和平衡点的位置关系。小行星101955 Bennu共有9个平衡点，其中1个位于小行星体内，8个位于小行星体外。从稳定性和拓扑类型的角度来看，位于小行星体内的平衡点是稳定的，另外位于小行星体外的8个平衡点都是不稳定的。由图 2（c）和图 2（d）可见，小行星101955 Bennu的平衡点并未落在一个平面内。事实上，这些平衡点都是非赤道面的平衡点，都落在小行星101955 Bennu自旋的赤道面以外。

由图 1和图 2可见，小行星101955 Bennu的形状与物理特征较为复杂，外部有8个相对平衡点，也就是不规则外形与引力分布引起的有效势能临界点有8个。临界点偏离赤道面，说明该小行星南北并非对称。因此，在研究小行星101955 Bennu作为潜在威胁的小行星进行碰撞时，不能简单地将该小行星作为圆球或椭球来考虑，否则将不能真实地模拟该小行星的不规则几何外形及其引起的引力场环境。此外，虽然101955 Bennu的物理模型与外形数据是通过多面体模型给出的，包含数千个顶点和面，但多面体模型作为一个整体，仅在计算小行星的几何外形和引力场乃至计算其引力场中的动力学行为方面存在诸多优势，而无法计算小行星受到碰撞发生断裂或碎石堆小行星解体成大量碎石的过程。因此我们需要寻找一种方法，既能良好地保留多面体模型关于小行星不规则外形的模拟优点，能较为精确地还原小行星的真实外形，又能良好地模拟碎石堆小行星的内部结构。

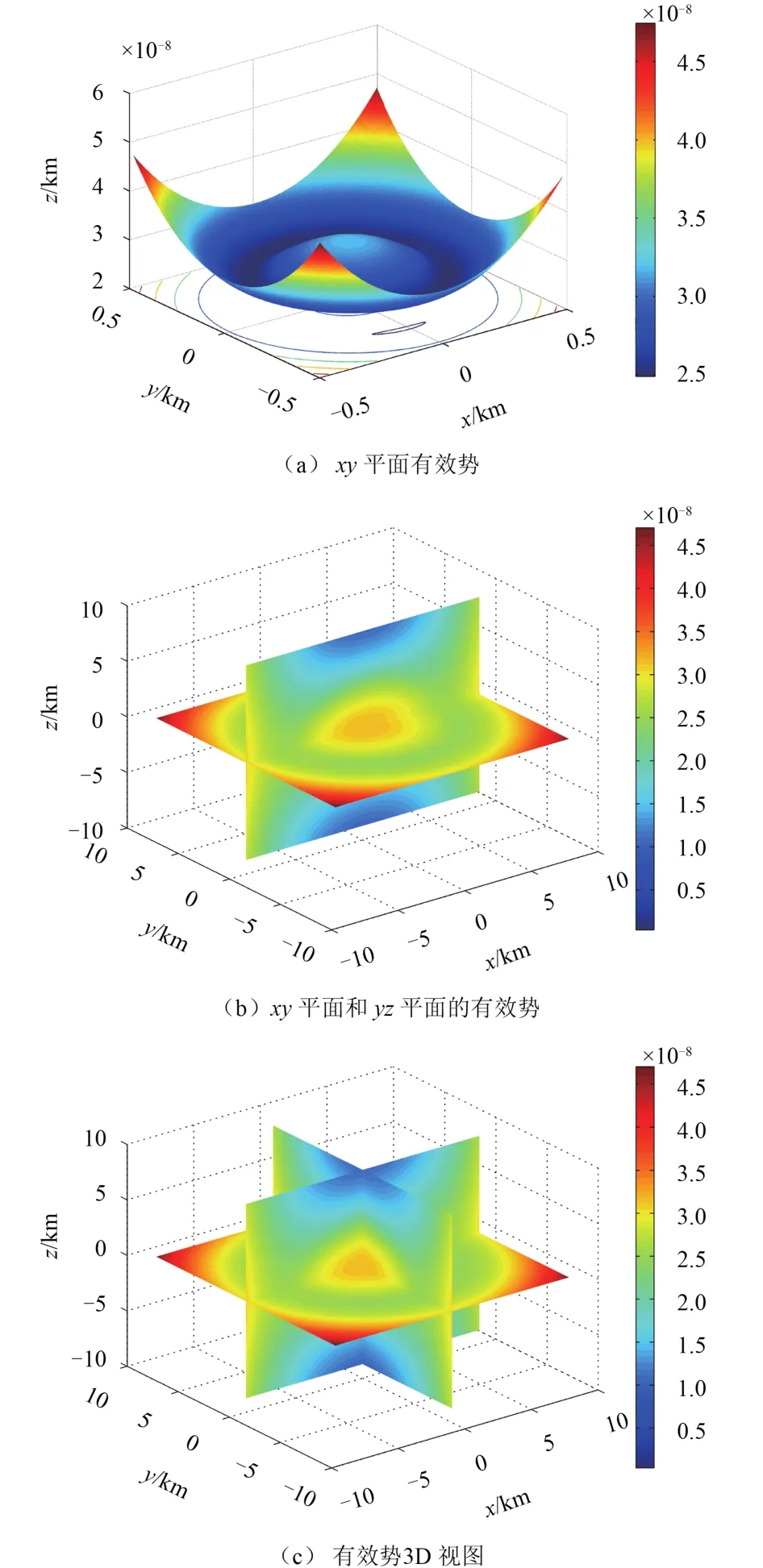
图 1 小行星101955 Bennu的有效势Fig. 1 Effective potential of the asteroid 101955 Bennu

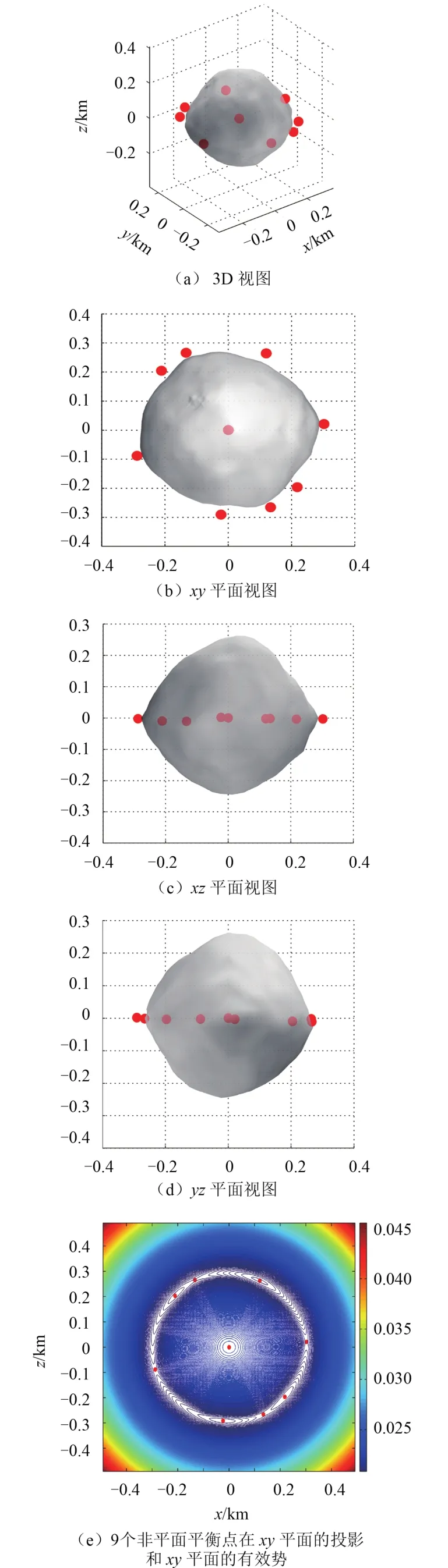
图 2 小行星101955 Bennu的形状及平衡点Fig. 2 The shape and equilibrium points of the asteroid 101955 Bennu

2 小行星101955 Bennu碰撞的数值计算

根据已有的小行星近距离探测及热红外成像数据，我们发现大部分直径在100 m～100 km之间的小行星（包括101955 Bennu）是由直径几毫米至几十米的碎石颗粒在引力作用下聚合形成的，即“碎石堆”结构。这些颗粒之间具有接触力和引力的作用，相邻颗粒之间存在碰撞、摩擦和滚动。在力的作用下，相邻颗粒之间并非刚性接触，而是存在着接触形变。采用软球离散元耦合引力N体模型可以很好地模拟这样的力学行为[17]。这里我们采用软球离散元方法来建立小行星的碎石堆模型。通过足够多的球来填充小行星的通过多面体模型数据建立的几何外形的内部，从而得到采用碎石堆模型表示的小行星的内部结构和外形。在小行星碎石堆模型中，相邻碎石颗粒之间考虑法向的弹性力和阻尼力，而在切向则考虑弹性力、阻尼力、滑动力、滚动力及合力矩。

第p个小球受到的合力Fp与合力矩Mp采用下式计算[18]

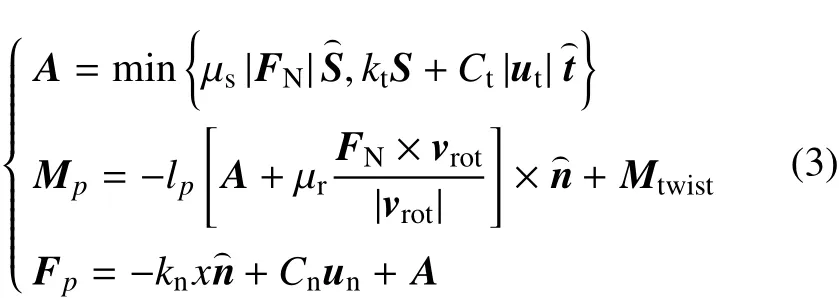
其中：kn为法向接触刚度；kt为切向接触刚度；Cn为法向阻尼系数；CT为切向阻尼系数；FN为法向接触力；S为相对于平衡接触点的切向位移；为S的单位矢量；为相邻颗粒间的法向单位矢量；为切向单位矢量；μs为静摩擦系数；μr为滚动摩擦系数；un为总的相对速度的法向分量；ut为总的相对速度的切向分量；A为中间变量；vrot为滚动摩擦系数计算的中间过程量；x为相邻颗粒之间的重叠量。

法向与切向接触刚度需保证碰撞过程中颗粒最大重叠量不超过最小颗粒半径的1%，即xmax约等于1%Rmin，一般通过下式确定

其中：m为颗粒质量，vmax为颗粒系统最大碰撞速度，Rmin为最小颗粒半径，εn为法向弹性恢复系数，μ为特征碰撞对约化质量。

以碎石堆模型来模拟小行星101955 Bennu的外形与内部结构，采用4 875个颗粒来填充多面体模型。设正向弹性恢复系数为0.5，滑动摩擦系数为0.5，滚动摩擦系数为0.55。计算的时间步长为微秒，即1 μs = 1.0 × 10–6s。计算得到正向刚度系数为2.094 395 × 1011，正向阻尼系数为4.512 453 × 108，切向刚度系数为5.983 986 × 1010，切向阻尼系数为7.931 700 × 107。

图 3给出了小行星101955 Bennu受到碰撞过程的数值计算结果。为了便于观察，采用碎石颗粒的颜色来表示小行星表面及内部碎石颗粒的相对速度。

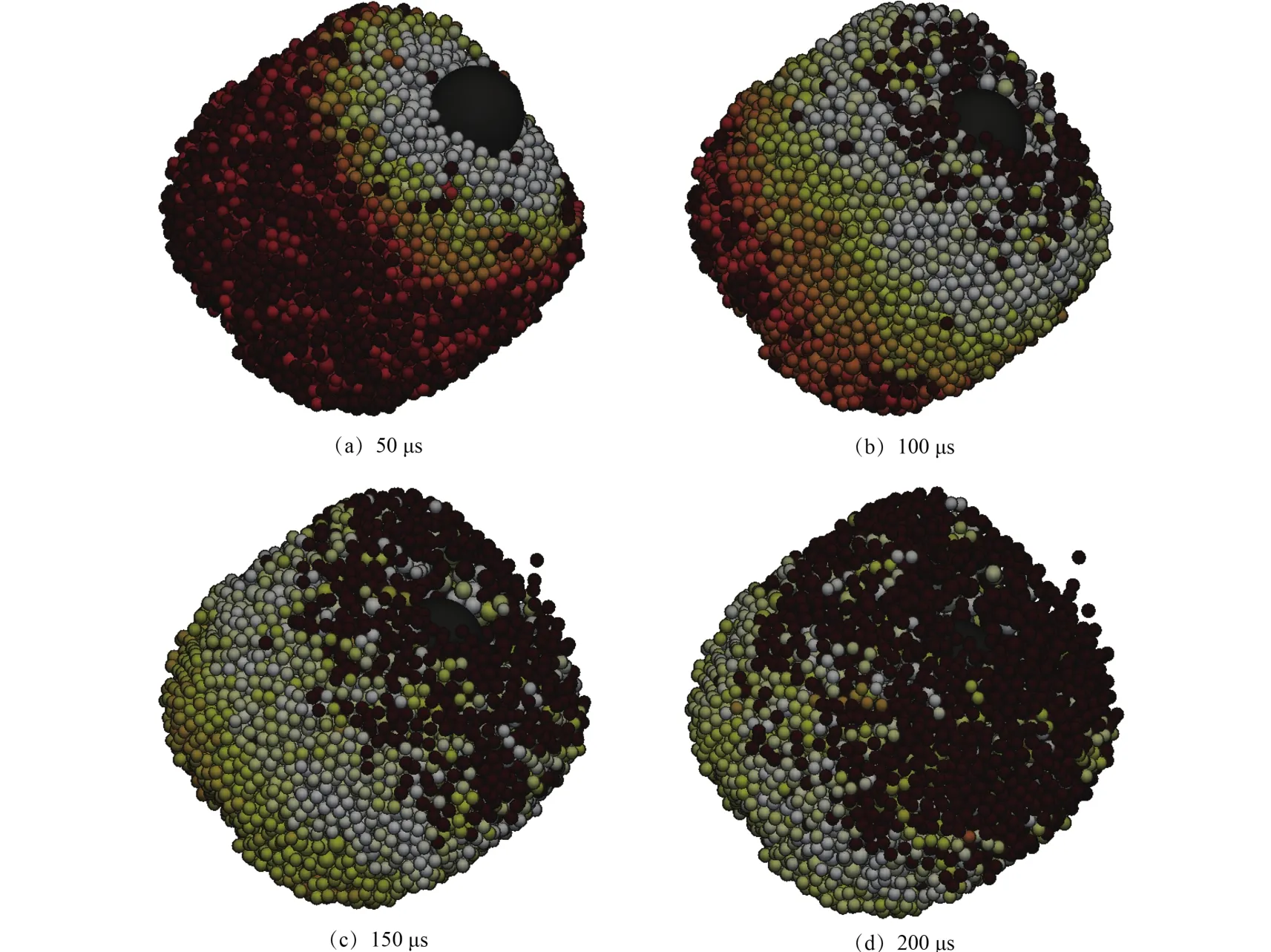
图 3 小行星101955 Bennu碰撞过程的颗粒受力分布Fig. 3 Calculation of the impact of the asteroid 101955 Bennu

由图 3（a）可见，小行星101955 Bennu受到其五分之一直径大小的球体碰撞初始碰撞时，小行星的星体上颗粒受力大小分布与颗粒和碰撞球体之间的距离有关，小行星表面相邻颗粒的受力大小比较接近，同时紧邻撞击物附近颗粒受力远远高于背离撞击区域。从图 3（b）和图 3（c）可见，随着碰撞的进一步深入进行，虽然球体已经逐渐进入小行星内部，但小行星表面颗粒的受力大小分布仍然和表面颗粒与初始碰撞接触时刻小行星表面碰撞点的距离有关，只是出现了一些受力大小与相邻颗粒受力大小相差较大的颗粒，但从小行星整体来看，小行星表面颗粒速度大小呈现出明显的分层特点，即初始撞击点附近颗粒由于被抛射出小行星本体，不再受到由于撞击而产生的冲击波的影响，受力迅速下降；而受力最大区域（白色区域）随着撞击物的深入逐渐沿撞击方向移动，最终完全贯穿小行星本体。将图 3（d）和图 3（a）对比可见，小行星受到碰撞后期的表面颗粒受力分布和碰撞早期的表面颗粒速度分布几乎完全相反，同时小行星表层颗粒在碰撞过程中由表面向内部逐层被完全抛射出小行星。

图 4给出了小行星101955 Bennu受到碰撞以后的碎石颗粒空间瞬时分布情况。碰撞以后，坐标轴x方向的碎石颗粒最大速度分量为449.191 929 2 m/s，最小速度分量为–368.694 478 2 m/s；坐标轴y方向的碎石颗粒最大速度分量为385.1557403 m s–1，最小速度分量为–328.650 189 7 m/s；坐标轴z方向的碎石颗粒最大速度分量为384.660 715 9 m/s，最小速度分量为–348.184 552 8 m/s。碰撞后碎石颗粒的速度的模的最大值为610.867 m/s，碎石颗粒的速度的模的最小值为21.775 49 m/s。

从图 4的碰撞以后碎石颗粒空间瞬时分布情况来看，以小行星五分之一大小的球体高速碰撞小行星，可以把小行星完全摧毁，撞击成大量碎石。以碰撞前小行星质心为坐标原点，最终碎石颗粒的速度大小约在数百米每秒量级，在该速度下，小行星碎片云无法在引力作用下重聚起来，因此可以认为该小行星已被完全摧毁瓦解，对地球的撞击威胁已基本降低到安全水平以下。这里需要特别指出，在实际的撞击过程中，碎石颗粒之间的碰撞破碎将会产生大量碎屑和粉尘，但由于计算机计算能力的限制，不能完全模拟出撞击产生的所有碎屑和粉尘的动力学行为，只能近似地计算出撞击后特定尺寸大小以上的碎石的动力学行为。

图 4 小行星101955 Bennu碰撞以后的碎石颗粒分布Fig. 4 Calculation of the impact of the asteroid 101955 Bennu

Lomov等[7]在2013年的研究中采用核爆的方式来炸毁潜在威胁的小行星，对于个头较大的小行星，例如数百千米量级的小行星来说，目前核爆的方法是摧毁这类小行星的唯一有效方法[7,19]。此外，对于事先并未发现的突然出现的将要撞击地球的几十千米以下量级的小行星，核爆的方法也能快速有效地将其摧毁。然而，核爆的方法摧毁潜在威胁的小行星也会产生大量碎屑和粉尘。同本文的结果不同的是，核爆的方式炸毁小行星产生的碎屑和粉尘具有强烈的放射性。这些具有强烈放射性的碎屑和粉尘以及个头稍大的碎石会向四面八方散开，一部分可能会进入地球大气层，对人类的生存环境造成难以估量的影响。

因此，Lomov等[7]研究的采用核爆的方式来炸毁将要撞击地球的小行星的办法，在针对数百千米大小的小行星或者事先未发现的突然出现的小行星方面，是万不得已的唯一办法。然而通常情况下，本文所采用的方法既能有效防御潜在威胁的小行星，又不对太空环境产生放射性污染，是两全其美的办法。

3 结 论

研究了针对潜在威胁的小行星的碰撞拦截问题。采用高精度多面体模型数据来建立小行星的形状与物理模型。采用碎石堆填充多面体模型来建立小行星的内部结构模型。研究以有较为精确的外形数据的小行星101955 Bennu为例计算了针对小行星的碰撞过程。使用一个大小为小行星五分之一的球状物碰撞小行星。研究表明：这种方式可以有效地将小行星撞成大量碎小的石块，可以用来对潜在威胁的小行星进行防御。

[1]Quarta A A，Mengali G. Electric sail missions to potentially hazardous asteroids[J]. Acta Astronautica，2010，66（9）：1506-1519.

[2]Chesley S R，Farnocchia D，Nolan M C，et al. Orbit and bulk density of the OSIRIS-REx target Asteroid（101955） Bennu[J]. Icarus，2014，235（1）：5-22.

[3]Saito T，Kaiho K，Abe A，et al. Hypervelocity impact of asteroid/comet on the oceanic crust of the earth [J]. International Journal of Impact Engineering，2008，35：1770-1777.

[4]Vardaxis G，Sherman P，Wie B. Impact risk assessment and planetary defense mission planning for asteroid 2015 PDC[J]. Acta Astronautica，2016，122：307-323.

[5]Michel P，Cheng A，Küppers M，et al. Science case for the Asteroid Impact Mission（AIM）：a component of the Asteroid Impact & Deflection Assessment（AIDA） mission[J]. Advances in Space Research，2016，57（12）：2529-2547.

[6]Cheng F A，Atchison J，Kantsiper B，et al. Asteroid impact and deflection assessment mission [J]. Acta Astronautica，2015，115：262-269.

[7]Lomov I，Herbold E B，Antoun T H，et al. Influence of mechanical properties relevant to standoff deflection of hazardous asteroids [J]. Procedia Engineering，2013，58（4）：251-259.

[8]Koenig J D，Chyba C F. Impact deflection of potentially hazardous asteroids using current launch vehicles[J]. Science & Global Security，2007，15（1）：57-83.

[9]Jiang Y，Baoyin H X，Li H N. Periodic motion near the surface of asteroids [J]. Astrophysics and Space Science，2015，360（2）：63.

[10]Wang X Y，Jiang Y，Gong S P. Analysis of the potential field and equilibrium points of irregular-shaped minor celestial bodies[J]. Astrophysics and Space Science，2014，353（1）：105-121.

[11]Popova O P，Jenniskens P，Emelyanenko V，et al. Chelyabinsk airburst，damage assessment，meteorite recovery，and characterization [J]. Science，2013，342（6162）：1069-1073.

[12]Brumfiel G.Russian meteor largest in a century [N]. Nature News. England，Macmillan Publishers Limited，part of Springer Nature，2013. doi：10.1038/nature.12438.

[13]Werner R A，Scheeres D J. Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia[J]. Celestial Mechanics and Dynamical Astronomical，1997，65（3）：313-344.

[14]Nolan M C，Magri C，Howell E S，et al. Shape model and surface properties of the OSIRIS-REx target Asteroid（101955） Bennu from radar and lightcurve observations [J]. Icarus，2013，226（1）：629-640.

[15]Nolan M C，Magri C，Howell E S，et al. Asteroid（101955） Bennu Shape Model V1.0 [Z]. NASA Planetary Data System 211. Los Angeles：University of California，2013.

[16]Jiang Y，Baoyin H X，Li J F，et al. Orbits and manifolds near the equilibrium points around a rotating asteroid [J]. Astrophysics and Space Science，2014，349（1）：83-106.

[17]Jiang Y，Zhang Y，Baoyin H X. Surface motion relative to the irregular celestial bodies [J]. Planetary and Space Science，2016，127：33-43.

[18]Schwartz S R，Richardson D C，Michel P. An implementation of the soft-sphere discrete dlement method in a high-performance parallel gravity tree-code [J]. Granular Matter，2012，14：363-380.

[19]马鹏斌，宝音贺西. 近地小行星威胁与防御研究现状[J]. 深空探测学报，2016，3（1）：10-17. Ma P B，Baoyin H X. Research status of the near-Earth asteroids' hazard and mitigation[J].Journal of Deep Space exploration，2016，3（1）：10-17.

通信地址：清华大学蒙民伟科技大楼北楼N904（100084）

E-mail：jiangyu_xian_china@163.com

Calculation and Analysis of the Impact Defense to the Potentially Hazardous Asteroids

JIANG Yu1,2*，CHEN Bin2，BAOYIN Hexi2，LI Hengnian1
（1. State Key Laboratory of Astronautic Dynamics，Xi’an Satellite Control Center, Xi’an 710043，China；2. School of Aerospace Engineering，Tsinghua University，Beijing 100084，China）

The dynamical problems of the asteroid defense are investigated by using the impact method. The polyhedron model isused to build the shape model of the asteroids, and the rubble-pile model is used to build the structure model of the asteroids. A sphere which has the same dense and material quality with the asteroid is assumed to impact to the asteroid, and the high velocity impact and the distribution of the rocks and rubbles after the impact are computed. Considering the contact deformation between the asteroid and the impact sphere, and the contact deformation inside the body of the asteroid among the rocks and rubbles which comprise the structure of the asteroid, the mutual gravitational force, the normal contact force, the tangential static frictional force, the tangential kinetic friction force, and the moment of rolling friction are calculated. Asteroid 101955 Bennu is used to calculate the dynamical behaviors of the impact defense of the potentially hazardous asteroids. The results show that the method of high velocity impact is useful for the defense of potentially hazardous asteroids, the asteroids can be crashed into a large number of rocks and rubble. The presented methodhas no pollution to the space environment. In this sense, the method is much better than the nuclear explosion method.

potentially hazardous asteroids；asteroid defense；asteroid impact；impact defense；rubble-pile asteroids

P185.7

A

2095-7777（2017）02-0190-06

10.15982/j.issn.2095-7777.2017.02.014

姜宇（1983– ），男，博士后，工程师。主要研究方向：太空目标碰撞与冲击动力学，多小行星系统动力学与探测，卫星星座与编队控制。

[责任编辑：宋宏，英文审校：朱鲁青]

姜宇，程彬，宝音贺西，等. 潜在威胁小行星碰撞防御的计算与分析[J]. 深空探测学报，2017，4（2）：190-195.

Reference format: Jiang Y，Cheng B，Baoyin H X，et al. Calculation and analysis of the impact defense to the potentially hazardous asteroids [J]. Journal of Deep Space Exploration，2017，4（2）：190-195.

2016-10-01

2017-04-09

国家自然科学基金资助项目（11372150）