一个关于常数e的逼近式
2017-07-03秦庆雄
秦庆雄
(漾濞县第一中学,云南漾濞672500)
一个关于常数e的逼近式
秦庆雄
(漾濞县第一中学,云南漾濞672500)
利用函数的单调性,可证明成立不等式:
并通过实例说明它在其他不等式证明中的简单运用。
杨必成-L.Debanth不等式;Carleman不等式;逼近式
1998年,杨必成和L.Debanth在文〔1〕(或文〔2〕)中给出了如下一个关于常数e的逼近式:

笔者经过探究发现,式(1)可以加强为如下定理,现行之成文,和大家一起来分享。
定理设整数n≥1,则有

证明:1)由于不等式

作辅助函数
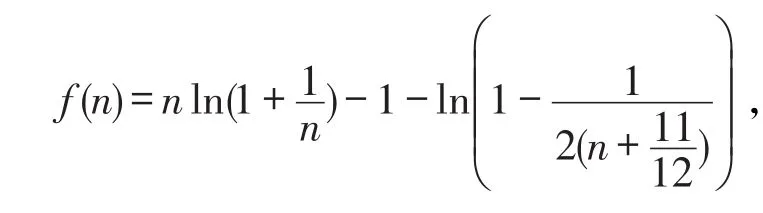
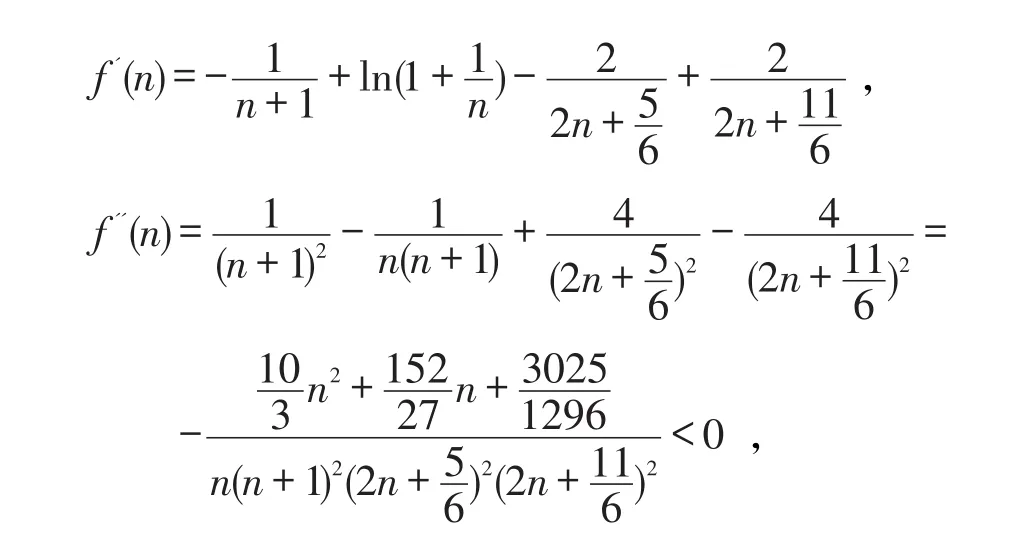
由上式知,f′(n)在[1,+∞)上单调递减。从而,对于任意都有据此,上单调递增,且对于任意都有
ln e-1-ln 1=0,即


所以,式(3)成立。
2)由于不等式

作辅助函数

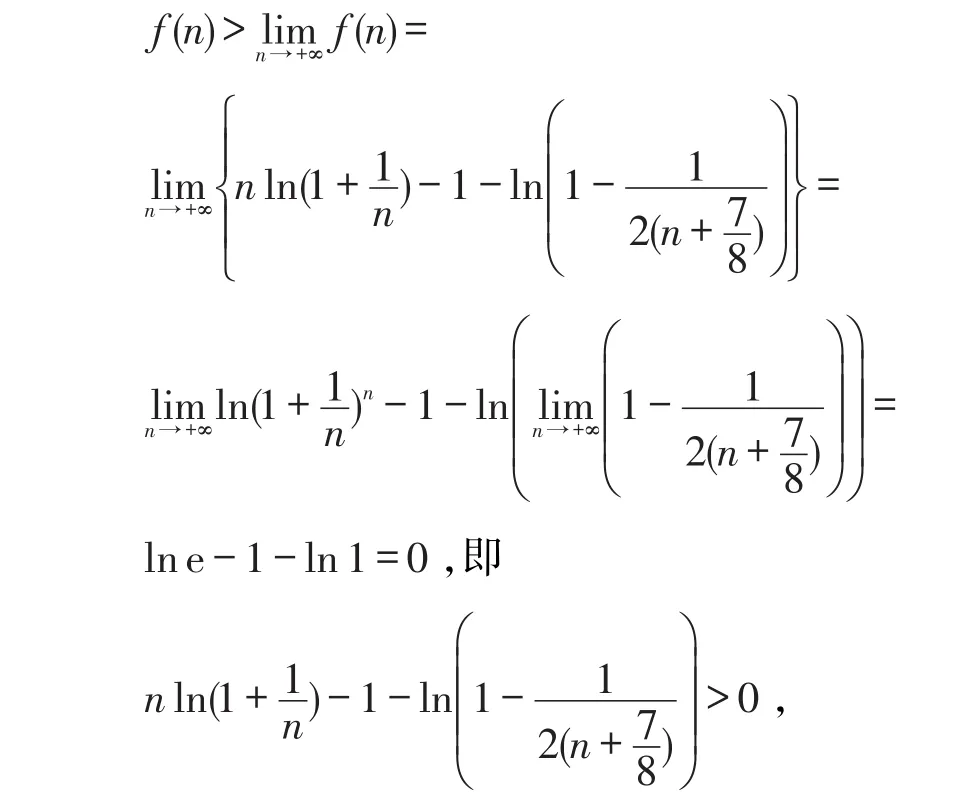
所以,式(4)成立。
综上,由式(3)和(4)知,式(2)获证。
最后,我们仅举两例,说明定理的应用。
例1设整数n≥1,则有

证明:由算术-几何平均不等式〔3〕,得


因此,要证
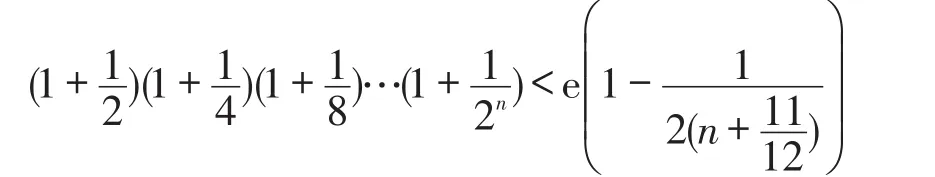
成立,
由式(3)知,上式成立。
所以,不等式
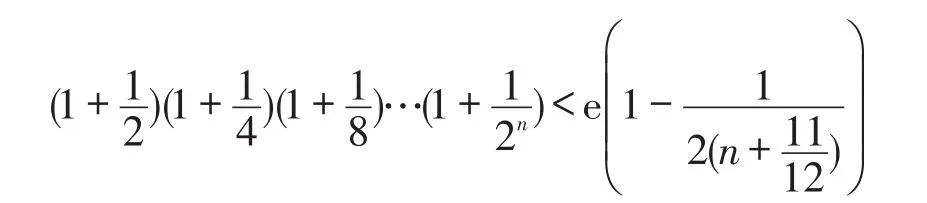
获证。

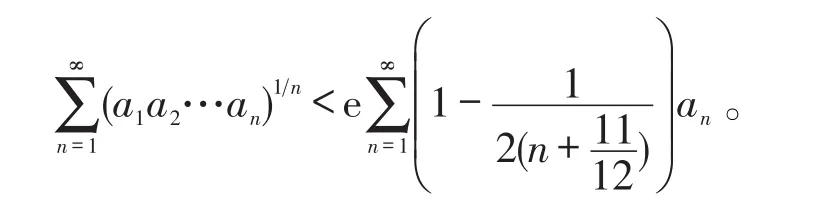
证明:由算术-几何平均不等式〔3〕,得
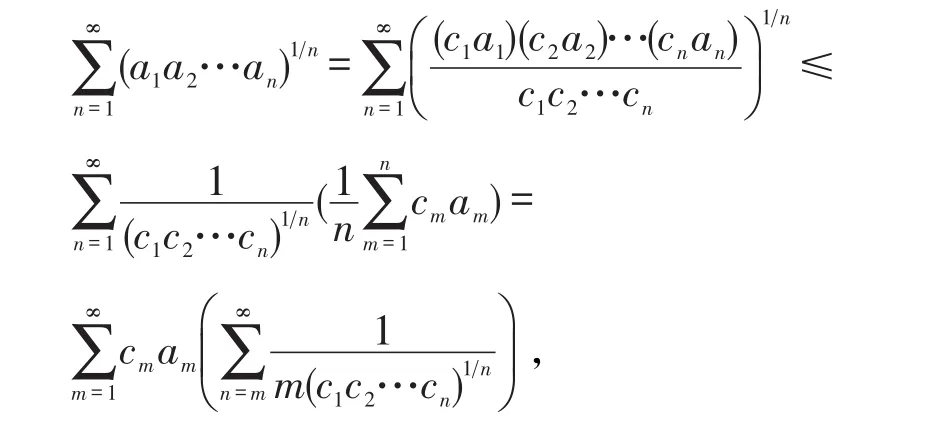
欲使内部的求和容易处理,我们选取

此时

从而,
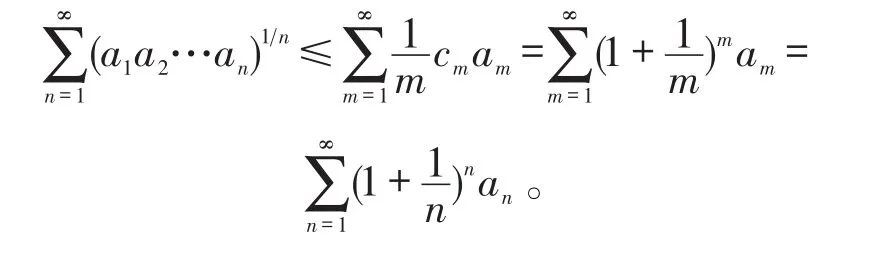
又由式(3),得
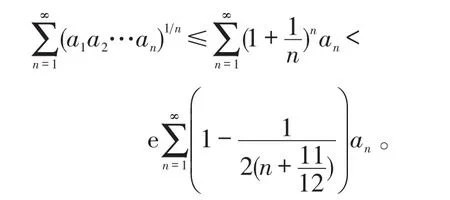
注:例2加强了文献〔1〕中已有的如下加强的Carleman不等式:
〔1〕YANG B C,DEBNATH L.Some inequalities involving the constante and an application to Carleman's inequality〔J〕. JMath AnalAppl,1998,223(1):347-353.
〔2〕王挽澜.建立不等式的方法〔M〕.哈尔滨:哈尔滨工业大学出版社,2011:368.
〔3〕HARDY G H,LITTLEWOOD J E,POLYA G.不等式〔M〕.越民义,译.北京:科学出版社,1965.
A Resulton the Approximation of Constante
Qin Qingxiong
(Yangbi NO.1 Middle School,Yangbi,Yunnan 672500,China)
Using the monotonicity of function,it can be proved that,where.Examples are given to show that this inequality can be used to prove otherinequalities.
Yang B C-L.Debanth's Inequality;Carleman's Inequality;approximation
10.3969∕j.issn.2096-2266.2017.06.004

O122.3
A
2096-2266(2017)06-0016-03
(责任编辑袁霞)
2016-05-18
2016-12-14
秦庆雄,中学一级教师,主要从事数学教育与中学数学,特别是不等式问题等研究.
