时滞耦合系统非线性动力学的研究进展1)

张 舒 徐 鉴

(同济大学航空航天与力学学院，上海200092)

时滞耦合系统非线性动力学的研究进展1)

张 舒 徐 鉴2)

(同济大学航空航天与力学学院，上海200092)

随着对自然界客观规律的深入认识，工程系统设计的精细化和复杂性要求也与日剧增.在许多耦合的动态系统设计过程中要考虑由耦合过程的时滞所引发的动力学行为，该时滞来自于与传感系统、作动系统和控制系统耦合的过程.耦合时滞也广泛存在于交通、系统生物学、电子通讯、神经和信息网络等技术中.本文首先从耦合时滞出发，在以时滞为中心的耦合系统复杂动力学机制、时滞镇定耦合系统的实验基础和实现、快慢变时滞耦合系统动力学和时滞神经网络同步和去同步4个方面，对耦合时滞诱发的动力学研究进展进行综述.着重介绍了时滞耦合系统中耦合时滞诱发的高余维分岔奇异性及新的定量分析方法、中立型时滞微分方程的规范型计算、具有耦合时滞的非线性系统中耦合时滞和非线性参数的辨识方法与实验实现、快慢变时滞耦合系统的张弛振荡、耦合时滞诱发的网络系统的同步模式切换等问题的研究进展；然后在应用方面重点介绍了车床磨削加工过程中耦合时滞诱发的颤振及其机理、具有惯性项和耦合时滞的神经网络系统中耦合时滞诱发的高余维分岔和复杂动力学、时滞动力吸振器与隔振装置的设计与实验实现.最后，从耦合时滞系统的一般性理论和工程应用两个方面展望了近期值得关注的一些问题.

时滞耦合系统，非线性动力学，时滞微分方程，快慢变系统，神经网络

引言

由于时滞在实际耦合系统中普遍存在，其已成为数学、力学、高精度机械制造工程、生物等众多领域科学家关心的重要课题.以非线性动力学领域的国际知名期刊《Nonlinear Dynamics》为例，其刊发的标题中包含“coupling delay”的论文，2002—2006年仅1篇，2007—2011年有7篇，2012—2016年多达52篇.说明这一课题的研究在国内外已经呈现上升趋势.

首先，当力学系统承受长期的外激励作用时，由于采用所有形式的时滞反馈(位置、速度、状态)控制都无法完全消除系统的振动,因此必须采用动态时滞控制器(基于微分方程建模)吸收系统所承受的外部激励能量，从而实现抑制振动的目的.且采用动态的非线性时滞控制器可以在更宽的频带范围内吸收系统所承受的能量.动态控制器对系统的作用与时滞反馈控制明显不同.从作用效果看，时滞反馈控制器是单向作用，时滞效应也是单向的，而动态时滞控制是双向作用，时滞效应也是双向的；从模型上看：对于一个简单的位置或者速度反馈时滞系统，状态维数只与目标系统状态有关，且常常较低.而时滞耦合系统的状态维数与子系统的状态维数有关，因此时滞耦合系统的状态维数常常是高维的，耦合的子系统越多，状态维数越高.这些都给研究工作提出了新的挑战：第一，以此方式建立的振动控制系统将是高维的时滞和非线性耦合系统，在考虑设计参数时，至少需要涉及时滞量和控制器与系统的耦合强度两个参数，这就需要分析系统更高余维数的奇异性，特别要分析时滞和耦合强度这两个参数与系统发生强共振之间的关系，迄今为止该问题在国内外学术界没有得到解决；第二，在力学系统特别是机械系统中，如何实现控制器与系统之间的非线性和时滞耦合；第三，如果采用分段线性来模拟非线性，存在的问题就是很难用理论方法分析时滞非光滑耦合系统，只有通过实验解决；另外，变时滞和变参数系统动力学的研究手段有限，也只有通过实验总结各种变时滞对耦合系统的影响规律；第四，如果控制器的质量与系统的质量的比值是小量，将形成快慢变时滞耦合非线性系统，目前仅得知张弛振荡是无时滞快慢变耦合系统明显的特征之一，在生命系统中表现的形式是所谓的spiking动力学行为，但是对快慢变时滞耦合非线性系统动力学行为的了解甚少；第五，以此方式建立的振动控制系统是通过共振的方式进行能量交换的，从网络系统的观点出发，这种能量传递成功与否就是网络的同步与去同步问题，目前，从网络系统观点出发研究振动控制的工作也甚少.

其次，除了受控力学系统中控制环节存在时滞外，许多耦合系统在耦合过程中，子系统之间的耦合因素(力、电位信号等)也存在着作用或者传递过程中的时间滞后.例如，在砂轮磨床这样简单的系统中，通过砂轮与工件接触点的作用与反作用力实现耦合，反作用力产生于工件再生和砂轮再生过程，可以表示为工件和砂轮位置的函数，其中工件和砂轮再生过程存在一定程度的时滞，它们与工件和砂轮的转速有关，现代精密高效加工技术要求设计出适当的转速使系统不出现再生颤振，从而提高工艺质量.因此砂带磨削过程中的磨削参数的测量和优化非常重要，时滞成为重要的设计参数.类似的工艺要求也会出现在高精度钻孔、打磨和切削等设备中.除了力学系统之外，近年来，医学工程中人机耦合交互系统的有效性、激光阵列耦合系统的协同性、耦合人工神经网络系统的同步和去同步性、网络拥塞和交通工程中车流堵塞的规律性等也受到了特别关注，主要原因是认识和了解这些力学或者物理系统耦合过程中时滞诱发的动力学性质，可为这些系统的设计提供更加准确的依据.例如，即使最简单的单向车流跟随模型也是一个时滞耦合系统.事实上，在单向车辆跟随过程中，当前的车辆速度与其前面若干车辆过去一段时间的速度有着密切的关联，此处的“过去一段时间”就是时滞.显然，该时滞是一个综合因素，取决于行驶方向道路的质量、车辆的性能和司机的反应能力.从直观上可以看出,这种时滞会影响整个车流行驶的平均速度，从而成为车流是否堵塞的一个重要因素，按照这个观点构造的车流模型是一个多时滞耦合的系统，特别应该注意到，如果车流中车辆的性能差异较大，即部分车辆对环境(包括其他车辆)变化十分敏感，而另一部分车辆则比较迟钝，体现在模型上便表现为不同的车辆模型右端的尺度不同甚至差异很大，此模型就是快慢变时滞耦合系统.

最后，受控时滞系统的复杂运动具有特殊性，由于控制策略总是对某个特定的动力学行为(例如平衡态或者周期运动)进行控制，因此，在一定条件下，受控时滞系统中的时滞不会诱发 Zero-Zero和Zero-Pair等分岔行为.然而，研究结果表明，对于耦合时滞系统，存在上述分岔行为，这就意味着时滞耦合系统可以通过这样的机制产生同宿或者异宿轨道分岔，使其动力学行为较受控时滞系统更加复杂.可能存在的同宿和异宿轨道表明，时滞耦合系统中的时滞可以导致孤子解.从理论上看，时滞耦合系统的问题涉及高维时滞微分系统，这对研究提出了更大的挑战.因此，对时滞耦合系统的研究也符合从简单走向复杂、从特殊走向一般、从低维到高维的基本认识规律.

综上所述，本文将对 4个方面的科学问题进行综述，即以时滞为中心的耦合系统复杂动力学机制、时滞镇定耦合系统的实验基础和实现、快慢变时滞耦合系统动力学和时滞神经网络同步和去同步，其核心科学问题就是时滞耦合系统的非线性动力学理论与应用研究.该研究不但可以深刻认识耦合系统中客观存在的时滞对系统各种动态性质的影响，而且可以为此类系统的设计或者识别客观存在的时滞提供理论依据和参考，因此具有重要的科学意义.由于时滞耦合动力系统的初值空间是无限维的，从而解空间也是无限维的，因此，时滞耦合系统动力学的研究也是极具挑战性的研究课题[13].

1 以时滞为中心的耦合系统复杂动力学机制

近年来，以时滞为中心的耦合动力系统成为越来越重要的研究对象，主要原因在于精密加工等高技术需求、解决交通堵塞等社会需求和系统生物学发展的科学需求等使得系统耦合过程中的时滞不能被忽略.为了更好地理解时滞对耦合系统的影响，需要从理论上研究时滞与各种动力学甚至复杂动力学行为的关系，以便更加深入地认识自然界客观存在现象的原因和机制或者对耦合系统进行优化设计.因此，以时滞反馈为中心的耦合系统动力学行为分类研究成为重要的课题.目前的研究主要关注稳定性分析、分岔分析、复杂动力学或者奇异性分析等，且大部分的工作还停留在稳定性分析方面，对于分岔分析和复杂动力学机制的研究还不多，存在一定的难度.

研究表明，当考虑耦合系统耦合过程中的时滞时，系统平衡态的稳定性常常依赖于耦合时滞.针对双向再生圆柱形磨削加工系统，Liu和Payre[4]提出了一种分析耦合时滞系统平衡态稳定性的计算方法，该方法可以计算出位于复平面虚轴上的特征值，并据此判断系统平衡态是否可能失去稳定性而出现再生颤振.利用特征值与系统参数的关系，可以得到避开再生颤振的设计参数.对于交通堵塞问题，已有简单的单向车流跟随时滞系统模型[5]，并且对于离散时滞和连续分布时滞模型进行了初步的稳定性分析，得到了这种单向车流稳定的依赖时滞的参数区域.同济大学和南京航空航天大学的项目组，从控制系统稳定性的观点出发，也对受控时滞系统的稳定性特别是相关理论在实际问题中的应用做了大量的研究，关于这方面的工作可以参考相关的综述[6-7].

近年来，由于分岔软件DDE-BIFTOOL的发布，该软件被一些学者应用于从数值角度分析时滞诱发的复杂现象.Erzgraber等[8]研究了内部具有滤波的半导体激光器的动力学和分岔.光谱通过内部过滤器后重新进入激光输入，而在对光谱滤波时会出现时滞，于是其变成一个耦合时滞系统的动力学与分岔问题.由于此类激光器输出是一些特定光谱的激光，要求精度较高，涉及到滤波时的时滞对输出的影响.在设计过滤器时，由于时滞难以避免，然而强度往往可以调节，因此，为了方便设计需要考虑时滞和强度参数对动力学的影响，这是一个典型的时滞诱发的余维2奇异性及其导致的动力学行为的分类问题.通过软件DDE-BIFTOOL,作者给出了SN-Hopf和BT分岔及其分类，尽管没有严格的理论证明，但该结果展示了余维2分岔分类重要的科学和工程意义.同样的研究思路也被Green[9]用于一般的光学反射激光发生器中.

综上所述，由于时滞诱发的高余维奇异性具有重要的应用背景，引起了许多从事理论研究学者的兴趣.由于高余维奇异性的理论分析具有很大难度，因此从事这方面研究工作的学者不多.加拿大数学家Campbell领导的课题组是长期从事这方面研究的团队之一，该团队主要采用中心流形约化，研究的对象都是低维的时滞系统[10].近期有研究发现，随着状态空间维数的增加，时滞诱发的高余维分岔问题若采用中心流形约化将会变得非常复杂，而且还存在数学的开折参数与物理参数无法建立对应关系的缺陷.为了解决上述问题，学者们提出了一些新的方法，例如摄动--增量方法，该方法不但可以用于研究状态变量是高维的耦合系统的Hopf分岔[11]，也能对低维耦合时滞系统的Hopf-Hopf分岔的奇异性及其动力学行为进行分类[1213].

另外，Hamilton是力学中的一类非常重要的系统，已取得了丰硕的研究成果.当前值得关注的是拟Hamilton系统，即Hamilton系统的小扰动系统.研究这类系统的直接动机来自这样的事实：许多复杂系统可以看作是某些较简单系统的小扰动，并且一般扰动系统所产生的无扰系统不具有的动力学性质常常对应分岔解附近的情况.另外，在适当的坐标系下，在Hopf分岔、Hopf-Hopf分岔等分岔点附近的系统即可看作拟Hamilton系统.即使扰动项非常小，也可能引起动力学性质产生本质性的巨大变化.研究时滞对Hamilton系统的影响既有重要的理论价值，又是极具挑战性的研究问题,这方面的工作,朱位秋研究小组的成果处于国际领先地位[14].

目前对于时滞耦合系统的研究主要停留在稳定性分析方面，对于时滞诱发的时滞耦合系统的高余维奇异性及其分岔分类还需要理论分析和方法的创新.具体有以下几个问题需要解决：研究和发展时滞耦合系统新的约化方法，重点研究在强时滞耦合和多时滞耦合条件下局部动力学特征表现的定量化方法，从而发展时滞耦合系统动力学行为描述的计算方法；研究针对时滞耦合系统的时滞和耦合强度诱发的弱共振和强共振动力学特性的一般性方法，在此基础上研究时滞诱发的耦合系统动力学行为的奇异性及其动力学行为分类；研究时滞耦合系统中时滞和耦合强度诱发的各种其他高余维分岔及其相应的动力学定性分类，包括BT,Bautin,SN-Hopf,PFHopf,Fold-Hopf和PF-Hopf-Hopf分岔等；研究时滞耦合系统可能出现的新的复杂动力学及其形成的机制.下面对已取得的研究进展进行具体介绍.

时滞耦合系统的子系统之间出现内共振是通过各个子系统的固有频率进行能量交换，使得系统表现出特殊的动力学现象，其理论问题的本质是对时滞诱发的Hopf-Hopf分岔问题的研究，相应的现象是满足内共振关系的线性系统和不存在内共振关系的非线性系统所没有的，因此，研究内共振引起的动力学行为与系统中具有重要作用的参数之间的关系不仅具有重要的理论意义，还具有很大的应用价值.由于研究这样的时滞耦合效应还没有成熟的研究方法，首先需要对一个一般性的时滞耦合系统提出构造性方法.

设一般性的时滞耦合系统为

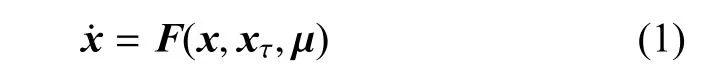
其中，x ∈ C([-τ,0],Rn)，µ =(µ1,µ2,τ)∈ R3是参数向量，xτ=x(t-τ)是时滞项，表示τ时刻以前的状态变量.为了更好地理解模型(1)，考虑具有时滞耦合的FitzHugh-Nagumo(FHN)模型[15]

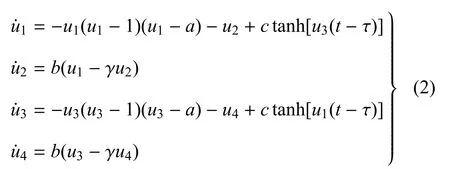
其中，u1和u3是膜电位，u2和u4是回复量，τ＞0是传输时滞，c为耦合强度,a,b和r为正常数.研究表明,参数耦合强度和时滞可以诱发Fold-Hopf分岔，可能导致系统出现周期运动、概周期运动、甚至混沌，如图1所示.这表明耦合系统可以通过改变时滞而表现出完全不同的动力学行为，其现象十分丰富，例如上述系统可以产生10种不同拓扑结构的动力学行为.

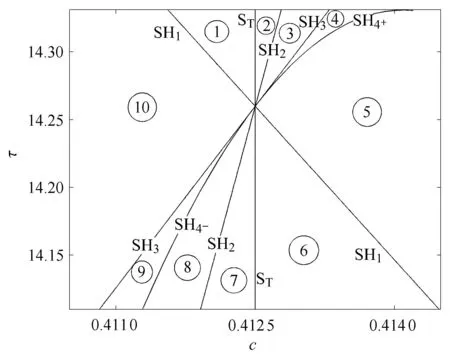
图1 时滞诱发模型(2)在参数平面发生分岔(其中a=0.1,b=0.01,γ =3.2,c0=0.4125,τ0=14.2564)Fig.1 Delay-induced bifurcation of(2)in the parameter space(c,τ)for a=0.1,b=0.01,γ =3.2,c0=0.4125,τ0=14.2564

当式 (1)在平衡点的两个特征值满足 Reλ1=Reλ2=0和 Imλ1：Imλ2(ω1：ω2)=k1：k2时，如果k1：k2是无理数，则式(1)可能出现非共振的奇异性;如果k1：k2是有理数，则式(1)可能出现共振的奇异性，分别对应非共振的双Hopf分岔和共振的双Hopf分岔.时滞多尺度方法在于将时滞τ也分解成多个时间尺度，即 x=x(T0-τ0,T1-τ1,T2-τ2,···)，其中 Tk= εkt,τk= εkτ (k=0,1,2,···)，于是式 (1)解的形式为

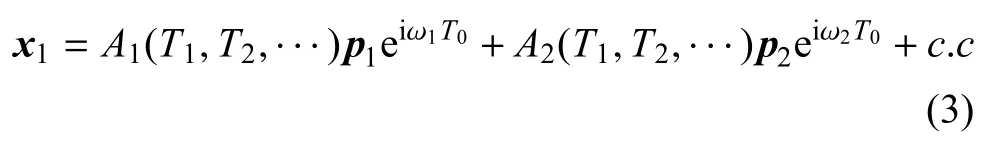
其中，A是复数，c.c表示前面项的共轭.通过消除长期项得到可解性条件，可以分别得到非共振和共振情况下复数形式的振幅--频率方程.Wang等[16]应用该方法研究了两个具有时滞耦合的Van der Pol振子.通过选择适当的参数，发现系统会发生1：3共振双Hopf分岔，并且对其在共振点附近的动力学行为进行研究，得到了振幅随参数变化的分岔图.结果表明,在两个具有时滞耦合的Van der Pol振子的1：3共振点附近存在丰富的动力学行为，如振幅死区、周期解、概周期解和周期三现象等.根据一般性的双 Hopf分岔理论，1：3共振属于共振双 Hopf分岔中的低阶共振问题，而对于其他共振问题，Wang等[17]得到了高阶共振是弱共振的结论，这是由于高阶共振的共振项出现在高阶项(高于三阶)，因此，模态之间的耦合较弱.然而这并不意味着低阶共振就是强共振，事实上如果一个低阶共振的所有低阶共振项的系数都为零，则该共振就是弱共振.在强共振情形，共振项首先出现在低阶项中，因此即使截断规范型方程到低阶项，发生内共振的两个模态之间的相互作用仍然比较强，这种相互作用使系统能量在两个模态之间相互传递.他们进一步得到了1：1，1：2和1：3三种低阶共振发生强共振和弱共振的条件.例如对于形如式(1)的时滞系统，得到时滞诱发的1：3内共振具有如下形式

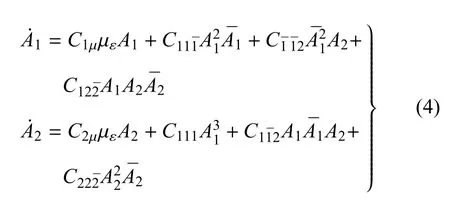
其中，C¯1¯12A2和C111A是共振项.Wang等[17]从理论上证明了如下结论：如果复振幅方程(4)中共振项的系数C111和/或C¯1¯12不等于零，则该1：3共振双Hopf分岔是强共振双Hopf分岔，其规范型方程是一个三维的系统；如果复振幅方程(4)中共振项的系数C111和C¯1¯12同时等于零，则该1：3共振双Hopf分岔是弱共振双Hopf分岔，其规范型方程是一个二维的系统.本文作者也讨论了1：1和1：2内共振强和弱的条件.为了区分强弱内共振的不同，考虑具有时滞反馈的极限环系统

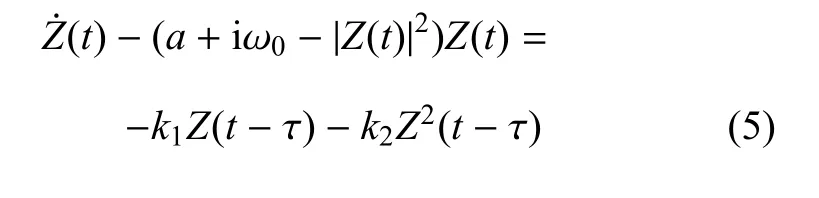
其中，Z(t)=x1+ix2是复数，ω0是振子的固有频率，a是实数，τ≥0是反馈时滞，k1和k2分别是线性和非线性反馈的强度.利用得到的强和弱共振的充分条件得知k2=0和k2≠0时，系统平凡平衡态发生1：2弱共振和强共振，系统(5)的幅频响应分别可以表示为和这里可以看出前者对应的分岔是余维3的，而后者是余维2的.

从上述分析结果可以看出，强共振和弱共振的动力学行为在本质上是不同的，并且不可互相替代，强共振双Hopf分岔具有余维3奇异性，而其他情形的共振双Hopf分岔具有余维2奇异性.该结论对双Hopf分岔点附近的动力学行为分类具有重要的指导意义，可以对如振幅死区、倍周期运动、周期三和概周期运动的机理提供合理的解释.作为一个直接的应用，Song等[1819]分别对多时滞神经网络和具有分布时滞的神经网络的双Hopf分岔进行了研究，解决了这3类网络动力学行为的分类问题.

多自由度时滞振动系统的一般形式为

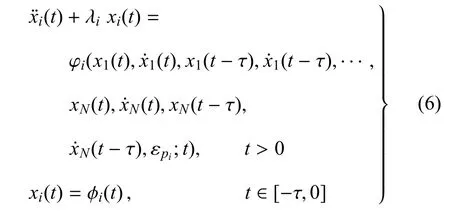
其中 xi∈ R，i=1,2,···,N，φi关于时间变量 t满足2π 周期性.定义连续算子 xit：xit(θ)=xi(t+θ),∀θ∈[-τ,0]，则 xit∈ C([-τ,0],R),i=1,2,···,N，其中C([-τ,0],R)表示从 [-τ,0]到 R的连续函数的全体所构成的空间.方程(6)从严格数学意义上讲为C空间上的泛函微分方程组，其形式为

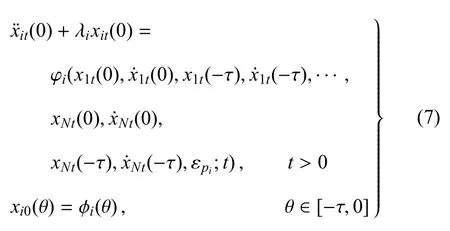
能够证明上述方程的解可以通过下面的迭代程序得到[20]

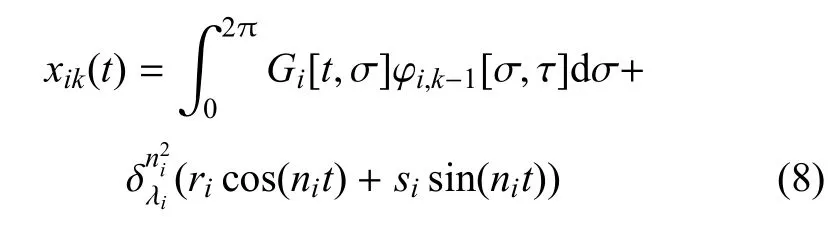
为了验证上述积分迭代解的精度和有效性，分别研究如下的单自由度和双自由度的时滞振动系统

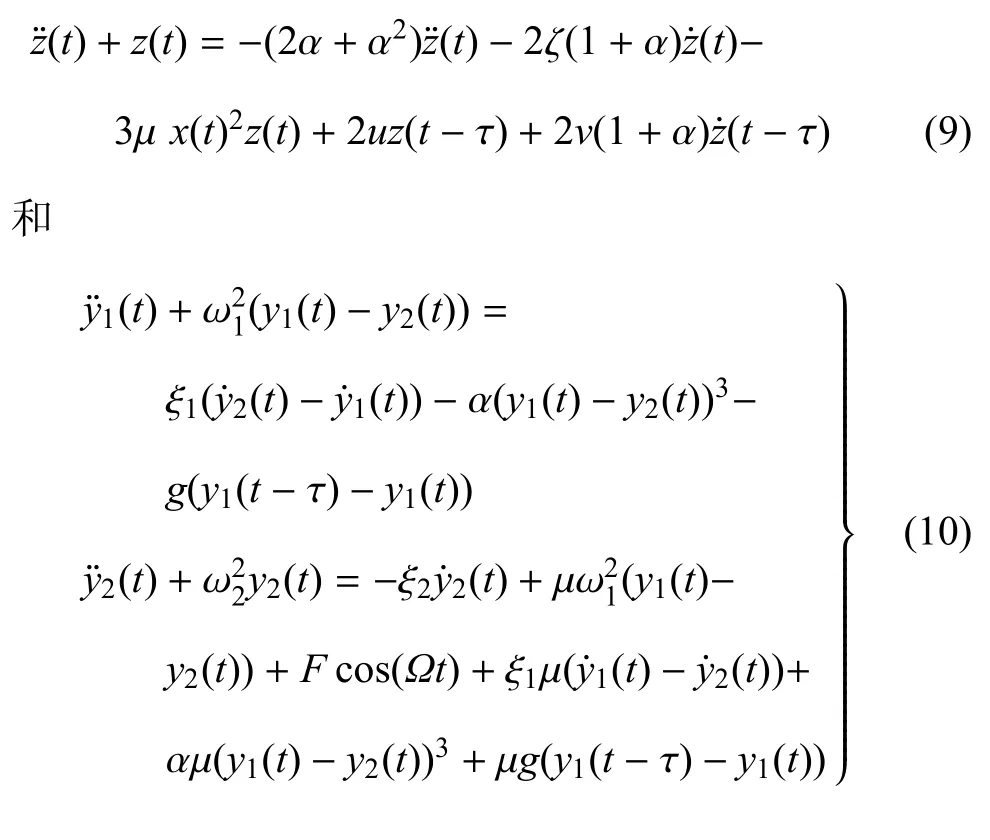
其中，ω1=ω2+σ1,Ω=ω2+σ2，并分别得到得到积分迭代法(integral iteration method，IIM)、多尺度方法(method of multiple scales，MMS)与数值解(numerical simulation)的幅频关系，如图2和图3所示.

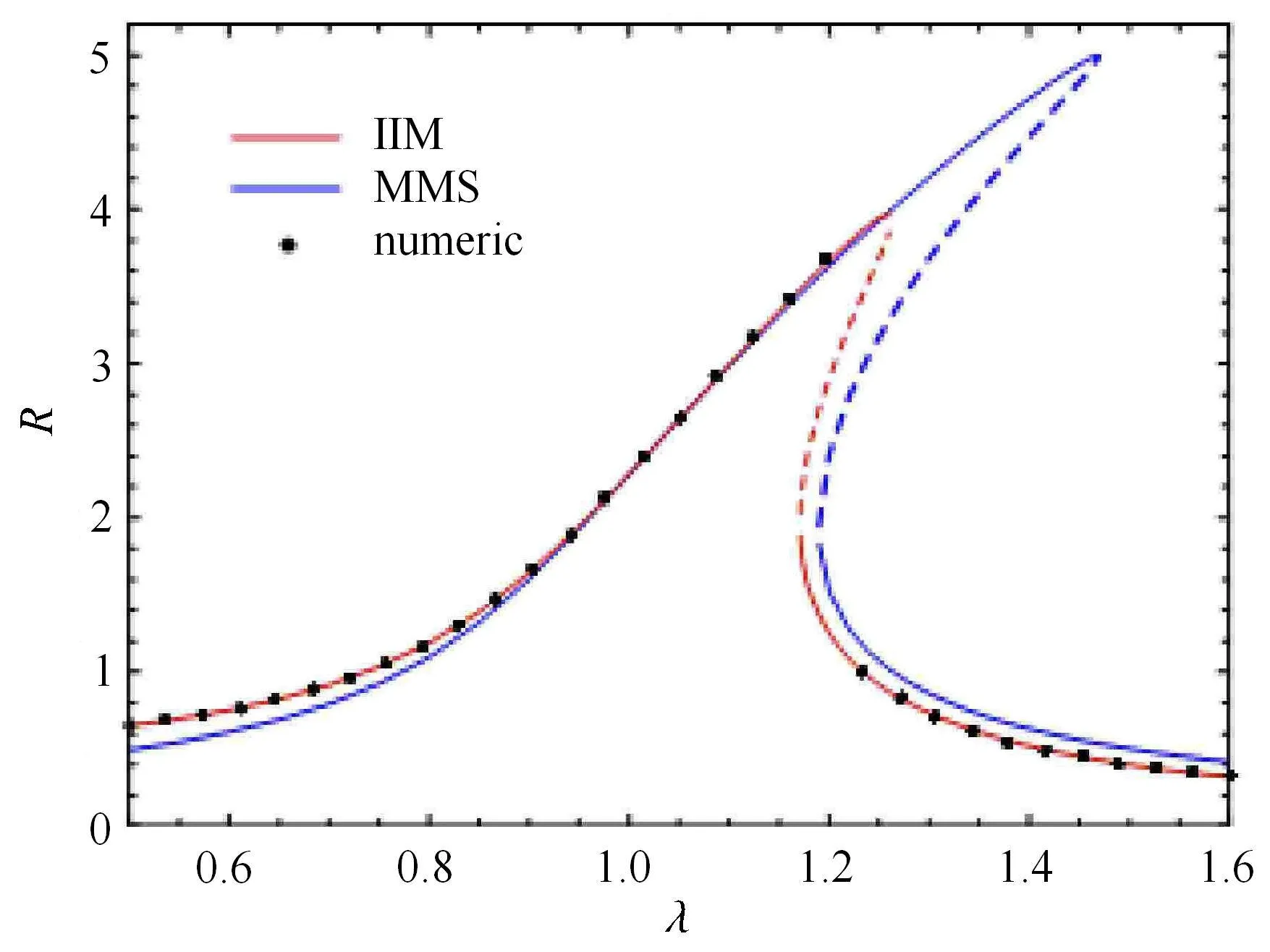
图2 方程(9)的幅频响应(τ=0.1,ζ=0.05,µ=0.05,f=0.5,u=0.05,v=-0.05)Fig.2 Amplitude-frequency response of Eq.(9),where τ =0.1，ζ=0.05,µ=0.05,f=0.5,u=0.05,v=-0.05

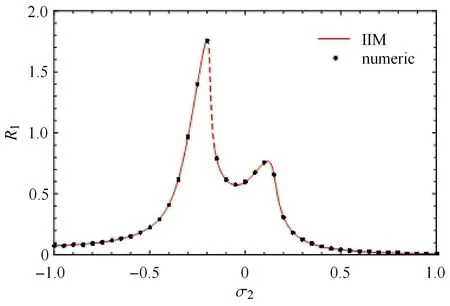
图3 方程(10)的幅频响应(ω1=1,ω2=1.2,σ1=-0.2,µ=0.1,ξ1=0.1,ξ2=0.1,F=0.1,α =0.2,g=-0.1,τ =0.2)Fig.3 Amplitude-frequency response of Eq.(10),where ω1=1,ω2=1.2,σ1=-0.2,µ =0.1,ξ1=0.1,ξ2=0.1,F=0.1,α =0.2,g=-0.1,τ=0.2

通过与数值结果比较，发现积分迭代法得到的结果与数值结果吻合得非常好，并且在很多情况下积分迭代法的精度比多尺度方法高.因此，积分迭代法是一种有效处理时滞振动问题的方法.

时滞的出现可能使得稳定性分析、响应计算、非线性分析都变得很困难.当时滞较小时，可将时滞项按Taylor公式展开，但这种方法不可靠.当时滞较大时，这种展开对动力学分析通常是无效的.Li等[21]研究了周期激励下具有较大时滞的时滞振动系统主共振解和亚谐共振解的稳定性，利用一种特殊函数(Lambert W)给出了一种计算最大Floquet乘子的直接方法，易于理解且计算精度高，由Floquet乘子实部的符号即可确定共振周期解的稳定性.另外，在时滞系统稳定性分析与Hopf分岔存在条件的讨论中都需要确定处于临界状态的特征根分支曲线随参数变化跨越虚轴的方向，尽管数值计算可以得到各具体临界点处的性态，但无法得到不同临界点处的普遍性结论.针对参数依赖时滞的一类系统，Wang[22]提出了一个简洁的计算公式，由临界稳定条件确定两个易于得到的辅助函数，计算其雅可比行列式即可.

Hopf分岔是时滞系统中导致平衡点失稳的一种典型的非线性动力学现象，其分析通常都是非常繁琐而复杂的.为了克服这一困难，在Maple软件环境下，Zhang等[23]实现了计算滞后型泛函微分方程在Hopf分岔附近的规范型的Maple算法和计算程序的开发，只要提供时滞微分方程的基本信息，即可得到规范型，应用非常方便.该算法的优点是可以同时对系统进行中心流形约化和规范型计算.中立型时滞系统与滞后型时滞系统相比，不仅动力学行为更复杂，理论分析也更困难.国际著名学者Nayfeh在2008年一篇论文中曾猜测：应用多尺度法和规范型理论对NDDE进行规范型分析时，所求得的规范型是相同的.Zhang等[24]同时提出了一套基于规范型理论的符号算法，用于中立型时滞微分方程的Hopf分岔的规范型计算，并应用该算法对受时滞位移反馈控制的起重机动力学进行了分析，研究结果验证了Nayfeh的猜测.

作为时滞耦合系统中时滞诱发复杂性的一个应用，Yan等[25]研究了磨削过程中的颤振机理.系统的力学模型被视为两端简支的欧拉--伯努利梁和阻尼弹簧质量系统的耦合系统,磨削系统的时滞来源于工件与砂轮接触一周的时间，他们首先分析了时滞诱发的失稳区间，重要的发现是存在着两个临界时滞分别对应着超临界和亚临界Hopf分岔，于是证明了Bautin分岔点(余维2)的存在.通过对Bautin奇异性的分析和动力学行为的分析，在理论上给出了静平衡态和颤振共存的判据，并且得到了响应的时滞区间，这意味着在静平衡态和颤振之间有一个转速的过渡区，这个过渡区依赖于系统的初始状态，也是可控的区间.研究结果有助于理解磨削加工中再生颤振的产生机理，且有助于抑制磨削过程中砂轮和工件颤振的转速设计.在此工作的基础上，Yan等[26]进一步讨论了往复式磨削中的颤振运动.相比于切入式磨削过程，往复式磨削中的砂轮会沿着工件轴向来回移动，从而保证工件的表面能够被完整地磨削.因此，其动力学控制方程中代表砂轮位置的参数不再是一个常数，而是转化为一个随时间变化的量.然而，考虑到砂轮作往复式运动的速度非常小，故将控制方程中砂轮的位置看作一个准静态的参数，得出了砂轮和工件分别稳定的条件，结果发现砂轮位置对砂轮自身的稳定性并没有很大的影响，但对于工件的稳定性却起着决定性作用.此外，其还发现在磨削过程中砂轮低阶模态的振动比高阶模态更容易被激发，且随着磨削刚度的变大，越来越多的高阶模态振动会被再生效应激发起来；当砂轮处于工件的中间位置时其自身的稳定性最差，而当砂轮向工件两边靠拢时其稳定性逐渐变好；同时着重考虑了砂轮位置对颤振运动的影响.结果表明,该参数对砂轮失稳引发的颤振几乎没有影响，而对工件失稳引发的颤振影响较大.当砂轮处于工件中点时，工件的颤振运动具有最大的振幅，而在砂轮远离工件中点的过程中,其振幅会逐渐减小直到消失.进一步将准静态的参数动态化，结合得到的分岔图追踪砂轮的位置和颤振的振幅，构造出了往复式磨削加工中可能发生的颤振运动，与直接用数值积分得到的结果吻合很好.此研究还发现在磨削过程中，由砂轮失稳引发的颤振具有持续性而由工件失稳引发的颤振运动则具有间隙性.

更进一步的应用是针对具有惯性的时滞耦合系统展开的.事实上，所有的振动耦合系统都可以看成是具有惯性项的双向神经网络系统.开展这样的研究有助于从一个新的视角认识工程实际系统或者动力学系统.Ge等[2729]应用上述研究中给出的判定强共振或弱共振的条件，确定了时滞参数诱发的弱共振余维2分岔的范围以及出现分岔点的参数值，对余维2共振分岔点邻域内的动力学行为进行了详细的分类讨论，证明了弱共振诱发的动力学行为最多只有6种，值得指出的是，其中出现的动力学死区、单模态动力学行为及其转换的行为，对工程中的振动抑制以及振动的能量转移有重要的参考价值，也构成了后续振动抑制研究工作的理论基础.

作为对时滞耦合系统的拓展研究，Jiang等[30]、Song等[31]分别考虑具有时滞耦合的神经网络系统和具有惯性特征的神经元时滞耦合系统，得到了在不同时滞耦合下系统参数平面内的鞍结分岔以及Hopf分岔曲线，发现了这两类分岔曲线在时滞较大时是相切的，通过分析，判断出相切点处即为余维2的BT分岔点，从理论上分析了此类BT奇异点附近的动力学特征，并且得到了从BT奇异点引出的同宿轨分岔曲线的局部表达式.Song等[32]进一步研究发现,该分岔曲线最终消失于一条鞍结分岔曲线，从而又得到另一个余维2的分岔曲线，即SNH分岔点.Song等[33]还发现,对不同的时滞耦合强度和周期性外激励，时滞耦合神经网络的动力学行为呈现出Circle/Circle,Circle/Homoclinic,SN/Circle and SN/Homoclinic和Fold/Hopf动力学模式.当增大周期外激励的强度时，由于系统的鞍结分岔以及Hopf分岔的存在，系统就会具有Fold/Hopf模式，此时系统的静止状态的产生(或消失)是通过Fold分岔得到的，而周期峰放电则是通过Hopf分岔产生或消失的.

在工程应用研究方面存在两个典型的问题，分别是时滞对轴流压气机喘振和人--桥耦合颤振模型的影响.在压气系统中,针对压力上升和空气扰动之间总有一定的时间滞后的基本特征，陈振等[34]重建了时滞MG模型，并通过研究发现,时滞会对喘振现象产生本质影响，即存在着临界时滞.当时滞小于临界时滞时，压气机的不稳定工作形式是大振幅的喘振状态；当时滞大于临界时滞时，压气机工作在旋转失速状态.针对千禧桥现象，以桥上行人为节点并考虑行人对桥作用有延时.Zhen等[3536]建立了桥梁侧向移动与行人之间耦合的力学模型，提出行人的延时作用是千禧桥侧振的主要因素的独特学术观点，并建立了相应的时滞动力学模型,模型的定量分析与目前存在的实验结果吻合较好，.在这个动力学模型的基础上，Zhen等[37]还给出了移动物体行驶诱发侧向移动的临界速度.

2 时滞镇定系统的实验基础和实现

多数情况下时滞被视为是控制系统中的不利因素，它不仅降低控制系统的控制效果，而且给系统带来不稳定性.因此，一般情况下时滞是控制系统中要求被减小或排除的因素.然而，国内外以往的研究表明，对于受控时滞系统，由于理论上发现的时滞导致的稳定性切换现象[38]及其开关作用[39]，使得通过时滞镇定系统成为可能，这样的可能性也来自于Pyragas开创性地提出有意识地利用时滞状态反馈来控制混沌的思想.利用这样的理论基础，胡海岩课题组对时滞反馈控制实验进行了深入研究[40]，成功地实现了对双倒立摆所有4个平衡位置的镇定.而Ohta和Murakami[41]从相反的角度出发，通过对双摆实施控制时出现的时滞进行补偿，使得摆的稳定性得以实现.进行单摆的控制实验的还有加拿大学者Campbell课题组[4243]，他们从实验现象中验证了通过时滞反馈控制可以镇定单摆系统，而且还发现由于实验装置的缺陷，在单摆移动的过程中，单摆与滑杆之间的摩擦是黏滑运动，这种摩擦力会导致摆在平衡位置发生颤振.这些实验工作使得时滞利用方面的研究变得丰富多彩且更具实用性.

然而，迄今为止对于利用系统耦合时滞镇定、或者抑制受迫系统振动等方面的实验工作还基本处于空白.主要的瓶颈有3个方面：第一，在过去很长一段时期对利用时滞对耦合系统的动力学进行镇定的机理还不清楚，因为这种耦合系统的时滞对振子的作用较时滞反馈控制难，况且系统是非自治的；第二，如何在力学系统中实现耦合时滞是个难题；第三，如何在力学系统中实现模型研究中出现的非线性力.目前国内外的一些学者已从理论上对耦合时滞的利用机制产生了新的认识.

事实上，耦合时滞的形式可以导致无外界激励系统产生“振幅死岛”(amplitude death island).对于有外部激励的耦合系统，可以通过设计时滞吸振器来抑制振荡.Olgac等[44]首先提出将耦合的线性强迫系统与时滞耦合，可以通过在线调节时滞实现主系统的振动完全消失.这种时滞减振技术可以根据测得的外激励频率的大小调节反馈增益系数和时滞的大小，它实质上是一种主动减振技术.Olgac研究小组，经过将近3年的理论研究，获得了实现主动减振技术的理论依据，并取得了实验结果[45].但是该方法可以实现主系统振动完全消除的时滞量仅仅在一个点上，如果时滞飘移，系统的振动会更加剧烈[46].为了弥补该缺陷，Zhao等[4748]采用时滞与非线性联合耦合的办法来拓宽频带，为进一步发展和完善时滞减振技术建立了必要的基础，也为进一步开展实验研究工作提供了必要的理论依据.

目前，尽管耦合系统中存在时滞已是普遍共识，但是针对时滞耦合系统非线性动力学的研究方法还比较有限，有关如何辩识系统中时滞这一基本问题的研究工作也不多见.

综上所述，时滞效应中有动力学死区、单模态动力学行为及其转换的行为，可以用于振动抑制.然而，在很长一段时间里对于利用时滞抑制受迫系统振动等方面的实验工作基本处于空白.主要存在3个方面的问题：第一，在过去很长一段时期内未了解关于时滞对耦合系统的动力学镇定机理，因为耦合系统的时滞对振子的作用不同于时滞反馈控制，且系统是非自治的；第二，如何在力学系统中实现耦合时滞(以下称为主动时滞)是个难题；第三，如何辨识受控系统中客观存在的时滞(以下称为硬时滞)没有可以借鉴的方法.针对这些问题和难点，近几年来，一些学者在这一领域取得了以下突破：研究和建立了时滞耦合线性系统中客观存在的耦合时滞的辨识方法；构建了有非线性力耦合和时滞吸振器的实验装置，通过实验手段重点研究了主动时滞的调节机制和规律，可以通过对时滞参数的连续调节，确定使系统达到最优吸振效果的控制律与时滞区间，并通过实际测量得到的输入输出信号，探索时滞耦合非线性系统识别时滞参数的规律；设计了时滞准零刚度隔振器并用其观察无法用理论分析预测的现象；利用时滞控制设计了一种可以测量移动刚体的绝对位移的传感器.在研究中，首先面临的问题就是对于所构造的实验装置的刚度、阻尼、质量及时滞等参数的标定，以便得到时滞镇定实验的精确数据.在标定中，需要突破的是如何对时滞参数和非线性参数进行辨识.

考虑含时滞的多自由度非线性系统状态方程

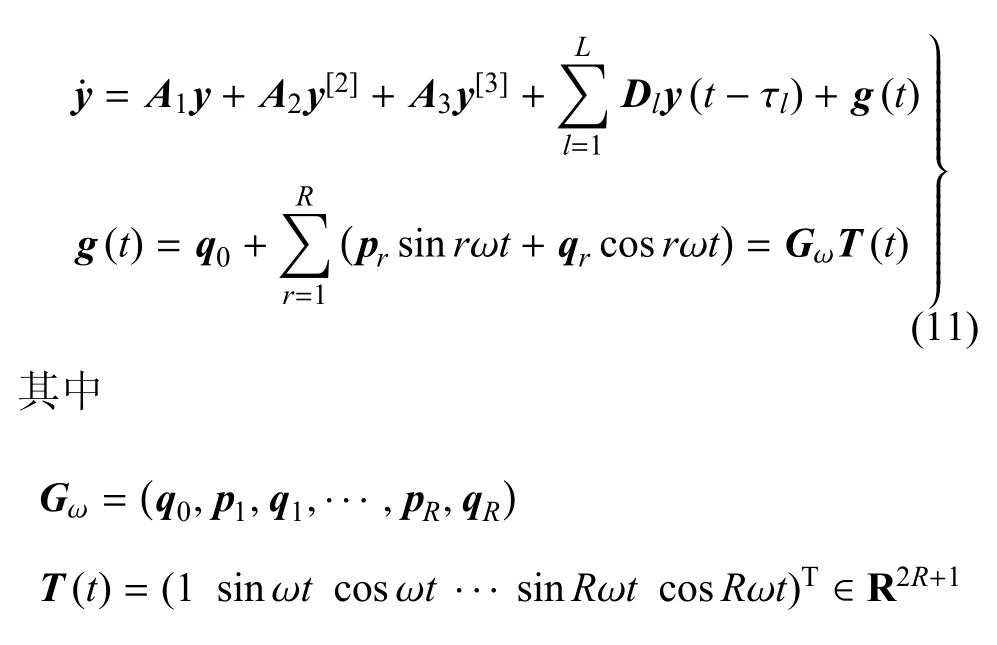
A1,A2,A3为系数矩阵，y[k]表示yk阶Kronecker积.

需要辨识的是时滞耦合参数Dl及τl.将式(11)转化为频率响应方程后，可得到关于 τl的隐式方程.由于无法直接求解，考虑引入Newton-Raphson方法[49].令则可得到迭代算法，当算法收敛时,即可辨识出时滞耦合参数.

将上述的时滞辨识方法用于时滞吸振器装置[50],如图4(a)所示，力学模型如图4(b)所示，目的是辨识系统的物理参数和反馈系统存在的硬时滞以及人工给定的控制时滞.

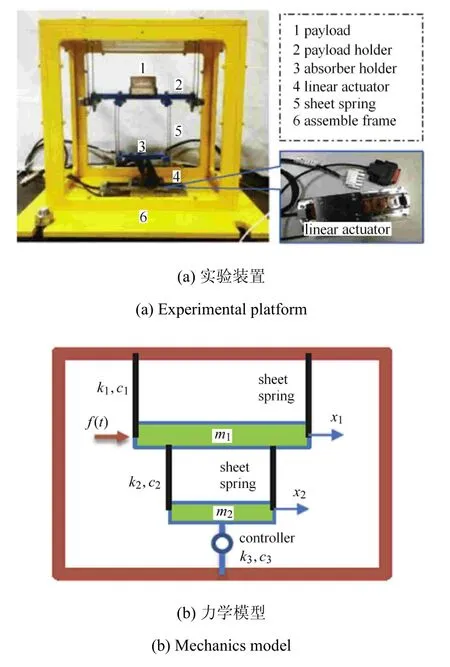
图4 时滞吸振器Fig.4 Delayed absorber

在图 4中，m1是主系统，m2是辅系统 (吸振系统)，控制器利用伺服直线电机产生反馈时滞信号g(x2(t-τ))并作动在m2上，τ是反馈时滞，数学模型为

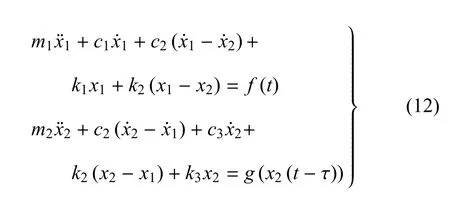
利用前文提到的辨识算法,可以得到式 (12)中的质量、阻尼、刚度和反馈环节中的硬时滞的辨识结果：m1= 0.8027kg，m2= 0.3827kg，c1=2.5238N·s/m，c2=0.4728N·s/m，c3=8.7934N·s/m，k1= 2271.2284N/m，k2= 1469.8869N/m，k3=185.6448N/m，τin=7.8920ms.

对于非线性时滞系统的参数辨识研究，Zhang等[51]构建了一个二自由度磁力非线性时滞控制实验装置，如图5所示.

图5 具有非线性磁力作用的时滞吸振器Fig.5 Delayed absorber acted by nonlinear magnetic force

图6是实测结果与辨识理论结果的比较，其中Y和Z分别对应于吸振器x1和主系统x2.可以看出，辨识的精度满足要求.

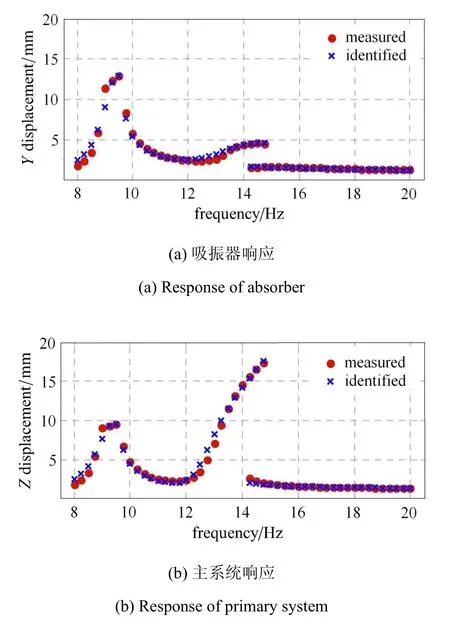
图6 辨识结果与实测比较Fig.6 Comparison between identificatio and measurement

在辨识结果的基础上，可以进一步考虑时滞吸振器吸振的效果[52].若给主质量施加正弦激励力，则耦合系统的振动对应的数学模型是

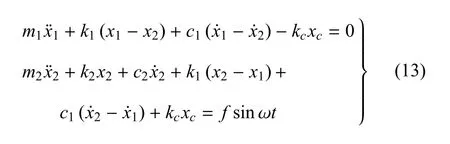
其中，kcxc表示时滞反馈控制力，kc表示作动器的刚度，xc表示反馈信号并具有以下形式xc=ax1(t-τ1),a表示反馈信号的放大系数，τ1表示固有时滞.当a≠0时，时滞反馈控制的引入将被动式动力吸振器转化为时滞动力吸振器；当a=0，时滞反馈控制消失，时滞动力吸振器退化为被动式吸振器.图7表示主动吸振器(a≠0，τ1=63ms)与被动吸振器(a=0)对主系统的吸振实验结果的比较.可以看到，耦合系统的两个共振频率分别为6.55Hz和11Hz，被动吸振器自身的固有频率为10.1Hz.当外激励频率接近10.1Hz时，被动吸振器十分有效，可以将主系统的振动降到最低.然而，当外激励频率受到扰动接近11Hz时，主系统发生第二阶共振，被动吸振器完全失效.在这种情况下，主系统的加速度传递函数值在a=-0.5和a=-1时分别降低了50%和73.4%；当Ω=10.5Hz时，主系统的加速度传递函数值在a=-1时降低了52.4%；当Ω∈[7Hz,9.5Hz]时，时滞吸振器的减振效果不明显.实验结果表明，选择合理的反馈增益系数，时滞动力吸振器可以大幅降低主系统的共振响应.

Xu和Sun[53]考虑了基于加速度信号的时滞耦合控制，其数学模型为

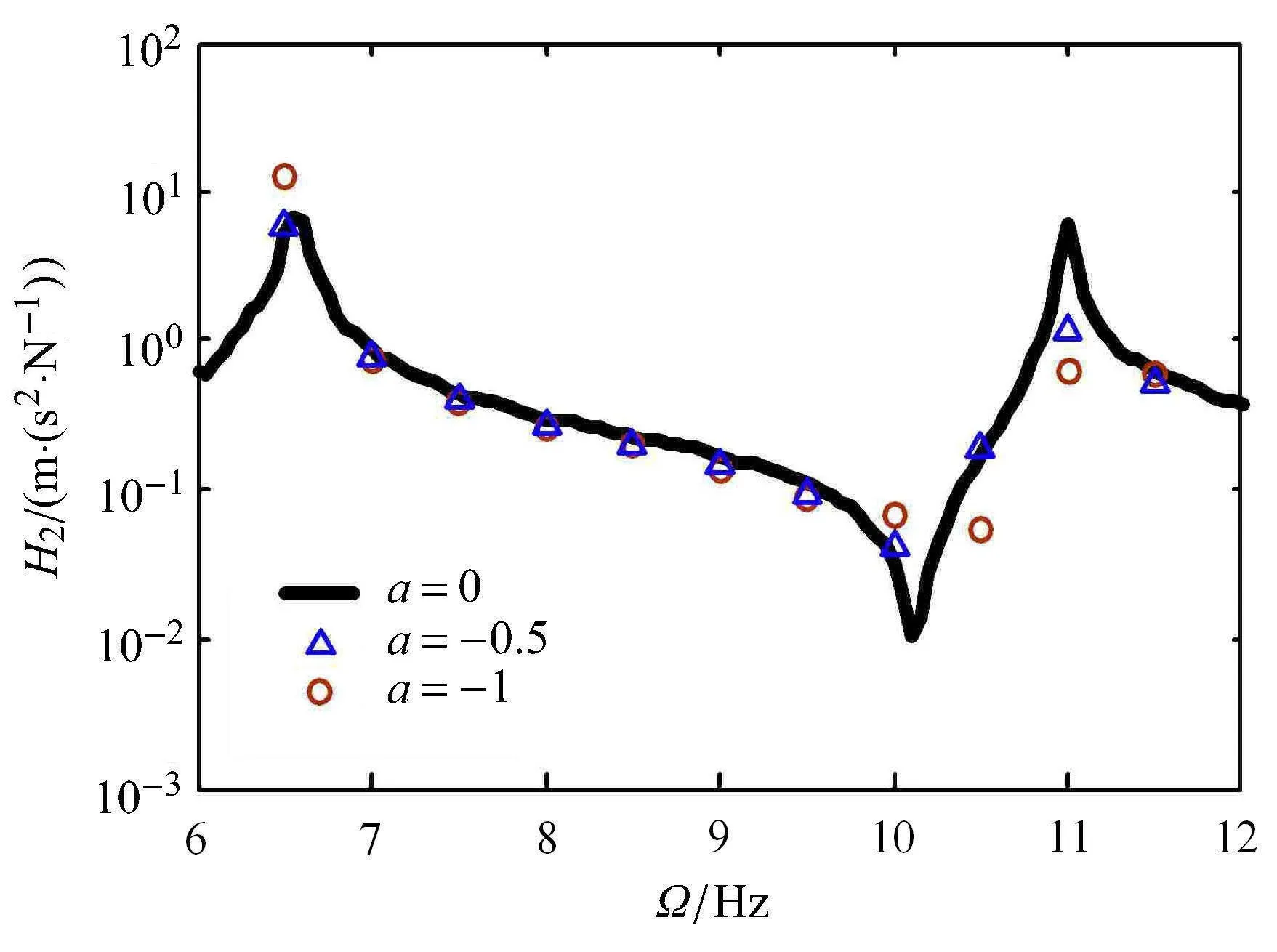
图7 时滞吸振器主结构实验测量Fig.7 Experimental measurement of primary structure in delayed absorber system

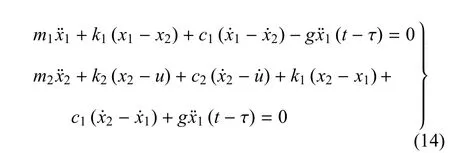
其中 u(t)表示基础激励. 记 Di= (Hi|g=0-Hi|g≠0)/Hi|g=0×100%，则可以得到如下理论判据：(1)当D1＜0，D2＞0时，时滞吸振器可以吸收主系统能量，在此频带能抑制主系统的振动，而吸振器的振幅增大；(2)当D1＞0，D2＞0时，主系统和吸振器的振幅同时减小；(3)当D1＜0，D2＜0和D1＞0，D2＜0时，时滞吸振器失效.图8展示了理论分析和实验结果的比较.

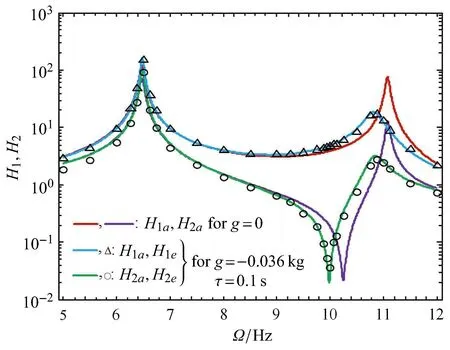
图8 理论分析和实验结果的比较Fig.8 Comparison between theoretical analysis and experiments

从图 8中看出：(1)当 Ω ∈[8Hz,10.0625Hz](D1＜0,D2＞0)时主系统和时滞吸振器之间发生能量转移.具体表现为主系统的振幅减小，而吸振器的振幅增大.值得注意的是，当Ω=10Hz时主系统的振幅降低了80.03%，而吸振器的振幅增大了22.19%；(2)当 Ω ∈[11Hz,12Hz](D1＞0,D2＞0)时，主系统和吸振器的振幅均有不同程度的降低.特别是当Ω=11.125Hz时主系统和吸振器的振幅分别降低了73.19%和79.79%；(3)由于引入时滞反馈后反共振频率减小，当Ω=10.25Hz(D1＞0，D2＜0)时主系统的振幅骤增了597.58%.然而可通过时滞耦合强度g和时滞τ的调节实现对主系统的吸振，如图9所示.从图9可以看出，只要选取合适的主动时滞和反馈增益便可有效调节反共振点的位置，且按照上文给定的判据就可实现时滞吸振器的有效吸振.

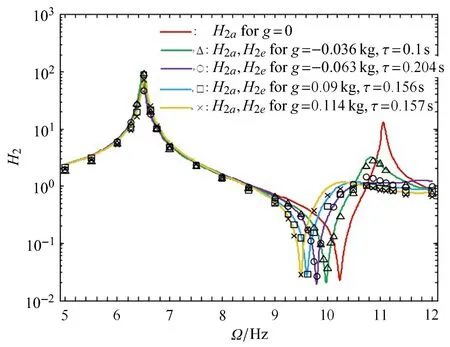
图9 通过调节g和τ拓宽主系统吸振频率Fig.9 Modifying gand τ to extend frequency band of vibration absorption for primary system

近年来，学术界对“准零刚度隔振器”进行了广泛研究，通过调节准零刚度隔振装置水平弹簧的预压程度，可以降低结构的共振频率，从而拓宽有效隔振频带.然而，准零刚度隔振装置存在一些缺陷，首先，当水平弹簧的预压增大时，结构的线性刚度被减小，但是当结构的线性刚度小于零时，结构会失去静态稳定性，容易出现失效、塌陷等现象；其次，虽然通过减小线性刚度的方法拓宽了结构的隔振频带，但是共振峰值并不能减小；最后，利用水平预压弹簧形成的准零刚度隔振结构，当其线性刚度减小时，非线性刚度系数增大，因此会形成较大范围内的多稳态现象.Sun等[5455]利用时滞主动控制装置研究准零刚度隔振结构的特性，并且讨论了时滞主动控制对结构的稳定性的影响，探讨不同激励模式下准零刚度隔振装置隔振效果的改进程度和机理,如图10所示.

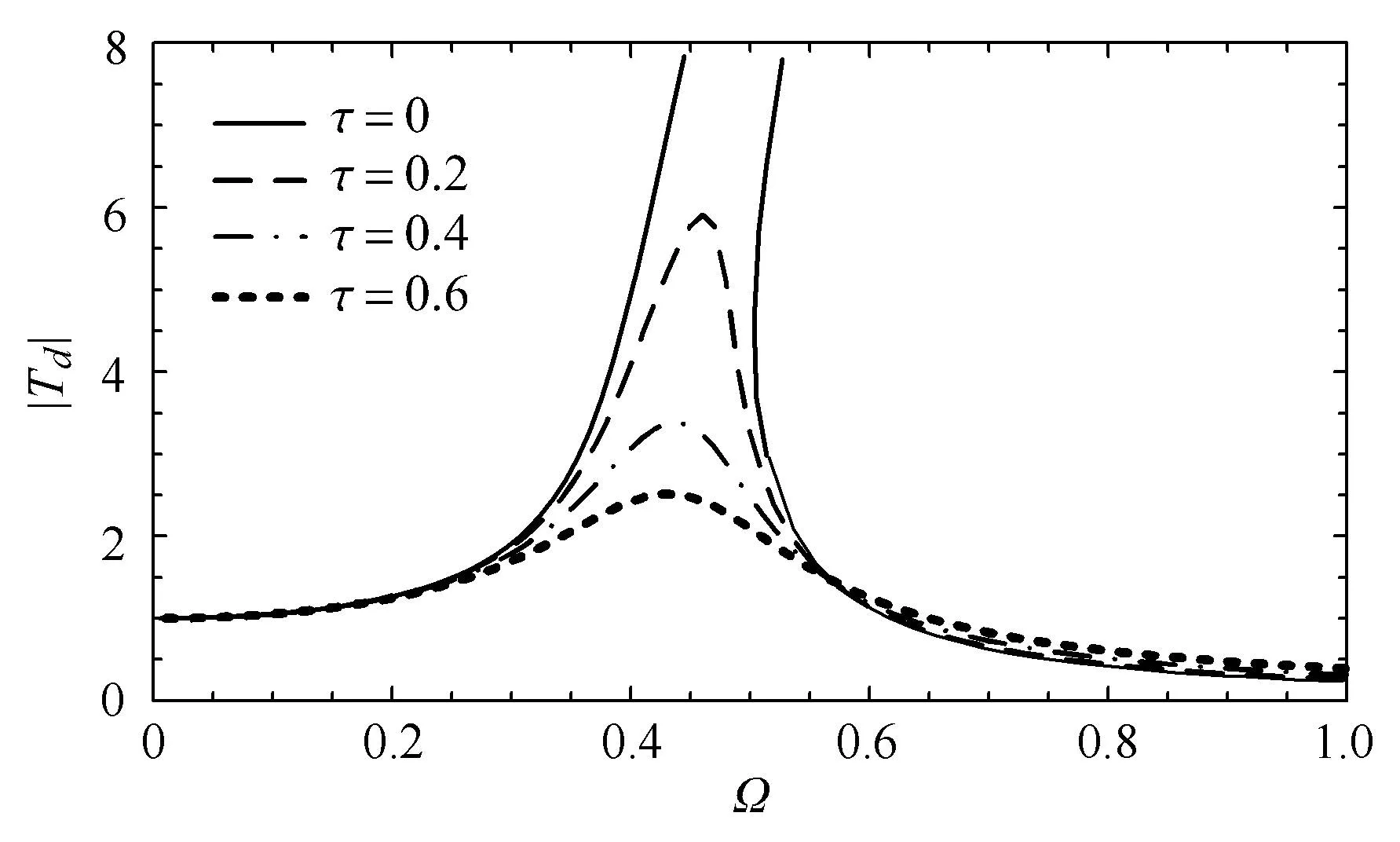
图10 时滞耦合控制降低失效隔振区振幅Fig.10 Delayed control to decrease the amplitude at failed band for isolation

针对测量振动物体绝对位移的需求，Sun等[56]研究和设计了一种测量振动物体绝对位移的测量装置，基于准零刚度的隔振结构可以作为传感器来测量振动物体的绝对位移和绝对速度.传感器的结构如图11所示，其中绝对位移传感器的结构部分基于前文中提到的准零刚度隔振结构.从图11可以看出，传感器部分由一个较小的质量块、两根水平弹簧和一根竖直弹簧组成.竖直弹簧和基座中装有力传感器，用于测量竖直弹簧的弹性恢复力，以此可以得到传感器质量M2和被测物体M1之间的相对位移.而由于M2的振动基本被隔离，因此M2和M1之间的相对位移与M1的绝对位移非常接近.类似的剪刀型装置可以实现对多个方向绝对运动状态的测量，也可以把测量得到的振动物体的绝对位移直接作为主动控制信号源使用，从而改进了多方向振动物体的振动控制效果[57].

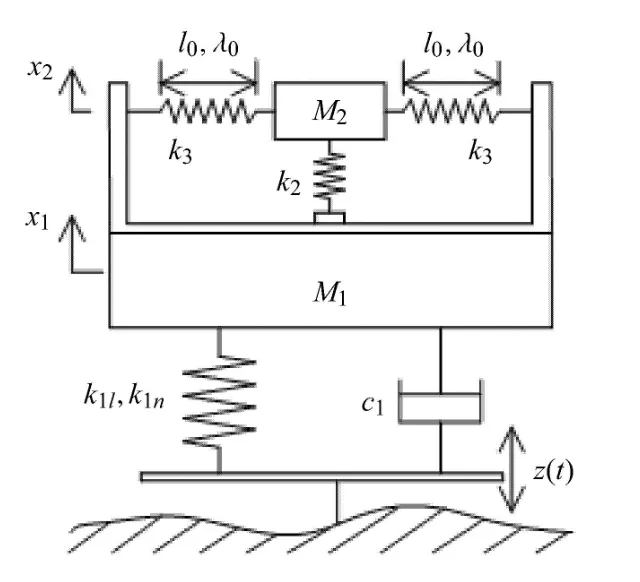
图11 测量移动物体绝对位移装置Fig.11 Device to measure the absolute displacement of moving body

非光滑系统在现实中广泛存在，有一种具有阶跃形式的时滞耦合系统便属于非光滑系统，这种阶跃形式常常用Sigmoid函数进行建模，由于这种模型是一种简化的近似形式，Sigmoid函数中的坡度因子(slope ratio)的确定就显得尤为重要，即需要明确坡度因子对时滞耦合系统时滞镇定的作用是否具有本质的影响.研究结果表明，这个因子在时滞耦合系统中，可以诱发从周期运动-概周期运动-混沌这样一个转迁过程，并且随着坡度因子的增大，系统从混沌模式转迁至多周期运动状态，然后又通过倍周期分岔进入混沌区域，并且时滞可以诱发多稳态解[58].研究结果也表明，在对非光滑系统进行光滑近似处理时要尤为谨慎，这也说明利用工程中使用的限位器镇定系统需要更加精细的设计，在这类问题中镇定开关的功能不易实现.这也为研究利用时滞耦合抑制系统的振动提供了研究动机和理论依据.

自参数振动是一种特殊的非线性振动，饱和现象是非线性自参数振动系统一种重要的特征.在弱非线性振动系统中，当一个两自由度的系统固有频率比为1：2，并且高阶模态受到主共振类型的外激励时，系统就会出现饱和现象.利用非线性自参数振动系统的内共振产生的饱和现象能够实现对主振动系统的宽频带控制.由于饱和控制时主振动系统存在一定的振幅，对于对振动控制要求不高的控制系统而言，饱和控制能够达到系统对振动控制的要求；然而，对于一些精密仪器设备的减振需求，饱和控制的减振效果并不理想，主振动系统的振幅则需要进一步加以控制.针对这一问题，Zhao等[5960]采用时滞反馈控制来控制自参数振动系统饱和控制时的振幅，通过研究一个带有参数激励摆的两自由度质量弹簧振动系统的振动控制问题.当主系统质量块受到简谐激励作用时，在辅系统单摆上施加一个具有时间滞后的反馈控制.研究结果表明，反馈增益系数和时滞是两个可以独立调节的控制参数，当反馈增益系数和时滞在某个范围进行调节时，能够减小主振动系统的振动.当反馈增益系数和时滞都调节到某个特定的数值时，主系统的振动几乎可以完全消除，达到了理想的抑振效果.通过时滞耦合的时滞主动控制，实现发生1：2内共振时的参数吸振模式，从而达到吸收主系统的振动能量以抑制主系统振动的目的，结果表明合适的时滞主动控制，可以抑制主系统的振幅达到56%，为进一步探索理论上的机制和实验验证提供了必要的基础.

时滞抑制振动的技术也被应用于磨削过程的再生颤振抑制和网络拥塞控制中.在磨削过程中时滞来源于前一圈磨削的时间，因此利用时滞控制就是控制转速，那么问题便可以描述为在不降低转速的前提下如何抑制再生颤振.Yan等[61]通过在原有转速基础上施加微小的变速，实现了对颤振的抑制，并通过理论分析与数值模拟明确了转速参数与颤振抑制效果的关系.在网络拥塞控制问题中，时滞(即回环时间)是一个不可忽视的参数，已有的研究表明，网络中的振荡可能与时滞有关，而振荡将会提高网络拥塞的可能，不难理解，时滞诱发的振荡(特别是同步振荡)将会增加网络系统出现拥塞的可能性或使已出现的拥塞进一步恶化.Zhang等[62]提出将时滞作为一个控制参数，当发现网络中出现振荡时，对时滞施加一个小的周期摄动，可以起到镇定系统的作用.这为设计新的控制策略提供了理论依据.另外，网络是典型的时滞耦合高维非线性系统.Zhang等[63]考虑了n维Kelly型拥塞控制模型，假定n个用户共享同一条链路，但各个用户的物理参数可以不同.他们以时滞为分岔参数，求得系统平衡点失稳后产生的振幅-频率方程和周期解，从而明确了高维拥塞控制问题中时滞和由其所诱发的发包速率周期振荡之间的定量关系.为了抑制振荡，对各个用户的时滞施加频率相同的小幅周期摄动，利用直接求解振幅--频率方程和快慢变系统理论这两种方法，得到镇定系统所需的时滞摄动参数应满足的条件.值得注意的是，在多用户的网络系统中，可以只对其中一个用户的时滞进行摄动而达到镇定系统的目的，这在理论上为基于周期时滞的网络振荡控制器的设计提供了可行性.另外，对一个已经引起周期振荡的时滞进行周期摄动，当摄动的幅度超过阈值时，系统的振荡将会得到抑制.通过时滞多尺度方法可以从理论上计算出该阈值的大小.这意味着通过这种手段也能有效降低因振荡引起网络拥塞的风险[64].此外，较大的时滞可使网络出现周期振荡，而较大的传输距离和较小的链路容量也可能是引起用户发包速率出现振荡的原因.针对环形网络，Zhang等[65]提出环形网络的拓扑结构单参数的表征方法，给出了跳数、时滞与环形网络的振荡之间的关系，从而揭示了环形网络中较大的跳数使得发包速率出现振荡的现象.然而，在进行上述时滞主动控制技术的应用中，一定要注意网络的拓扑结构，即使在一个拓扑结构简单的网络系统中，各种时滞如多时滞、状态依赖时滞等也可以诱发复杂的动力学行为[6668].

对不同的问题，控制设计不仅要保证受控系统稳定，还要具有一定的性能，如能耗最少、收敛速度最快等.此时可采用最优控制理论.由于输入时滞在控制系统中是普遍存在的，这使得控制器不仅要利用当前状态，还要利用过去的状态，这给控制设计带来了很大的困难.传统的做法是先将含输入时滞的控制系统转化为无时滞的控制系统，然后利用无时滞控制系统设计出满足无时滞系统的性能指标最优的控制器.这样带来的问题是：控制性能指标不是基于原系统而是转化后的系统，反馈控制器不是由原系统的状态变量表示的，而是转化后的系统状态变量.为了克服这一困难，Zhou等[69]研究了具有输入时滞的最优控制设计问题，发现了原系统的反馈控制和转化后系统的反馈控制之间的数量相等关系，进而可设计出基于原系统性能指标下的反馈控制，且控制由原系统的状态变量表示.由此设计出的反馈增益比无时滞时的控制增益小，由此说明时滞可看作有利的因素.数值算例验证了控制设计方法的可行性和优越性.另外，如何通过反馈控制器的作用来镇定不稳定的时滞网络或者改善网络的稳定性是一个重要的问题.朱霖河等[70]研究了一类受控二阶惯性神经网络系统的稳定性和分岔，通过数值实验说明如何选择参数和时滞使系统收敛速度不断加快、延迟网络的分岔发生且扩大稳定域等问题.

综上所述，为了深入认识时滞积极的作用并进行技术实现，有必要开展研究并建立时滞耦合系统中客观存在的耦合时滞的辨识方法，特别是研究周期振子通过时滞状态耦合后，时滞和耦合强度是导致耦合系统从动态走向平衡态的参数条件，构建和实现时滞和非线性对目标耦合系统的实验平台并进行实验.

3 快慢变时滞耦合系统动力学

在对实际工程和生物系统的研究过程中，已经发现有一大类的耦合系统是所谓的快慢变耦合系统[71].如果这样的耦合过程考虑时滞，就是快慢变时滞耦合系统.这类系统的特点是耦合子系统个体的变化速度有量级的差别，耦合后系统表现的状态是快变和慢变交替出现.快慢变系统是典型的奇异摄动系统，这种系统中含有不同的动力学时间尺度，其最典型的运动是脉冲形式的振荡解和簇动形式解.例如输电线力场和流场的耦合产生所谓的张弛运动、细胞生物学中表现出的尖峰等都是快变和慢变量耦合的结果.这类系统的派生系统是泛函微分--代数系统，所以理论研究具有很大的挑战性,其研究难点是如何求得系统中的快变流形和慢变流形.

近年，对低维的快慢变常微分系统的研究已有一些结果.例如假设捕食者变化相对于被捕食者较慢，England等[72]发现这样的快慢变系统失去平衡且有滞后的现象.Wiggins的研究小组[73]进一步给出了针对一类三维快慢变时变系统计算其快慢变流形的方法，可以计算余维1(不变)稳定和不稳定流形.对于机械系统，如果在耦合的力学系统中的某个子系统呈现强非线性特性，则该子系统就会表现出快变特征而与耦合系统中其他的子系统进行能量交换，并显示出快速和慢速交替的交换态势[74].特别是结构出现非对称的时候，也会存在类似的能量交换态势.如果是通过周期运动交换，则会表现出类似生物系统的尖峰振荡[75].这种能量的传递形式在工程控制中更加普遍，特别是对于控制器本身通过非线性结构实现的情形[7677].

目前对含时滞的快慢变系统关注得较多的是系统的稳态运动特征，但对系统如何由暂态过程进入稳态过程这方面的工作还不多见.南京航空航天大学王在华教授课题组在这方面做了大量的前期研究工作：通过研究一类具有快慢变TCP/AQM时滞网络模型，发现当时滞较小时，系统处于稳定状态；且只有当时滞为适当大小时，系统才能达到最佳的稳定状态.这与通常认为时滞越小越好的想法不一致.当时滞超过临界值时，系统的平衡点将失去稳定性，系统发生Hopf分岔产生周期运动[78].特别是在快慢变耦合时滞系统中同样存在着分岔滞后现象[79],时滞对逃逸值有重要的影响.在机械系统领域，Jiang和 Xu[80]将机械臂的柔性关节考虑为如图12所示的力学模型.

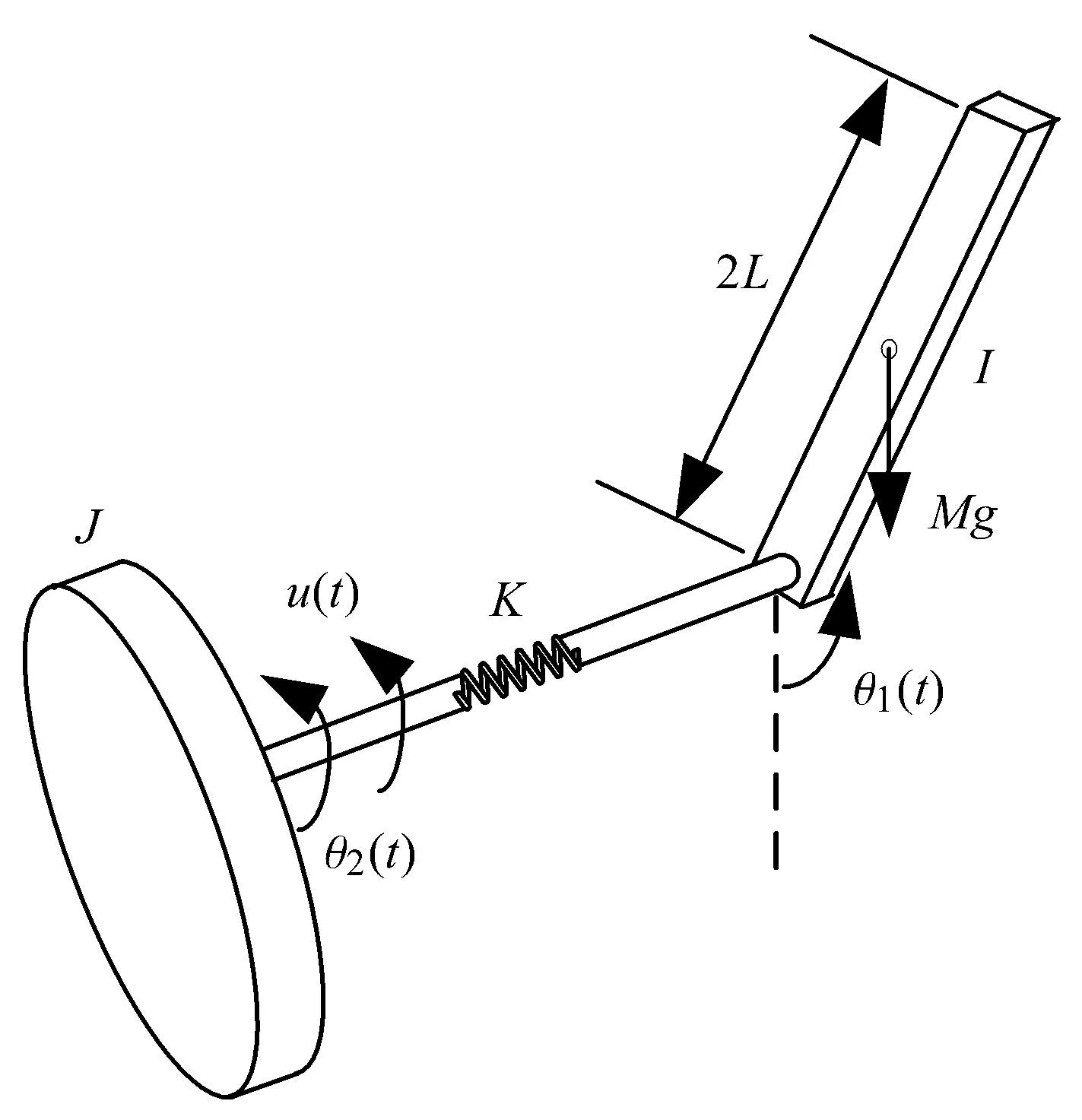
图12 柔性关节机械臂Fig.12 Robot arm with fl xible joint

在一个刚性连接件--弹性关节系统(the rigid-link fl xible-joint system)中，驱动转子和连接件通过一根细长的弹性轴连接，转子和连接件分别是两个刚体.将连接关节等效为一个线性扭转弹簧，其扭转刚度为K.记刚性连接件和驱动转子的绕弹性轴中心线转动的转动惯量分别为I和 J，转动角位移分别为θ1(t)和θ2(t).在实际工程中，关节部分有各种各样的齿轮减速器装置，由于减速器的齿轮存在间隙，则驱动和作动臂动作会相差一个时滞，记为τ，这个时滞就是模型减速器中齿轮间隙和作动的时间，通过将传递时滞引入现有的机械臂模型，可以得到弹性关节系统控制方程

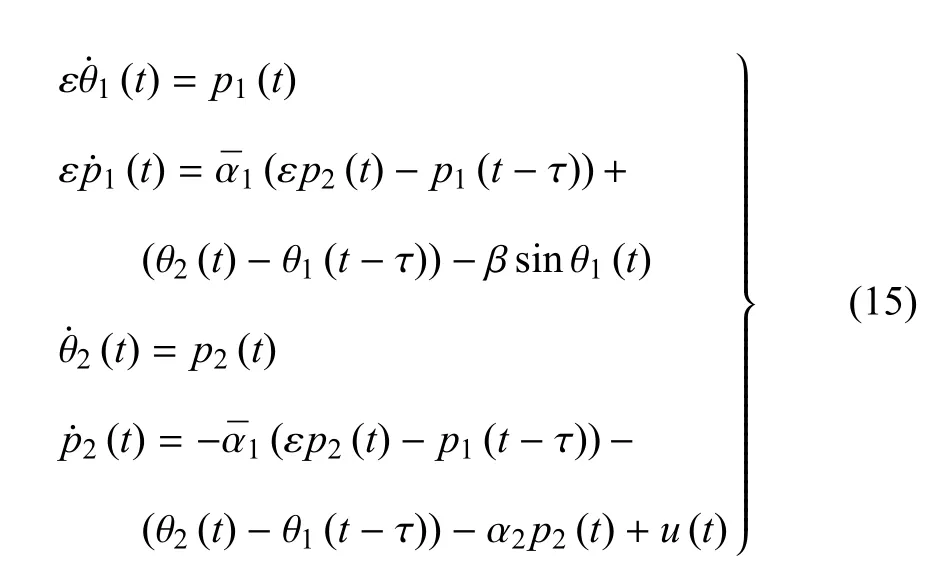
这是一个典型的具有耦合时滞的快慢变系统，其中ε≪1,u(t)=aθ1(t)+b是驱动.慢变流形和快变流形分别为

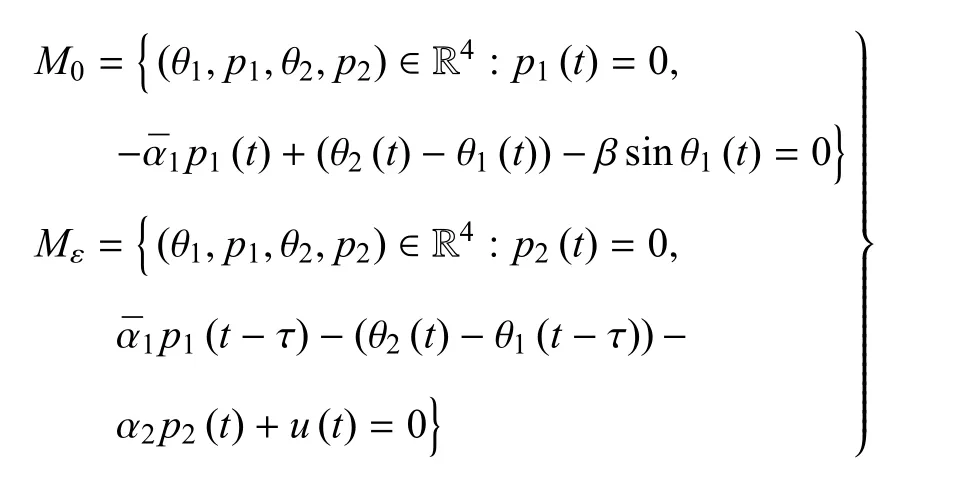
快变流形与慢变流形相交的形式决定了系统的动力学行为，而快变流形又被控制的形式u(t)决定，如果控制形式不恰当，对应的系统动力学行为会分别表现出尖峰和簇,如图13所示，从而影响机械臂到达目标精度[81].

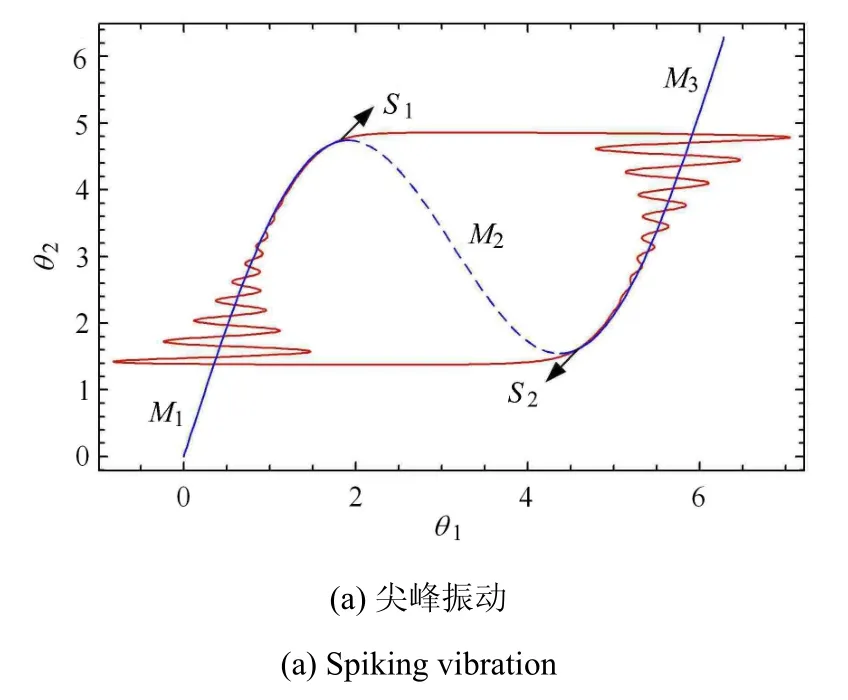
图13 系统(15)在不同驱动下的振动Fig.13 Vibration of system(15)subjected to distinct drives

经典的 Van der Pol振子是一个典型的具有快慢变量的动力系统，表现为一种简单形式的张弛振荡，有着重要的应用背景.郑远广等[82]详细分析了反馈时滞对Van der Pol振子张弛振荡的影响，通过稳定性切换分析和几何奇异摄动理论，发现时滞反馈会引起张弛振荡中的慢速运动过程中存在微幅振荡，其中微幅振荡来自于内部层引起的振荡和Hopf分岔产生的振荡两个方面；同时时滞对张弛振荡的周期也具有显著的影响，当时滞增加到一定程度时，慢变过程中的微幅振荡消失，系统出现方波形运动.

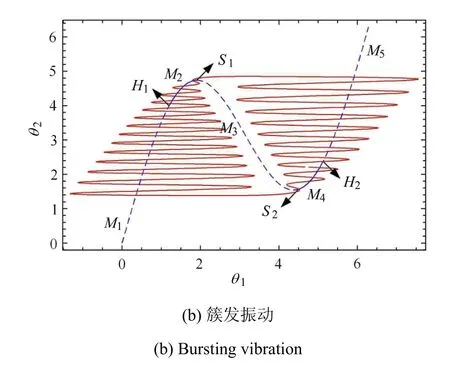
图13 系统(15)在不同驱动下的振动(续)Fig.13 Vibration of system(15)subjected to distinct drives(continued)

为了方便理论分析，文献中通常假设时滞是时不变的.但实际上，很多实际问题中出现的时滞是慢时变的，为此，Zheng等[83]考虑了时滞为慢时变函数的情形，研究发现如果慢变时滞是周期函数，则分岔点也周期性出现.利用特征函数在分岔点附近的实部函数可以计算出逃逸函数的近似表达式.如果该函数在某些区间上无零点，即无逃逸点，则原时滞微分方程在常时滞情形已失稳的解在周期慢变时滞情形是渐近稳定的，从而解的稳定性得到改善，而Hopf分岔会延迟发生.时变时滞在多数情况下被认为是不利的因素，不仅导致复杂的动力学，也会使分析与计算更加复杂，而上述结果表明，恰当选择慢时变周期函数时滞可延迟分岔发生，改善稳定性，因而时滞可被认为是有利因素.

不同神经元变化的时间尺度可不同，此时系统呈现出典型的快慢变量耦合系统的动力学特征.Zheng等[84]应用几何奇异摄动方法，研究了两神经元Hopfiel模型的非线性动力学，得到了系统产生张弛振荡的条件以及张弛振荡周期的估计式，进而研究了时滞对平衡点的吸引域的影响.进一步的，Zheng等[85]还得到了处于同步之后的耦合神经元的Hindmarsh-Rose模型的簇放电模式与耦合时滞对簇放电模型的影响，以及由簇放电到混沌的转迁模式与机理.

综上所述，快慢变耦合时滞系统与时滞的关系有着特殊的规律性，有必要开展研究工作，特别是针对快慢变耦合时滞系统与不变流形方法有关的新方法，耦合时滞对状态变量在不同时间尺度下快、慢变量的影响规律，探讨时滞对快慢变系统张弛振动和能量转化的影响规律，进而研究多稳态运动的形成等复杂动力学行为产生的机制.

4 时滞神经网络同步和去同步

时滞神经网络不但是系统生物学重要的研究内容之一，也被广泛用于人工智能控制、快速算法等应用领域，并且已经逐步涉及到以网络为基础的科学和社会活动，研究领域包括智能控制、细胞与新陈代谢网络、神经网络、电力网络、人际交往网络等.一方面，网络系统表现出的行为常常需要协同性，即同步现象；另一方面，在系统生物学研究领域，很多疾病的表现特征是某种动力学行为的同步.例如在帕金森病理条件下，某些神经元同步放电，导致运动前区和运动皮层的同步活动[86],这样就产生了同步问题的反问题——去同步(desynchronization).因此，同步和去同步是耦合时滞神经网络群体动力学的两大表现形式，也是时滞神经网络的核心研究方向.同步状态主要有完全同步、相同步、延迟同步、广义同步、间歇延迟同步以及不完全相同步(imperfect phase synchronization).

近年来，报道同步的研究成果的文献超过上千篇.有如此多的文献来探讨同步问题是因为可以使用的基本数学工具非常有限.一般采用将原系统变换成误差系统，利用Lyapunov方法研究出现同步的充分条件.由于在充分条件以外总能找到新的同步参数范围，导致大批学者都在寻找更加接近必要条件的参数范围.这些由常微分方程组或图表示的系统具有规则的拓扑结构和系统机制简单的特点，人们可将研究重点放在由节点的非线性动力学性质引起的复杂性上，而不需考虑网络结构的复杂性.但是，信号在网络节点间的传输速度、节点间的相互作用或生物网络中个体的生理特性等都会引起时滞.因此，网络实际上是一个高维时滞动力学系统.近年来，随着生物、信息和数学等学科的发展，时滞对复杂网络的重要影响已逐渐被认识.然而，对于时滞神经网络系统的同步研究，由于需要寻找时滞依赖的充分条件，因此必须推广Lyapunov方法，目前主要采用的方法有Lyapunov-Krasovskii方法[87]、非线性观测法[88]和线性矩阵不等式法[89].另外，有一些学者也开始关注异构时滞神经网络的同步问题.事实上，从自然和工程角度出发，保持子系统完全一致的耦合神经网络不存在，因此，研究异构时滞神经网络的同步问题更具有科学和工程意义，同时也更具有挑战性.在这方面，中国学者陆启韶教授领导的课题组做了大量的工作，他们主要是采取数值仿真的方法[90].通过理论分析的方法，Li等[91]和Huang等[92]分别研究了更加一般的耦合网络和异构的时滞神经网络的同步和混沌同步.值得注意的是大部分的理论分析方法还是采用了寻找同步的充分条件，但是该充分条件已与时滞有关.最近，Song等[9394]利用时滞微分方程的等变分岔理论，研究了Hopfiel型时滞耦合神经网络模型在双向耦合时，时滞会导致同步开关现象，即在耦合强度与子系统的内在参数组成的参数空间的一定区域内随着时滞的增大同相同步和反相同步会交叉出现.在单向耦合时，没有这种同步开关现象出现，但时滞仍会导致同相同步和反相同步现象，在耦合强度与子系统的内在参数组成的参数空间的一定区域内，Hopf分岔产生的周期振动的振动模式不依赖于时滞.在这两种情况下，耦合强度对Hopf分岔产生的周期振动的振动模式具有类似的影响，即在兴奋性耦合下是同步振动而在抑制性耦合下是反相振动.然而，这些研究工作考虑的都是两个完全相同的Hopfiel型系统具有时滞耦合的情形，对于更普遍的系统和多个子系统的情形，网络结构和耦合时滞对同步模式的影响规律还不清楚.

作为同步活动的反问题，近来由于实际问题的需要，尤其是神经科学方面的应用，在欧美尤其是德国许多学者开始关注去同步策略的研究.德国学者Tass[95]最先应用非线性动力学和统计物理的方法研究去同步策略，并提出多种脉冲序列去同步的方法[96].目前去同步技术大致有[97]周期激励和非周期刺激法、脉冲序列去同步技术、线性和非线性时滞反馈以及Washout滤波反射法[98]等.异常有害的同步活动并非仅限于神经系统.力学中最典型的例子是伦敦千禧桥，在其首次开放日活动上，由于众多行人同步的步态，导致千禧桥大幅度的左右晃动[99100].因此，去同步的研究具有广泛的物理意义.但总体上相对于同步而言去同步的研究还处于初期阶段，国内对于去同步的研究则更少，尤其对时滞耦合神经网络的去同步机理还不清楚.

总之，如何对复杂网络进行精确的科学描述和对网络配制进行优化；如何建立一套适应大规模网络计算环境的理论和模型；特别是如何利用这些成果并从网络系统的观点出发，研究时滞耦合的力学系统等都是值得关注的科学问题.同时，利用动力学分析网络环境系统的去同步也是一个基本问题，是以往非线性动力学尚未遇到的新问题.

如前所述，大部分研究都是在Lyapunov方法基础上寻找同步的充分条件，不同于这些研究的研究思路，一些学者开始寻找特定条件下同步的充要条件，并力争给出解析的判据.在去同步方面，主要是针对具体问题进行应用研究.下面对这方面的研究成果进行具体介绍.

同步是自然界中的一种基本现象，它普遍存在于物理、生物、化学等诸多领域中.如马来西亚岛上成千上万只萤火虫在夜晚同步闪动.对于激光的相干输出，只有当各激光器通过耦合达到同步状态时，才可以得到高功率的相干输出.但是在异常情况下，同步会导致巨大灾害，例如伦敦的千禧桥.而许多神经系统疾病如帕金森氏症，原发性震颤和癫痫等，都是由于某些脑区域异常同步放电所致.因此，研究同步和去同步方法具有广泛的意义.目前大部分时滞耦合同步的研究都是采用Lyapunov稳定性理论，然而，当不能构造Lyapunov函数时，就无法研究同步，对于去同步的研究工作就更少.由于同步问题越来越开始走向应用，因此，各种同步态和非同步态的理论研究方法的需求也在日益增加.

针对如何判断同步与非同步，Wong等[101]通过构造辅助系统的方法，即对存在平衡态的耦合系统，构造一个辅助系统，就可以得到一种判断耦合系统广义同步的解析判据，这个判据的特点在于规避了通过寻找Lyapunov函数的方法对系统是否可以达到广义同步进行判断，能有效估计强广义同步的门槛值，并且其精度与通过Lyapunov函数方法得到的结果相同.通过该方法的应用，作者得到了一个重要结论：耦合系统的平衡态越多，广义同步的机会越大，但是越不易出现强广义同步.在上述广义同步的解析判据基础上，Wang等[102]又提出了“投影系统方法”，并成功地将此方法应用于判断耦合混沌系统的修正投影同步.该方法的特点同样在于不需要寻找Lyapunov函数就可以得到判断混沌系统同步的充要条件.

系统的耦合时滞可诱发周期运动，并且耦合时滞可以引起系统的进一步变化，然而对各种运动的形成机制还并不明确.Song等[103104]提出了理论上的判据来判断同相位周期运动和反相位同步运动，结果表明仅仅通过逐步增加耦合时滞便可实现在同相同步和反相同步之间的切换，这对于连续体的控制有重要的意义，说明可以通过主动时滞控制完成模态之间的切换.更进一步，Song等[105]研究了耦合时滞对系统同步模式的影响.通过计算中心流形和规范形并应用时滞系统的等变分岔理论，得到了耦合时滞诱发同步转迁的临界值.在两振子耦合Van der Pol系统中，随着耦合时滞的增大，系统会在稳定的同相同步、振幅消亡、反相同步之间切换；在三振子耦合Van der Pol系统中，随着耦合时滞的增大，系统会在稳定的锁相同步与振幅消亡之间切换，与两个稳定的锁相同步相伴的还同时有3个不稳定的镜面反射波和3个不稳定的驻波.研究结果表明，时滞可以诱发同步态不同形式的切换，也可诱发同步与非同步之间的转迁.此外，应用前面提到的摄动-增量法也可以得到同步周期解的判据[106].这种周期振荡同步在工程中也有需求[107]：当多个振荡系统相互耦合时，耦合过程中的时滞会影响系统的稳定性、同步形式以及振动响应，研究发现高维的振荡系统不同形式的同步解依赖于时滞的取值，利用给出的周期振荡同步的判据，可以利用时滞来实现不同运动状态之间的切换.Wang等[108]研究了两个带有反应扩散项的环状神经网络的同步态稳定性和Hopf分岔问题.将时滞τ作为分岔参数，利用偏泛函微分方程的稳定性和分岔理论，分别讨论了系统各自的同步态动力学行为，给出了同步态稳定性与Hopf分岔的判别条件.研究结果分别揭示了时滞τ，耦合强度c以及扩散项对系统的影响：(1)处在耦合环状神经网络不同位置的时滞τ发挥不同的作用，既可以加快系统同步的速度，也可以减慢系统同步的速度；(2)扩散可以加快系统同步的速度，使同步态系统的平衡点稳定；(3)随着耦合强度的增长，系统同步的速度也会加快；(4)可出现复杂的多稳态共存现象.

在去同步的研究方面，Luo和Xu[109]应用辅助反馈技术，研究讨论了两个耦合Rossler振子群的同步现象，研究在主动--主动系统(即两个振子群在解耦条件下自身同步，它们之间的相互耦合导致两个群之间的同步)以及主动--被动系统(在解耦的情况下，一个振子群同步，而另外一个振子群非同步，但它们的相互耦合作用不仅导致被动系统内部同步，而且导致主动系统与被动系统之间的相互同步)中系统参数(尤其是频率分布)对于系统同步的影响，发现耦合振子群的“振幅死亡”，即振子群之间的相互作用导致各个耦合振子群去同步.随后他们应用Washout filte辅助反馈方法研究了耦合振子群去同步策略.对于主动--主动系统，探讨了控制一个群和同时控制两个群的策略；而对于主动--被动系统，研究了分别控制主动、被动和同时控制两个振子群的策略.研究发现，控制所有的振子群能有效阻止耦合振子群的同步.而局部控制，即控制一个振子群只能抑制受控振子群的同步，然而另外一个振子群仍然保持同步状态，无论它原先是主动系统(解耦条件下是同步的)抑或是被动系统(解耦条件下是非同步的).但是从另外一方面而言，受控系统的去同步状态不受其他耦合系统的影响.

5 结论与展望

本文以工程系统精细化和智能化发展要求以及时滞系统动力学理论发展需求为驱动，对以时滞为中心的耦合系统复杂动力学机制、时滞镇定耦合系统的实验基础和实现、快慢变时滞耦合系统动力学奇异性和时滞神经网络同步和去同步4个方面的研究进行了综述，介绍了近期取得的一些研究进展和成果.在研究方法方面，展示了研究时滞耦合系统非共振和共振分岔(高余维)及其分类方法、研究时滞振动系统周期运动的积分迭代法、基于Maple软件环境下的符号计算方法、具有鲁棒性的时滞辨识算法、有别于Lyapunov方法判断耦合系统广义同步的新解析判据和周期解正向同步和反向同步解时滞临界值的解析判据.在应用方面，综述了利用时滞和非线性对振动系统进行吸振和隔振的学术思想以及相应的设计和实验结果，展示了快慢变时滞耦合弹性关节系统多种复杂振荡的产生机理.

值得指出的是，本文还有许多方面没有涉及，例如时滞系统非线性动力学的稳定性和鲁棒性问题、中立性系统的动力学以及时滞耦合系统的复杂运动等.在本文涉及的研究中，下面的问题也是值得考虑的.

5.1 时滞系统动力学的一般性理论与方法

(1)时滞非线性振动系统的辨识方法

无论是从事科学研究的实验验证，还是针对现实存在的非线性时滞振动系统，都有必要对系统中存在的时滞及非线性参数进行辨识和测量，而要实现这一目标，其挑战在于：第一，在机械结构大型化及智能化的趋势下，具有不同功能的部件不再相互独立，而是一种高自由度、强耦合的复杂整体.在系统状态监控中，由于测点的分布规则仍然缺乏科学的指导，这就导致实测的动力学信息往往是非完备的，即使对于线性系统，其参数的可辨识性也变得难以论证，而构造相应辨识算法的难度也可见一斑.第二，当结构的响应幅度较大时，其动力学特性往往会表现出显著的非线性，因此原本适用于线性系统的信号分析手段(如：相关函数、传递函数等)不再适用；此外，参数辨识算法往往是基于动力学分析所得的频响函数构造的，而非线性动力学分析方法在处理高自由度、强非线性问题上还不够成熟.因此，如何处理非线性响应数据，并由所得数据构造相应的辨识算法，仍是参数辨识领域尚未解决的难题.第三，激励源与激励对象装配后即构成耦合整体，这将导致结构所受的激励产生幅值或频率上的畸变，从而打破理想激励条件.尤其当载荷方向与结构振动方向不一致时，载荷与系统耦合为参激系统，此时载荷的形式甚至决定了系统的稳定性.因此，为了精确标定系统特性，必须通过载荷识别的方式确定激励特性，而这部分工作尚未见成熟的体系.第四，系统辨识是一项面向工程应用的课题，在辨识方法推广之前，其收敛性、可靠性必须经过实验的验证.然而，目前时滞耦合系统的结构设计、参数规划及时滞调节等技术仍无成熟经验可循，而相应的成果也鲜见发表.因此，在系统辨识算法的实验验证工作上，我们将面临更多的技术尝试和探索.这4个方面的难题归纳成科学问题就是时滞耦合线性系统的可辨识性分析及算法构造、时滞耦合非线性系统的辨识理论及算法构造、时滞耦合系统的载荷识别理论及算法构造和时滞耦合系统辨识算法的实验验证.另外，是否可以将针对无时滞系统提出的新的辨识方法应用到耦合时滞系统的辨识中，也是一个值得研究的问题[110-111].

(2)中立型时滞系统的非线性动力学

振动控制中广泛采用加速度传感器，越来越多的研究表明，直接采用加速度反馈具有良好的控制性能，但加速度传感器测得的信号常常受到高频噪声的扰动，需要低通滤波器过滤掉高频噪声，而滤波器存在难以避免的时滞，从而加速度反馈具有时滞效应，这样就会得到中立型时滞系统[112116].在该类型的系统中时滞出现在最高阶导数上，不同于滞后型微分方程，采用中立型微分方程描述的系统的定性理论还有待进一步完善.例如，分析系统的非线性动力学时，适用于滞后性方程的理论方法是否可以全部移植到中立型方程是一个值得研究的问题，特别是对于那些在滞后性方程中已经得到较好解决的问题，如高余维分岔分析、动力学分类、吸引域估计等，是否还能使用相同的方法得到相似的结论目前尚未完全清楚.另外，将滞后型方程理论与控制理论结合起来研究具体的控制问题目前已相当成熟，但是中立型方程理论是否可以嵌入到控制理论框架中从而发展出针对采用加速度传感器进行信号采集的实际系统的一般性时滞控制理论，将是一个具有重要理论与应用价值、同时具有巨大挑战性的课题.

5.2 涉及具体对象的时滞系统动力学应用问题

(1)状态依赖时滞耦合Internet拥塞控制系统的振荡与同步

经过近 30年的研究，虽然对网络动力学的一些基本方面有了初步的了解，但是没有解决的问题依然有很多，而这些问题成为制约网络技术进一步发展的瓶颈.具体来说，第一，如果以发包速率作为状态变量，那么从实际数据来看，计算机网络的动力学行为可能会非常复杂，而这些动力学现象出现的机制仍然不甚清楚，更不要说针对这些动力学现象提出相应的控制策略.第二，计算机网络是一个异常复杂的巨系统，直接对高维计算机网络的非线性动力学问题进行研究无疑是困难重重的，一个可行的研究方案是转而研究网络系统的各种同步振荡.同步既是一种现象，也可以被看作一种有效的降维手段.当用户发包速率出现同步振荡时，在振荡同时达到峰值的时刻整个网络系统可能因不堪重负而崩溃.当今广泛应用于计算机网络中的传输控制协议/主动队列管理 (transmission control protocol/active queue management，TCP/AQM)协议的设计初衷就是为了消除这种同步振荡.毫无疑问，网络的同步性能与拓扑结构具有密切的联系，例如对于无标度网络，可以预计具有相同度的节点的振荡也具有某种同步性.如何定量刻画同步类型与拓扑结构的关系是一个尚未解决而又值得关注的问题.第三，拥塞是如何像波一样在网络上传播的？为何有时候拥塞只发生在局部，而有时一个局部的拥塞却会像病毒一样扩散到整个网络从而使得网络系统瘫痪？其完整的数学模型含有状态依赖时滞，而且这个时滞不可忽略,否则将产生奇异性.这给从理论上对该问题进行研究带来极大的挑战.第四，无线网络的应用正变得越来越普遍，即使是在工业和科学研究领域，无线网络的作用也变得越来越重要.例如，在机器人网络中，为了实现某种同步运动或相互协同完成任务，机器人个体之间需要通信并据此发出控制指令以调整自己的运动状态.无线网络信号的传输时滞也是依赖于状态的，那么如何设计网络拓扑结构以保证拥塞控制算法的有效性，是设计可靠的机器人网络的前提.以上几个方面的问题归纳成科学问题就是计算机网络中以状态依赖时滞为中心的复杂非线性动力学机制、状态依赖时滞耦合网络的同步与去同步、通过状态依赖时滞耦合的机械网络与计算机网络特别是无线网络的稳定性与同步优化.

(2)磨削的时滞动力学建模、颤振机理及其控制

从20世纪40年代以来，数控加工 (numerical control machining)技术的逐渐兴起，促使人们将注意力逐渐从人员素质转向了加工过程本身.数控机床在收到计算机的指令之后，会自动地按照要求进行加工生产，中间几乎不需要任何人工干预，因此，提前预测加工过程本身的行为，对于确保机械加工平稳进行、规避一些“加工雷区”，具有极其重要的指导意义.加工过程中的再生颤振是加工过程需要解决的最主要问题.经典的观点认为这种颤振是工件和砂轮之间的摩擦力引发的，近年来，研究发现再生颤振与磨削的厚度及其磨削的转速(可以对应到模型中的时滞)有关，因此，再生颤振的诱发是摩擦力和转速联合作用的结果，这个过程中的摩擦是时变的，而且磨削厚度在空间和时间尺度上都有不确定性.磨削动力学模型中的时滞、摩擦力、非线性、非光滑和变参数等因素，都给分析与抑制磨削颤振带来了巨大的挑战.和简单的线性系统相比，时滞将系统的维数扩展到无穷维；摩擦力给颤振引入黏滑机制；非线性导致张弛振荡和涡动等效应；磨削力中的非光滑接触带来多重时滞效应；变参数导致快慢变特性.要解决这一问题，面临的挑战在于：第一、如何建立能够准确描述磨削加工过程的动力学模型，从而揭示诱发磨削颤振的重要因素？第二、不同的颤振形式，特别是由再生效应和摩擦效应分别导致的磨削颤振，都是如何产生的，各自又有怎样的特征？第三，如何最有效地消除或者削弱磨削颤振?

(3)时滞非线性隔振器动力学特性及控制机理

经典的线性隔振器的优化方法有降低刚度和增大阻尼这两种方式，但是这样的优化方法在分析和应用过程中出现了矛盾，矛盾主要表现在：通过减小弹性元件的刚度来扩大有效隔振频带会降低系统的承载能力；而通过增大阻尼降低共振峰值会恶化高频范围的隔振效果.为了协调这样的矛盾，近年来开始出现利用非线性控制方法构造新型隔振器的趋势.一方面，充分利用结构本身的非线性特性实现提高静荷载承载能力和降低动态刚度，即所谓的“高静低动”，而非线性阻尼特性有助于隔振结构在高频范围内的振动隔离性能的提升.另一方面，时滞控制的引入不但充分利用了时滞对动力学特性的“开关”作用，还挖掘出时滞与非线性特性联合作用下对系统振动能量的转移、抑制的影响.因此，针对提升隔振器在不同频带内性能的要求，并且充分考虑和利用时滞非线性动力学的成果，可以考虑利用非线性和时滞控制构造新型智能隔振器，并对其进行动力学特性分析、结构参数优化、时滞控制机理和实验方法的研究.所要研究解决的问题主要来源于以下三个方面：第一，如何利用结构几何特性实现可调节非线性特性，能够使隔振器产生高静低动的特征，能否在理论层面给出有效判据使得非线性特性得到充分利用？第二，在对非线性隔振器进行参数设计和振动控制的过程中，如何通过理论分析方法建立控制参数和不同频带上隔振效果的关系，以确定最优的参数范围？第三，提出的非线性结构和时滞控制方法如何作动在系统上，控制参数与非线性特性联合作用的振动具有怎样的特征？上述三个方面的问题和需求归纳成科学问题就是：(1)基于高静低动特性的非线性隔振元件的结构参数优化判据；(2)时滞控制非线性隔振器不同频带内的控制机理；(3)时滞控制非线性隔振器的实验方法与实现.此外，是否可以更好地利用强非线性的特点进行有效隔振以及在实现时滞耦合时如何更加灵活地进行采样与作动也是具有重要科学与实际意义、同时具有一定挑战性的学术问题[117-118].

1 Xu J,Chung KW.Dynamics for a class of nonlinear systems with time delay.Chaos,Solitons and Fractals,2009,40(1)：28-49

2胡海岩，王在华.非线性时滞动力系统的研究进展.力学进展，1999,29：501-512(Hu Haiyan,Wang Zaihua.Review on nonlinear dynamic systems involving time delays.Advances in Mechanics,1999,29：501-512(in Chinese))

3徐鉴，裴利军.时滞系统动力学近期研究进展与展望.力学进展,2006,36：17-30(Xu Jian,Pei Lijun.Advances in dynamics for delayed systems.Advances in Mechanics,2006,36：17-30(inChinese))

4 Liu ZH,Payre G.Stability analysis of doubly regenerative cylindrical grinding process.Journal of Sound and Vibration,2007,301(3-5)：950-962

5 Sipahi R,Atay FM,Niculescu SI.Stability of traffic fl w behavior with distributed delays modeling the memory e ff ects of the drivers.SIAM Journal of Applied Mathematics,2007,68(3-5)：738-759

6王在华，胡海岩.时滞动力系统的稳定性与分岔：从理论走向应用.力学进展,2013,43(1)：3-19(Wang Zaihua,Hu Haiyan.Stability and bifurcation of delayed dynamic systems：from theory to application.Advances in Mechanics,2013,43(1)：3-19(in Chinese))

7徐鉴.振动控制研究进展综述.力学季刊,2015,36(4)：547-565(Xu Jian.Advances of research on vibration control.Chinese Quarterly of Mechanics,2015,36(4)：547-565(in Chinese))

8 ErzgraberE,KrauskopfB,LenstraD.Bifurcationanalysisofasemiconductor laser with filtere optical feedback.SIAM Journal of Applied systems,2007,6(1)：1-28

9 Green K.Stability near threshold in a semiconductor laser subject to optical feedback：a bifurcation analysis of the Lang-Kobayashi equations.Physical Review E,2009,79(3)：036210

10 Campbell SA,Yuan Y.Zero singularities of codimension two and three in delay di ff erential equations.Nonlinearity,2008,21(11)：2671-2691

11 Xu J,Chung KW.A perturbation-incremental scheme for studying Hopf bifurcation in delayed di ff erential systems.Science in China Series E,2009,52(3)：698-708

12 Xu J,Chung KW.An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks.SIAM Journal on Applied Systems,2007,6(1)：29-60

13 Xu J,Chung KW.Double Hopf bifurcation with strong resonances in delayed systems with nonlinearities.Mathematical Problems in Engineering,2009,2009(4)：266-287

14 Liu ZH,Zhu WQ.Compensation for time-delayed feedback bangbang control of quasi-integrable Hamiltonian systems.Science in China Series E,2009,52(3)：688-697

15 Zhen B,Xu J.Fold-Hopf bifurcation analysis for a coupled FitzHugh-Nagumo neural system with time delay.International Journal of Bifurcation and Chaos,2010,20(12)：3919-3914

16 Wang WY,Xu J.Multiple scales analysis for double Hopf Bifurcation with 1：3 resonance.Nonlinear Dynamics,2011,66(1-2)：39-51

17 Wang WY,Xu J.Strong and weak resonances in delayed di ff erential systems.International Journal of Bifurcation and Chaos,2013,23(7)：1350119

18 Song ZG,Xu J.Stability switches and double Hopf bifurcation in a two-neural network system with multiple delays.Cognitive Neurodynamics,2013,7(6)：505-521

19 Song YL,Han Y,Peng Y.Stability and Hopf bifurcation in an unidirectional ring of n neurons with distributed delays.Neurocomputing,2013,121(2)：442-452

20 Chen YL,Xu J.Applications of the integral equation method to delay di ff erential equations.Nonlinear Dynamics,2013,73(4)：2241-2260

21 Li JY,Zhang L,Wang ZH.A simple algorithm for the stability testing of periodic solutions of some nonlinear oscillators with large time-delay.Science in China Series E:Technological Sciences,2011,54(8)：2033-2043

22 Wang ZH.A very simple criterion for characterizing the crossing direction of time-delay systems with delay-dependent parameters.International Journal of Bifurcation and Chaos,2012,22(3)：1250048

23 Zhang L,Wang HL,Hu HY.Symbolic computation of normal form for Hopf bifurcation in a retarded functional di ff erential equation with unknown parameters.Communications in Nonlinear Science and Numerical Simulation，2012,17(8)：3328-3344

24 Zhang L,Wang HL,Wang ZH.Symbolic computation of normal form for Hopf bifurcationin a neutral delay di ff erential equation and an applicationto a controlled crane.Nonlinear Dynamics,2012,70(1)：463-473

25 Yan Y,Xu J,Wang WY.Nonlinear chatter with large amplitude in a cylindrical plunge grinding process.Nonlinear Dynamics,2012,69(4)：1781-1793

26 Yan Y,Xu J,Wiercigroch M.Chatter in a transverse grinding process.Journal of Sound and Vibration,2014,333(3)：937-953

27 Ge JH,Xu J.Hopf bifurcation and chaos in an inertial neuron system with coupled delay.Science China:Technological Sciences,2013,56(9)：2299-2309

28 Ge JH,Xu J.Weak resonant double Hopf bifurcations in an inertial four-neuron model with time delay.International Journal of Neural Systems,2012,22(1)：63-75

29 Ge JH,Xu J.Stability switches and fold-Hopf bifurcations in an inertial four-neuron network model with coupling delay.Neurocomputing,2013,110(8)：70-79

30 Jiang J,Song YL.Bogdanov-Takens bifurcation in an oscillator with negative damping and delayed position feedback.Applied Mathematical Modelling,2013,37(16-17)：8091-8105

31 Song ZG,Xu J.Stability switches and Bogdanov-Takens bifurcation in an inertial two-neurons coupling system with multiple delays.Science China:Technological Sciences,2014,57(5)：893-904

32 Song ZG,Xu J.Codimension-two bursting analysis in the delayed neural system with external stimulations.Nonlinear Dynamics,2012,67(1)：309-328

33 Song ZG,Xu J.Stability switches and multistability coexistence in a delay-coupled neural oscillators system.Journal of Theoretical Biology,2012,313(21)：98-114

34徐鉴，陈振.时滞对轴流压气机喘振的影响.中国科学：物理学力学天文学，2013，43(4)：380-389(Xu Jian，Chen Zhen.E ff ects of delay on surge in axial compressors.Science in China(Series G),2013,43(4)：380-389(in Chinese))

35 Zhen B,Xie WP,Xu J.A nonlinear analysis for the lateral vibration of footbridges induced by pedestrians.ASCE:Journal of Bridge Engineering,2013,18(2)：122-130

36 Zhen B,Wong WK,Xu J,et al.Application of Nakamura’s model to describe the delayed increase in lateral vibration of footbridges.ASCE:Journal of Engineering Mechanics,2012,139(12)：1708-1713

37 Zhen B,Luo W,Xu J.Analysis of critical velocities for an infinit timoshenko beam resting on an elastic foundation subjected to a harmonic moving load.Shock and Vibration,2014,2014(2)：848536

38 Hu HY.Using delayed state feedback to stabilize periodic motions of an oscillator.Journal of Sound and Vibration,2004,275(s3-5)：1009-1025

39 Xu J,Chung KW.E ff ects of time delayed position feedback on a van der Pol-Duffing oscillator.Physica D,2003,180(1-2)：17-39

40 Liu B,Hu HY.Group delay induced instabilities and Hopf bifurcations of a controlled double pendulum.International Journal of Non-Linear Mechanics,2010,45(4)：442-452

41 Ohta T,Murakami T.A Stabilization control of bilateral system with time delay by vibration index-application to inverted pendulum Control.IEEE Transactions on Industrial Electronics,2009,56(5)：1595-1603

42 Landry M,Campbell SA,Morris K,et al.Dynamics of an inverted pendulum with delayed feedback control.SIAM Journal on Applied Dynamical Systems,2005,4(2)：333-351

43 Campbell SA,Crawford S,Morris K.Friction and the inverted pendulum stabilization problem.Journal of Dynamic Systems Measurement and Control,2008,130(5)：054502

44 Olgac N,Holm-Hansen BT.A novel active vibration absorption technique：delayed resonator.Journal of Sound and Vibration,1994,176(1)：93-104

45 Filipovi´c D,Olgac N.Delayed resonator with speed feedback including dual frequency-theory and experiments//Proceedings of the 36th Conference on Decision&Control,1997：2535-2540

46赵艳影，徐鉴.时滞动力吸振器及其对主系统振动的影响.振动工程学报，2006,19(4)：548-552(Zhao Yanying,Xu Jian.Delayed resonator and its e ff ects on vibrations in primary system.Journal of Vibration Engineering,2006,19(4)：548-552(in Chinese))

47 Zhao YY,Xu J.E ff ects of delayed feedback control on nonlinear vibration absorber system.Journal of Sound and Vibration,2007,308：212-230

48赵艳影,徐鉴.时滞非线性动力吸振器的减振机理.力学学报,2008,40(1)：98-106(Zhao Yanying,Xu Jian.Mechanism analysis of delayed nonlinear vibration absorber.Chinese Journal of Theoretical and Applied Mechanics,2008,40(1)：98-106(in Chinese))

49 Zhang XX,Xu J.Identificatio of time delay in nonlinear systems with delayed feedback control.Journal of the Franklin Institute,2015,352(8)：2987-2998

50 Zhang XX,Xu J,Huang Y.Experiment on parameter identifica tion of a time delayed vibration absorber.IFAC Papersonline,2015,48(12)：57-62

51 Zhang X,Xu J,Feng Z.Nonlinear equivalent model and its identificatio for a delayed absorber with magnetic action using distorted measurement.Nonlinear Dynamics,2017,88(2)：937-954

52 Sun YX,Xu J.Experiments and analysis for a controlled mechanical absorber considering delay e ff ect.Journal of Sound and Vibration,2015,339：25-37

53 Xu J,Sun YX.Experimental studies on active control of a dynamic system via a time-delayed absorber.Acta Mechanica Sinica,2015,31(2)：229-247

54 Sun XT,Xu J,Jing XJ,et al.Beneficia performance of a quasi-zerosti ff ness vibration isolator with time-delayed active control.International Journal of Mechanical Science,2014,82(1)：32-40

55 Sun XT,Jing XJ,Xu J,et al.Vibration isolation via a scissor-like structured platform.Journal of Sound and Vibration,2014,333(9)：2404-2420

56 Sun XT,Jing XJ,Xu J,et al.A quasi-zero-sti ff ness-based sensor system in vibration measurement.IEEE Transactions on Industrial Electronics,2014,61(10)：5606-5614

57 Sun XT,Jing XJ,Xu J,et al.A 3D quasi-zero-sti ff ness based sensor system for absolute motion measurement and application in active vibration control.IEEE/ASME Transactions on Mechatronics,2015,20(1)：254-262

58 Song ZG,Xu J.Bifurcation and chaos analysis on a delayed twoneural network with the variation slope ratio in activation function.International Journal of Bifurcation and Chaos,2012,22(5)：1250105

59 Zhao YY,Xu J.Using the delayed feedback control and saturation control to suppress the vibration of the dynamical system.Nonlinear Dynamics,2012,67：735-753

60赵艳影，徐鉴.利用时滞反馈控制自参数振动系统的振动.力学学报，2011，43(5)：894-904(Zhao Yanying，Xu Jian.Using the delayed feedback to control the vibration of the auto-parametric dynamical system.Chinese Journal of Theoretical and Applied Mechanics,2011,43(5)：894-904(in Chinese))

61 Yan Y,Xu J.Suppression of regenerative chatter in a plungegrinding process by spindle speed.Journal of Manufacturing Science&Engineering,2013,135(4)：041019

62 Zhang S,Xu J.Time-vary delayed feedback control for an Internet congestion control model.Discrete and Continuous Dynamical Systems-Series B,2011,2(2)：653-668

63 Zhang S,Xu J.Oscillation control for n-dimensional congestion control model via time-varying delay.Science in China Series E：Technological Sciences,2011,54(8)：2044-2053

64 Zhang S,Xu J.Bursting-like motion induced by time-varying delay in an internet congestion control model.Acta Mechanica Sinica,2012,28(4)：1169-1179

65 Zhang S,Xu J.Oscillatory dynamics induced by time delay in an internet congestion control model with ring topology.Applied Mathematics and Computation,2012,281(22)：11033-11041

66 Zhang S,Xu J.Quasiperiodic motion induced by heterogeneous delays in a simplifieinternet congestion control model.Nonlinear Analysis:Real World Applications,2013,14(1)：661-670

67 Zhang S,Chung KW,Xu J.Stability switch boundaries in an internet congestion control model with diverse time delays.International Journal of Bifurcation and Chaos,2013,23(5)：1330016

68 Zhang S,Xu J.On the stability and multi-stability of a TCP/RED congestion control model with state-dependent delay and discontinuous marking function.Communications in Nonlinear Science and Numerical Simulation,2015,22(1-3)：269-284

69 Zhou YS,Wang ZH.Optimal feedback control for linear systems with input delays revisited.Journal of Optimization Theory and Applications,2014,163(3)：989-1017

70朱霖河，赵洪涌.时滞惯性神经网络的稳定性和分岔控制.物理学报，2014，63(9)：090203(Zhu Linhe，Zhao Hongyong.Stability and bifurcation control in inertial neuron networks with delays.Acta Physica Sinica,2014,63(9)：090203(in Chinese))

71郑远广，王在华.含时滞的快--慢耦合系统的动力学研究进展.力学进展，2011，41：400-410(Zheng Yuanguang，Wang Zaihua.Advances in dynamics of slow-fast systems with time delay.Advances in Mechanics,2011，41：400-410(in Chinese))

72 England JP,Krauskopf B,Osinga HM.Computing two-dimensional global invariant manifolds in slow-fast systems.International Journal of Bifurcation and Chaos,2007,17(3)：805-822

73 Branicki M,Wiggins S.An adaptive method for computing invariant manifolds in non-autonomous,three-dimensional dynamical systems.Physica D,2009,238(16)：1625-1657

74 Vakakis AF,Rand RH.Nonlinear dynamics of a system of coupled oscillators with essential sti ff ness nonlinearities.International Journal of Non-Linear Mechanics,2004,39(7)：1079-1091

75 Pirbodaghi T,Hoseini S.Nonlinear free vibration of a symmetrically conservative two-mass system with cubic nonlinearity.Journal of Computation and Nonlinear Dynamics,2009,5(1)：011006

76 Lee YS,Vakakis AF,Bergman LA,et al.Passive non-linear targeted energy transfer and its applications to vibration absorption：A review.Journal of Multi-body Dynamics,2008,222(2)：77-134

77 Laxalde D,Thouverez F,Sinou JJ.Dynamics of a linear oscillator connected to a small strongly non-linear hysteretic absorber.International Journal of Nonlinear Mechanics,2006,41(8)：969-978

78 Zheng YG,Wang ZH.Stability and Hopf-bifurcation of a class of TCP/AQM networks.Nonlinear Analysis:Real World Applications,2010,11(11)：1552-1559

79 Zheng YG,Wang ZH.Delayed Hopf-bifurcation in time-delayed slow-fast systems.Science China Technological Sciences,2010,53(2)：656-663

80 Jiang SY,Xu J,Yan Y.Stability and oscillations in a fast-slow fl xible joint system with transformation delay.Acta Mechanica Sinica,2014,30(5)：727-738

81 Xu J,Jiang SY.Delay-induced Bogdanov-Takens bifurcation and dynamical classification in a slow-fast fl xible joint system.International Journal of Bifurcation and Chaos,2015,25(9)：1550121

82郑远广，黄承代，王在华.反馈时滞对van der Pol振子张弛振荡的影响.力学学报，2012，44(1)：148-157(Zheng Yuanguang，Huang Chengdai，Wang Zaihua.Delay e ff ect on the relaxasion oscillations of a van der pol oscillator with delayed feedback.Chinese Journal of Theoretical and Applied Mechanics,2012,44(1)：148-157(in Chinese))

83 Zheng YG,Wang ZH.Stability analysis of nonlinear dynamic systemswithslowlyandperiodicallyvaryingdelay.Communicationsin Nonlinear Science and Numerical Simulation,2012,17(10)：3999-4009

84 Zheng YG,Wang ZH.Relaxation oscillation and attractive basins of a two-neuron Hopfiel network with slow and fast variables.Nonlinear Dynamics,2012,70(2)：1231-1240

85 Zheng YG,Wang ZH.Time-delay e ff ect on the bursting of the synchronized state of coupled Hindmarsh-Rose neurons.Chaos,2012,22：043127

86 Pare D,Curro’Dossi R,Steriade M.Neuronal basis of the Parkinsonian resting tremor：A hypothesis and its implications for treatment.Neuroscience,1990,35(2)：217-226

87 Feng CF,Zhang Y,Sun JT,et al.Generalized projective synchronization in time-delayed chaotic systems.Chaos,Solitons and Fractal,2008,38(3)：743-747

88 Ghosh D.Generalized projective synchronization in time-delayed systems：Nonlinear observer approach.Chaos,2009,19：013102

89 Fridman E,Shaked U.H-infinitcontrol of linear state-delay descriptor systems：An LMI approach.Linear Algebra Application，2002,351-352：271-302

90 WangQY,LuQS.Phasesynchronizationinsmallworldchaoticneural networks.Chinese Physical Letter,2005,22(6)：1329-1332

91 Li CG,Chen LN,Aihara K.Synchronization of coupled nonidentical genetic oscillators.Physical Biology,2006,3(1)：33-37

92 Huang H,Feng G.Synchronization of nonidentical chaotic neural networks with time delays.Neural Networks,2009,22(7)：869-874

93 Song YL,Tad´e MO.Bifurcation analysis and spatio-temporal patterns of nonlinear oscillations in a delayed neural network with unidirectional coupling.Nonlinearity,2009,22(5)：975-1001

94 Song YL,Makarov VA,Velarde MG.Stability switches,oscillatory multistability,and spatio-temporal patterns of nonlinear oscillations in recurrently delay coupled neural networks.Biological Cybernatics,2009,101(2)：147-167

95 Tass PA.Phase Resetting in Medicine and Biology：Stochastic Modeling and Data Analysis.Berlin：Springer,1999

96 Tass PA.A model of desynchronizing deep brain stimulation with a demand-controlled coordinated reset of neural subpopulations.Biological Cybernetics,2003,89(2)：81-88

97 Tukhlina N,Rosenblum M.Feedback suppression of neural synchrony in two interacting populations by vanishing stimulation.Journal of Biological Physics,2008,34(3)：301-314

98 Luo M,Xu J.Washout filte aided mean fiel feedback desynchronization in an ensemble of globally coupled neural oscillators.Biological Cybernetics,2009,101(3)：241-246

99 Strogatz SH,Abrams DM,Mcrobie A,et al.Crowd synchrony on the Millennium Bridge.Nature,2005,438(7064)：43-44

100 Eckhardt B,Ott E,Strogatz SH,et al.Modeling walker synchronization on the Millennium Bridge.Physical Review E,2007,75：021110

101 Wong KW,Zhen B,Xu J et al.An analytic criterion for generalized synchronization in unidirectionally coupled systems based on the auxiliary system approach.Chaos,2012,22：033146

102 Wang L,Zhen B,Xu J.A simple approach to achieve modifie projective synchronization between two di ff erent chaotic systems.The Scientifi World Journal,2013,2013：568194

103 Song YL,Xu J.Inphase and antiphase synchronization in a delaycoupled system with applications to a delay-coipled FitzHugh-Nagumo system. IEEE Transactions on Neural Networks and Learning Systems,2012,23(10)：1659-1670

104 Song YL.Hopf bifurcation and spatio-temporal patterns in delaycoupled van der Pol oscillators.Nonlinear dynamics,2011,63(1-2)：223-237

105 Song YL,Xu J,Zhang TH.Bifurcation,amplitude death and oscillation patterns in a system of three coupled van der Pol oscillators with di ff usively delayed velocity coupling.Chaos,2011,21：023111

106 Ge JH,Xu J.Synchronization and synchronized periodic solution in a simplifie fve-neuron BAM neural network with delays.Neuro-computing,2011,74(6)：993-999

107 Sun XT,Xu J.Delay induced resonances in a system of coherent interaction of lasers.Journal of Vibration Engineering and Technology,2014,2(2)：141-156

108 Wang L,Zhao HY.Synchronized stability in a reaction–di ff usion neural network model.Physics Letters A,2014,378(48)：3586-3599

109 Luo M,Xu J.Suppression of collective synchronization in system of neural groups with washout-filte aided feedback.Neural Networks,2011,24(6)：538-543

110邓杨,彭志科,杨扬等.基于参数化时频分析的非线性振动系统参数辨识.力学学报,2013，45(6)：992-996(De Yang,Peng Zhike,Yang Yang,et al.Identificatio of nonlinear vibration systems based on parametric TFA.Chinese Journal of Theoretical and Applied Mechanics,2013,45(6)：992-996(in Chinese))

111谢永,刘盼,蔡国平.基于加速度信号的柔性板的挠性参数辨识.力学学报,2014，46(1)：128-135(Xie Yong,Liu Pan,Cai Guoping.Parameter identificatio of fl xible plate based on the acceleration output.Chinese Journal of Theoretical and Applied Mechanics,2014,46(1)：128-135(in Chinese))

112 Xu Q,Wang ZH.Exact stability test of neural delay di ff erential equations via a rough estimation of the testing integral.International Journal of Dynamics and Control,2014,2(2)：154-163

113 Xu Q,Stepan G,Wang ZH.Delay-dependent stability analysis by using delay-independent integral evaluation.Automatica,2016,70：153-157

114 Xu Q,Stepan Gabor,Wang ZH.Balancing a wheeled inverted pendulum with a single accelerometer in the presence of time delay.Journal of Vibration and Control,2017,23(4)：604-614

115 He YQ,Han JD.Acceleration-feedback-enhanced robust control of an unmanned helicopter.Journal of Guidance,Control and Dynamics,2010,33(4)：1236-1250

116 Wang ZH,Hu HY,Xu Q,et al.E ff ect of delay combinations on stability and Hopf bifurcation of an oscillator with accelerationderivative feedback.International Journal of Nonlinear Mechanics,doi：10.1016/j.ijnonlinmec.2016.10.008

117高雪,陈前,刘先斌.一类分段光滑隔振系统的非线性动力学设计方法.力学学报,2016，48(1)：192-200(Gao Xue,Chen Qian,Liu Xianbin.Nonlinear dynamics design for piecewise smooth vibration isolation system.Chinese Journal of Theoretical and Applied Mechanics,2016,48(1)：192-200(in Chinese))

118王在华,胡海岩.具有采样反馈的力控制系统稳定性.力学学报,2016，48(6)：1372-1381(Wang Zaihua,Hu Haiyan.Stability of a force control system with sampled-data feedback.Chinese Journal of Theoretical and Applied Mechanics,2016,48(6)：1372-1381(in Chinese))

REVIEW ON NONLINEAR DYNAMICS IN SYSTEMS WITH COULPLING DELAYS1)

Zhang Shu Xu Jian2)
(School of Aerospace Engineering and Applied Mechanics，Tongji University，Shanghai 200092，China)

With the deep understanding towards the objective laws of nature,requirements on refinemen and complexity in engineering system design are increasing.Many coupled dynamic system designs need to take into account the dynamics induced by the time delay existing in the coupling process.Such coupling time delay may come from the process of coupling with the sensing system,the actuation system and the control system.Coupling delays also extensively exist in the field such as transportation system,system biology,electronic communication,neural and information networks and etc.Firstly,based on the concept of coupling delay,this paper reviews the recent research progresses on dynamics induced by such delay from the following four aspects：(1)the delay-centered mechanism of complex dynamics in coupled systems;(2)experimental foundation and realization of stabilizing coupled systems by utilizing time delay;(3)dynamics of fast-slow coupled system with time delay;and(4)synchronization and desynchronization of delayed neural networks.Some advances in the general theory of systems with coupling delay are highlighted including the coupling-delay-induced bifurcation and singularity with high codimention and the novel quantitative method of analysis,normal form computation for neutral delay di ff erential equations,identificatio of time delay and nonlinear parameters in nonlinear systems with coupling delay and the relevant experiment,relaxation oscillation in the fast-slow system with coupling delay,and transition of modes of synchronization induced by coupling delay in network systems.Secondly,as for the application,some new results are presented in details such as the coupling-delay-induced chatter in grinding process and its mechanism,bifurcation with high codimension and complex dynamics induced by coupling delay in neural networks with inertial terms,and design and experiments of vibration absorber and isolator using coupling delay.Finally,some problems which are worthy of attention in near future are highlighted from perspectives of the general theory of systems with coupling delay and the potential applications.

system with coupling delays,nonlinear dynamics,delayed di ff erential equation,fast-slow system,neural network

O313，TP183

：A

10.6052/0459-1879-17-123

2017–04–13 收稿，2017–04–20 录用,2017–04–21 网络版发表.

1)国家自然科学基金资助项目(11572224,11502168,11032009).

2)徐鉴，教授，主要研究方向：非线性动力学.E-mail：xujian@tongji.edu.cn

张舒,徐鉴.时滞耦合系统非线性动力学的研究进展.力学学报,2017,49(3)：565-587

Zhang Shu,Xu Jian.Review on nonlinear dynamics in systems with coulpling delays.Chinese Journal of Theoretical and Applied Mechanics,2017,49(3)：565-587