振动激发对高超声速气动力/热影响1)

张子健刘云峰 姜宗林

(中国科学院力学研究所高温气体动力学国家重点实验室，北京100190)(中国科学院大学，北京100049)

-流体力学

振动激发对高超声速气动力/热影响1)

张子健2)刘云峰 姜宗林

(中国科学院力学研究所高温气体动力学国家重点实验室，北京100190)(中国科学院大学，北京100049)

随着飞行马赫数的不断提高，空气的高温气体效应越来越明显，对高超声速飞行器的气动力/热特性产生重要影响.高温气体效应对气动力/热的影响机理复杂，影响参数众多，迄今为止国内外尚未完全研究清楚.发生高温气体效应时，多个非线性物理过程耦合在一起，地面试验和数值模拟无法将这些过程解耦，无法给出关键物理机理.为了解决这一问题，文章提出一种理论分析与数值模拟相结合的两步渐进新方法：先通过牛顿迭代法得到发生振动激发过程的斜激波无黏解；再将该无黏解的结果作为边界条件，求解边界层的黏性解.利用该方法研究了振动激发过程对二维斜劈的气动力/热特性的影响规律.研究结果表明，振动激发过程对斜激波后的温度、密度、马赫数、雷诺数和斜激波角影响较大，而对压力和速度影响较小.斜激波波后的无黏流动与边界层流动是耦合在一起的.发生振动激发后，斜激波波后雷诺数的增大会导致边界层厚度减小，结合多个物理量的变化，如速度增大和温度减小，共同对边界层内的摩擦阻力和气动热产生影响.对比完全气体的结果发现，振动激发使壁面摩阻升高，而使壁面热流降低.分别通过影响激波层和边界层，振动激发对摩阻的影响是弱耦合的，而对热流的影响则是强耦合的.

振动激发，气动力/热，边界层，高温气体效应

引言

近十几年来，高超声速飞行器由于具有巨大的战略价值，受到了许多国家的高度重视，成为世界航空航天领域的重要发展方向和研究热点.高超声速飞行器是指在大气层内实现高超声速机动飞行的飞行器，其飞行速度一般超过5倍声速，主要包括航天运载器、太空作战飞行器、高超声速巡航导弹、高超声速飞机等.

在高超声速飞行器的飞行过程中，高速空气经过激波压缩和黏性阻滞后减速，空气巨大的动能转变为热能，导致飞行器表面激波层和边界层内空气的温度急剧升高.空气分子在如此高的温度下将发生振动激发、解离和电离等热化学反应，这就是高温气体效应[14].在高温气体效应的影响下，空气介质性质发生变化，进而影响飞行器的外部流动，最终导致高超声速飞行器的气动力/热特性偏离完全气体理论的预测结果.

高温气体效应对高超声速飞行器气动力特性的影响最早是在航天飞机再入时所发生的“上仰异常”现象中发现的[511].与航天飞机大钝头体、大攻角再入不同的是，新一代高超声速飞行器的飞行空域为20～100km高度的临近空间，多采用乘波体或升力体构型，飞行器头部不会形成很强的弓形激波，而主要是斜激波.飞行马赫数为6～15时，斜激波后空气温度为600～2500K，发生的热化学反应主要是空气分子振动激发[34].另一方面，与航天飞机相比，新一代高超声速飞行器飞行时间长、飞行距离远，对其所受的气动力/热的预测精度要求非常高，希望实现精细控制.因此，非常有必要深入细致地研究空气分子振动激发对高超声速飞行器气动力/热特性的影响.

中国科学院力学研究所的JF12激波风洞[1213],是国际上首座可复现25～40km高空、马赫数5～9飞行条件、喷管出口直径Φ2.5/Φ1.5m、试验气体为洁净空气、试验时间超过100ms的超大型高超声速风洞.目前，在JF12复现激波风洞上正大量开展高温气体效应对气动力/热特性影响的研究，并取得了一些成果[14-15].

高温气体效应对高超声速飞行器气动力/热特性的影响主要体现在以下两个方面[34]：一是对激波形状和激波层内压力、温度等的影响，这将会影响飞行器表面的压力分布以及激波与激波相互作用、激波与边界层相互作用的位置和强度；二是对边界层内流动的影响，这将会直接影响飞行器的摩阻和热流.更重要的是，高温气体效应对激波和边界层的影响会相互耦合叠加，使其对气动力/热的影响机理变得极其复杂.

本文主要研究高温下空气分子振动激发对高超声速气动力/热的影响，暂时不考虑解离和电离等过程.先给出考虑振动激发的空气热力学模型，以及斜激波与边界层的求解方法；然后分别单独讨论振动激发对斜激波波后流场和边界层内壁面摩阻、热流的影响；最后采用两种方法分析斜激波和边界层共同考虑振动激发时，对气动力/热特性的影响，并讨论其影响机制.

1 热力学模型与研究方法

1.1 高温空气的热力学模型

常温下，空气一般不考虑热化学反应，按完全气体来处理，其比内能、比焓、比定压热容和比热比等满足以下热力学关系

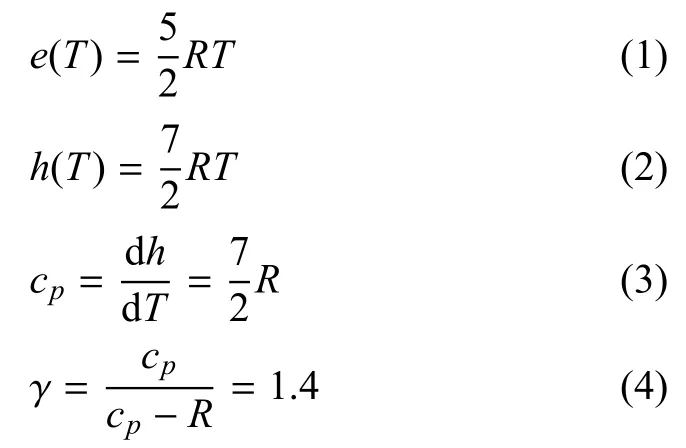
式中，R是空气的气体常数，取值288.28J/(kg·K).但考虑振动激发后，空气的比定压热容和比热比不再是常数，而是温度的非线性函数.为了简化分析，假设空气是由79%的N2和21%的O2组成的，则考虑振动激发后，比内能和比焓中将多出振动能项ev.

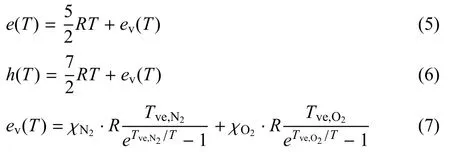
式中，χN2和χO2分别是N2和 O2的摩尔分数，而Tve,N2和Tve,O2是振动特征温度，取值为[16]

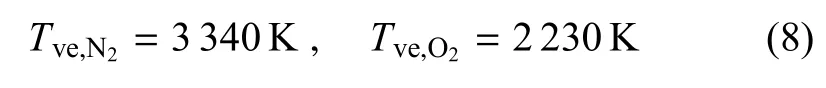
则比定压热容和比热比分别为

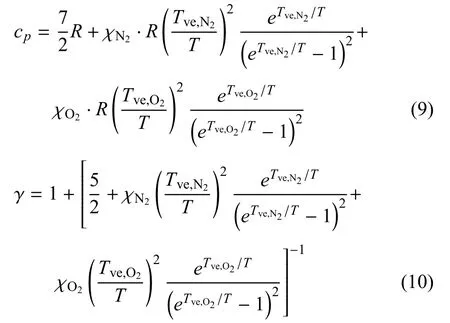
根据以上热力学关系，静止空气比振动能占比焓的比例以及空气比热比随温度的变化关系分别如图1所示.可见，当温度上升到800K时，空气振动能所占比例已达2.5%，比热比从1.4降低到1.353，此时振动激发对空气热力学性质的影响已不可忽略[2].当温度达到2500K时，空气振动能所占比例达12.6%，比热比降低到1.296，此时振动激发是相当可观的，空气的热力学性质将会发生较大变化，进而影响飞行器的外部流动，最终影响高超声速飞行器的气动力/热特性.

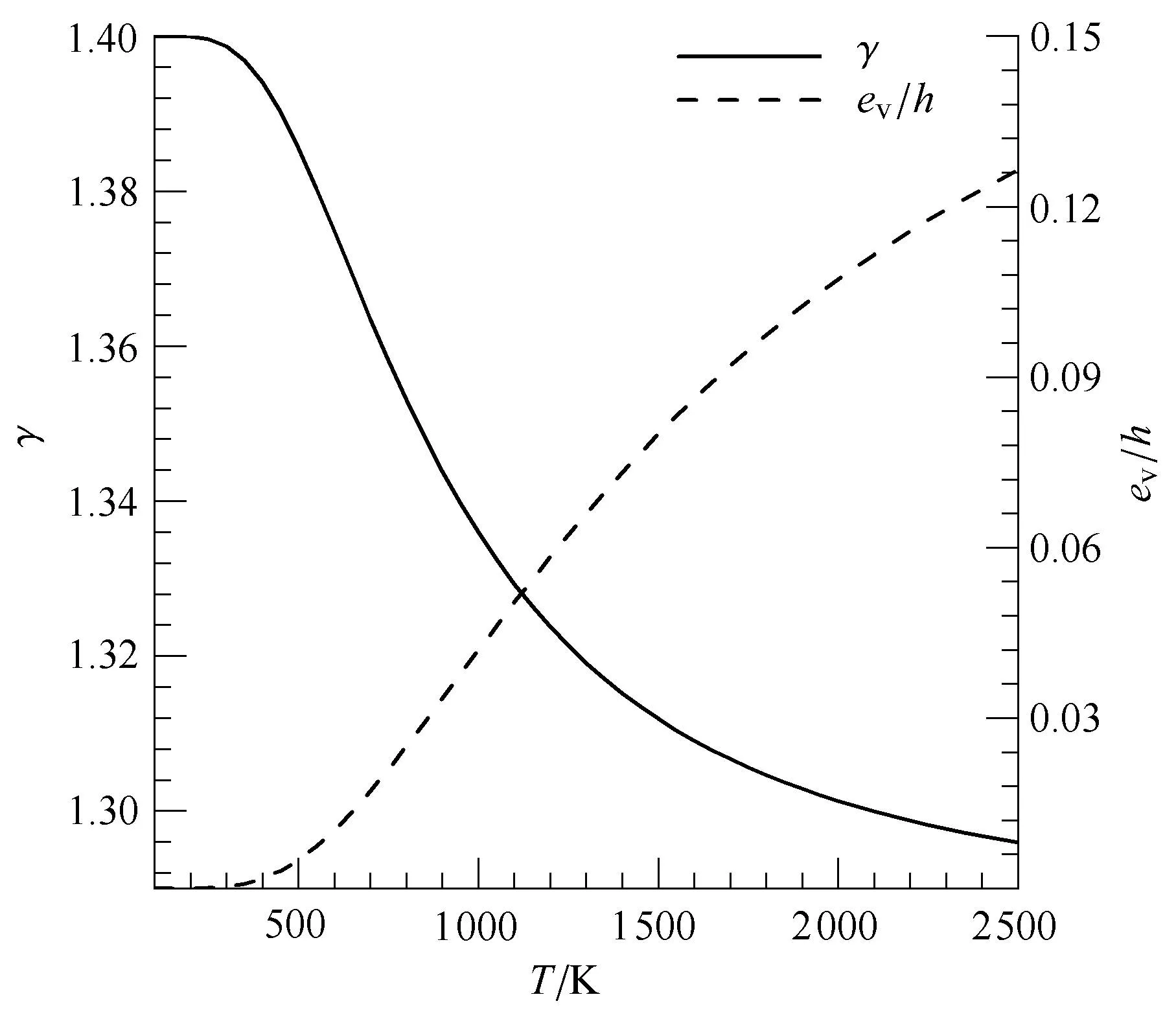
图1 静止空气比振动能占比焓的比例和空气比热比随温度的变化Fig.1 Variation of proportion of specifi vibration energy in specifi enthapy of stationary air and the specifi heat ratio with temperature

1.2 激波---边界层组合结构的两步渐进方法

本文提出一种理论求解斜激波与数值求解边界层相结合的两步渐进方法，将振动激发对激波和边界层的影响分开，来分析振动激发效应在激波层与边界层内的传递和干扰机理.高超声速飞行器的气动力/热特性是由其周围流场决定的，基本的流场结构是来流先经过一道激波压缩，然后通过边界层作用在飞行器壁面上.本文采用斜劈作为基本几何构型进行分析，将振动激发当成是一种扰动施加在流场上，如图2.

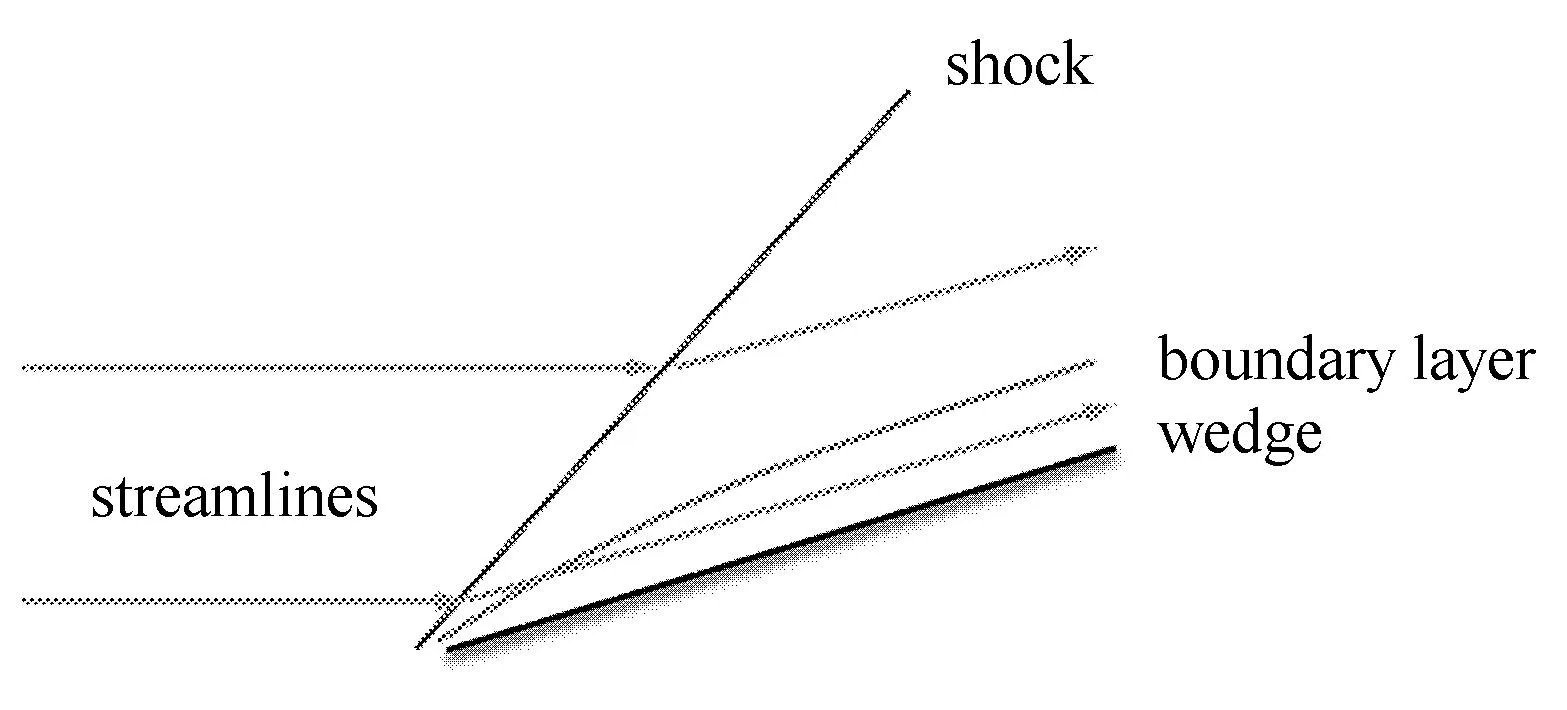
图2 流场示意图Fig.2 Schematic of the fl w fiel

根据边界层理论，壁面压力主要由斜激波波后压力决定，而摩阻和热流则主要由斜激波波后流动和边界层共同决定.于是，振动激发先对斜激波波后流场产生影响，使其压力、温度、速度等发生变化，从而对壁面压力产生影响；接着斜激波波后流动作为边界层的外流，其速度、温度的变化结合振动激发共同影响边界层内流动，最终影响壁面摩阻、热流.作为近似，忽略边界层对斜激波的反馈作用.这种近似方法在振动激发效应分析中的误差将在后续2.3.2节中进行简要说明.

因此，在渐进求解时，先求解斜激波关系，然后将斜激波波后流场参数作为平板边界层问题的来流参数进一步求解，最后根据边界层内流场得到壁面摩阻和热流.由于边界层内压力与外流压力非常接近，因此壁面压力可以直接取为斜激波后压力.另外，本文还直接求解黏性斜劈问题来验证以上两步渐进分析方法的准确性.

1.3 精确求解斜激波关系

考虑振动激发后，空气的焓是温度的非线性函数，难以得到解析的斜激波关系.本文从基本方程出发，推导出精确求解斜激波关系的牛顿迭代公式

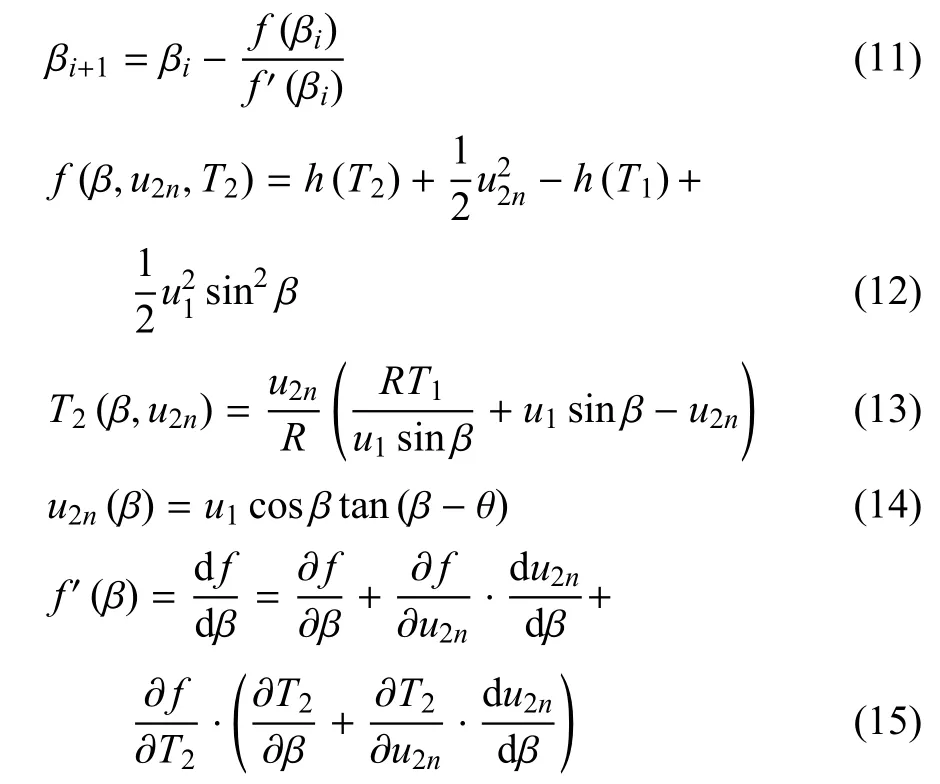
其中，β是斜激波角，θ是楔面角，其余流场参数的下标1表示激波前，下标2表示激波后，下标n表示垂直于激波的分量.对于完全气体，h(T)采用式(2)进行计算，而对于振动激发，h(T)则采用式(6)进行计算.根据以上牛顿迭代公式可以求出斜激波角β，进而求出所有斜激波波后流场参数.

1.4 数值求解边界层问题

控制方程采用二维Navier-Stokes方程[17-18]

其中，U为守恒变量，F,G分别为x,y方向的无黏守恒通量，Fv,Gv分别为x,y方向的黏性守恒通量，具体形式为

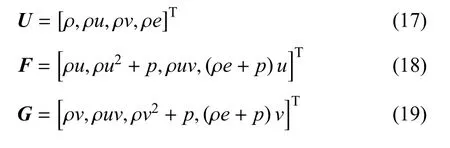
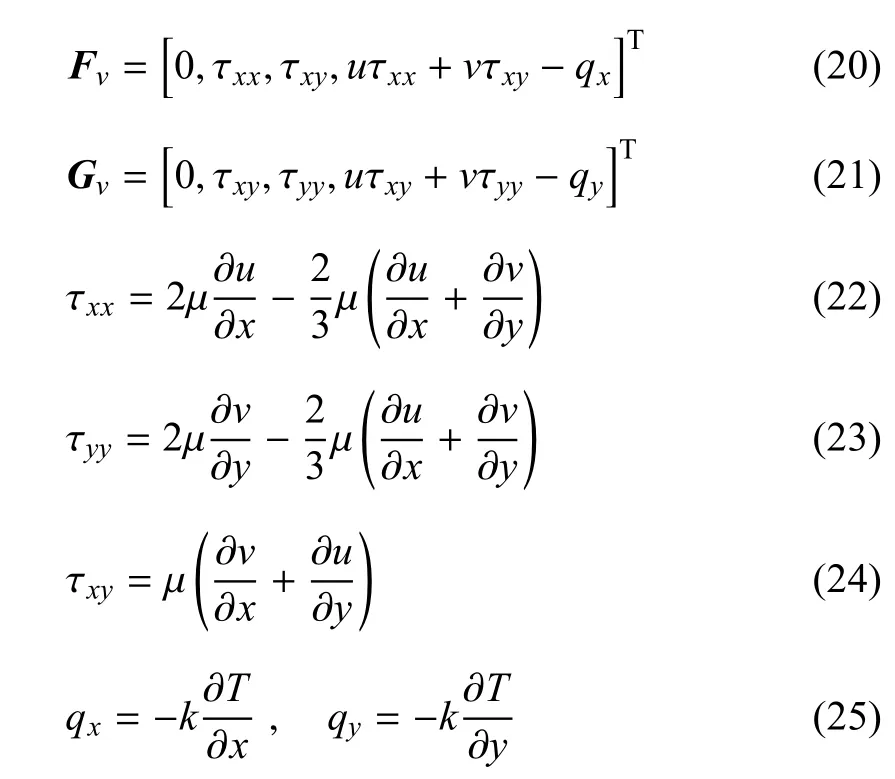
其中对于内能e，完全气体采用式(1)，而振动激发采用式(5).黏性系数µ随温度T变化的近似关系由Sutherland公式给出，而热传导系数k则由普朗特数Pr给出[19]

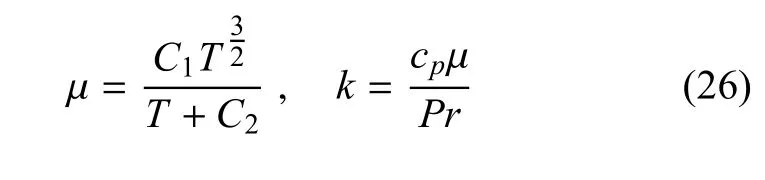
式中，C1=1.458×10-6，C2=110.4，Pr=0.72.

计算中采用有限差分方法、LUSGS隐式格式[20]进行求解.其中对无黏通量 F和 G的求解采用AUSMPW+格式[2122]，将流动通量分为对流项和压力项两部分，分别进行近似求解.该数值格式在高超声速流动的求解中，对激波和边界层的捕捉均表现出较好的性能[2324].迎风格式基本上是一阶的，为了取得更好的空间精度，采用MUSCL格式[25]对原始变量进行重构，并引入Van Albada限制器来限制重构时产生过大或过小的梯度

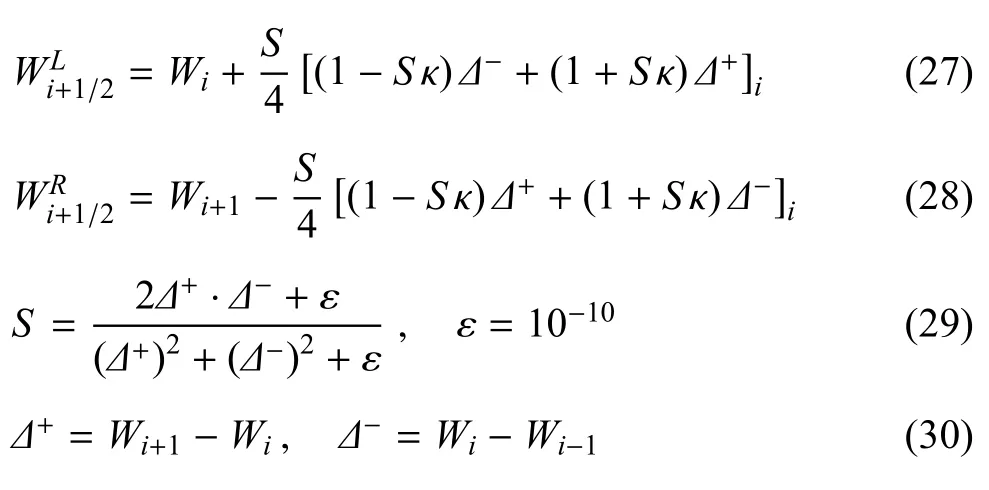
其中，W是原始变量.当κ=1/3时，该方法具有三阶空间精度[26].

对于平板边界层问题，计算域和网格示意图如图3.其中总网格数为858×812≈7.0×105，边界层第一层网格间距为5µm.壁面边界条件为等温壁，Tw=1500K.

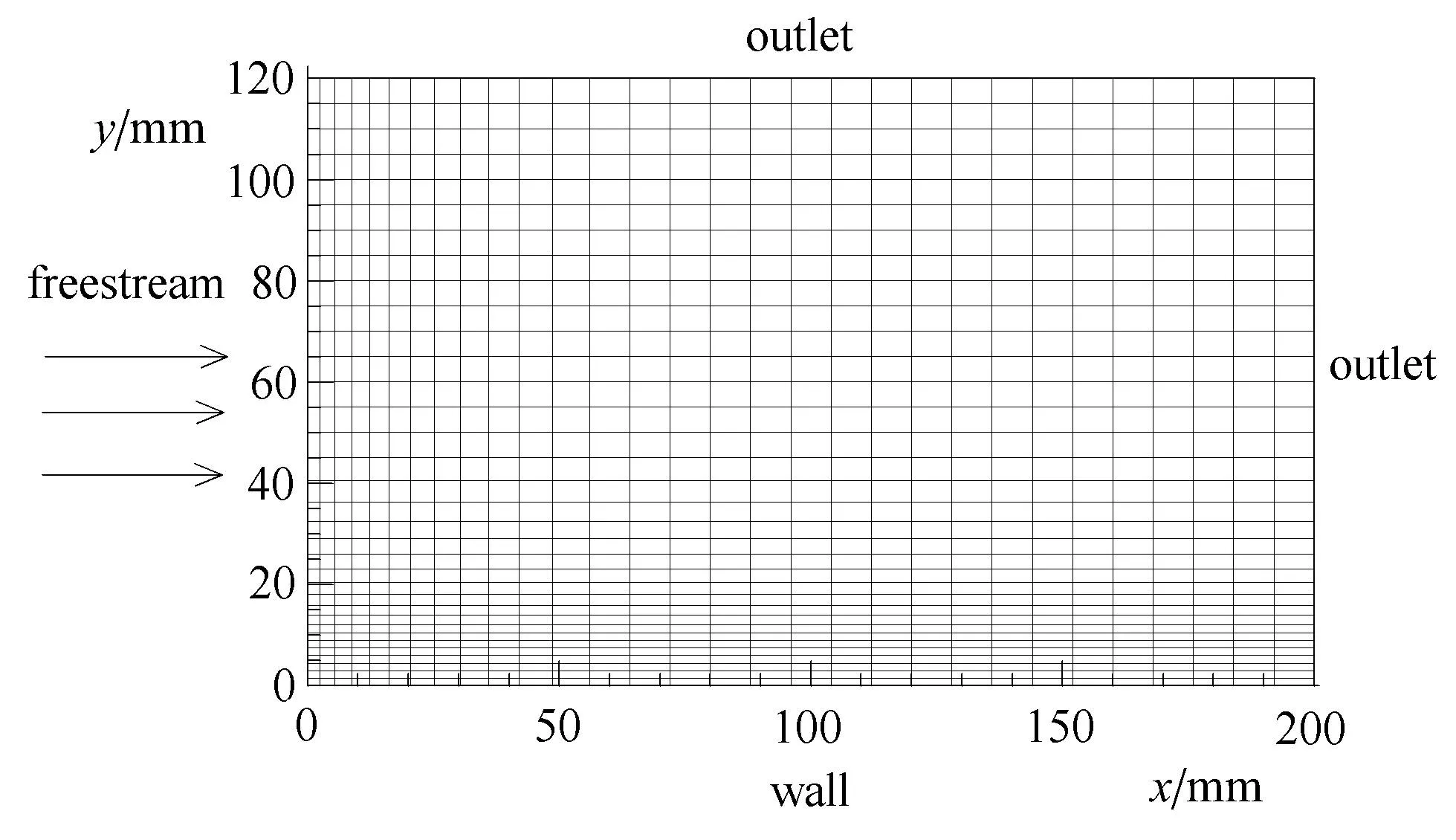
图3 计算域和网格示意图Fig.3 Computational domain and grids

2 结果与讨论

2.1 振动激发对斜激波的影响

这里采用1.3节提出的牛顿迭代公式分别对完全气体和考虑振动激发的斜激波关系进行精确求解，以分析振动激发对斜激波波后流场的定量影响.计算时，来流采用40km高空空气参数(T=250K，p=287Pa)，楔面角为 30◦.

图4给出了来流马赫数从6增大到12时，斜激波后的温度、压力、密度、速度、马赫数和激波角的变化.从图中可以看出，与完全气体相比，考虑振动激发后斜激波波后温度降低、压力变小、密度变大、速度和马赫数变大、激波角变小.且随着来流马赫数的增大，激波压缩增强，波后温度增大，振动激发变得越来越显著，斜激波波后流场参数的偏差也越来越大.事实上，其他使斜激波波后温度增大的过程，如升高来流温度或增大楔面角，都会使振动激发变得显著，进而导致振动激发对斜激波的影响变大.

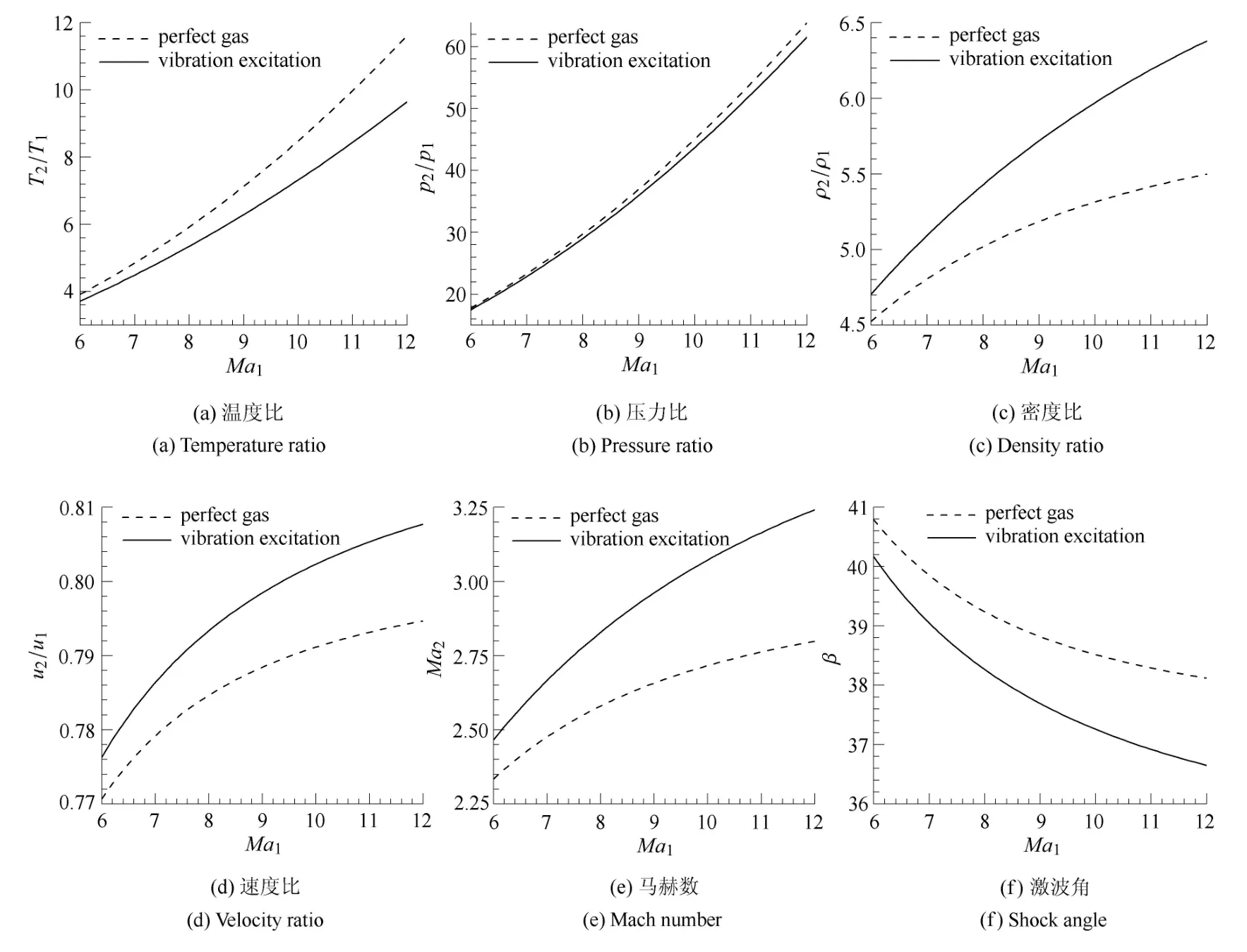
图4 斜激波前后流场参数Fig.4 Flow fiel parameters across oblique shock

取Ma=10的斜激波关系如表1所示.可见，振动激发对斜激波波后温度、密度、马赫数和激波角的影响较大，超过12%；而对波后压力和速度的影响较小，在4%以内.事实上，考虑振动激发后，斜激波波后气体能量有较大一部分转化成气体分子的振动能，使得气体分子平动能和转动能显著变小，于是作为表征分子平动能的温度比完全气体的相应值要小得多.这是振动激发对流场最直接的影响.温度显著变小，则声速也将显著变小，由于速度基本保持不变，导致波后马赫数显著变大.另外，由于压力变化不大，从状态方程可得密度将显著变大.

表1 Ma=10斜激波关系Table 1 Oblique shock properties at Ma=10

注意到，考虑振动激发后，斜激波波后流动的单位雷诺数Rex变化明显，达到23.65%.雷诺数的增大会导致边界层厚度减小，结合多个物理量的变化，如速度和温度，将共同对边界层内的摩擦阻力和气动热产生一定影响.由式(26)可知，温度显著降低将导致黏性系数µ显著变小，且由于密度显著变大，则式(31)给出的单位雷诺数Rex显著变大.

振动激发对斜激波波后流场参数产生显著影响，该流场又作为边界层的外流，将与振动激发对边界层流动的影响进行耦合，共同对边界层内流场产生影响，最终影响壁面处的气动特性.

2.2 振动激发对边界层的影响

这里分析边界层外流取斜激波波后流场参数时，振动激发对边界层流动的影响.采用1.4节中的数值方法求解平板边界层问题，即可得到边界层内流场以及壁面热流和摩阻.

当将斜激波波后流场取为边界层外流时，由表1可知，完全气体与考虑振动激发的流场温度差异很大，从而声速差异很大，马赫数差异也很大.即在高温气体效应显著时，采用速度描述流动比马赫数更准确.另外，与边界层内壁面摩阻直接相关的是速度而不是马赫数.因此，在本小节采用速度替代马赫数来描述流动.斜激波前自由来流为U=3176m/s(Ma=10),T=250K,p=287Pa,θ=30◦时，完全气体或考虑振动激发，斜激波波后流场参数约为U=2530m/s,T=2000K,p=12750Pa.

2.2.1 对边界层流场参数的影响

取U=2530m/s,T=2000K,p=12750Pa为边界层外流，壁面温度为Tw=1500K，此时平板边界层流场的温度云图如图5所示.距离平板前缘x=150mm处，完全气体或考虑振动激发的温度边界层及速度边界层的对比如图6.该位置的边界层厚度及与壁面热流、摩阻相关的参数汇总如表2和表3所示.其中速度边界层厚度δ、壁面热流qw和壁面摩阻τw分别按式(32)和式(33)定义为

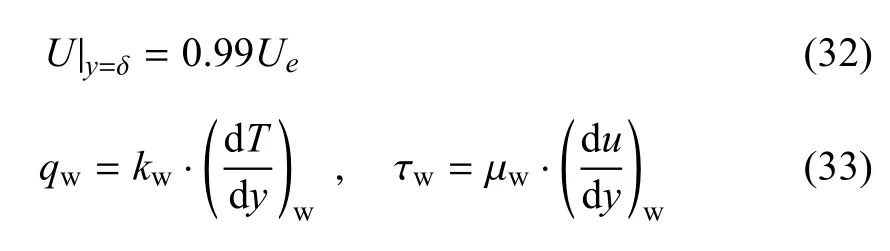
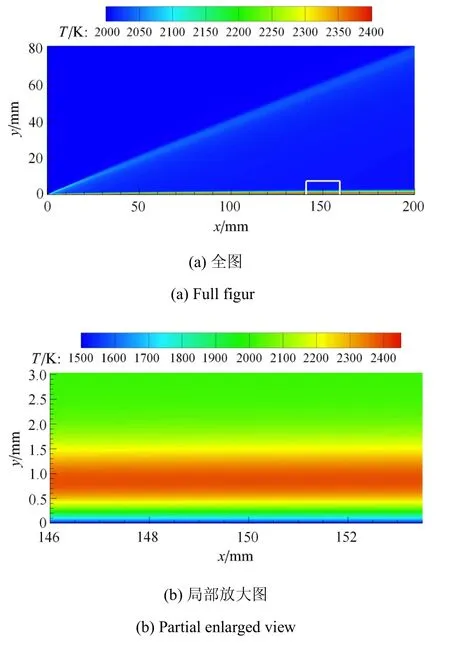
图5 平板边界层(完全气体)流场温度云图Fig.5 Temperature contour of flat-plat boundary layer of perfect gas

从图6和表2可见，与完全气体对比，考虑振动激发后，边界层内最高温度 Tmax下降明显，从2390K降低到2278K，降低了4.69%.而边界层内最高温度所在位置y|Tmax变化较小.由此可得，振动激发使壁面温度梯度显著降低，计算结果给出变化为-13.11%.然而壁面是等温壁，Tw=1500K，由式(9)可得，壁面处的比定压热容cp|w考虑振动激发后多出与分子振动能相关的项，从而显著增大.而黏性系数仅与温度有关，等温壁处的黏性系数µw保持不变.因此，由式(26)可得壁面处的热传导系数kw显著增大，变化为20.18%.根据壁面热流的定义式(33)，壁面热流qw的变化为

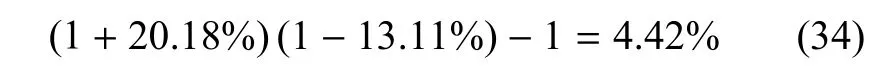
从图6和表3可知，与完全气体对比，考虑振动激发后，速度边界层厚度稍微减小，减小了2.82%.在外流速度相同时，壁面速度梯度也稍微增大，变化为0.95%.另外，等温壁的黏性系数µw保持不变.因此，根据壁面摩阻的定义式(33)，壁面摩阻τw与壁面速度梯度的变化趋势相同，也有0.95%的小变化.

综上，在边界层外流条件相同时，振动激发对边界层内流动以及壁面热流、摩阻都产生一定影响.

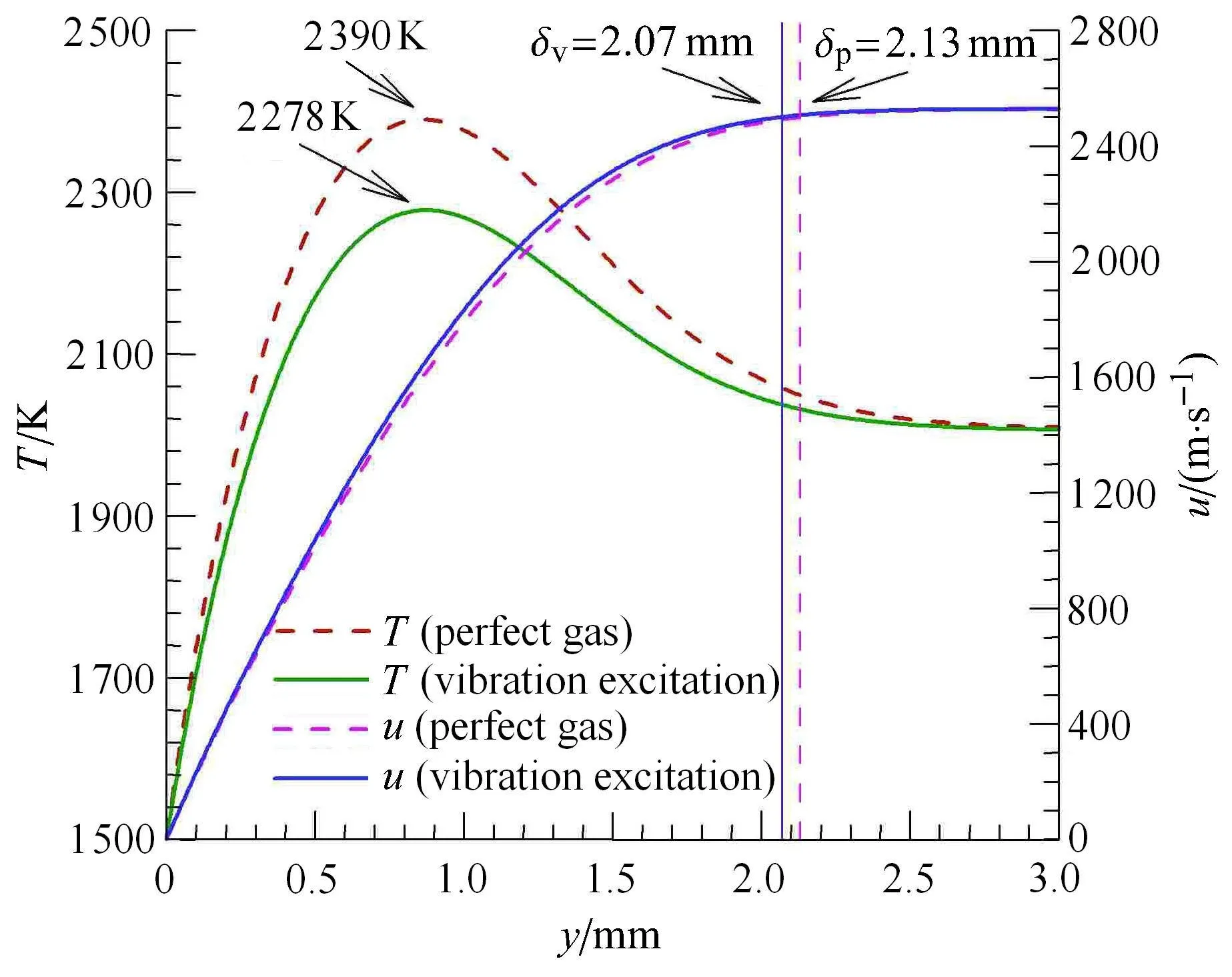
图6 边界层的温度和速度剖面(x=150mm)Fig.6 Profile of temperature and velocity in boundary layer at x=150mm

表2 壁面温度梯度与热流(x=150mm)Table 2 Temperature gradient and heat flu at wall of x=150mm

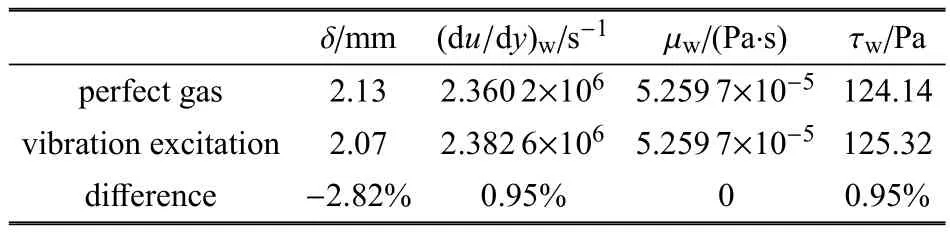
表3 壁面速度梯度与摩阻(x=150mm)Table 3 Velocity gradient and friction at wall of x=150mm

2.2.2 随外流参数的变化规律

边界层内流动和壁面热流、摩阻主要受外流速度 U、温度 T以及压力 p的共同影响.在 U =2530m/s,T=2000K,p=12750Pa条件下，固定其中两个，改变另一个，可以得到完全气体或考虑振动激发的壁面热流qw、摩阻τw以及振动激发对其影响大小随外流参数的变化规律，如图7.其中，分别按式(35)和式(36)将振动激发对壁面热流和摩阻的影响定义成两个物理量：δqw和δτw.

由图7可见，壁面热流qw对外流速度U、温度T、压力p都比较敏感，而壁面摩阻τw对外流速度U和压力p比较敏感，外流温度T对τw影响较小.壁面热流qw、摩阻τw随外流速度U、温度T和压力p而变化说明，斜激波波后流动作为边界层外流，在振动激发使斜激波波后流场参数发生变化时，最终通过边界层的传递作用，会对壁面热流和摩阻产生影响.

从图7还可得到，振动激发的影响大小δqw和δτw也会随外流速度U和外流温度T而变化.这又说明，边界层的存在不仅传递振动激发对外流产生的影响，还将其与振动激发对自身的影响进行耦合，使振动激发对气动力/热特性的影响机理变得复杂.其中从图7(a)和图7(b)可得，δqw随U,T变化较大，即振动激发通过斜激波使边界层外流发生变化时，会极大地干扰振动激发通过改变边界层内流动而对壁面热流qw产生的影响大小.这说明，振动激发通过在斜激波中改变边界层外流而对qw产生的影响与通过改变边界层内流动而对qw产生的影响是强烈耦合在一起的，不是简单的叠加.

从图7(d)和图7(e)可得，δτw随U,T变化相对较小，即在振动激发通过斜激波使边界层外流发生变化时，振动激发通过改变边界层内流动而对壁面摩阻τw产生的影响大小相对较稳定，所受干扰较小.这说明，振动激发通过在斜激波中改变边界层外流而对τw产生的影响，与通过改变边界层内流动而对τw产生的影响的耦合作用较弱，基本是解耦的.

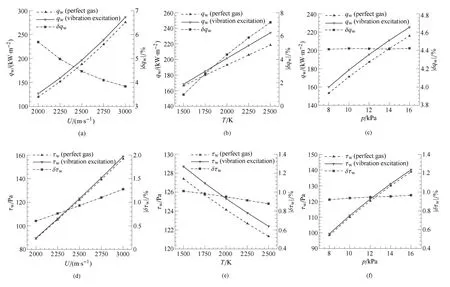
图7 qw,|δqw|,τw,|δτw|随 U,T,p 的变化Fig.7 Variation of qw,|δqw|,τw,|δτw|as functions of U,T,p

2.3 综合分析

2.3.1 渐进求解的结果

为了分析斜激波和边界层同时考虑振动激发时对壁面压力、摩阻和热流的影响，这里选择速度U=3176m/s(Ma=10)、温度T=250K、压力p=287Pa的空气流过角度θ=30◦,长度L=20cm的斜劈作为实例，采用1.2节中提出的渐进分析方法分两步求解.分析结果如图8，图中点标志X-X(X=P,R)中，第1个字母表示斜激波的计算模型，第2个字母表示边界层的计算模型，P表示完全气体模型，R表示考虑振动激发的热完全气体模型，两点之间连线上的百分比代表的是两者的差别大小.

由图8(a)可见，振动激发对壁面压力系数的影响基本上是通过改变斜激波波后压力实现的，边界层的作用较小，符合边界层理论.

从图8(b)可见，斜激波或边界层单独考虑振动激发时，都会使壁面摩阻τw增大，分别为1.85%和0.92%，斜激波的影响较大.注意到，P-P,R-P,P-R,R-R四个点组成的图形非常接近平行四边形.这说明斜激波考虑振动激发时对壁面摩阻τw产生的影响与边界层考虑振动激发产生的影响近似可以叠加，叠加结果为：1.85%+0.92%=2.77%，与斜激波和边界层同时考虑振动激发时的结果(2.85%)非常接近.即振动激发通过在斜激波中改变边界层外流而对τw产生的影响，与通过改变边界层内流动而对τw产生的影响的耦合作用较弱，基本是解耦的.2.2.2节中指出，这是因为振动激发通过改变边界层内流动而对壁面摩阻τw产生的影响大小相对较稳定，受边界层外流参数变化的干扰较小，即受振动激发对斜激波影响的干扰较小.

由图8(c)可见，斜激波考虑振动激发时会使壁面热流qw减小，影响为-6.51%.而边界层考虑振动激发时会使壁面热流qw增大，影响为5.18%.即在斜激波或边界层这两种流场结构中，振动激发对壁面热流qw的影响方向是相反的，当斜激波和边界层同时考虑振动激发时，两者的作用会发生一定的抵消，最终削弱了振动激发对壁面热流qw产生的影响(-3.46%).注意到，与壁面摩阻的结果不同的是，P-P,R-P,P-R,R-R四个点组成的图形与平行四边形(图中虚线)差异较大.当将斜激波考虑振动激发时对壁面热流qw产生的影响与边界层考虑振动激发产生的影响进行叠加，结果为：-6.51%+5.18%=-1.33%，图中(+)点.对比斜激波和边界层同时考虑振动激发时的结果(-3.46%)，差异较大，相差-1.33%-(-3.46%)=2.13%.这说明振动激发通过在斜激波中改变边界层外流而对qw产生的影响与通过改变边界层内流动而对qw产生的影响是强烈耦合在一起的，不能简单叠加.2.2.2节中指出，这是因为在振动激发通过斜激波使边界层外流发生变化时，会极大地干扰振动激发通过改变边界层内流动而对壁面热流qw产生的影响大小.

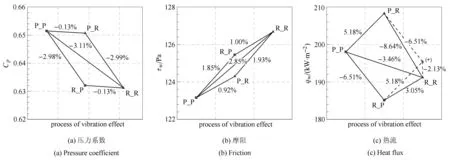
图8 振动激发对气动力/热特性影响的路径图Fig.8 Paths of vibration e ff ects on aerodynamic and aerothermodynamic characteristics

2.3.2 直接求解的结果

为了验证以上两步渐进分析方法的合理性，对同样的高超声速黏性斜劈问题采用1.4节中给出的数值方法进行直接求解.图9是完全气体和考虑振动激发的斜劈流场温度云图的对比图.从图中可见，考虑振动激发斜激波波后温度从完全气体的2143K降低到1844K，变化显著.另外，与完全气体进行对比，考虑振动激发后激波层厚度明显变薄，激波角明显变小.这些变化规律与2.1节的结果吻合.

距离斜劈前缘x=150mm处，完全气体和考虑振动激发两种气体模型的壁面压力系数Cp、摩阻τw和热流 qw的计算结果如表 4.可见，对比完全气体的结果，考虑振动激发后壁面压力系数Cp变化-3.08%，摩阻变化3.45%，热流变化-3.09%.将该结果与图8给出的结果对比发现，渐进求解得到的振动激发对高超声速气动力/热特性的影响大小与该直接求解得到的结果非常接近，误差较小.这说明以上提出的两步渐进分析方法及其结果是合理的，且该方法对在斜激波与边界层组合结构中分析振动激发对壁面摩阻、热流的影响规律以及估计其影响大小具有很大的工程应用价值.

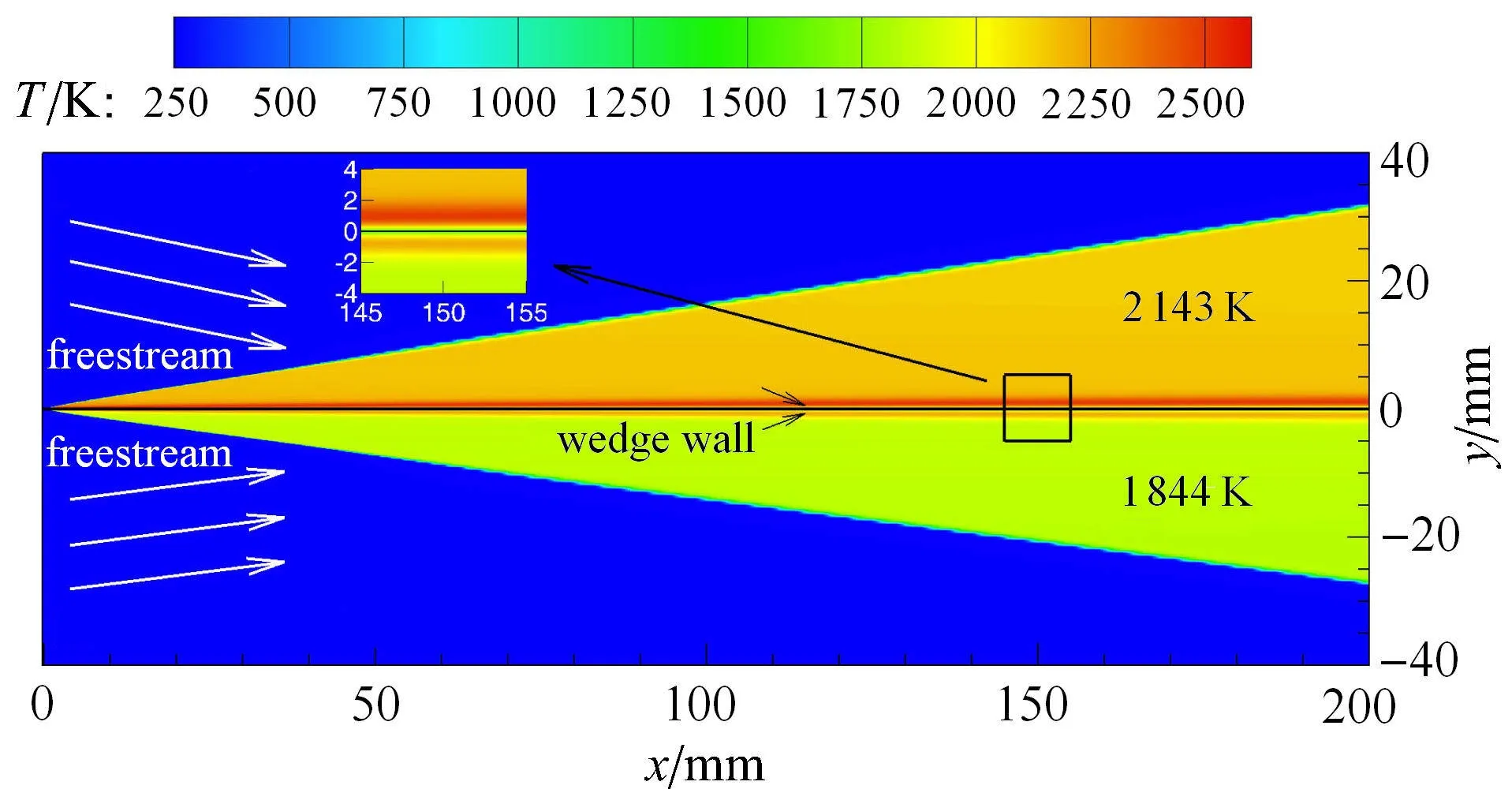
图9 完全气体(a)和考虑振动激发(b)的斜劈流场温度云图的对比图Fig.9 Comparison of temperature contour of wedge of perfect gas(a)and vibration excitation(b)

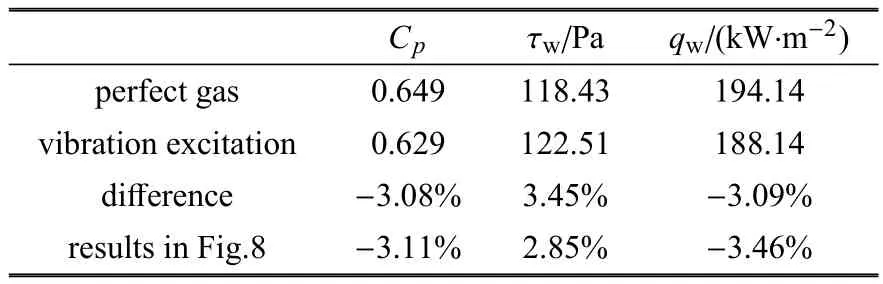
表4 斜劈的气动力/热特性(x=150mm)Table 4 Aerodynamic and aerothermodynamic characteristics of wedge at x=150mm

3 结论

高超声速气流通过斜激波与边界层的加热诱导空气分子振动激发，从而影响飞行器表面的气动力/热特性.本文新提出一种理论求解斜激波与数值求解边界层相结合的两步渐进方法，研究了振动激发过程对二维斜劈的气动力/热特性的影响规律，并分析了振动激发效应在激波层与边界层内的传递和干扰机理.

研究结果表明，对比完全气体，振动激发使壁面摩阻升高，使壁面热流降低.在斜激波中，振动激发使波后温度、压力降低，密度、速度、马赫数升高，激波角减小，单位雷诺数增大.其中，振动激发对斜激波波后温度、密度、马赫数、激波角和单位雷诺数的影响较大.发生振动激发后，斜激波波后雷诺数的增大会导致边界层厚度减小，结合多个物理量的变化，如速度和温度，共同对边界层内的摩擦阻力和气动热产生影响.在边界层流动中，壁面热流、摩阻随外流速度、温度和压力而变化，表明边界层的存在会传递斜激波的振动激发效应而对壁面热流和摩阻产生影响.另外，振动激发对壁面热流、摩阻的影响大小也随外流速度和温度而变化，说明边界层内的振动激发效应会与斜激波的振动激发效应发生相互干扰.采用渐进方法分析发现，振动激发通过在斜激波中改变边界层外流而对壁面热流产生的影响与通过改变边界层内流动而产生的影响是强烈耦合的，不能简单叠加.而在对壁面摩阻的影响中，耦合作用较弱，基本是解耦的.对高超声速黏性斜劈问题的直接求解结果验证了提出的两步渐进分析方法的合理性.

1姜宗林.触摸高温气体动力学.力学与实践,2006,28(5)：1-7(Jiang Zonglin.Feeling high temperature gas dynamics.Mechanics in Engineering,2006,28(5)：1-7(in Chinese))

2樊菁.高超声速高温气体效应判据.力学学报,2010,42(4)：591-596(Fan Jing.Criteria on high-temperature gas e ff ects around hypersonic vehicles.Chinese Journal of Theoretical and Applied Mechanics,2010,42(4)：591-596(in Chinese))

3 Anderson JD.Hypersonic and High-Temperature Gas Dynamics,2nd Edition.AIAA,2006

4童秉纲,孔祥言,邓国华.气体动力学.第2版.北京：高等教育出版社,2012(Tong Binggang,Kong Xiangyan,Deng Guohua.Gas Dynamics.2nd Edition.Beijing：Higher Education Press,2012(in Chinese))

5 Hirschel EH,Weiland C.Selected Aerothermodynamic Design Problems of Hypersonic Flight Vehicles.Berlin：Springer,2009

6 Compton HR,Schiess JR,Suit WT,et al.Stability and control over the supersonic and hypersonic speed range.Conference Paper,NASA Langley,1983

7 Brauckmann GJ,Paulson JW.Experimental and computational analysis of shuttle orbiter hypersonic trim anomaly.Journal of Spacecraft and Rockets,1995,32(5)：758-764

8 Muylaert J,Walpot L,Rostand P,et al.Extrapolation from wind tunnel to flight shuttle orbiter aerodynamics.Technical Report,NASA Langley,1998

9 Griffith BJ,Maus JR,Best JT.Explanation of the hypersonic longitudinal stability problem：lessons learned.NASA,1983

10 Romere PO,Young JC.Space shuttle entry longitudinal aerodynamic comparisons of fligh 2 with prefligh predictions.Journal of Spacecraft and Rockets,1983,20(6)：518-523

11 Calloway RL.Real-gas simulation for the shuttle orbiter and planetary entry configuration including fligh results.AIAA,1984

12 Jiang ZL,Yu HR.Experimental and development of the longtest-duration hypervelocity detonation-driven shock tunnel(LHDst).AIAA,2014

13姜宗林,李进平,赵伟等.长试验时间爆轰驱动激波风洞技术研究.力学学报,2012,44(5)：824-831(Jiang Zonglin,Li Jinping,Zhao Wei,et al.Investigating into techniques for extending the test-duration of detonation-driven shock tunnels.Chinese Journal of Theoretical and Applied Mechanics,2012,44(5)：824-831(in Chinese))

14刘云峰,汪运鹏,苑朝凯等.复现高超声速飞行条件下10◦尖锥标模气动力特性试验研究.中国力学大会,上海,2015(Liu Yunfeng,Wang Yunpeng,Yuan Chaokai,et al.Aerodynamic force and moment characteristics of 10 degree sharp cone at Mach 7.0 in JF12 shock tunnel.The Chinese Congress of Theoretical and Applied Mechanics,Shanghai,2015(in Chinese))

15汪运鹏,刘云峰,苑朝凯等.长试验时间激波风洞测力技术研究.力学学报,2016,48(3)：545-556(Wang Yunpeng,Liu Yunfeng,Yuan Chaokai,et al.Study on force measurement in long-test duration shock tunnel.Chinese Journal of Theoretical and Applied Mechanics,2016,48(3)：545-556(in Chinese))

16汪志诚.热力学·统计物理.第4版.北京：高等教育出版社,2008(Wang Zhicheng.Thermodynamics&Statistical Physics.4th Edition.Beijing：Higher Education Press,2008(in Chinese))

17张德良.计算流体力学教程.北京：高等教育出版社,2010(Zhang Deliang.A Course in Computational Fluid Dynamics.Beijing：Higher Education Press,2010(in Chinese))

18任玉新,陈海昕.计算流体力学基础.北京：清华大学出版社,2006(Ren Yuxin,Chen Haixin.Fundamentals of Computational Fluid Dynamics.Beijing：Tsinghua University Press,2006(in Chinese))

19卞荫贵,徐立功.气动热力学.第2版.合肥：中国科学技术大学出版社,2010(Bian Yingui,Xu Ligong.Aerothermodynamics.2nd Edition.Hefei：University of Science and Technology of China Press,2010(in Chinese))

20 Seokkwan Y,Antony J.Lower-upper symmetric-gauss-seidel method for the Euler and Navier-Stokes equations.AIAA Journal,1988,26(9)：1025-1026

21 KimKH,KimC,RhoOH.Methodsfortheaccuratecomputationsof hypersonic fl ws I.AUSMPW+scheme.Journal of ComputationalPhysics,2001,174(1)：38-80

22 Kim KH,Lee JH,Rho OH.An improvement of AUSM schemes by introducing the pressure-based weight functions.Computers&Fluids,1988,27(3)：311-346

23 Keiichi K,Eiji S,Yoshiaki N,et al.Evaluation of Euler flu for hypersonic heating computations.AIAA Journal,2010,48(4)：763-776

24 Ren Yuxin.A robust shock-capturing scheme based on rotated Riemann solvers.Computers&Fluid,2003,32(10)：1379-1403

25 Van Leer B.Towards to the ultimate conservation di ff erence schemes：V.a second-order sequel to Godunov method.Journal of Computational Physics,1979,32(1)：101-136

26 Collela P.A direct Eulerian MUSCL scheme for gas dynamics.SIAM Journal on Scientifi and Statistical Computing,1985,6(1)：104-117

EFFECT OF VIBRATION EXCITATION ON HYPERSONIC AERODYNAMIC AND AEROTHERMODYNAMIC1)

Zhang Zijian2)Liu Yunfeng Jiang Zonglin
(State Key Laboratory of High-Temperature Gas Dynamics，Institute of Mechanics，CAS，Beijing 100190，China)(University of Chinese Academy of Sciences，Beijing 100049，China)

With the increasing of fligh Mach number,the high-temperature gas e ff ect of air has becoming remarkable,which has significan impacts on the aerodynamics and aerothermodynamic characteristics of hypersonic vehicles.Because of the complex mechanism and numerous key parameters of high-temperature gas e ff ect,it has not been fully studied at home and abroad.When the high-temperature gas e ff ect occurs,multiple nonlinear physical processes are coupled together.However,ground tests and numerical simulations can not decouple these processes and can not explain the key physical mechanisms.To solve this problem,a new two-step asymptotic approximation method combining theoretic analysis and numerical simulation is proposed.In this method,the oblique shock relation with vibration excitation e ff ect is obtained by Newton iterative method,then the results are used as the boundary conditions of the boundary layer andit is solved numerically.By using this method,the e ff ect of vibration excitation on the aerodynamics and aerothermodynamic characteristics of a two dimensional wedge is studied.The results show that,the vibration excitation process has great e ff ect on the shock angle,the temperature,density,Mach number,and Reynolds number behind the oblique shock,but little influenc on the pressure and velocity.The inviscid fl w behind the oblique shock is coupled together with the boundary layer fl w.The changes of multiple physical quantities,including the increase of velocity and the decrease of the temperature behind the oblique shock,and the decrease of the boundary layer thickness due to the increase of the Reynolds number,have an e ff ect on the friction and aerodynamic heating in the boundary layer.Comparing with perfect gas model,vibration excitation increases the wall friction and decreases the wall heat flu of the wedge.By influencin the shock layer and the boundary layer respectively,the e ff ects of vibration excitation on heat flu are strong coupled,while they are weak coupled on friction.

vibration excitation，aerodynamic and aerothermodynamic，boundary layer，high-temperature gas e ff ect

V211.22

：A

10.6052/0459-1879-16-307

2016–11–02 收稿，2017–01–24 录用,2017–01–24 网络版发表.

1)国家自然科学基金资助项目(11672312，11532014).

2)张子健，博士研究生，主要研究方向：高温气体动力学.E-mail：zhangzijian@imech.ac.cn

张子健，刘云峰，姜宗林，振动激发对高超声速气动力/热影响.力学学报,2017,49(3)：616-626

Zhang Zijian,Liu Yunfeng,Jiang Zonglin.E ff ect of vibration excitation on hypersonic aerodynamic and aerothermodynamic.Chinese Journal of Theoretical and Applied Mechanics,2017,49(3)：616-626