非线性被动隔振的若干进展1)

陆泽琦 陈立群 ,†,2)

∗(上海大学上海市应用数学和力学研究所，上海200072)†(上海大学力学系，上海200444)

非线性被动隔振的若干进展1)

陆泽琦∗陈立群∗,†,2)

∗(上海大学上海市应用数学和力学研究所，上海200072)†(上海大学力学系，上海200444)

工程中航空航天、船舶与海洋结构物及其上装备和精密仪器易受极端环境干扰和破坏，使得非线性隔振理论在近十年来迅猛发展；针对日益严峻的隔振和抗冲击等要求，工程师和科学家们已发展出各种不同的非线性隔振系统，包括主动、半主动、被动和复合隔振.利用非线性改善的被动隔振兼具传统被动隔振的鲁棒性和主动隔振的高效性成为振动控制领域的先进技术.本文主要综述了非线性隔振理论和应用的近十年进展，包括非线性隔振设计、建模、分析、仿真和实验.在隔振系统的构建中，既考虑了刚度非线性又考虑了阻尼非线性；动力学响应的研究中，既有确定性分析又有随机分析.首先提出了适用于非线性隔振系统改进的评价方式；其次综述了高静态低动态刚度隔振及其加强形式非线性阻尼加强和双层非线性隔振，混沌反控制技术、内共振影响、非线性能量阱应用等振动机制利用型隔振和非线性隔振功能材料.最后，对非线性隔振研究发展的热点和关键性问题进行了分析和展望.

隔振，非线性振动，高静态低动态刚度，非线性阻尼，隔振材料

引言

在绝大多数工程振动系统中，振动都被认为是有害的，机械振动会导致轴承磨损过大、紧固件松动、结构性或机构性失效和降低效率.很多方法可以用来减小传递到被激振结构的振动.理想的方法是设计低噪声机械设备，或者通过加入外部设备,比如动力吸振器来减少振动响应.其中在振源和接受结构之间引入隔振元件的方法是目前最为关注的振动控制方法，即通过改变传递途径的方式达到隔离振动的目的，如图1所示.

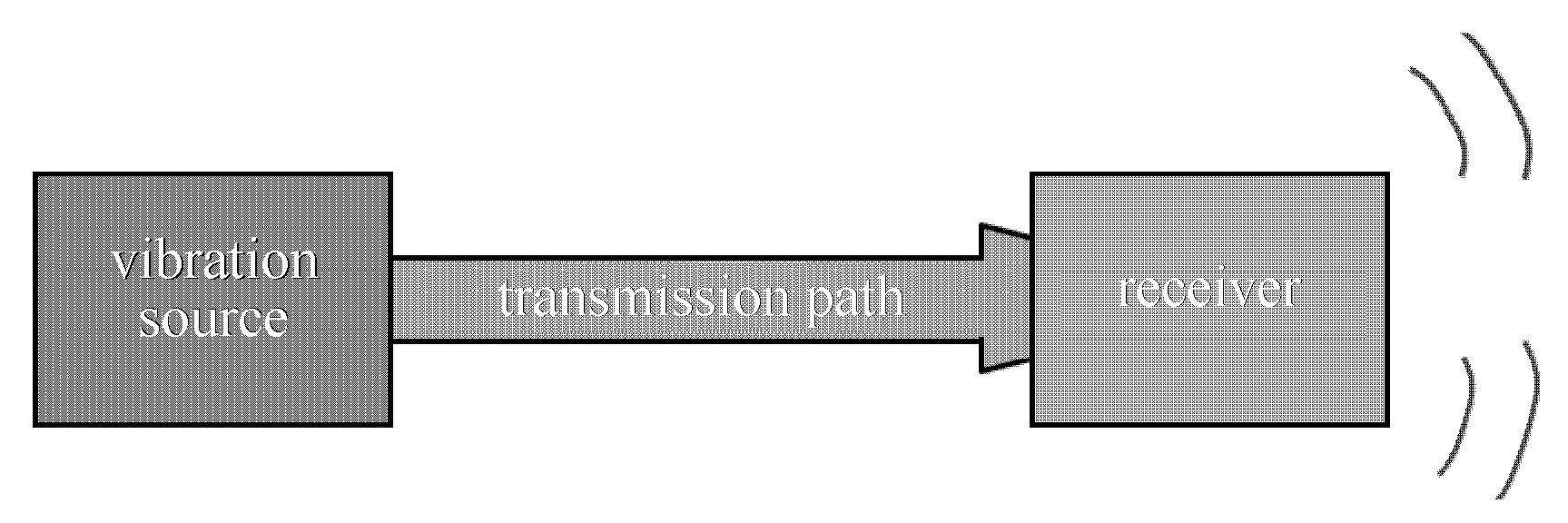
图1 隔振问题Fig.1 Schematic diagram of vibration isolation

被动隔振器是一个承载并且消耗能量的元件，它结构简单，不需要外部能量,并具一定经济性优势，因此在很多情况下成为解决工程振动传递问题的首选方案[1].Piersol[2]和Rivin[3]对被动隔振系统作了全面阐述和分析.但目前广泛使用的被动隔振存在两个自身的缺点：一方面，对于低频外扰的隔振,在实现时会遇到静变形过大和失稳的问题；另一方面，阻尼可以减少共振频率下的响应,但会降低隔振区的隔振效率.被动隔振对低频振动控制不足，可以通过主动隔振来克服，但主动控制技术结构复杂、能耗大、成本较高，并且存在作动器输出力与响应时间的限制、传感器探测的信号在测量和传输过程中的迟滞等问题[46].除了主动隔振以外，被动隔振的第一个缺点可以通过引入具有高静态、低动态刚度的非线性隔振元件来克服，这类系统是通过弹簧的特定几何构型来获得较低的动刚度和固有频率，同时具有较小的静态变形[7].第二个缺点可以通过非线性阻尼隔振克服，例如库伦阻尼、幂函数阻尼、平方/立方阻尼、迟滞阻尼[8]，从而实现在振动位移较大时(比如共振频率处)阻尼较大、在振动位移较小时(比如在高频处)阻尼也较小的目的.

环境激励导致结构振动隔离的复杂性.被保护结构服役期间通常会受到几类环境激励.这些激励通常是自然和动态的，会导致结构部件的振动和破坏[9-10]：

(1)引起船舶与海洋结构振动，如动态波浪、风、洋流、冰或地震等载荷[10];

(2)引起航天器微振动，如火箭发动机振动、太阳能帆板展开和收缩等冲击载荷、昼夜温差引起载荷、空间的不稳定辐射干扰等[9].

利用非线性以提高被动隔振系统的性能，是隔振领域一个重要的研究方向.特别是在过去十年间非线性隔振在工程各个领域得到广泛应用.但是除了2008年Ibriham发表相关综述[7]外，再没有新的文章总结在非线性隔振方面取得的最新成绩和进展.本文总结了非线性隔振近十年的研究成果，尤其是高静态低动态系统方面的成果，也包括作者的工作.

1 非线性隔振工程应用

1.1 航天器隔振

航天器结构在对接过程中会产生振动和冲击环境，另外在发射过程中火箭发动机推进不可能一直是稳定状态，发射过程中的振动也会对航天器结构造成影响，甚至其振动会对航天器结构的运行及稳定性产生致命影响[9,11].因此航天器结构振动控制对其操作性和稳定性有重要意义，减振设计已成为航天器平台设计的重要内容之一.事实上，由于航天器结构应用环境的特殊性及其振动精度要求的极端重要性，在应用振动控制技术解决航天器振动控制和结构探测问题时，相当一部分工程问题受到实际条件的制约，由此引出诸多技术难题，形成了当前航天器结构振动控制技术前沿的重要组成部分[12].Zheng等[13]针对整星结构提出Octo-strut主被动一体化非线性隔振平台，其原理是应用气动主、被动一体化技术实现结构的振动抑制.Zhang等[1419]研究了星上扰振部件与隔振系统的耦合问题，提出被动隔振装置参数设计方法，以及振动抑制和姿态控制联合方法，提高了高精度、高稳定度航天器的姿态快速机动与快速稳定的能力.

1.2 船舶与海洋结构物隔振

各种环境激励引起海洋结构振动，降低了海洋平台的生产能力和安全性，影响了海洋结构物的操纵性；在过去几十年里已成为船舶与海洋工程结构的事故和破坏的主要因数[2022].由于自激的非线性水动力、大变形和强非线性响应，船舶与海洋工程振动控制已成为新的挑战.一般振动控制策略已得到广泛研究并认为能有效缓解结构振动，但强调特定方法的船舶与海洋工程结构振动设计存在局限性.Kandasamy等[10]综述了振动控制方法以及在船舶与海洋工程中的应用；被动、主动、半主动和复合控制的各种传统策略和方法以及针对船舶与海洋工程结构振动控制方法.船舶与海洋工程振动控制结构包括夹套结构[23]、张力腿平台[24]、柱状支撑结构、浮式生产储油轮、卸油轮和立管结构[25].

2 非线性隔振效果评估

2.1 非线性振动传递率

振动传递率是评价隔振系统效能的关键参数.线性系统力传递率定义为传递力(ft)与激励力(fe)的幅值比；位移传递率定义为被保护结构位移(xt)与基础位移(xe)的幅值比.线性系统力和位移传递率的数学表达式是相同的，表示为

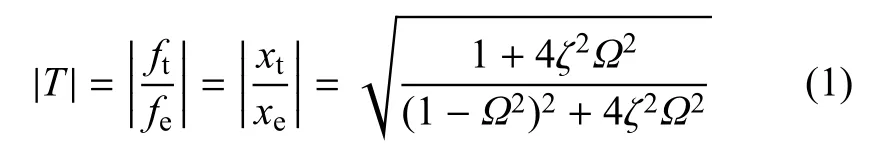
其中，ζ为阻尼比，Ω为无量纲激励频率.而非线性系统在谐波激励下，力和位移响应存在除基础频率以外的频率成分.它可能是周期、准周期或混沌响应.因此幅值比用于定义传递率存在局限性.Lu等[26]提出了响应与激励的均方根值之比作为传递率的定义

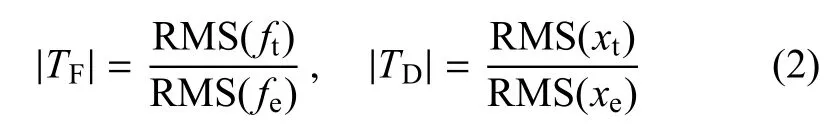
改进的定义有利于保能，因为通过均方根值可以计及响应的其他频率成分，这将减少能量在定义时的损失.Lu等[26]对双层非线性隔振系统展开传递率定义的适用性研究，用近似方法和数值方法定量研究高阶谐波对传递率的影响.最后改进的传递率推广到准周期、混沌响应.

2.2 功率流指标

在很多情况下隔振基础具有柔性特征，隔振器和基础之间存在强烈的耦合效应.刚性基础假设的系统建模忽略了振源和基础间耦合，导致以往研究不够精准[27-28].

功率流分析考虑了力、速度和它们之间的相位关系；作为一个独立描述系统响应的参数，用来评价隔振，可以得到更丰富的动力学特性[29].因此，研究非线性隔振系统功率流很必要.马业忠等[30]将柔性基础简化为矩形薄板，运用谐波平衡和Newton迭代法研究非线性刚度和阻尼对隔振系统功率流的影响.高书磊等[31]将柔性基础看作柔性梁，用功率流评价隔振效果，运用谐波平衡和Newton迭代法研究了系统参数对功率流的影响.Royston等[32]考察了通过非线性隔振器的功率流；建立了振源--非线性路径--接收结构的运动方程，运用谐波平衡结合弧长延伸算法研究了稳态响应，结构噪声产生于次噪声频率激励；基础模型为多自由度，振动谐次与接收结构频率相符，较高谐次会传递较高幅值振动.Xiong等[33]研究了非线性耦合系统的功率流特征，这类系统包括机器、非线性隔振器和受海浪激励的柔性船；刚度和阻尼非线性度为p和q阶，运用谐波平衡法分析稳态响应，研究了由于海浪引起的振源对输入到整个系统功率流的影响.Kerschen等[34]运用功率流方法研究了非线性保守系统的非线性模态和频率能量依赖特点.Yang等[35]运用平均法研究了具有负刚度特征的隔振系统功率流特性.提出了非线性隔振系统优化设计以达到最小亚谐波共振.Yang等[36]研究了达芬振子功率流动力学行为，揭示了由于非线性引起的不同功率输入和耗散特性，运用谐波平衡和龙格库塔数值方法研究了平均输入功率；超/亚谐波周期响应能增加平均输入功率，输入功率幅值依赖于初始条件.Yang等[37]基于平均法比较了考虑非线性基础的非线性隔振器功率流和传递率，并得到数值验证.无论是渐软还是渐硬基础，渐软非线性隔振器优于渐硬隔振器.

3 高静态低动态刚度隔振

3.1 确定性分析

Ibrahim[7]对高静态低动态非线性刚度隔振做了综述，比较了许多不同非线性隔振器的优劣和发展，寻找高效紧凑的负刚度结构成为实现高静态低动态非线性刚度隔振的关键[3839].Robertson[40]等提出了磁悬浮隔振系统，通过磁铁布置产生负刚度来降低悬浮系统的固有频率，并讨论了磁铁作用面积和间隙对刚度曲线的影响，为研究磁铁型高静态低动态隔振系统提供了设计基础[41].彭超等[42]研制了一种新型高静态低动态刚度隔振系统，由3个特定形状的片弹簧对称分布构成，可显著降低系统起始隔振频率；建立了隔振实验平台，验证了理论结果.路纯红等[43]通过分析正负刚度并联机理，也设计了一种新型超低频被动隔振系统.Carrella等[44]研究了准零刚度(qausi zero sti ff ness,QZS)隔振系统，它是由一个竖直弹簧和两个水平弹簧(与传递振动的方向垂直的普通线性弹簧)组成，竖直弹簧作为静变形的支撑刚度，两个水平弹簧在平衡位置处预压产生负刚度，由三弹簧组成的隔振系统性能优于线性隔振系统，而且具有较低的静态变形，如图2所示.在竖直方向上作用力与产生位移间关系可写为

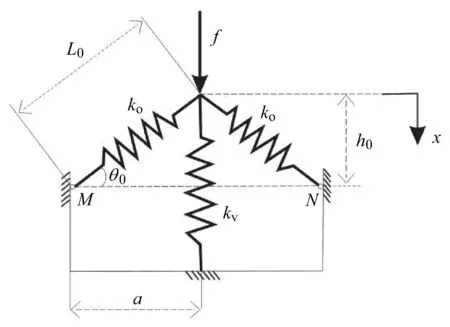
图2 准零刚度模型[44]Fig.2 QZS model[44]

Kovacic等[45]和Carrella等[4647]利用三弹簧结构建立了高静态低动态刚度隔振系统,如图3所示.水平放置的弹簧引入了几何非线性刚度，调节水平弹簧刚度以减少系统固有频率，隔振的频率范围往低频扩展.隔振器的受力--位移关系可以写成多项式形式

其中，k1=kv1-2(lo/l-1)kh1，k3=lo/l3kh1，lo是水平弹簧的初始长度，l是当它处于水平位置时的长度.当lo＞l时，水平弹簧kh1可以减小隔振系统线性刚度，让其小于线性刚度kv1，减小系统的固有频率，但同时引入立方刚度项.水平弹簧作用包括扩大隔振频率范围以及产生渐硬非线性，会导致潜在跳跃现象.

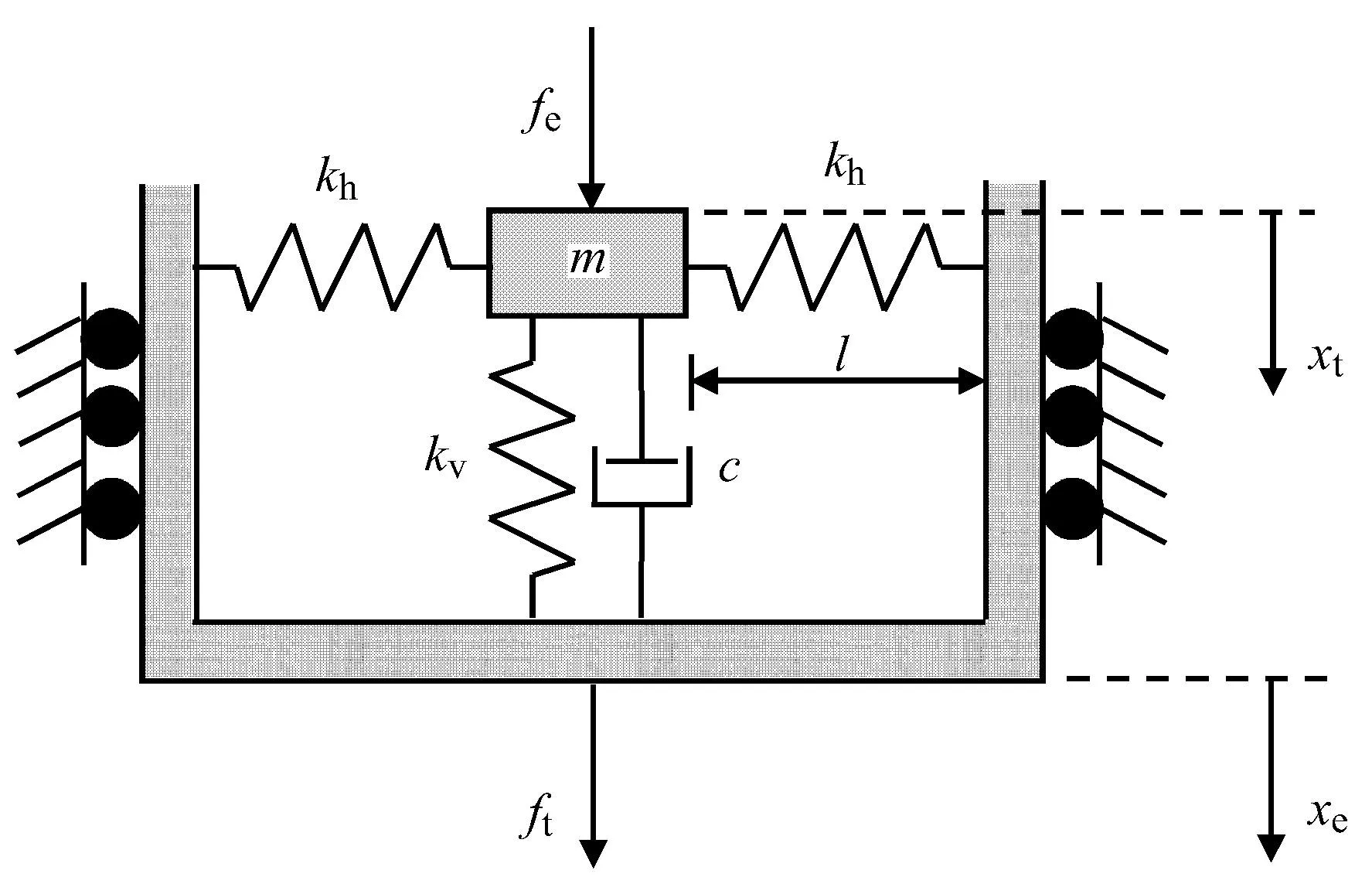
图3 高静态低动态隔振系统示意图[46]Fig.3 Schematic of nonlinear vibration isolation system with high-static-low-dynamic sti ff ness[46]

微振动时(x≤0.2l)，图3所示的非线性隔振系统运动方程可以近似并无量纲化为

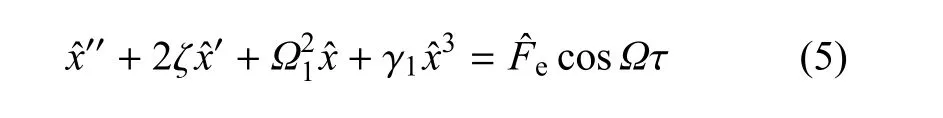
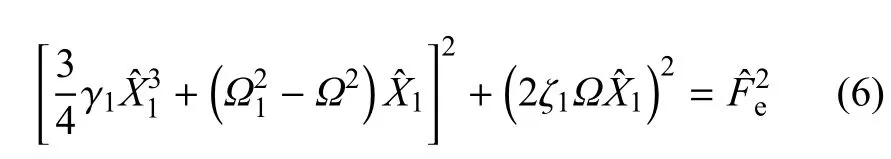
徐道临等[48]在磁力式QZS隔振系统中加入调节技术可以适应于不同加载质量.Sun等[49]在准零刚度隔振系统中加入时滞反馈的主动控制策略，时滞反馈控制不但提高了系统的鲁棒性，同时提高了隔振性能.Li等[50]提出了构建负刚度的有效方法，通过设计实验台实验研究了磁力式负刚度隔振器，磁弹簧和橡胶相耦合时产生较低固有频率和较大静载能力，固有频率可达到1.5Hz，在0～100Hz传递率最大下降40dB.Huang等[51]使用光滑梁作为负刚度设计了极低固有频率的隔振系统，隔振器刚度和外载缺陷会导致动力学响应呈现出渐软、渐硬和软硬共存特性，外载缺陷会使系统呈现渐软特性，增加刚度缺陷会弱化外载缺陷所引起的渐软特性，增加激励幅值会使隔振在不同的刚度特征间复杂转迁[52].引入剪刀形元件(scissor-like structure,SLS)作为产生几何非线性特性的构件开始受到关注[53]；Zhang等[54]分析和研究了SLS的非线性刚度特性和隔振性能，SLS在机械工程、结构工程和宇航工程中广泛存在，具有较高刚度和阻尼非线性，以及很高的承载能力和较优的平衡稳定性；采用摄动法和平均法研究了SLS的不同构型特点，在没有改变整体结构和外部尺寸下，SLS能显著地调节非线性刚度等非线性特征，可以满足宇航工程对隔振结构的严格要求.Friswell等[55]通过调节轴向静载以几何非线性形式改变梁的力位移特征曲线，实现高静态低动态刚度隔振，提出了两种调节方式：一是通过端部作动器改变轴向位移和转角，二是改变复合梁的初始热应力.Trung等[56]研究了QZS隔振器的Lyapunov函数主动控制方法，控制力加载在水平方向以抵消竖直方向的振动，基于Lyapunov函数发展了QZS隔振主动控制的非线性算法；实验结果表明,非直接激励的水平作动器可以通过非线性作用有效抑制竖直方向振动.Le和Ahn[57]使用负刚度主动控制系统成功实现低于5Hz的主动控制，设计模糊滑模控制(FSMC)提高了负刚度主动系统的隔振性能；基于Lyapunov稳定性理论建立模糊控制准则，通过设计实验研究了FSMC控制在不同激励环境下对系统的有效性.Danh和Ahn[58]针对车辆座椅的低频振动问题，设计了基于准零刚度的主动控制系统，利用自适应控制算法解决了该系统的时变和非线性问题，实现了高效隔振.多向准零刚度隔振器拓展了准零刚度隔振器的研究[59].徐鉴等[60]研究了多方向准零刚度隔振系统，并加入时滞主动控制,有效地抑制了多方向振动[6162].Zhou等[63]设计了6自由度刚体QZS隔振平台，运用谐波平衡法得到幅频关系；与线性6自由度隔振平台相比，能有更高效的低频隔振特性.双稳板材质轻，可操作性强，近些年倍受到隔振实验研究者们的青睐和关注.Shaw等[6465]用双稳复合板制作了质轻而有效的高静态低动态刚度的隔振系统，用实验的方法证明此系统比等价的线性系统具有更大的隔振区域以及更低的固有频率.

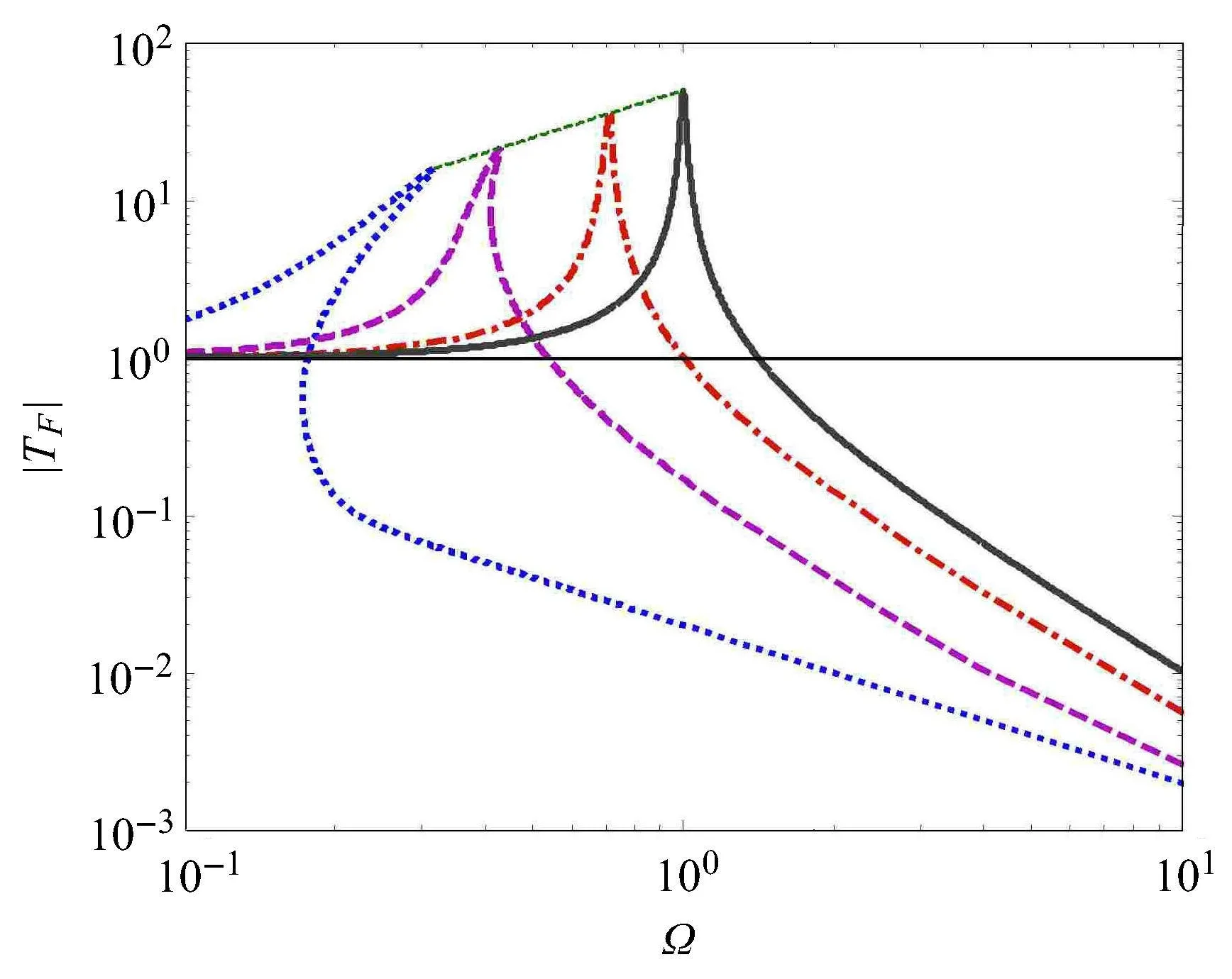
图4 不同非线性刚度下力传递率幅值|TF|[47]Fig.4 E ff ect on the force transmissibility when the nonlinear sti ff ness is changed[47]

3.2 随机分析

针对实际环境中随机非平稳的激励源，有学者提出了在随机白噪声激励下的非线性隔振系统模型[7].弹簧位移的概率密度方程可以通过福克--普朗克--柯尔莫哥洛夫(Fokker-Planck-Kolmogorov，FPK)方程的解析解获得，位移或加速度响应的均方根值被用来评价3类不同的非线性刚度：(a)立方渐硬弹簧；(b)立方渐软弹簧；(c)正切弹簧.立方渐软弹簧能有效减少振动传递率.Le和Ahn[66]用数值方法研究了车辆座椅在随机激励下时域响应，额外加入与正刚度弹簧平行的负刚度结构，建立了在低频激励下非线性隔振模型，并比较了单频、多频以及随机3种情况下隔振性能.结果表明，隔振频带均比未加入负刚度时宽，并用实验的方法验证了这一结果.橡胶隔振在工程结构中受到广泛使用，针对不同激励环境呈现出非线性和不确定因素.采用单自由度质量--弹簧--阻尼模型来简化橡胶隔振系统，其中刚度和阻尼是关于相对位移的多项式，多项式系数通过实验数据识别；主分量分析和蒙特卡洛仿真研究了系数不确定度，仿真和理论结果都表明,多项式非线性刚度非线性阻尼模型和不确定评价可以有效地预报振动特性和隔振系统不确定度[67].然而，很难获得非线性系统在随机激励下动力学分析的频域解析解，尤其是阻尼、刚度同为非线性的情况.因此，关于高静态低动态隔振系统的随机动力学行为的研究较少.

3.3 抗冲击性能

在水下潜器和航天器的振动抑制中，隔振器的抗冲击性能和隔振作用同等重要[68].冲击具有激励幅值高和瞬时特点，若不隔离会导致较大传递力和位移.传统冲击隔离是通过刚度元件变形吸收能量和阻尼耗散残余振动实现.Ledezma-Ramirez等[69]利用非线性刚度特别是低动态刚度实现冲击隔离，非线性刚度能减小绝对位移和加速度响应.非线性抗冲也可通过Euler屈曲梁实现，调节屈曲梁的曲率可以使隔振器处于QZS,Duffing型和Helmholtz-Duffing型3种工作模式，在较小激励下，与其他两类隔振模式相比，QZS并不是隔离冲击的最优形式，Duffing型含有微小正刚度能提高冲击隔离能力，Helmholtz-Duffing型隔离冲击会随着外载增加而恶化[70].

4 非线性阻尼隔振

4.1 刚度线性

Peng等[7172]和Guo等[73]使用输出频响函数较为系统地研究了立方非线性阻尼隔振器的力传递率，增加立方非线性阻尼能够减小共振频率处的力传递率并且在其他频区不受影响.Laalej等[74]实验研究了隔振系统中非线性阻尼的作用.Peng，Guo和Laalej的研究结果与Lang等[75]在早些年的研究结论相一致.Tang和Brennan[76]比较了水平阻尼(与传递振动方向垂直放置的线性阻尼[77])和立方非线性阻尼两类不同非线性阻尼的单层隔振系统的传递率特征，对于力传递率，两类阻尼都比线性阻尼具有更好的隔振特性；但对于位移传递率，水平阻尼相比立方非线性阻尼具有更多优良的特性.Xiao等[78]对比了有与没有线性项的立方非线性阻尼对单层隔振的影响，没有阻尼线性项的单纯立方非线性阻尼有更好的隔振特性，它能让力和位移传递率的共振峰压低成类似过阻尼的线性隔振系统.Lang等[79]将非线性黏性阻尼加入多自由度隔振系统，它可以描述为楼层型剪切模型，基于输出频响函数法,首次将线性黏性阻尼多自由度隔振推广到非线性情况，得到了与先前研究单自由度一致的结论.Peng等[80-81]运用输出频响函数的概念研究了多自由度隔振系统中不对称非线性阻尼作用，也得出了类似的结论.L¨u等[82]在非线性阻尼隔振的基础上，研究了周期解的稳定性.Huang等[83]研究了同时依赖速度和位移的非线性阻尼(VDD)，分别用位移和力传递率评价了VDD隔振系统性能，单自由度基础激励实验验证了理论结果.Lu等[84]实验研究了非线性阻尼的推广的麦克斯韦模型(generalized maxwell model,GMM)，阻尼非线性是通过流体阻尼的长冲程实现，GMM模型是弹簧和阻尼串联的模型.实验结果表明,GMM模型在仿真流体阻尼时在很宽的频带上都非常精确，然而麦克斯韦模型和黏滞阻尼模型只在特定频率下比较精确；进行了振动台测试实验，流体阻尼作为隔振系统的补充阻尼，GMM能够更准确地预测阻尼的能量耗散和峰值偏移.Mokni等[85]引入时滞非线性阻尼以加强隔振性能，时滞非线性阻尼通过快速参变阻尼以减小传递率，非线性阻尼能提高隔振性能.为了对非线性隔振状态监测，需要实验识别.Mu等[86]综述和比较了几种非线性阻尼隔振系统的结构故障诊断.

4.2 刚度非线性

Kovacic和Brennan[8]综述了具有非线性阻尼的3类达芬系统(渐硬、渐软和双稳)动力学特性；指出了幂函数非线性阻尼对分岔结构和通向混沌途径的影响依赖于非线性刚度特征；非线性阻尼对渐软Duffing系统的谐波响应和分岔结构，随着激励幅值的增加，两条分离的幅频曲线聚合并只存在上跳频率；上跳频率对阻尼的非线性阶次不敏感，而在较高阶次下，下跳频率随阻尼系数发生剧烈地改变，因此可以通过增加阻尼阶次来消除小阻尼带来的不稳定谐波响应；对称与不对称系统在非线性阻尼情况下，系统共振所属的分岔结构不受阻尼阶次影响，但是发生不同类型分岔的临界参数依赖于阻尼系数和阶次；渐硬Duffing振子在库伦阻尼作用下存在一些有趣的响应特征.Awrejcewicz等[87]运用谐波平衡法研究了逃脱频率(break-loose frequency)，发现激励频率大于逃脱频率时会持续较长一段时间的黏滑运动(stick-slip motion)[88].Cveticanin[89]用谐波平衡法和数值方法分别研究了正负阻尼系数与非线性阶次对振动频率的相互影响，以及极限环运动的参数边界对非线性阶次的依赖关系，数值与理论相吻合.Sharma等[90]研究了非线性阻尼对强迫达芬系统分岔与混沌特性的影响，研究结果表明,非线性阻尼能使系统首次进入混沌状态的阈值减小，并且能够增加发生混沌的参数空间，影响系统进入混沌的途径.Ho等[91]用输出频响函数法研究了非线性刚度和非线性阻尼对Duffing系统在不同频率范围内的影响.非线性黏性阻尼能够抑制共振频率处的响应,同时对高频处的响应影响较小.尽管非线性阻尼、非线性刚度系统在理论和数值上都得到了大量的研究，并且发现了一些特殊的动力学现象，但不涉及到隔振应用.

针对同时应用非线性阻尼和非线性刚度在谐波激励下的隔振问题，Ho等[92]研制了单自由度非线性阻尼、非线性刚度隔振系统，比较了线性和非线性阻尼对传递力曲线的不同影响，如图5所示.随着线性阻尼的增加，传递率峰值减小，但是高频传递率增加；随着非线性阻尼的增加，传递率峰值和跳跃频率减小，同时保持较优的高频特性[93].

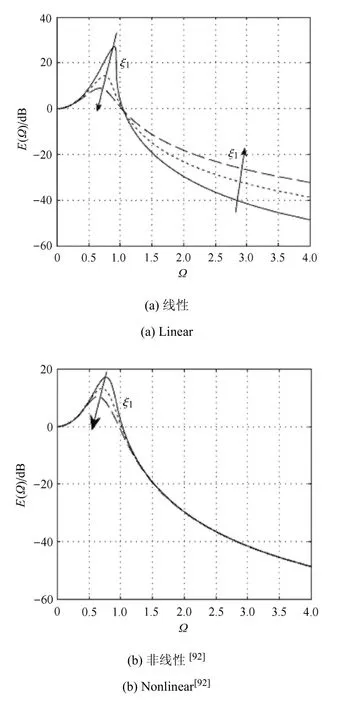
图5 比较线性和非线性阻尼对传递率的影响Fig.5 Comparison of e ff ect on transmissibility between linear and nonlinear damping

5 双层非线性隔振

双层隔振系统由于具有一些较突出的特性得到了广泛的应用[1-3,94].与单层隔振系统相比，双层隔振系统有额外的质量与刚度，因此也就有了额外的共振频率(图6).对于单层隔振系统，传递的振动在大于隔振开始频率时以40dB/oct下降，而对于双层隔振系统，它的下降率却达到80dB/oct.非线性刚度隔振系统有相对较好的低频隔振效率、较小的静态变形、不失稳性的特点，非线性阻尼能有效减小共振频率附近响应，同时对隔振区的传递率没有影响的优点.在双层线性隔振系统的上、下两层引入非线性刚度和非线性阻尼对隔振效率的影响的研究具有重要的工程与学术价值.

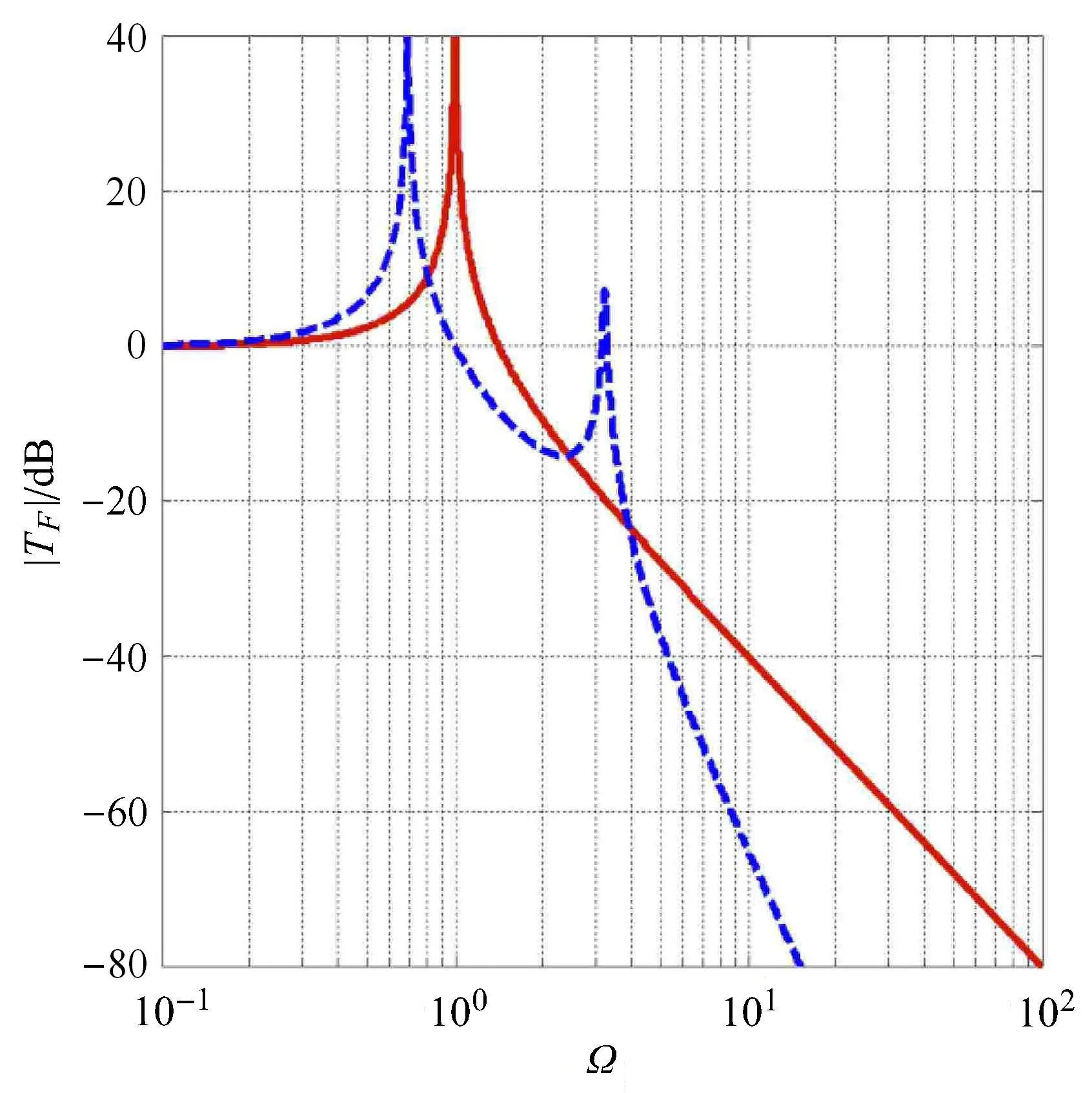
图6 单层与双层隔振系统力传递率比较(单层：红色实线，双层：蓝色虚线)[95]Fig.6 Comparison of the transmissibility of a single-stage and a two-stage linear isolator(single-stage：red solid line,two-stage：blue dashed line)[95]

Lu等[95]将高静态刚度引入到双层隔振系统中，以克服大的静态变形以及在高频处传递率曲线下降速率较缓的问题.这些几何非线性刚度是通过加入与承载刚度垂直的附加弹簧获得的，这些弹簧起负刚度的作用，因此对隔振的有效频带产生影响.这里只考虑水平弹簧能使隔振系统表现为渐硬特征的情况[95].用谐波平衡法得到单纯高静态低动态刚度双层隔振系统的力与位移传递率解析表达式，该系统的隔振效率优于双层线性隔振系统.隔振系统运动方程的矩阵形式为

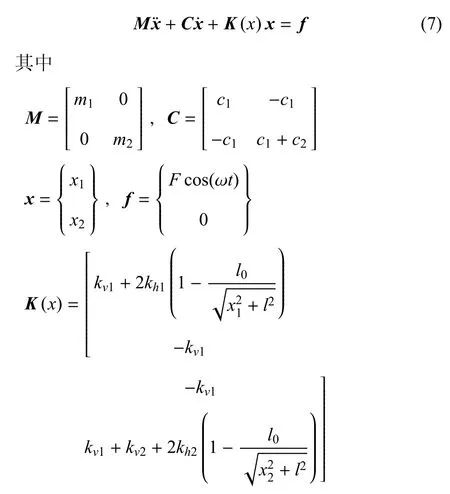
微振动情况下可以近似为两个耦合的达芬(Duffing)方程，无量纲矩阵形式如下

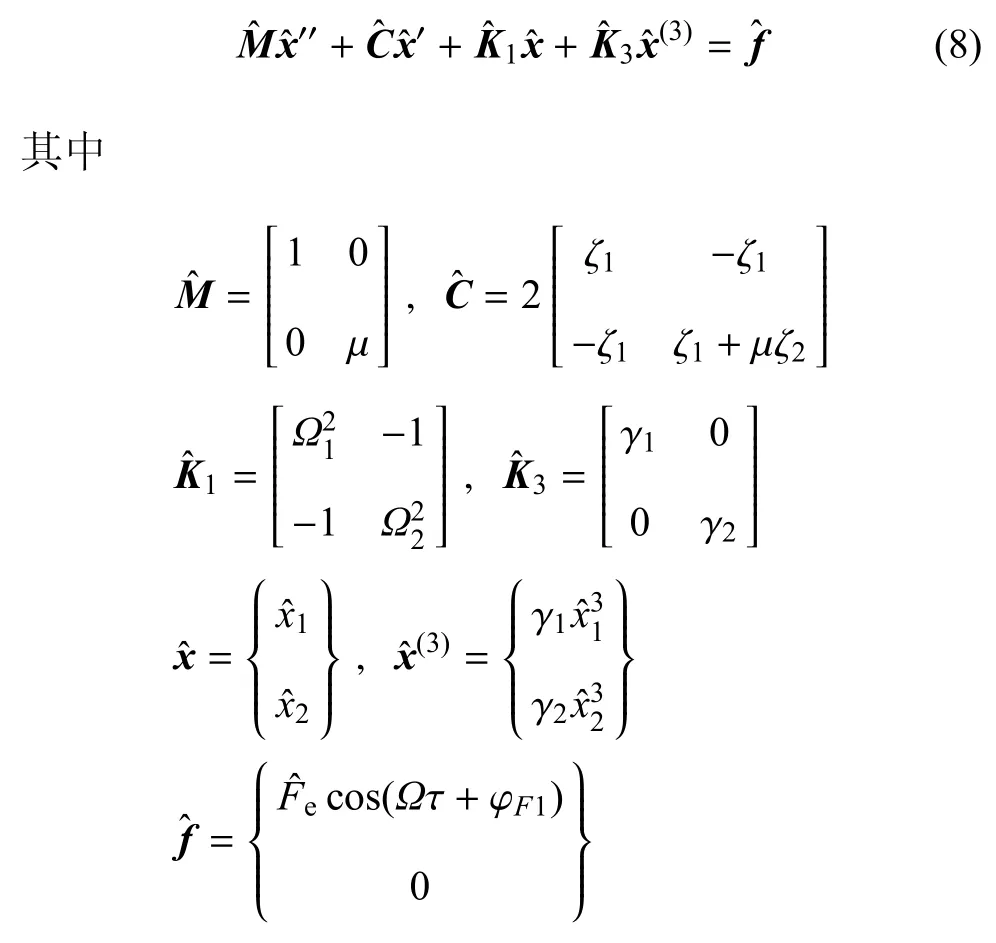
运用谐波平衡法，假设无量纲位移的向量具有如下形式

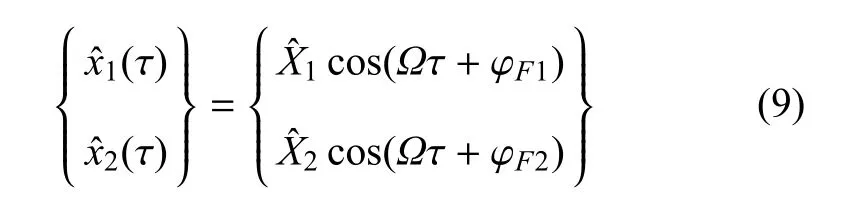
幅频矩阵方程可以表示为

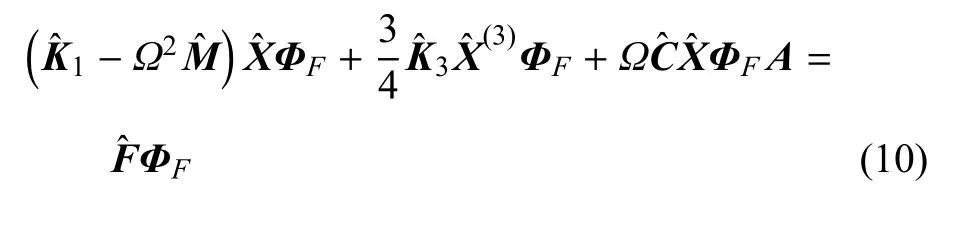
其中

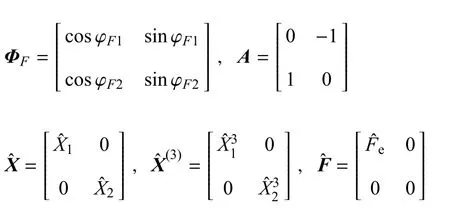
Yang等[96]研究了双层隔振系统的稳态性能，它由双稳层和线性层组成，以隔振为出发点，增加双稳层的阻尼可以改善单周期和阱内行为，但是未得到有关隔振加强的非线性正效应.Lu等[9798]在将上层非线性刚度连接到中间质量而非基础上，建立了改进的双层非线性隔振系统模型，如图7所示.与原双层非线性隔振系统相比，原系统只有改变下层的非线性刚度对改善隔振效率有效，而变化改进系统上、下层的非线性刚度对改善隔振效率均有效.双层非线性隔振兼具较低的隔振开始频率和较高隔振区传递率下降速率，受到了许多隔振研究者的关注[99].Lu等[100]还构建了紧凑的双稳复合板型负刚度单元，并将它引入到双层隔振系统，通过实验方法研究了双层高静态低动态隔振系统的隔振性能.每一层含有高静态低动态刚度；每一层中正刚度是由金属板提供，相应负刚度是由C-F双稳复合板提供.除去隔振系统中双稳复合板退化成线性双层线性隔振系统，与线性系统相比，双层非线性隔振系统在100Hz处下降13dB.

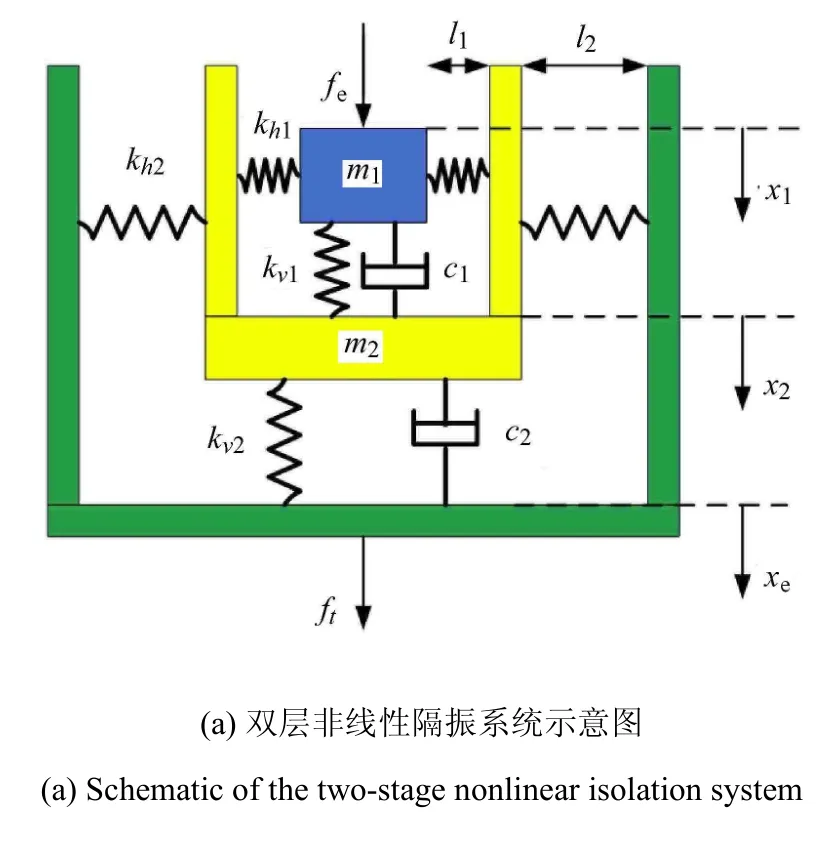
图7 改进的双层非线性隔振系统模型Fig.7 Improved two-stage nonlinear isolation system

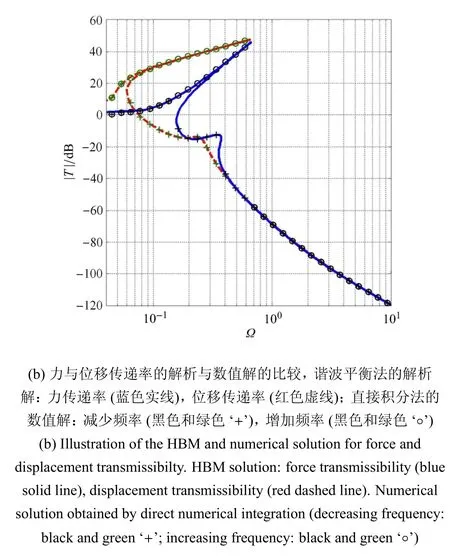
图7 改进的双层非线性隔振系统模型(续)Fig.7 Improved two-stage nonlinear isolation system(continued)

6 混沌、内共振和非线性能量阱应用于隔振

6.1 混沌隔振

混沌是非线性系统特有的动力学行为[101].当隔振系统的参数处于混沌范围时，会处于混沌状态下工作.在单频激励下，非线性系统在较宽频带内呈现混沌动力学行为.Lou和Zhu[102]利用混沌进行隔振器设计，讨论了如何减小水下潜器的辐射噪声线谱；为确保系统处于混沌态工作，确定了设计参数可取范围；传统方法是运用非线性理论分析系统和预测混沌参数的范围；但由于非线性系统的复杂性，预测参数和实际参数存在显著差别；因此有必要设置隔振系统参数可调.Liu等[103]为了确保系统在混沌状态下有效工作，提出混沌反控制方法；提出非线性隔振系统反馈模型，分析了倍周期分叉特性，通过仿真得出不同参数下多种动力学行为，最后结合混沌识别技术实验研究了自制台架(图8)在混沌状态下的隔振性能[103].

Lou和Zhu[104]还评估了非线性隔振器在混沌状态下的隔振性能，发现线谱幅值明显减少.非线性阻尼可以作为被动装置来抑制振动，Harvey等[105]提出了滚动摆隔振系统的非线性模型，研究了特定参数的滚动摆隔振系统在谐波激励下的混沌行为，并对激励幅值与激励频率的影响展开了研究.他们发现,在大幅值低频率激励下会出现混沌行为，冲击会导致周期放大和反对称分叉.最后从工程的角度提出避免隔振系统出现混沌的方法，一方面增加隔振系统可发生的位移容量，另一方面通过增加阻尼来减小实际振动位移.Farshi等[106]发展了混沌隔振系统，使用一些线性弹簧逐次进入作用的方法提供系统分段非线性，通过判断Lyapunov指数以描述系统混沌行为；通过算法比较，连续Simplex算法为结构修改的最优算法.

图8 混沌反控制隔振实验台[103]Fig.8 Nonlinear vibration isolation experimental rig for chaos anti-control technology[103]

6.2 内共振隔振

内共振是典型的非线性振动现象[107]. 涉及内共振的非线性动力系统的隔振问题得到了广泛研究[7]，这些文献都考察了达芬型刚度基础和装置刚性假设的非线性隔振系统动力学响应，刚度非线性能够在系统模态间引起耦合.1：1内共振混合模态的周期性响应会出现与线性和非线性模态共存的现象.Chen等[108]使用了增量谐波平衡法研究了非线性隔振系统的传递率和参数影响.三自由度隔振系统刚体瞬态非线性振动存在2：1：1的内共振[109]，该内共振是由于刚体的竖直振动、水平振动和绕质心转动三个自由度耦合产生.当不平衡转子的转速达到一定值时，通过共振的刚体振动非常明显.

6.3 非线性能量阱隔振

非线性能量阱(NES)是种有发展前景的减振技术[110111].当NES应用于基础激励系统的减振时，客观上起到了隔振的作用.Yang等分别对单自由度[112]和多自由度系统[113]提出了一种基于非线性输出频响函数的振动传递率表达式，首次在频域内使用该传递率概念评价NES的减振效果.研究系统为一个安装有NES的两自由度系统，对该系统进行了数值仿真分析.另外，还考察了NES的参数对该非线性系统振动传递率的影响.通过增大NES的质量和黏性阻尼，同时减小其非线性刚度，可以在所有的共振频率处减小该系统的振动传递率.因此，给出了一种在频域内设计NES非线性减振器的隔振思路.Yang等[114]针对带适配器的整星系统，设计了NES减振器；对实验缩比模型系统进行了有限元建模，并根据有限元模型得到了等效低维模型.实验结果、有限元仿真、基于等效模型的能量分析和非线性输出响应函数分析均表明，NES减振器能够有效减少基础激励向星体传递.

7 非线性隔振功能材料

非线性隔振功能材料是非线性隔振的载体[115116]，目前在隔振领域较为关注的功能材料有形状记忆合金[117121]、双稳复合板[122]、电流和磁流变液[123127]和压电晶体等.形状记忆合金等智能材料由于它的超弹性和形状记忆作用特征弥补了传统材料在隔振中的缺陷，目前使用形状记忆合金代替橡胶用于高速桥梁隔振已取得显著效果.通过非线性随机振动分析，形状记忆合金隔振能最小化隔振器位移的同时最大化隔振效率.参数研究表明，这类隔振系统还具有较强的鲁棒性[120].Xia等[119]实验研究了相位可变NiTi形状记忆合金弦线非线性扭转振动的动力学响应，通过同步获取外激励下扭角和温度以测量NiTi弦线作为非线性阻尼弹簧的热机响应，固定激励幅值测量频率响应曲线(FRCs)，固定激励频率测量幅值响应曲线(ARCs)，随着NiTi弦线变形进入渐软非线性相位转迁区域，在FRCs或ARCs分支上的稳定响应会逐渐变得不稳定并进入到新的其他任意分支；利用实验识别了FRCs和ARCs任意稳定状态间的跳跃现象和上下跳跃迟滞.通过实验识别稳定区域使得避免NiTi弦线作为非线性阻尼弹簧振动系统出现不期望的动力学响应.Ozbulut提出了形状记忆合金弹簧隔振[128]，使用形状记忆合金弹性元件实现多自由度剪切振动隔振.Choi等[129]使用形状记忆合金提出了高速桥梁的隔振轴承，通过1：1尺度模型实验研究了形状记忆合金隔振的有效性.Ozbulut等[130]综述了基于形状记忆合金的隔振系统，以及形状记忆合金在被动隔振中的应用.束立红等[131]研究了聚氨酯隔振器的弹性、弹塑性和黏弹性特点，分析了激振幅值、激振频率和预加载情况对隔振器静动态特性的影响；通过简单形状试验的静态和动态试验结果，建立了由弹簧、阻尼器和摩擦元件等多组机械元件所构成的聚氨酯隔振器“非线性广义模型”.具有高静态低动态刚度(HSLDS)的隔振系统是通过减少固有频率来提高隔振性能的，并保持一定的承载能力.高静态低动态刚度是通过在水平方向上连接线性弹簧构成突变结构(snap-through)这一常用的方法获得的，突变结构一方面增加系统的非线性，另一方面可以在一定运动区域内提供负刚度，同时线性弹簧使负刚度区域稳定化并支撑静载.由于有两个稳定的平衡形态，并且两个形态之间可以来回突变，并在突变附近板中心受力与发生横向位移存在反比关系，因此双稳复合板也可以作为负刚度装置.文献[132-137]研究了双稳板的突变响应，将这一效应用于驱动结构，研制了相应的驱动装置，这一装置能够实现多个结构状态之间转化，在转化过程中没有能量消耗，之后双稳板被广泛应用到气动变形装置上.Pirrera等[138]对双稳复合板的力位移关系曲线进行了研究，得到了负刚度曲线.使用弹性复合板壳来代替复杂的弹簧机构，具有重量轻、可操作性强的优点[139141].Shaw等[142]采用双稳板构建了负刚度结构，通过实验的方法得到了双稳板的准零力位移关系曲线.Lu等[100]构建了紧凑的双稳复合板型负刚度单元，并将它引入到双层隔振系统.

8 结论

接受结构与振源之间插入隔振元件以减小振动传递是目前最普遍的振动控制方式；高静态低动态刚度隔振系统能够克服线性隔振低频缺陷，是振动控制领域研究的主要热点之一；非线性阻尼能够抑制线性系统共振频率处响应，同时保持较优高频隔振性能.本文综述了非线性隔振的新进展，主要包括非线性隔振评价方式、高静态低动态刚度隔振及其加强形式非线性阻尼加强和双层非线性隔振、混沌、内共振和非线性能量阱在隔振中的应用和非线性隔振功能材料.

非线性隔振应用背景广泛如整星隔振、船舶海洋工程结构物隔振等，根据不同应用背景特点，非线性隔振器大小不同、形状各异.非线性隔振由于出现倍周期、准周期和混沌等丰富的非线性动力学行为，通常需要响应与激励的均方根值之比代替幅值比以评价非线性隔振效果，对于柔性基础，还需要从功率流角度来评估.动力学响应的研究中，既有确定性分析又有随机分析；在研究方法的应用中，有谐波平衡法等解析方法、有限元法等数值方法和实验方法.非线性隔振的实现结构有几何非线性和材料非线性，几何非线性结构通常是金属弹簧、梁、板和壳等通过几何构造实现非线性隔振功能、材料非线性结构通常是利用双稳复合板、形状记忆合金、电流/磁流变液等新材料实现特殊非线性刚度和非线性阻尼功能，提高隔振性能.

本文针对非线性隔振理论与应用开展了全面综述和深入分析，在此基础上，今后还可以在以下几方面继续开展研究：

(1)非线性隔振系统的主共振、亚谐共振和超谐共振稳定性及分岔，从稳定性裕度、吸引域角度提高非线性隔振系统的设计水平；

(2)非线性刚度非线性阻尼隔振系统抗冲击特性，冲击激励具有作用时间短、阻尼作用不明显等特点；

(3)在结构和隔振器发生内共振情况下随机振动传递特性，非线性模态间作用对隔振性能的影响，明确在随机坏境下内共振的动力学机制；

(4)金属弹簧、梁、板和壳的各种不同屈曲构型特点以实现非线性隔振，碳纤维--压电晶体复合板材等新材料的特殊非线性刚度、非线性阻尼特性以克服传统金属材料隔振缺陷；

(5)非线性隔振与能量采集一体化，适应集成化、轻质小体化发展，结构兼具隔振和能量采集等多种用途.

1 Mead DJ,Meador D.Passive Vibration Control.Chichester：Wiley,1998

2 Harris CM,Piersol AG.Harris’Shock and Vibration Handbook.New York：McGraw-Hill,2002

3 Rivin EI.Passive Vibration Isolation,New York：ASME press,2003

4 Fuller CC,Elliott S,Nelson PA.Active Control of Vibration.New York：Academic Press,1996

5 Hansen C,Snyder S.Active Control of Noise and Vibration.London：E&FN Spon,1997

6 Gawronski WK.Advanced Structural Dyanmaics and Active Control of Structures.New York：Springer,2004

7 Ibrahim R.Recent advances in nonlinear passive vibration isolators.Journal of Sound and Vibration,2008.314(3)：371-452

8 Kovacic I,Brennan MJ.The Duffing Equation：Nonlinear Oscillators and Their Behaviour.UK：John Wiley&Sons,2011

9董瑶海.航天器微振动：理论与实践.北京：中国宇航出版社,2015(Dong Yaohai.Micro-Vibration of Aircraft：Theoretic and Practice.Beijing：China Astronautic Publishing House,2015(in Chinese))

10 Kandasamy R,Cui F,Townsend N,et al.A review of vibration control methods for marine o ff shore structures.Ocean Engineering,2016,127：279-297

11马兴瑞.动力学振动与控制新进展(航天技术专著).北京：中国宇航出版社,2010(Ma Xingrui.Recent Advances in Dynamics Vibration and Control.Beijing：China Astronautic Publishing House,2010(in Chinese))

12黄文虎,曹登庆,韩增尧.航天器动力学与控制的研究进展与展望.力学进展,2012,42(4)：367-393(HuangWenhu,CaoDengqing,Han Zengyao.Advances and trends in dynamics and control of spacecrafts.Advances in Mechanics,2012,42(4)：367-393(in Chinese))

13 Zheng G,Tu Y.Analytical study of vibration isolation between a pair of fl xible structures.ASME Journal of Vibration and Acoustics,2009,31(6)：1-10

14 Zhang Y,Zhang J.Disturbances characteristics analysis of a control moment gyroscope due to imbalances and installation errors.IEEE Transactions on Aerospace and Electronic Systems,2014,50(2)：1017-1026

15 Zhang Y,Zhang J,Xu S.Parameters design of vibration isolation platform for control moment gyroscopes.Acta Astronautica,2012,81(2)：645-659

16 Zhang Y,Zhang J,Xu S.Influenc of fl xible solar arrays on vibration isolation platform of control moment gyroscopes.Acta Mechanica Sinica,2012,28(5)：1479-1487

17 ZhangY,ZhangJ,ZhaiG.Vibrationisolationplatformwithmultiple tuned mass dampers for reaction wheel on satellites.Mathematical Problems in Engineering,2013,4：1-14

18 Zhang Y,Zhang J.The imaging stability enhancement of optical payload using multiple vibration isolation platforms.Journal of Vibration and Control,2013,21(9)：1848-1865

19 Zhang Y,Guo Z,He H,et al.A novel vibration isolation system for reaction wheel on space telescopes.Acta Astronautica,2014,102：1-13

20 Haritos N.Introduction to the analysis and design of o ff shore structures-an overview.Electronic Journal Structural Engineering,2007,7：55-65

21 Bajkowski JM,Dyniewicz B,Bajer CI.Semi-active damping strategy for beams system with pneumatically controlled granular structure.Mechanical System and Signal Process,2016,70：387-396

22 Chakrabarti S.Handbook of O ff shore Engineering.Oxford：Elsevier,2015

23 Bargi K,Hosseini SR,Tadayon MH,et al.Seismic response of a typical fi ed jacket-type o ff shore platform(spd1)under sea waves.Open Journal of Marine Science,2011,1(02)：36

24 Chandrasekaran S,Kumar D,Ramanathan R.Dynamic response of tension leg platform with tuned mass dampers.Journal of Naval Architecture and Marine Engineering,2013,10(2)：149-156

25 Caterino N.Semi-active control of a wind turbine via magnetorheological damper.Journal of Sound and Vibration,2015,345：1-17

26 Lu Z,Brennan MJ,Chen L.On the transmissibilities of nonlinear vibration isolation system.Journal of Sound and Vibration,2016,375：28-37

27 Xie S,Or SW,Chan HLW,et al.Analysis of vibration power fl w from a vibration machinery to a floatin elastic panel.Michanical Systems and Signal Processing,2007,21：389-404

28 Choi WJ,Xiong YP,Shenoi RA.Power fl w analysis for a floatin sandwich raft isolation system using a higher-order theory.Journal of Sound and Vibration,2009,319：228-246

29 Xing JT.EnergyFlow Theory of Nonlinear Dynamical Systems with Applications.Switzerland：Springer,2015

30马业忠,霍睿.板式基础上非线性隔振系统的功率流传递特性.振动工程学报,2008,21(4)：394-397(Ma Yezhong,Huo Rui.Characteristic of power fl w transmission in nonlinear vibration isolation systemonplatebase.JournalofVibrationEngineering,2008,21(4)：394-397(in Chinese))

31高书磊,霍睿.柔性基础上非线性隔振系统的动力学分析.振动与冲击,2007,26(6)：113-116(Gao Shulei,Huo Rui.E ff ect of nonlinear parameter of isolator on equipment’s kinetic energy.Journal of Vibration and Shock,2007,26(6)：113-116(in Chinese))

32 Royston TJ,Singh R.Vibratory power fl w through a nonlinear path into a resonant receiver.Journal of the Acoustical Society of America,1997,101：2059-2069

33 Xiong YP,Xing JT,Price WG.Interactive power fl w characteristics of an integrated equipment-nonlinear isolator-travelling fl xible ship excited by sea waves.Journal of Sound and Vibration,2005,287：245-276

34 Kerschen G,Peeters M,Golinval JC,et al.Nonlinear normal modes,Part I：a useful frame work for the structural dynamicist.Mechanical System and Signal Processing,2009,23：170-194

35 Yang J,Xiong YP,Xing JT.Dynamics and power fl w behavior of a nonlinear vibration isolation system with a negative sti ff ness mechanism.Journal of Sound and Vibration,2013,332：167-183

36 Yang J,Xiong YP,Xing JT.Nonlinear power fl w analysis of the Duffing oscillator. Mechanical Systems and Signal Processing,2014,45：563-578

37 Yang J,Xiong YP,Xing JT.Vibration power fl w and force transmission behavior of a nonlinear isolator mounted on a nonlinear base.International Journal of Mechanical Sciences,2016,115-116：238-252

38 Ahn HJ.Performance limit of a passive vertical isolator using a negative sti ff ness mechanism.Journal of Mechanical Scinence and Technology,2008,22：2357-2367

39 Kim KR,You YH,Ahn HJ.Optimal design of a QZS isolator using fl xures for a wide range of payload.International Journal of Precision Engineering and Manufacturing,2013,14(6)：911-917

40 RobertsonWS,KidnerMRF,CazzolatoBS,etal.Theoreticaldesign parameters for a quasi-zero sti ff ness magnetic spring for vibration isolation.Journal of Sound and Vibration,2009,326(1)：88-103

41 Shin K.On the performance of a single degree-of-freedom highstatic-low-dynamic sti ff ness magnetic vibration isolator.International Journal of Precision Engineering and Manufacturing,2014,15(3)：439-445

42彭超,龚兴龙,宗路航等.新型非线性低频被动隔振系统设计及实验研究.振动与冲击,2013,32(3)：6-11(Peng Chao,Gong Xinglong,Zong Luhang,et al.Design and tests for a new type nonlinear low-frequency passive vibration isolation system.Journal of Vibration and Shock,2013,32(3)：6-11(in Chinese))

43路纯红,白鸿柏.新型超低频非线性被动隔振系统的设计.振动与冲击,2011,30(1)：234-236(Lu Chunhong,Bai Hongbai.A new type nonlinear ultra-low frequency passive vibration isolation system.Journal of Vibration and Shock,2011,30(1)：234-236(in Chinese))

44 Carrella A,Brennan MJ,Waters TP.Static analysis of a passive vibration isolator with quasi-zero-sti ff ness characteristic.Journal of Sound and Vibration,2007,301(3)：678-689

45 Kovacic I,Brennan MJ,Waters TP.A study of a nonlinear vibration isolator with a quasi-zero sti ff ness characteristic.Journal of Sound and Vibration,2008,315：700-711

46 Carrella A,Brennan MJ,Kovacic I,et al.On the force transmissibility of a vibration isolator with quasi-zero-sti ff ness.Journal of Sound and Vibration,2009,322(4)：707-717

47 Carrella A,Brennan MJ,Waters TP,et al.Force and displacement transmissibility of a nonlinear isolator with high-static-lowdynamic-sti ff ness.International Journal of Mechanical Sciences,2012,55(1)：22-29

48 Xu D,Yu Q,Zhou J,et al.Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-sti ff ness characteristic.Journal of Sound and Vibration,2013,332：3377-3389

49 Sun X,Xu J,Jing X,et al.Beneficia performance of a quasi-zerosti ff ness vibration isolator with time-delayed active control.International Journal of Mechanical Science,2014,82：32-40

50 Li Q,Zhu Y,Xu D,et al.A negative sti ff ness vibration isolator using magnetic spring combined with rubber membrane.Journal of Mechanical Scinece and Technology,2013,27(3)：813-824

51 Huang X,Liu X,Hua H.On the characteristics of an ultra-low frequency nonlinear isolator using sliding beam as negative sti ff ness.Journal of Mechanical Science and Technology,2014,28(3)：813-822

52 Huang X,Liu X,Sun J,et al.E ff ect of the system imperfections on the dynamic response of a high-static-low-dynamic sti ff ness vibration isolator.Nonlinear Dynamics,2014,76：1157-1167

53 Sun XT,Jing XJ,Xu J,et al.Vibration isolation via a scissor-like structured platform.Journal of Sound and Vibration,2014,333(9)：2404-2420

54 ZhangW,ZhaoJ.Analysisonnonlinearsti ff nessandvibrationisolation performance of scissor-like structure with full types.Nonlinear Dynamics,2016,86：17-36

55 Friswell MI,Saavedra Flores EI.Dynamic isolation systems using tunable nonlinear sti ff ness beams.The European Physical Journal Special Topics,2013,222：1563-1573

56 Trung PV,Kim KR.,Ahn HJ.A nonlinear control of an QZS isolator with fl xures based on a Lyapunov function.International Journal of Precision Engineering and Manufacturing,2013,14(6)：919-924

57 Le TD,Ahn KK.Fuzy sliding mode controller of a pneumatic active isolation system using negative sti ff ness structure.Journal of Mechanical Science and Technology,2012,26(12)：3873-3884

58 Danh LT,Ahn KK.Active pneumatic vibration isolation system using negative sti ff ness structures for a vehicle seat.Journal of Sound and Vibration,2014,333(5)：1245-1268

59徐鉴.振动控制研究进展综述.力学季刊,2015,36(4)：547-565(Xu Jian.Advances of research on vibration control.Chinese Quarterly of Mechanics,2015,36(4)：547-565(in Chinese))

60 Xu J,Sun XT.A multi-directional vibration isolator based on quasizero-sti ff ness structure and time-delayed active control.International Journal of Mechanical Sciences,2015,100：126-135

61 Sun XT,Jing XJ,Xu J,et al.A quasi-zero-sti ff ness-based sensor system in vibration measurement.IEEE Transactions on Industrial Electronics,2014,61(10)：5606-5614

62 Sun XT,Jing XJ,Cheng L,et al.A 3D quasi-zero-sti ff ness based sensor system for absolute motion measurement and application in active vibration control.IEEE/ASME Transactions on Mechatronics,2015,20(1)：254-262

63 Zhou J,Xiao Q,Xu D,et al.A novelquasi-zero-sti ff ness strut and its applications in six-degree-of-freedom vibration isolation platform.Journal of Sound and Vibration,2017,(in press)

64 Shaw A,Neild S,Wagg D,et al.A nonlinear spring mechanism incorporating a bistable composite plate for vibration isolation.Journal of Sound and Vibration,2013,332(24)：6265-6275

65 Shaw A,Neild S,Wagg D.Dynamic analysis of high static low dynamic sti ff ness vibration isolation mounts.Journal of Sound and Vibration,2013,332(6)：1437-1455

66 Le TD,Ahn KK.A vibration isolation system in low frequency excitation region using negative sti ff ness structure for vehicle seat.Journal of Sound and Vibration,2011,330(26)：6311-6335

67 Chen X,Shen Z,He Q,et al.Influenc of uncertainty and excitation amplitude on the vibration characteristics of rubber isolators.Journal of Sound and Vibration,2016,377：216-225

68 Virgin L,Davis R.Vibration isolation using buckled struts.Journal of Sound and Vibration,2003,260：965-973

69 Ledezma-Ramirez D,Ferguson N,Brennan MJ,et al.An experimental nonlinear low dynamic sti ff ness device for shock isolation.Journal of Sound and Vibration,2015,347：1-13

70 Huang X,Chen Y,Hua H,et al.Shock isolation performance of a nonlinear isolator using Euler buckled beam as negative sti ff ness corrector：Theoretical and experimental study.Journal of Sound and Vibration,2015,345：178-196

71 Peng Z,Meng G,Lang Z,et al.Study of the e ff ects on cubic nonlinear damping on vibration isolations using Harmonic Balance Method.International Journal of Non-linear Mechanics,2012,47：1073-1080

72 Peng Z,Lang Z,Zhao L,et al.The force transmissibility of MDOF structures with a non-linear viscous damping device.International Journal of Non-Linear Mechanics,2011,46：1305-1314

73 Guo P,Lang Z,Peng Z.Analysis and design of the force and displacement transmissibility of nonlinear viscous damper based vibration isolation system.Nonlinear Dynamics,2012,67：2671-2687

74 Laalej H,Lang Z,Daley S,et al.Application of non-linear damping to vibration isolation：an experimental study.Nonlinear Dynamics,2012,69：409-421

75 Lang Z,Jing X,Billings SA,et al.Theoretical study of the e ff ects of nonlinear viscous damping on vibration isolation of sdof systems.Journal of Sound and Vibration,2009,323(1)：352-365

76 Tang B,Brennan MJ.A comparison of two nonlinear damping mechanisms in a vibration isolator.Journal of Sound and Vibration,2013,332(3)：510-520

77 Sun J,Huang X,Liu X,et al.Study on the force transmissibility of vibration isolators with geometric nonlinear damping.Nonlinear Dynamics,2013,74：1103-1112

78 Xiao Z,Jing X,Cheng L.The transmissibility of vibration isolators with cubic nonlinear damping under both force and base excitations.Journal of Sound and Vibration,2013,332(5)：1335-1354

79 Lang Z,Guo P,Takewaki I.Output frequency response function based design of additional nonlinear viscous dampers for vibration control of multi-degree-of-freedom systems.Journal of Sound and Vibration,2013,332：4461-4481

80 Peng Z,Lang Z.E ff ects of anti-symmetric nonlinear viscous damping on the force transmissibility of multi-degree of freedom structures.Theoretical&Applied Mechanics Letters,2011,1：063004

81 Peng Z,Lang Z,Meng G,et al.Reducing force transmissibility in multiple degrees of freedom structures through anti-symmetric nonlinear viscous damping.Acta Mechanica Sinica,2012,28(5)：1436-1448

82 L¨u Q,Yao Z.Analysis of the e ff ects of nonlinear viscous damping on vibration isolator.Nonlinear Dynamics,2015,79：2325-2332

83 Huang X,Sun J,Hua H,et al.The isolation performance of vibration systems with general velocity-displacement-dependent nonlinear damping under base excitation：Numerical and experimental study.Nonlinear Dynamics,2016,85：77-796

84 Lu L,Lin G,Shih M.An experimental study on a generalized Maxwell model for nonlinear viscoelastic dampers used in seismic isolation.Engineering Structures,2012,34：111-123

85 Mokni L,Belhaq M.Using delayed damping to minimize transmitted vibrations.Communications in Nonlinear Science and Numerical Simulation,2012,17：1980-1985

86 Mu T,Zhou L,Yang JN.Comparison of adaptive structural damage identificatio techniques in nonlinear hysteretic vibration isolation systems.Earthquake Engineering and Engineering Vibration,2013,12(4)：659-667

87 Awrejcewicz J,Olejnik P.Stick-slip dynamics of a two-degree-offreedom system.International Journal of Bifurcation and Chaos,2003,13(4)：843-861

88 Bhattacharya B.Principles of Vibration Control.New York：Wiely,2014

89 CveticaninL.Onthetrulynonlinearoscillatorwithpositiveandnegative damping.Applied Mathematics and Computation,2014,243：433-445

90 Sharma A,Patidar V,Purohit G.E ff ects on the bifurcation and chaos in forced Duffing oscillator due to nonlinear damping.Communications in Nonlinear Science and Numerical Simulation,2012,17：2254-2269

91 Ho C,Lang Z,Billings S.A frequency domain analysis of the e ff ects of nonlinear damping on the Duffing equation.Mechanical Systems and Signal Processing,2014,45(1)：49-67

92 Ho C,Lang Z,Billings S.Design of vibration isolators by exploiting the beneficia e ff ects of sti ff ness and damping nonlinearities.Journal of Sound and Vibration,2014,333(12)：2489-2504

93 Huang D,Xu W,Xie W,et al.Dynamical properties of a forced vibration isolation system with real-power nonlinearities in restoring and damping forces.Nonlinear Dynamics,2015,81：641-658

94汪玉,陈国均,华宏星等.船舶动力装置双层隔振系统的优化设计.中国造船,2001,42(1)：45-49(Wang Yu,Chen Guojun,Hua Hongxing,et al.Optimal design of ship floatin raft system power equipment.Ship Building of China,2001,42(1)：45-49(in Chinese))

95 Lu Z,Brennan MJ,Yang T,et al.An investigation of a two-stage nonlinear vibration isolation system.Journal of Sound and Vibration,2013,332(6)：1456-1464

96 Yang K,Harne RL,Wang K,et al.Investigation of a bistable dualstage vibration isolator under harmonic excitation.Smart Materials and Structures,2014,23(4)：045033

97 Lu Z,Yang T,Brennan MJ,et al.On the performance of a twostage vibration isolation system which has geometrically nonlinear sti ff ness.ASME Journal of Vibration and Acoustics,2014,136(6)：064501

98 Wang Y,Li S,Neild SA,et al.Comparison of the dynamic performance of nonlinear one and two degree-of-freedom vibration isolators with quasi-zero sti ff ness.Nonlinear Dynamics,2017(in press)

99 Wang X,Zhou J,Xu D,et al.Force transmissibility of a two-stage vibration isolation system with quasi-zero sti ff ness.Nonlinear Dynamics,2017,87：633-646

100 Lu Z,Yang T,Brennan MJ,et al.Experimental investigation of a two-stage nonlinear vibration isolation system with high-static-lowdynamic sti ff ness.ASME Journal of Applied Mechanics,2017,84：021001-1

101 Moon FC.Chaotic and Fractal Dynamics：An introduction for applied scientists and engineers.Weinheim：Wiley-VCH,2004

102 Lou J,Zhu S,He L,et al.Application of chaos method to line spectra reduction.Journal of Sound and Vibration,2005,286：645-652

103 Liu S,Yu X,Zhu S.Study on the chaos anti-control technology in nonlinear vibration isolation system.Journal of Sound and Vibration,2008,310：855-864

104 Lou J,Zhu S,He L,et al.Experimental chaos in nonlinear vibration isolation system.Chaos Solitons&Fractals,2009,40：1367-1375

105 Harvey JrPS,Wiebe R,Gavin HP.On the chaotic response of a nonlinear rolling isolation system.Physica D:Nonlinear Phenomena,2013,256-257：36-42

106 Farshi B,Assadi A.Development of a chaotic nonlinear tuned mass damper for optimal vibration response.Communication in Nonlinear Science and Numerical Simulation,2011,16：4514-4523

107 Nayfeh,AH.Nonlinear Interactions：Analytical,Computational,and Experimental Methods.Wiley：New York,1998

108 Chen Y,Chen S.Response and transmissibility of nonlinear isolating systems.Journal of Vibration and Shock,1998,17：18-22

109 Kawana R,Tokoyoda T,Sato K,et al.Passage through resonance in a three-degree-of-freedom vibration isolation system.Transactions of the Japan Society of Mechanical Engineers,Part C,2006,72(7)：2034-2041

110 Lee YS,Vakakis AF,Bergman LA,et al.Passive non-linear targeted energy transfer and its applications to vibration absorption：a review.Journal of Multi-body Dynamics,2008,222：77-134

111 Vakakis AF,Gendelman OV,Bergman LA,et al.Nonlinear Targeted Energy Transfer in Mechanical and Structural Systems.Springer：Netherlands,2009

112 Yang K,Zhang Y,Ding H,et al.The transmissibility of nonlinear energysinkbasedonnonlinearoutputfrequency-responsefunctions.Communications in Nonlinear Science and Numerical Simulation,2017,44：184-192

113杨凯,张业伟,丁虎等.基于非线性输出频响函数的NES动力学参数设计.振动与冲击,2016,35(21)：76-80(Yang Kai,Zhang Yewei,Ding Hu,et al.Parametric design of nonlinear energy sinks based on nonlinear output frequency-response functions.Journal of Vibration and Shock,2016,35(21)：76-80(in Chinese))

114 Yang K,Zhang Y,Ding H,et al.Nonlinear energy sink for wholespacecraft vibration reduction.ASME Journal of Vibration and Acoustics,2017,139(2)：021011

115 Harris DA.Vibration Isolation Materials//Noise Control Manual.New York：Springer,1991

116 Thenozhi S,Yu W.Advances in modeling and vibration control of building structures.Annual Reviews in Control,2013,37(2)：346-364

117 Rustighi E,Brennan M,Mace B.A shape memory alloy adaptive tuned vibration absorber：Design and implementation.Smart materials and Structures,2005,14(1)：19

118 Bonello P,Brennan MJ,Elliott SJ,et al.Designs for an adaptive tuned vibration absorber with variable shape sti ff ness element.Proceedings of the Royal Society A:Mathematical,Physical and Engineering Science,2005,461(2064)：3955-3976

119 Xia M,Sun Q.Thermomechanical responses of nonlinear torsional vibration with NiTi shape memory alloy-alternative stable states and their jumps.Journal of the Mechanics and Physics of Solids,2016,(in press)

120 Damanpack A,Bodaghi M,Aghdam M,et al.On the vibration control capability of shape memory alloy composite beam.Composite Structure,2014,110：325-334

121 Shinozuka M,Chaudhuri SR,Mishra SK.Shape-Menory-Alloy supplemented lead rubber bearing(SMA-LRB)for seismic isolation.Probabilistic Engineering Mechanics,2015,41：34-45

122 Shaw AD,Carrella A.Force displacement curves of a snapping bistable Plate.Nonlinear Dynamics,2012,3：191-197

123 York D,Wang X,Gordaninejad F.A new MR fluid-elastome vibration isolator.Journal of Intelligent Material Systems and Structures,2007,18(12)：1221-1225

124 Liao W,Lai C.Harmonic analysis of a magnetorheological damper for vibration control.Smart Materials and Structures,2002,11(2)：288

125 SimsN,PeelD,StanwayR,etal.Theelectrorheologicallong-stroke damper：A new modelling technique with experimental validation.Journal of Sound and Vibration,2000,229(2)：207-227

126 Dutta S,Chakraborty G.Performance analysis of nonlinear vibration isolator with magneto-rheological damper.Journal of Sound and Vibration,2014,333：5097-5114

127 Yu H,Sun X,Xu J,et al.The time-delay coupling nonlinear e ff ect in sky-hook control of vibration isolation systems using Magneto-Rheological fluidampers.Journal of Mechanical Science and Technology,2016,30(9)：4157-4166

128 OzbulutOE,RoschePN,LinPY,etal.GA-basedoptimumdesignof a shape memory alloy device for seismic response mitigation.Smart Material and Structure,2010,19：065004

129 Choi E,Nam TH,Oh JT,et al.An isolation bearing for highway bridges using shape memory alloys.Material Science Engineering,2006,438-440：1081-1084

130 Ozbulut OE,Hurlebaus S,Desroches R.Seismic response control using shape memory alloys：A review.Journal of Intelligent Material System and Stucture,2011,22：1531-1549

131束立红,何琳,王宇飞等.聚氨酯隔振器非线性力学模型与特性研究.振动工程学报,2010,23(5)：530-536(Shu Lihong,He Lin,Wang Yufei,et al.Nonlinear mechanical model and character research on polyurethane isolator.Journal of Vibration Engineering,2010,23(5)：530-536(in Chinese))

132 Daynes S,Nall S,Weaver P,et al.Bistable composite fla for an airfoil.Journal of Aircraft,2010,47(1)：334-338

133 Daynes S,Weaver P,Trevarthen J.A morphing composite air inlet with multiple stable shapes.Journal of Intelligent Material Systems and Structures,2011,22(9)：961-973

134 Schultz MR.A concept for airfoil-like active bistable twisting structures.Journal of Intelligent Material Systems and Structures,2008,19(2)：157-169

135 Gatto A,Mattioni F,Friswell M.Experimental investigation of bistable winglets to enhance aircraft wing lift takeo ffcapability.Journal of Aircraft,2009,46(2)：647-655

136 Diaconu CG,Weaver PM,Mattioni F.Concepts for morphing airfoil sections using bi-stable laminated composite structures.Thin-Walled Structures,2008,46(6)：689-701

137 Lachenal X,Daynes S,Weaver PM.Review of morphing concepts and materials for wind turbine blade applications.Wind Energy,2013,16(2)：283-307

138 Pirrera A,Avitabile D,Weaver P.Bistable plates for morphing structures：a refine analytical approach with high-order polynomials.International Journal of Solids and Structures,2010,47(25)：3412-3425

139 Potter K,Weaver P,Seman AA,et al.Phenomena in the bifurcation of unsymmetric composite plates.Composites Part A:Applied Science and Manufacturing,2007,38(1)：100-106

140 TawfiS,Tan X,Ozbay S,et al.Anticlastic stability modeling for cross-ply composites.Journal of Composite Materials,2007,41(11)：1325-1338

141 Diaconu CG,Weaver PM,Arrieta AF.Dynamic analysis of bi-stable composite plates.Journal of Sound and Vibration,2009,322(4)：987-1004

142 Shaw AD,Neild SA,Wagg DJ,et al.A nonlinear spring mechanism incorporating a bistable composite plate for vibration isolation.Journal of Sound and Vibration,2013,332(24)：6265-6275

SOME RECENT PROGRESSES IN NONLINEAR PASSIVE ISOLATIONS OF VIBRATIONS1)

Lu Zeqi∗Chen Liqun∗,†,2)∗(Shanghai Institute of Applied Mathematics and Mechanics,Shanghai University，Shanghai 200072，China)†(Department of Mechanics，Shanghai University，Shanghai 200444，China)

Vibrations in aircraft and marine structures,due to various extreme environmental loads,have been attributing factors in accidents and failures.Over the last decade,as the demands for vibration and shock isolation performance increasing,the general approaches following the conventional categorization of passive,active,semi-active and hybrid has been extensive presented.Nonlinear passive vibration isolation is the state of the art of vibration control techniques for combining robustness of the passive device and high performance of the active devices.This paper surveys theoretical and practical advances in nonlinear passive isolation of vibration in recent ten years.Sti ff ness and damping both nonlinearities is considered in modeling of vibration isolation system;Deterministic and stochastic analysis are both conducted on the investigation of the dynamic behavior.Initially,a review of a general approach to quantify the e ff ectiveness of nonlinear vibrations isolation is presented.This is then followed by a review of high-static-low-dynamic sti ff ness vibration isolation,damping nonlinearity vibration isolation,two-stage nonlinear vibration isolation and nonlinear vibration isolation materi-als.The other vibration isolation methods considered in this review include chaotic anti-control technology,influenc of internal resonance and usage of nonlinear energy sink.The article is closed by conclusions,which highlight resolved and unresolved problems and recommendations for future research treads.

vibration isolation，nonlinear vibration，high static low dynamic sti ff ness，nonlinear damping，isolation materials

O328

：A

10.6052/0459-1879-17-064

2017–03–01 收稿，2017–04–20 录用,2017–04–21 网络版发表.

1)国家自然科学基金重点项目(11232009)和国家自然科学基金项目(11502135,11572182)资助.

2)陈立群，教授，主要研究方向：非线性动力学和振动控制.E-mail：lqchen@sta ff.shu.edu.cn

陆泽琦,陈立群.非线性被动隔振的若干进展.力学学报,2017,49(3)：550-564

Lu Zeqi,Chen Liqun.Some recent progresses in nonlinear passive isolations of vibrations.Chinese Journal of Theoretical and Applied Mechanics,2017,49(3)：550-564