基于制造解的非结构二阶有限体积离散格式的精度测试与验证1)

王年华 张来平 赵 钟 赫 新

∗(中国空气动力研究与发展中心计算空气动力研究所，四川绵阳621000)†(中国空气动力研究与发展中心空气动力学国家重点实验室，四川绵阳621000)

基于制造解的非结构二阶有限体积离散格式的精度测试与验证1)

王年华∗,2)张来平∗,†赵 钟∗赫 新∗,†

∗(中国空气动力研究与发展中心计算空气动力研究所，四川绵阳621000)†(中国空气动力研究与发展中心空气动力学国家重点实验室，四川绵阳621000)

随着计算机技术的飞速进步，计算流体力学得到迅猛发展，数值计算虽能够快速得到离散结果，但是数值结果的正确性与精度则需要通过严谨的方法来进行验证和确认.制造解方法和网格收敛性研究作为验证与确认的重要手段已经广泛应用于计算流体力学代码验证、精度分析、边界条件验证等方面.本文在实现标量制造解和分量制造解方法的基础上，通过将制造解方法精度测试结果与经典精确解(二维无黏等熵涡)精度测试结果进行对比，进一步证实了制造解精度测试方法的有效性，并将两种制造解方法应用于非结构网格二阶精度有限体积离散格式的精度测试与验证，对各种常用的梯度重构方法、对流通量格式、扩散通量格式进行了网格收敛性精度测试.结果显示,基于Green-Gauss公式的梯度重构方法在不规则网格上会出现精度降阶的情况，导致流动模拟精度严重下降，而基于最小二乘(least squares)的梯度重构方法对网格是否规则并不敏感.对流通量格式的精度测试显示,所测试的各种对流通量格式均能达到二阶精度，且各方法精度几乎相同；而扩散通量离散中界面梯度求解方法的选择对流动模拟精度有显著影响.

验证与确认，制造解方法，精确解方法，网格收敛性研究，有限体积离散方法，数值模拟精度

引言

自从20世纪中叶计算流体力学(computational fluidynamics,CFD)诞生以来，随着计算机技术和CFD方法的迅速发展，CFD数值模拟技术已经广泛应用于以航空航天为代表的诸多领域，革命性地改变了这些领域内传统的研究和设计方法[1].但是CFD数值模拟的先天不足在于控制流动的偏微分方程组的可解性以及解的唯一性没有得到任何理论证明，因此CFD数值结果的可信度就非常值得关注.验证与确认(verificatio and validation,V&V)是评价CFD数值结果可信度的重要手段，验证的目的在于验证离散格式、数值方法、程序代码离散并求解控制方程的正确性；而确认的意义在于确认所求解的控制方程及边界条件真实地反映了实际物理流动问题.

二十世纪八九十年代，国外就开始对验证与确认的研究给予高度重视，并逐步开展相关研究工作.1998年，AIAA在总结之前工作的基础上发布了第一部系统阐述CFD验证与确认的指南[2].而国内在验证与确认方面起步较晚，2007年，国内学者建议在国内广泛开展验证与确认研究，以推动国内CFD可信度研究[3].

在CFD可信度研究中，验证工作可以采用精确解方法和制造解方法，结合网格收敛性测试研究微分方程的求解精度及精度阶.传统V&V通常采用精确解方法(method of exact solutions,MES)[45]，这种方法一般将流动控制方程的精确解与数值解进行比较.但是遗憾的是，复杂的非线性方程少有精确解，一般能得到的都是经过简化之后的方程解析解，而简化后的方程并不能完整地体现原控制方程中的各项，因此也不能研究相应项的数值特性以及验证代码的正确性.相反，制造解方法(method of manufactured solutions,MMS)[67]不寻找控制方程的精确解，而是人为制造一个解，并使之满足添加源项之后的修正控制方程.制造解不一定是真实物理解，而仅仅是为了研究与验证控制方程中各项的数值特性和计算精度而人为设计的，因而比精确解方法更具有实用性.

文献[5]总结出了多种利用精确解进行CFD代码验证的算例，如膨胀波、斜激波、不可压层流边界层、库埃特流动、Burgers方程等.在分析了制造解方法和精确解方法的优缺点之后，指出采用制造解方法进行代码验证和数值算法测试具有很高的准确性.

采用制造解方法和网格收敛性测试进行代码验证最早由Roache和 Steinberg[6]提出.Roache[78]在总结代码和计算方法验证的文章中强调,通过制造解方法和网格收敛性测试进行验证非常具有严谨性和说服力.2008年在Lisbon举办的第三届CFD Uncertainty Analysis Workshop[9]上要求首次参加研讨会的与会者必须对二维湍流近壁流动形式的制造解进行制造解方法的测试，这表明制造解方法作为代码验证和精度测试的手段已得到认可.

同时，国外利用制造解方法开展V&V工作已有很多.首先，一些学者将制造解方法应用到数值方法的代码验证中.在CFD领域，针对Euler方程[10]、RANS(Reynolds averaged Navier-Stokes)方程[11]及直接数值模拟(direct numerical simulation,DNS)[1213]、高阶方法[14]求解代码的验证，MMS方法均有相关应用.此外，MMS还成功应用于浸入边界法精度验证[15]，等离子体流动模拟代码验证[1617]，多相流动求解验证[1819]，化学非平衡流动数值模拟验证[20]等计算流体力学领域.一些In-house软件，如Wind-US[21]和Loci-CHEM[22]均通过了制造解方法的精度阶验证；Marshall[23]甚至基于MMS方法专门开发了针对代码验证的C++函数库.

其次，制造解方法在边界条件的验证中也得到应用[2426].如Bond等[24]通过制造解方法验证并辨别出了边界条件和梯度重构公式上的缺陷；又如Folkner等[25]也利用MMS方法和精确解方法对格点型和格心型有限体积法的各种边界条件进行了验证.

再次，采用制造解方法进行数值算法研究与测试也得到众多学者的广泛关注. 如 Katz和Sankaran[2728]利用MMS方法研究了非结构网格质量对格点型和格心型有限体积算法计算精度的影响.类似的，Diskin和Thomas[2930]通过MMS方法求解线性对流方程和泊松方程分别分析了网格类型和网格质量对无黏通量和黏性通量计算精度的影响.Vedovoto等[31]通过MMS方法研究了基于压力的有限体积格式的数值精度特征.一些新算法在提出之后，通常采用MMS方法对其代码正确性和算法精度进行验证和分析[32-33].

此外，针对制造解方法要在一系列网格上求得收敛解代价较大的问题，Burg和 Murali[34]提出了类似于 Taylor展开的残差型制造解精度分析方法.Brglez[35]也对原始的MMS方法提出改进，以提高方法的易用性和简洁性.除了在光滑流场中得到应用之外，MMS方法还被拓展到具有间断特征的流场求解验证中[3638].以上的综述表明，制造解方法作为验证与确认的重要手段已经广泛应用于代码验证、精度分析、边界条件验证等方面，并逐步得到发展和完善.

相较于国外的蓬勃发展，国内在MMS方法的研究和应用上与国外还有较大差距.王瑞利等[3940]较早开展了这方面的研究，但是要在国内真正推广使用制造解方法还需要更多工作.本文在实现一种标量制造解和分量制造解方法的基础上，通过将制造解方法精度测试结果与经典精确解(二维无黏等熵涡)精度测试结果进行对比，进一步证实了制造解精度测试方法的有效性，并重点将这两种制造解方法应用于非结构网格二阶精度有限体积离散方法的精度验证，对非结构有限体积离散方法中各种常用的梯度重构方法、对流通量格式、扩散通量格式进行了网格收敛性精度测试，得到了一些有指导意义的结论.

1 制造解方法

通常需要一个精确解进行测试离散格式的计算精度.但是大多数可压缩黏性流动的精确解都过于简单，不能完整地体现控制方程的所有项.为了解决这个问题，Roache和Steinberg[6]提出了制造解方法.

1.1 制造解方法理论

制造解方法的基本思路是选择任意的“制造解”代入原始的控制方程(如Navier-Stokes(NS)方程或者Euler方程等).一般情况下，制造解不能满足原始的控制方程，代入控制方程后，右端项不为零，可以将引入的右端项设为源项.因此，制造解可以理解为带源项的修正方程的精确解,如下所示

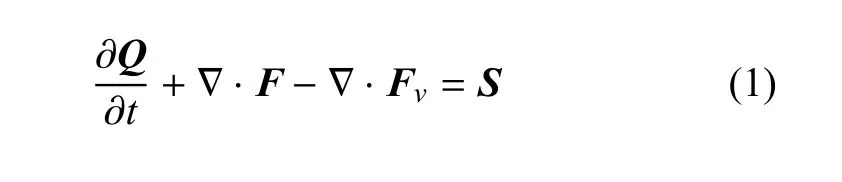
式中，Q为守恒变量，F=Fi+Gj+Hk为对流通量项，Fv=Fvi+Gvj+Hvk为扩散通量项.在离散网格上利用数值方法求解修正的控制方程，得到数值解，数值解与制造解的差值即为离散误差(不考虑舍入误差).结合网格收敛性测试便可以分析验证不同离散格式、计算方法的精度(或称误差)、数值精度阶以及代码编写的正确性.文献[27]指出,只要制造解源项的处理方式与控制方程的离散方法在数值精度上相容，MMS方法是评价数值格式特性的有效方法.

式(1)既可以针对标量模型方程进行制造解方法研究，也可以针对流动控制方程组进行制造解方法研究.对于标量模型方程，通常采用以下定义[28]

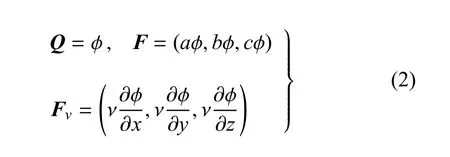
标量模型方程的最终形式为

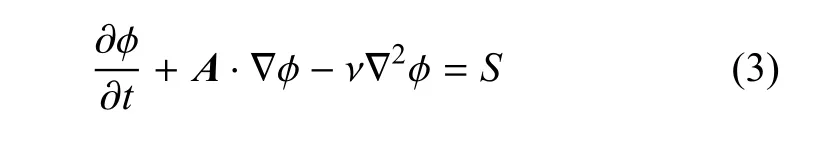
式中，φ为任意标量场，A=(a,b,c).可以看到,标量模型方程实质上是一个带源项的线性对流扩散方程.A和ν分别为线性对流项和线性扩散项的常系数.

而对于NS方程，方程(1)中各项可以表示为如下形式[28]

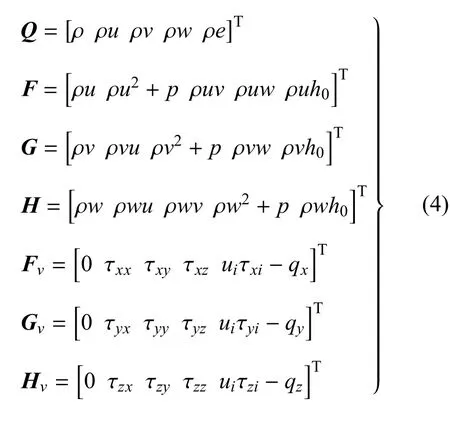
式中,ρ,u,v,w,e,h0,p分别为密度、3个速度分量、总能量、总焓和压强，此外τ和q分别为黏性应力张量和热传导矢量.

制造解方法进行精度验证可以总结为以下 6步[41]：(1)选择控制方程的形式；(2)选择制造解的形式；(3)推导修正后的控制方程；(4)在多套依次加密的网格上求解离散形式的修正控制方程得到数值解；(5)计算数值解的离散误差；(6)计算得到数值精度阶，进行精度分析和验证.

针对上述标量方程和NS方程，常用的制造解主要有标量制造解和分量制造解，以下给出文献[27-28,41]中所采用的几种制造解，制造解流场云图如图1所示.本文的研究仅采用式(6)和式(7)所示的Euler制造解进行测试验证工作；控制方程采用不考虑黏性项的Euler方程，以及标量对流扩散方程，不同测试算例采用的控制方程和制造解形式在算例中均有相应说明.制造解源项采用Mathematica数学软件进行公式推导精确求得，消除源项离散误差.

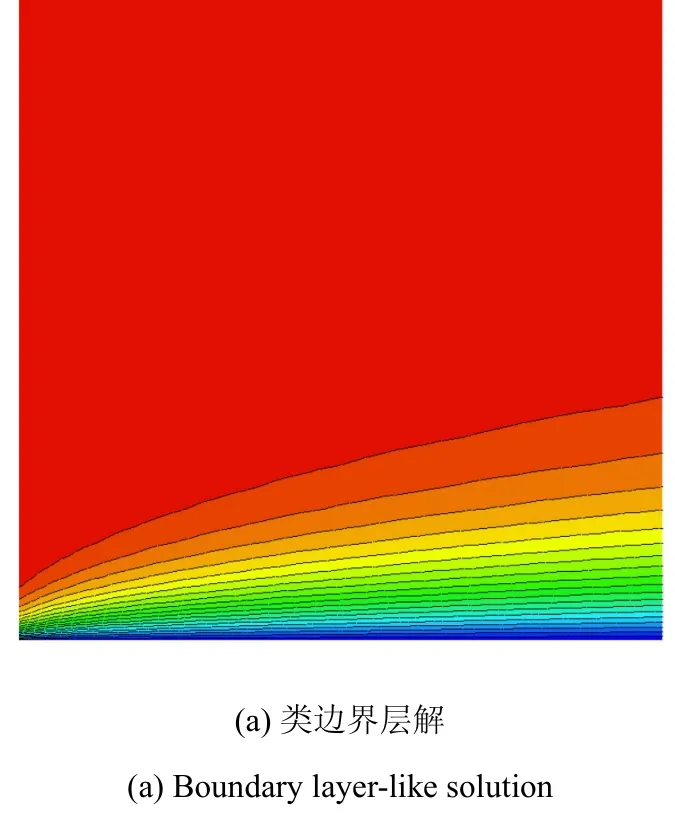
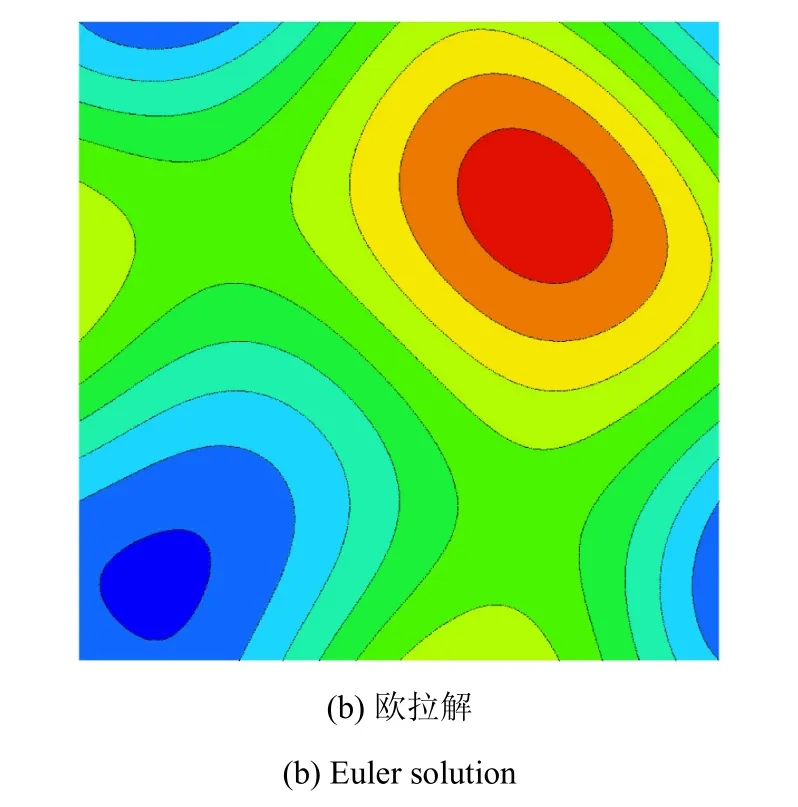
图1 两种类型的制造解流场云图Fig.1 Contours of two types of manufactured solutions

1.2 制造解方法验证

为了验证上一节中制造解精度测试方法的有效性，本节采用经典精确解——二维无黏等熵涡流动和Euler制造解方法对同一离散方法、同一网格在相同条件下进行精度对比验证.二维无黏等熵涡的初始流场由式(8)给出[42]，需要指出的是，等熵涡流动实质上是制造解的一个特例，其制造解源项为零.

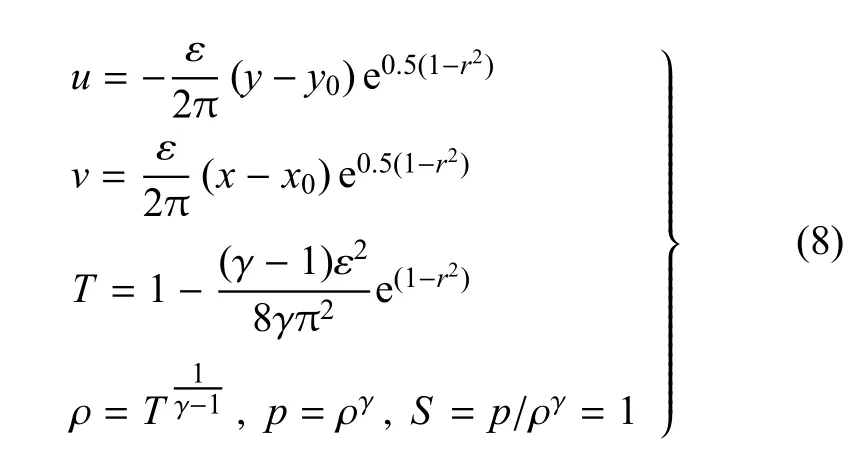
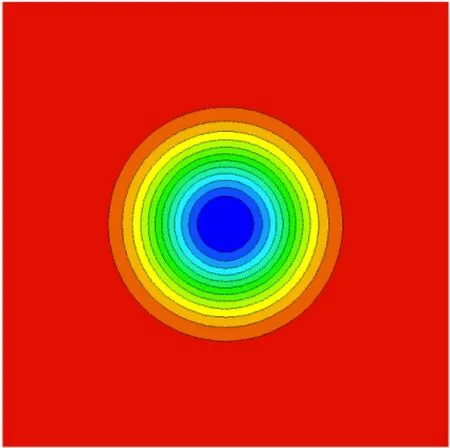
图2 二维无黏等熵涡流场云图Fig.2 Contour of a 2D inviscid isentropic vortex

分别在图 3所示的 4种网格上利用等熵涡流动、分量Euler制造解、标量Euler制造解对Euler方程和对流方程进行网格收敛性测试，得到离散方法的数值精度阶，并进行比较，结果如表1所示.关于数值精度阶的测试方法详见文献[43]，测试的计算平台为课题组自主研制的HyperFLOW软件[4445].

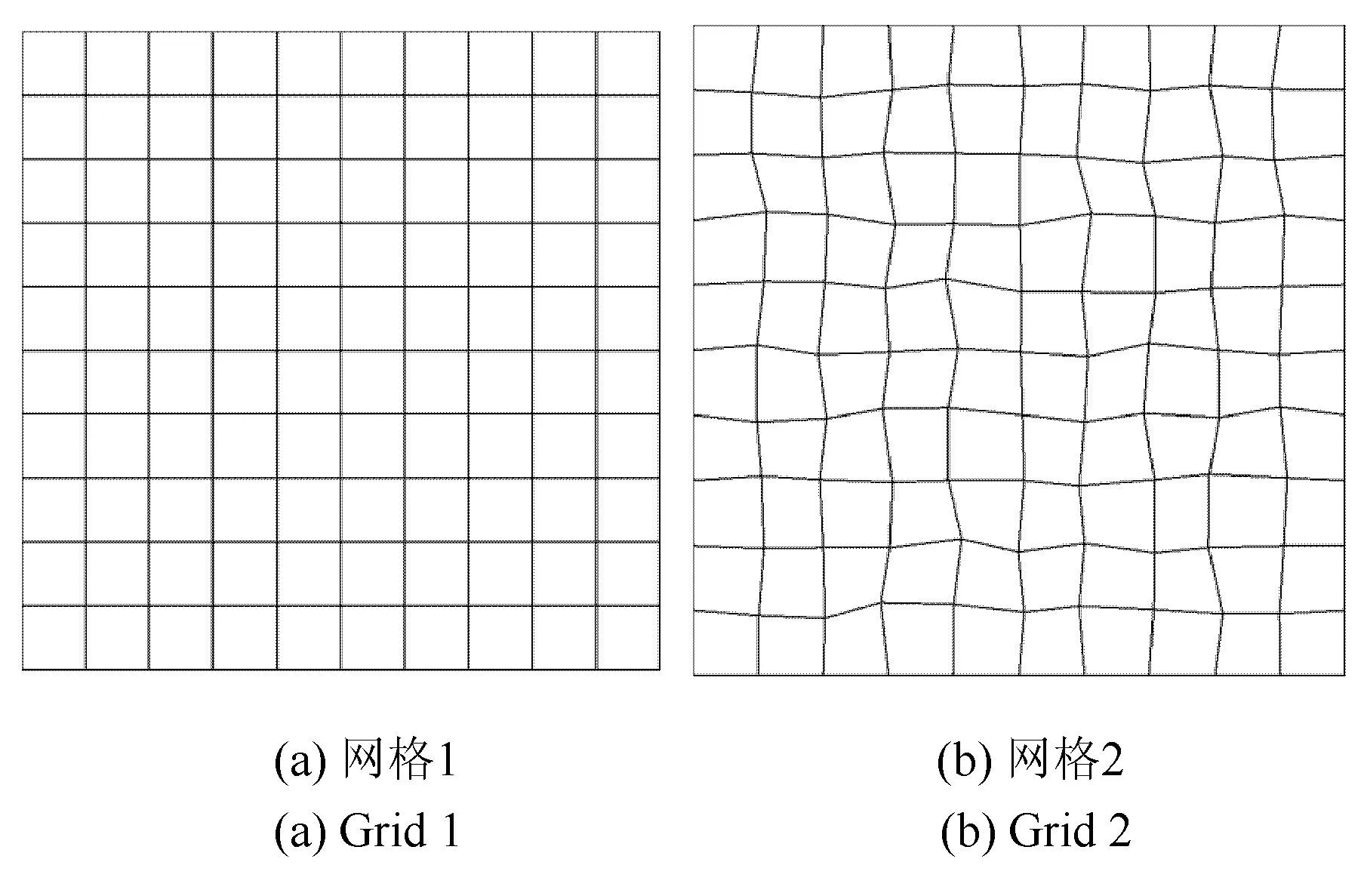
从表1可以看到，在4种不同类型的网格上，等熵涡流动精度测试、分量Euler制造解精度测试、标量Euler制造解精度测试得到的流动求解精度阶完全一致.这证实了前述的标量制造解方法和分量制造解方法是CFD方法验证有效工具的论断.需要说明的是，这里采用的是格心型非结构网格有限体积离散格式，流动变量的重构采用GG-Cell梯度重构方法[42,46]，对流通量离散采用Roe格式.利用其他方法也能得到制造解和精确解数值精度阶一致的结果.

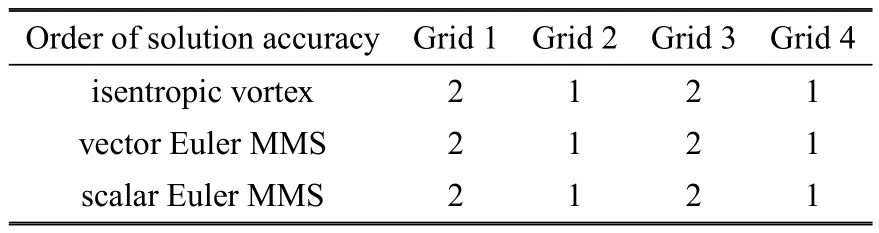
表1 制造解方法的验证Table 1 Verificatio of the MMS procedure

2 制造解方法在精度验证中的应用

在非结构网格有限体积离散格式中，基于梯度重构的迎风格式是最受欢迎的对流通量离散格式，如矢通量分裂格式：AUSM格式，Van Leer格式，Steger-Warming格式；通量差分分裂格式：Roe格式等.通常这些通量离散格式需要至少一阶精度的梯度重构以确保二阶精度的有限体积离散.

一般来说，在非结构网格上，通常有基于Green-Gauss(GG)公式的梯度重构方法和基于最小二乘(least squares,LSQ)的梯度重构方法.根据面心值求解方式的不同GG方法又可以分为4种,如表2所示[42].

表2 不同种类的GG梯度重构方法Table 2 Di ff erent types of GG gradient reconstruction methods

LSQ方法则根据是否加权、是否采用扩充模板又分为加权的最小二乘梯度重构WLSQ，不加权的最小二乘梯度重构LSQ，以及相应扩充模板(extended)或者基本模板 (basic)的 WLSQ和 LSQ方法[42,46]，如表3所示.

而扩散通量计算精度主要取决于控制体交界面梯度的计算方法.根据单元梯度值的加权方式、界面值是否连续、以及是否引入差分修正项，界面梯度的计算方法分为很多种[47].

表3 不同种类的LSQ梯度重构方法Table 3 Di ff erent types of LSQ gradient reconstruction methods

本文仅考虑两种非结构网格界面梯度求解方法，以说明制造解方法在验证扩散通量计算方法中的应用，这两种界面梯度的求解方法公式分别如式(9)～式(11)所示.

(1)Aver method取左右单元梯度的平均值.

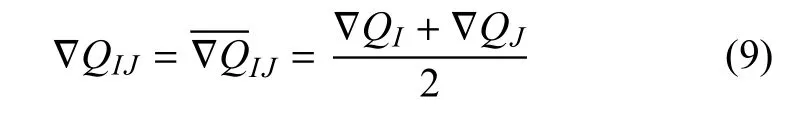
(2)Edge correction method[48]在取平均值的基础上，在相邻格心连线方向引入差分修正.

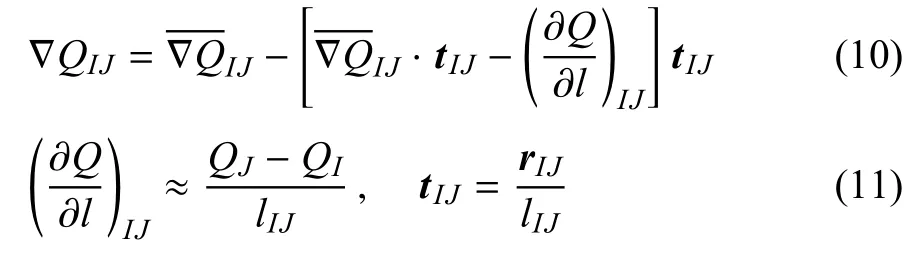
文献[48]指出,虽然aver method简单易实现，不需要额外的数据存储，但是会在四边形网格或六面体网格上导致奇偶失联，而edge correction method则能够在四面体、三棱柱及六面体网格上形成强耦合的模板，本文将从计算精度角度对这两种方法进行对比验证.

网格收敛性测试选取5套依次加密的网格，数值模拟制造解流动，边界条件为Dirichlet边界，消除边界条件离散的误差，测试离散误差随网格尺度减小时的收敛情况.通过密度离散误差的L1模随网格尺度(mesh size)的收敛结果来研究各种方法的模拟精度及数值精度阶.

2.1 单元梯度重构方法的验证

本节通过分量Euler制造解考察表2中4种GG方法，以及表3中的WLSQ-basic和WLSQ-extended方法在图3所示的4种网格上求解Euler方程的计算精度.对流通量采用Roe格式进行离散.

图4中曲线“1st”表示采用常量重构的流动模拟结果，即认为单元内流动变量为常数，单元界面左右状态直接取为左右单元的值，而不经过梯度重构得到；“1st order ref.”和 “2nd order ref.”分别代表一阶精度和二阶精度参考曲线，给出一阶精度和二阶精度曲线参考斜率，即离散误差下降的速率.

图4(a)和图4(c)显示，对于规则网格Grid 1和Grid 3，所有梯度重构方法在求解Euler方程时均能达到二阶精度，满足二阶有限体积法的预期.而图4(b)和图4(d)显示，在非规则网格Grid 2和Grid 4上，采用GG-Cell和GG-Node梯度重构方法会使流动模拟降阶到一阶，在同样的网格尺度下，流动模拟精度明显下降.因此梯度重构方法的选择对流动模拟精度有非常重要的影响，甚至决定了离散方法的精度阶，而精度阶直接反应了离散误差在网格加密时的下降速率.

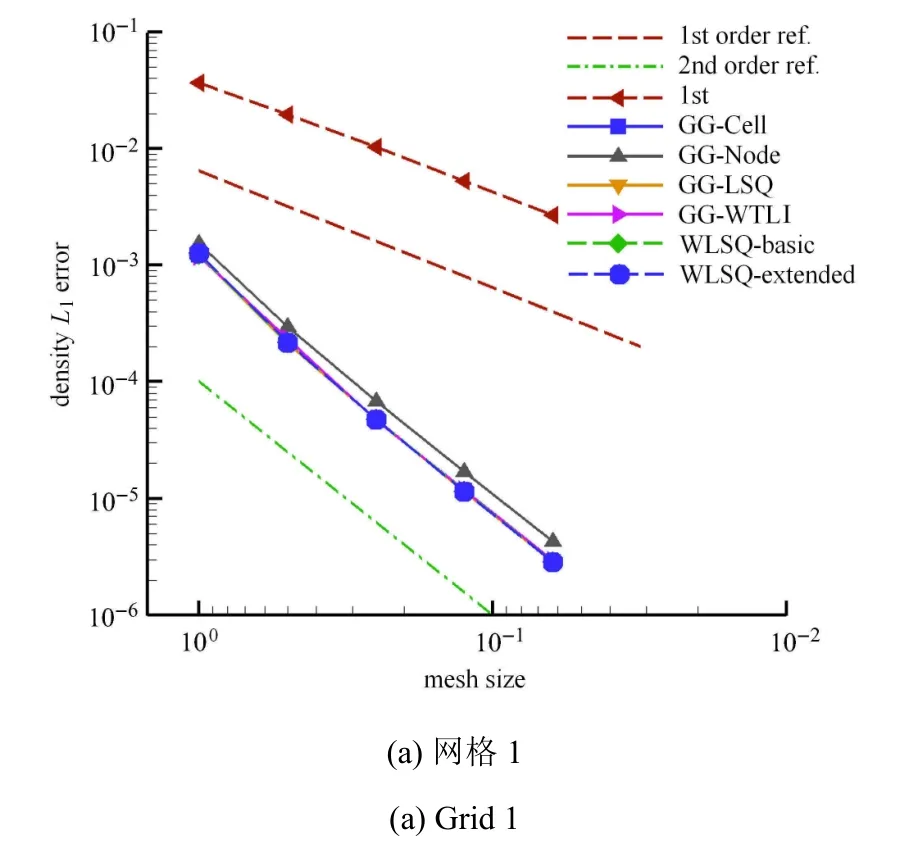
图4 不同梯度重构方法的分量Euler制造解精度测试结果Fig.4 Testing on di ff erent gradient methods with vector Euler MMS

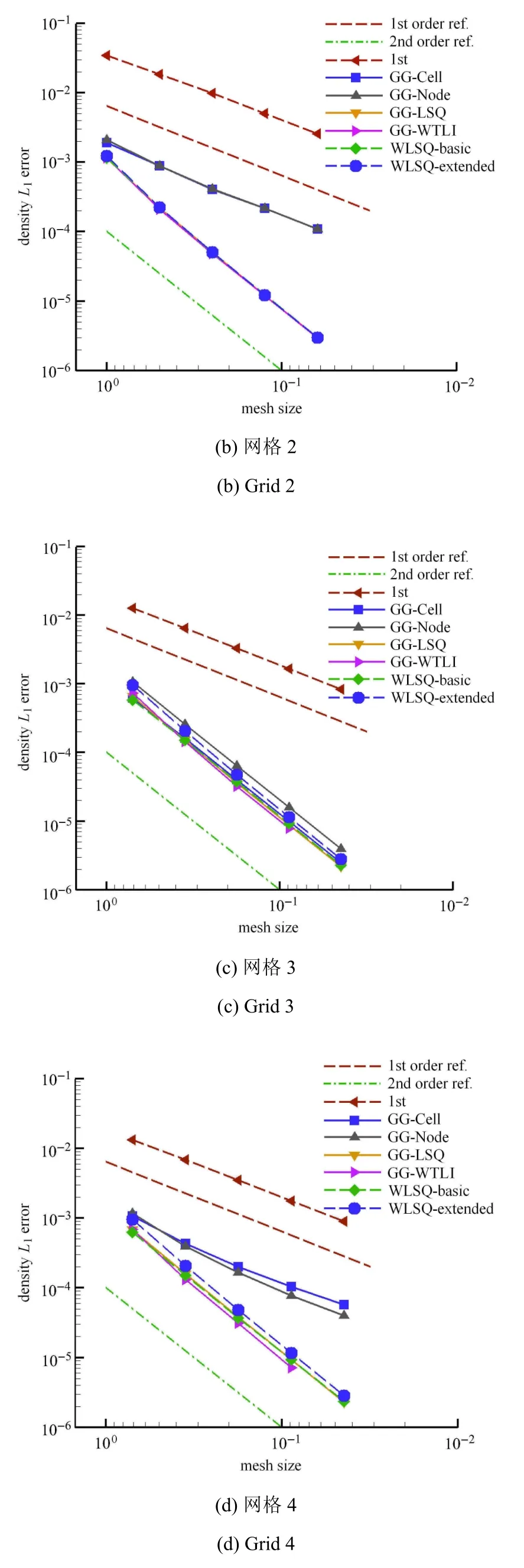
图4 不同梯度重构方法的分量Euler制造解精度测试结果(续)Fig.4 Testing on di ff erent gradient methods with vector Euler MMS(continued)

GG-Cell及GG-Node方法流动模拟精度降阶的原因在于在非规则网格上面心值插值未能达到二阶精度，导致梯度重构精度为0阶，从而导致流动模拟只有一阶精度，而其他能够保证面心值二阶插值精度的方法如GG-LSQ和GG-WTLI，以及LSQ方法均能保持梯度一阶精度，从而保证流动模拟的二阶精度，具体分析可参见文献[49].

2.2 对流通量离散的验证

本节通过分量Euler制造解考察4种对流通量格式(AUSM+,Roe,Steger-Warming,Van Leer)对Euler方程模拟精度的影响.

采用规则四边形网格Grid 1和非规则四边形网格Grid 2；单元梯度重构分别采用GG-Cell方法和WLSQ-basic方法，同样采用5套依次加密的网格，进行网格收敛性测试.

图5显示，不同的通量格式对流动模拟精度影响不大，各种通量格式离散误差非常接近.实际上，图5的结果再次证实梯度重构方法的选择是Euler方程模拟精度的主要影响因素，图5(a)和图5(b)显示,采用GG-Cell方法在规则和非规则网格上进行梯度重构出现了精度阶上的差异，而图5(c)和图5(d)显示,WLSQ-basic方法对网格是否规则并不敏感，各种对流通量均能保持二阶精度，且绝对误差相差很小.这与上一节中关于梯度重构方法的验证结论一致.

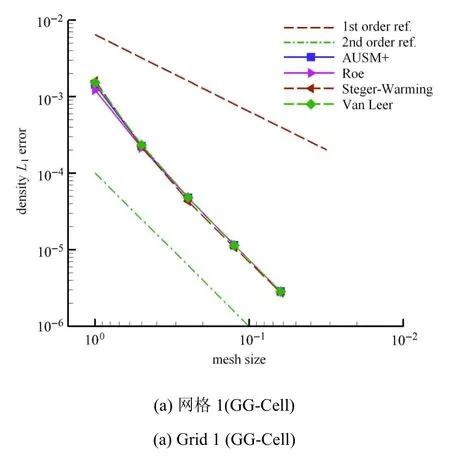
图5 不同通量格式的分量Euler制造解精度测试结果Fig.5 Testing on di ff erent inviscid flu schemes with vector Euler MMS

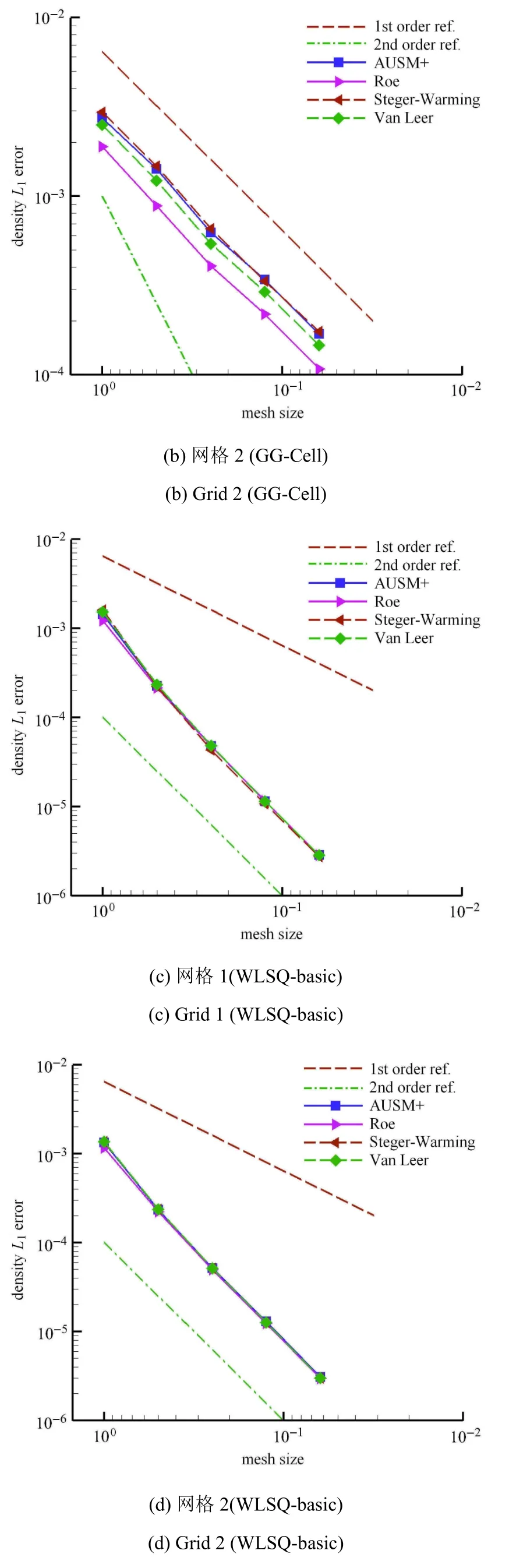
图5 不同通量格式的分量Euler制造解精度测试结果(续)Fig.5 Testing on di ff erent inviscid flu schemes with vector Euler MMS(continued)

2.3 扩散通量离散的验证

本节通过标量Euler制造解对标量扩散方程(方程(3)中取对流项系数 A=0)进行精度测试，验证不同界面梯度计算方法对扩散通量离散精度的影响.网格收敛性测试采用规则网格Grid 1和Grid 3，梯度重构分别采用GG-Cell方法和WLSQ梯度重构方法.需要说明的是，由于在扰动网格Grid 2和Grid 4上，网格扰动会导致GG-Cell方法单元梯度重构精度降阶到零阶[49]，从而引入单元梯度重构精度这一多余影响因素，故在此不考虑Grid 2和Grid 4.

图6显示，无论是规则四边形网格(Grid 1)还是规则三角形网格(Grid 3)，采用aver method求解界面梯度值都会导致标量扩散方程求解精度下降.如图6(a)和图6(c)所示，在Grid 1上，当界面梯度采用aver method时，流动模拟精度随着网格加密逐渐降阶到一阶；而图6(b)和图6(d)显示在Grid 3上，采用GG-Cell单元梯度重构的aver method会降阶到一阶，而采用WLSQ-basic单元梯度重构的aver method会降阶到零阶，离散误差显著增大.相反，采用edge correction method则在两种网格上，对于两种单元梯度重构方法(GG-Cell和WLSQ-basic)均能保证扩散方程求解的二阶精度，离散的绝对误差也明显比aver method更小.因此，扩散通量中界面梯度的计算方法对流动模拟精度有较大影响.而扩散方程求解精度降阶的原因还有待进一步分析.

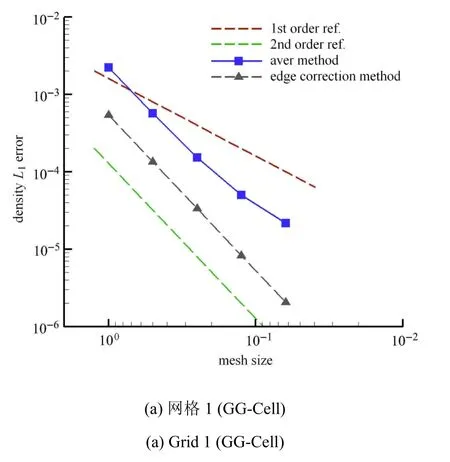
图6 不同界面梯度计算方法的标量Euler制造解精度测试结果Fig.6 Testing on di ff erent interface gradient methods with scalar Euler MMS

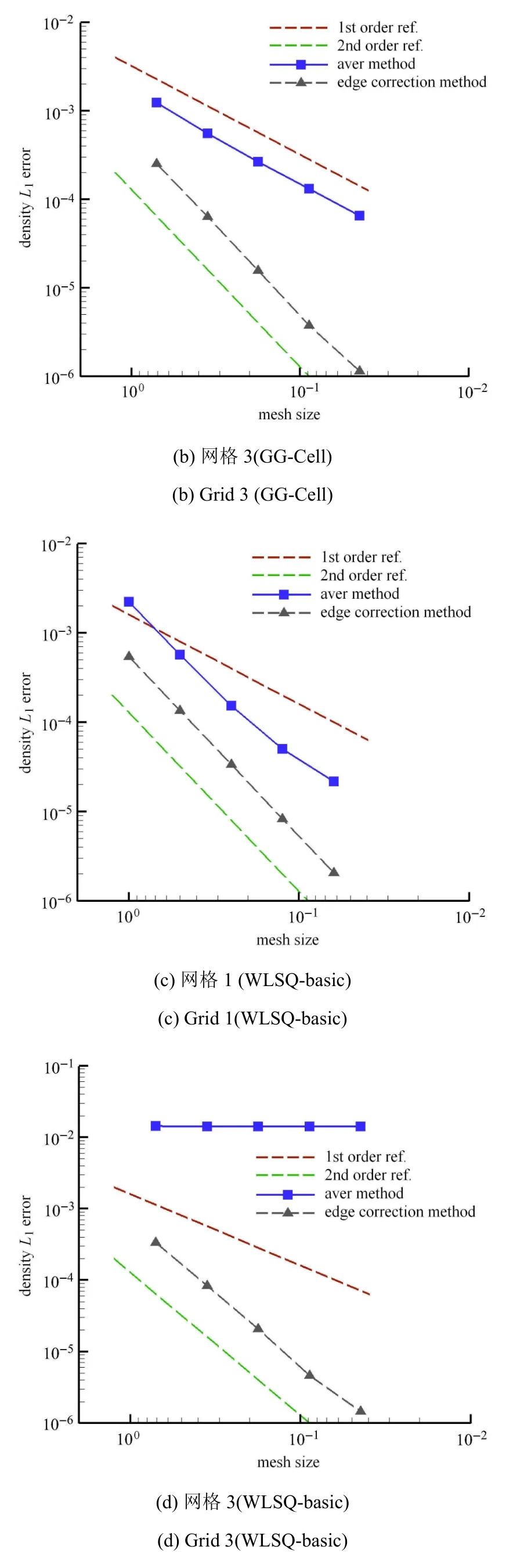
图6 不同界面梯度计算方法的标量Euler制造解精度测试结果(续)Fig.6 Testing on di ff erent interface gradient methods with scalar Euler MMS(continued)

3 结论

本文在实现一种分量制造解和标量制造解方法的基础上，通过将制造解精度测试结果与典型精确解算例——二维无黏等熵涡精度测试结果进行对比，进一步证实了制造解精度测试方法进行CFD方法和代码验证的可行性和有效性.

本文成功地将标量制造解和分量制造解应用于非结构网格梯度重构方法、对流通量格式、扩散通量格式的验证.结果表明,梯度重构方法的选择对Euler方程模拟精度有明显影响，在非规则网格上采用GG-Cell和GG-Node方法进行单元梯度重构会导致流动模拟精度降阶，离散误差明显增大，而LSQ方法则对网格是否规则并不敏感.本文选择的几种无黏通量格式均能够保持二阶精度，且各种格式的离散误差接近，说明在这种情况下，近似Riemann解的选取对计算结果精度的影响有限.而对扩散通量中界面梯度计算方法的验证结果显示，界面梯度计算方法对流动模拟精度有显著影响.

下一步工作将针对NS方程进行制造解方法的验证与确认工作；同时，边界条件的验证、各向异性网格上“黏性”制造解流动的模拟、以及扩散方程精度降阶的原因也是进一步研究的方向.

1阎超,于剑,徐晶磊等.CFD模拟方法的发展成就与展望.力学进展,2011,41(5)：562-589(Yan Chao,Yu Jian,Xu Jinglei,et al.On the achievements and prospects for the methods of computational flui dynamics.Advances in Mechanics,2011,41(5)：562-589(in Chinese))

2 Porter JL,Agarwal R,Azad RS,et al.Guide for the verificatio and validation of computational flui dynamics Simulations.AIAA G-077-1998,1998

3邓小刚，宗文刚，张来平等.计算流体力学中的验证与确认.力学进展,2007,37(2)：279-288(Deng Xiaogang,Zong Wengang,Zhang Laiping,et al.Verificatio and validation in computational flui dynamics.Advances in Mechanics,2007,37(2)：279-288(in Chinese))

4 Iannelli J.An exact non-linear Navier-Stokes compressible-fl w solution for CFD code verification International Journal for Numerical Methods in Fluids,2013,72(2)：157-176

5 GhiaU,BayyukS,RoyC,etal.TheAIAAcodeverificatio project-Test cases for CFD code verification AIAA Paper 2010-125,2010

6 Roache PJ,Steinburg S.Symbolic manipulation and computational flui dynamics.AIAA Journal,1984,22(10)：1390-1394

7 Roache PJ.Code verificatio by method of manufactured solutions.Transactions of ASME,2002,124(1)：4-10

8 Roache PJ.Verificatio of codes and calculations.AIAA Journal,1998,36(5)：696-702

9 Eca L,Hoekstra M,Roache PJ,et al.Code verification solution verificatio and validation：an overview of the 3rd Lisbon Workshop.AIAA Paper 2009-3647,2009

10 Maruli VK,Burg COE.Verificatio of 2D Navier-Stokes codes by the method of manufactured solutions.AIAA Paper 2002-3109,2002

11 Eca L.Klaij CM,Vaz G,et al.On code verificatio of RANS solvers.Journal of Computational Physics,2016,310：418-439

12 Silva HG,Souza LF,Medeiros MAF.Verificatio of a mixed highorder accurate DNS code for laminar turbulent transition by the method of manufactured solutions.International Journal for Numerical Methods in Fluids,2010,64(3)：336-354

13 Petri L,Sartori P,Rogenski J,et al.Verificatio and validation of a direct numerical simulation code.Computer Methods in Applied Mechanics and Engineering,2015,291：266-279

14 Navah F,Nadarajah S.On the verificatio of high-order CFD solvers//VII European Congress on Computational Methods in Applied Sciences and Engineering,Crete,Greece,June,2016

15 Brem C,Hader C,Fasel HF,A locally stabilized immerse boundary method for the compressible Navier-Stokes equations.Journal of Computational Physics,2015,295：475-504

16 Ricci P,Riva F,Theiler C,et al.Approaching the investigation of plasma turbulence through a rigorous verificatio and validation procedure：A practical example.Physics of Plasma,2015,22(5)：055704

17 Dudson BD,Madsen J,Omotani J,et al.Verificatio of BOUT++by the method of manufactured solutions.Physics of Plasma,2016,23(6)：062303

18 Choudhary A,Roy CJ,Dietiker J,et al.Code verificatio for multiphase fl ws using the method of manufactured solutions,International Journals of Multiphase Flow,2014,80：150-163

19 Brady PT,Herrmann M,Lopez JM.Code verificatio for finit volume multiphase scalar equations using the method of manufactured solutions.Journal of Computational Physics,2012,231(7)：2924-2944

20 Wang L,Zhou W,Ji C.Verificatio of a chemical non-equilibrium fl ws solver using the method of manufactured solutions.Procedia Engineering,2015,99：713-722

21 Nelson CC,Roy CJ.Verificatio of the Wind-US CFD code using the method of manufactured solutions.AIAA Paper 2004-1104,2004

22 Veluri SP,Roy CJ,S.Hebert,et al.Verificatio of the Loci-CHEM CFD Code using the Method of Manufactured Solutions.AIAA Paper 2008-661,2008

23 Marshall DD.A scientifi software verificatio library based on the method of manufactured solutions.AIAA Paper 2011-615,2011

24 Bond RB,Ober CC,Knupp PM,et al.Manufactured solution for computational fluidynamics boundary condition verification AIAA Journal,2007,45(9)：2224-2236

25 Folkner D,Katz A,Sankaran V.Design and verificatio methodology of boundary conditions for finit volume schemes.Computers and Fluids,2014,96：264-275

26 Choudhary A,Roy CJ,Luke EA,et al.Code verificatio of boundary conditions for compressible and incompressible flui dynamics codes.Computers and Fluids,2016,126：153-169

27 KatzA,SankaranV.Meshqualitye ff ectsontheaccuracyofCFDsolutions on unstructured meshes.Journal of Computational Physics,2011,230：7670-7686

28 Katz A,Sankaran V.High aspect ratio grid e ff ects on the accuracy of Navier-Stokes solutions on unstructured meshes.Computers&Fluids,2012,65：66-79

29 Diskin B,Thomas JL,Nielsen EJ,et al.Comparison of nodecentered and cell-centered unstructured finite-olume discretizations：viscous flu es.AIAA Paper 2009-0597,2009

30 Diskin B,Thomas JL.Comparison of node-centered and cellcentered unstructured finite-olume discretizations：inviscid flu es.AIAA Paper 2010-1079,2010

31 Vedovoto JM,Neto AS,Mura A,et al.Application of the method of manufactured solutions to the verificatio of a pressure-based finite volume numerical scheme.Computers and Fluids,2011,51：85-99.32 Blais B,Bertrand F.On the use of the method of manufactured solutions for the verificatio of CFD codes for the volume-averaged Navier-Stokes equations.Computers and Fluids,2015,114：121-129

33 Thorne J,Katz A.Source term discretization e ff ects on the accuracy of finit volume schemes.AIAA Paper 2015-0571,2015

34 Burg COE,Maruli VK.Efficient code verificatio using the residual formulation of the method of manufactured solutions.AIAA Paper 2004-2628,2004

35 Brglez S.Code verificatio for governing equations with arbitrary functions using adjusted method of manufactured solutions.Engineering with Computers,2014,30(4)：669-678

36 Grier B,Alyanak E,White M,et al.Numerical integration techniques for discontinuous manufactured solutions.Journal of Computational Physics,2014,278(c)：193-203

37 Grier B,Figliola R,Alyanak E,et al.Discontinuous solutions using the method of manufactured solutions on finit volume solvers.AIAA Journal,2015,53(8)：2369-2378

38 Woods CN,Starkey R.Verificatio of fluid-dynami codes in the presence of shocks and other discontinuities.Journal of Computational Physics,2015,294(c)：312-328

39王瑞利,林忠,袁国兴.科学计算程序的验证和确认.北京理工大学学报,2010,30(3)：353-360(Wang Ruili,Lin Zhong,Yuan Xingguo.Verificatio and validation in scientifi computing code.Transactions of Beijing Institute of Technology,2010,30(3)：353-360(in Chinese))

40余云龙,林忠,王瑞利等.辐射流体力学Lagrange方程组一类人为解构造方法.应用数学和力学,2015,36(1)：110-118(Yu Yunlong,Lin Zhong,Wang Ruili,et al.A method of manufacturing solutions for verificatio of Lagrangian Radiation hydrodynamics codes.Applied Mathematics and Mechanics,2015,36(1)：110-118(in Chinese))

41 Roy CJ.Review of code and solution verificatio procedures for computational simulation.Journal of Computational Physics,2005,205：131-156

42 Sozer E,Brehm C,Kiris CC.Gradient calculation methods on arbitrary polyhedral unstructured meshes for cell-centered CFD solvers.AIAA paper 2014-1440,2014

43 Hebert S,Luke EA,Honey I.A new approach to CFD verificatio studies.AIAA Paper 2005-685,2005

44 He Xin,Zhao Zhong,Ma Rong,et al.Validation of HyperFLOW in subsonic and transonic fl w.Acta Aerodynamical Sinica,2016，34(2)：267-275

45 He X,He XY,He L,et al.HyperFLOW：A structured/unstructured hybridintegratedcomputationalenvironmentformulti-purposeflui simulation.Procedia Engineering,2015,126：645-649

46 Mavriplis DJ.Revisiting the least-squares procedure for gradient reconstruction on unstructured meshes.AIAA Paper 2003-3986,2003

47 Jalali A,Sharbatdar M,Ollivier GC.Accuracy analysis of unstructured finit volume discretization schemes for di ff usive flu es.Computer and Fluids,2014,101：220-232

48 Haselbacher A,Blazek J.On the accurate and efficient discretization of the Navier-Stokes equations on mixed grids.AIAA Journal,2000,38(11)：2094-2102

49王年华,张来平,马戎等.非结构网格质量对梯度重构及无黏流动模拟精度的影响.计算力学学报,2017已录用(Wang Nianhua,Zhang Laiping,Ma Rong,et al.Mesh quality e ff ects on the accuracy of gradient reconstruction and inviscid fl w simulation on isotropic unstructured grids.Chinese Journal of Computational Mechanics,2017 to be published(in Chinese))

ACCURACY VERIFICATION OF UNSTRUCTURED SECOND-ORDER FINITE VOLUME DISCRETIZATION SCHEMES BASED ON THE METHOD OF MANUFACTURED SOLUTIONS1)

Wang Nianhua∗,2)Zhang Laiping∗,†Zhao Zhong∗He Xin∗,†∗(Computational Aerodynamics Institute，China Aerodynamics Research and Development Center，Mianyang 621000，Sichuan，China)†(State Key Laboratory of Aerodynamics，China Aerodynamics Research and Development Center，Mianyang 621000，Sichuan，China)

With the great improvement in computer technology,computational flui dynamics have progressed signifi cantly.Even though it is fast and easy to obtain discretized results via numerical simulations,the validity and accuracy of the results need to be carefully validated and verified As an important approach in verificatio and validation,the method of manufactured solutions(MMS)was widely applied in code verification accuracy analysis and verificatio of boundary conditions.This paper firs established the procedures for the MMS with scalar manufactured solutions and vector man-ufactured solutions.Verificatio of these two procedures was performed by comparing results of accuracy testing for a typical exact solution(2D inviscid isentropic vortex).The MMS procedures were then employed to the study of unstructured finite-olume discretization schemes,such as gradient reconstruction methods,convective flu es discretization and di ff usive flu es discretization.It demonstrated that some schemes employing certain Green-Gauss based gradient degrade to 1st order on irregular meshes and discretization error increases significantl,while the least squares based gradient is insensitive to mesh irregularity.Besides,all tested convective flu es discretization schemes were 2nd order accurate and they exhibited similar performance in terms of accuracy.But the method of computing the interface gradient was an essential factor a ff ecting the accuracy of di ff usive flu es discretization.

verificatio and validation,method of manufactured solutions,method of exact solutions,grid convergence study,finit volume discretization,numerical accuracy

V211.3

：A

10.6052/0459-1879-16-260

2016–09–18 收稿，2017–02–25 录用,2017–02–25 网络版发表.

1)国家自然科学基金资助项目(11532016).

2)王年华,硕士研究生,主要研究方向：计算流体力学,有限体积离散方法.E-mail：nianhuawong@126.com

王年华,张来平,赵钟,赫新.基于制造解的非结构二阶有限体积离散格式的精度测试与验证.力学学报,2017,49(3)：627-637

Wang Nianhua,Zhang Laiping,Zhao Zhong,He Xin.Accuracy verificatio of unstructured second-order finit volume discretization schemes based on the method of manufactured solutions.Chinese Journal of Theoretical and Applied Mechanics,2017,49(3)：627-637