椭圆曲线y2=px(x2-32)的正整数点

朱 萍,饶丽梅,杜先存

(红河学院教师教育学院，云南 蒙自 661199)

椭圆曲线y2=px(x2-32)的正整数点

朱 萍,饶丽梅,杜先存

(红河学院教师教育学院，云南 蒙自 661199)

目的 椭圆曲线的整数点是数论中的一个重要问题。设p是素数，椭圆曲线y2=px(x2±a),a∈Z+的整数点问题是椭圆曲线的一个重要问题。但是p为奇素数时，关于椭圆曲线y2=px(x2-32)的整数点问题至今仍未解决。方法 利用四次Diophantine方程的已知结果，运用唯一分解定理、奇偶数的性质、同余的性质、Legendre符号的性质等初等方法。结果 证明p≡5(mod8)为奇素数时，椭圆曲线y2=px(x2-32)至多有2个正整数点。结论 研究结果对于p是素数时，椭圆曲线y2=px(x2±a),a∈Z+的求解有一定的借鉴作用，同时推进了该类椭圆曲线的研究。

椭圆曲线；正整数点；同余；奇素数；Legendre符号

在数论和算术代数几何学中，椭圆曲线的正整数点一直以来都是一个基本而又重要的问题，关于椭圆曲线y2=px(x2±b)(p,b∈Z+)的正整数点问题，已有的主要结论为：b=1时的情形，文献[1]～[4]已给出了相关的一些研究；b=2时的情形，文献[5]～[9]已给出了相关的一些研究；b=4时的情形，文献[10]～[11]已进行了一些研究；b=64时的情形，文献[12]～[13]已进行了一些研究。关于b=32的情况目前还未有相关结果。本文利用初等方法对p≡5(mod8)为奇素数时椭圆曲线y2=px(x2-32) 的整数点的情况进行了研究，得出了如下结论：

定理 如果p≡5(mod8)为奇素数，则椭圆曲线

y2=px(x2-32)

(1)

至多有2个正整数点。

1 相关引理

引理1[14]a,b∈Z+，则方程ax4-by2=1至多有2组正整数解。

2 定理证明

证明：设(x,y)是椭圆曲线(1)的整数点，因为p≡5(mod8)为奇素数，故由(1)知p|p， 设y=pz，z∈Z+,将其代入(1)，得

pz2=x(x2-32)

(2)

因为gcd(x,x2-32)=gcd(x,32)=1或2或4或8或16或32，故(2)式可分解为以下12种情形：

情形Ix=a2,x2-32=pb2,z=ab,gcd(a,b)=1,a,b∈Z+;

情形IIx=pa2,x2-32=b2,z=ab,gcd(a,b)=1,a,b∈Z+;

情形IIIx=2a2,x2-32=2pb2,z=2ab,gcd(a,b)=1,a,b∈Z+;

情形IVx=2p2a,x2-32=2b2,z=2ab,gcd(a,b)=1,a,b∈Z+;

情形Vx=4a2,x2-32=4pb2,z=4ab,gcd(a,b)=1,a,b∈Z+;

情形VIx=4pa2,x2-32=4b2,z=4ab,gcd(a,b)=1,a,b∈Z+;

情形VIIx=8a2,x2-32=8pb2,z=8ab,gcd(a,b)=1,a,b∈Z+;

情形VIIIx=8pa2,x2-32=8b2,z=8ab,gcd(a,b)=1,a,b∈Z+;

情形IXx=16a2,x2-32=16pb2,z=16ab,gcd(a,b)=1,a,b∈Z+;

情形Xx=16pa2,x2-32=16b2,z=16ab,gcd(a,b)=1,a,b∈Z+;

情形XIx=32a2,x2-32=32pb2,z=32ab,gcd(a,b)=1,a,b∈Z+;

情形XIIx=32pa2,x2-32=32b2,z=32ab,gcd(a,b)=1,a,b∈Z+。

下面分别讨论这12种情形下椭圆曲线(2)的正整数点的情况，即讨论这12种情形下椭圆曲线(1)的正整数点的情况。

情形I：

由x=a2,x2-32=pb2, gcd(a,b)=1知gcd(x,x2-32)=1， 故x为奇数，x2-32也是奇数。 又p≡5(mod8)为奇素数，则由(2)式知z为奇数，故a、b均为奇数。

将x=a2代入x2-32=pb2，得a4-32=pb2,两边取模8得

a4≡pb2(mod8)

(3)

因为a、b均为奇数， 有a4≡1(mod8)，b2≡1(mod8)。又p≡5(mod8)为奇素数， 所以(3)式为1≡5(mod8)， 此式显然不成立，故该情形椭圆曲线(1)无正整数点。

情形II：

由x=pa2,x2-32=b2, gcd(a,b)=1知gcd(x,x2-32)=1， 所以x为奇数，x2-32也是奇数。 又p≡5(mod8)为奇素数， 则由(2)式知z为奇数，故a,b均为奇数。

由x2-32=b2, 得x2-b2=32, 即

(x+b)(x-b)=32

(4)

(4)式解得(x,b)=(±9, 7), (±6, 2),由x=pa2, 得pa2=9或6， 与“p≡5(mod8)为奇素数”矛盾， 故该情形椭圆曲线(1)无正整数点。

情形III的讨论：

将x=2a2代入x2-32=2pb2, 得4a4-32=2pb2, 即

2a4-16=pb2

(5)

(5)式两边取模8， 得2a4-16≡pb2(mod8)。 又p≡5(mod8)为奇素数， 故由(5)式知b为偶数， 所以b2≡0, 4(mod8), 因此pb2≡0, 4(mod8)。 又gcd(a,b)=1, 而b为偶数， 所以a为奇数， 于是有a4≡1(mod8), 所以(5)式为2≡0, 4(mod8), 即1≡0, 2(mod8)， 显然不成立， 故该情形椭圆曲线(1)无正整数点。

情形IV：

将x=2pa2代入x2-32=2b2, 得2p2a4-16=b2, 可知b为偶数，b=2c，c∈Z+, 代入2p2a4-16=b2， 得

p2a4=2c2+8

(6)

因为p≡5(mod8)为奇素数，b为偶数且gcd(a,b)=1，故a为奇数， 所以(6)式左边p2a4为奇数， 右边2c2+8为偶数， 等式显然不成立， 故该情形椭圆曲线(1)无正整数点。

情形V：

将x=4a2代入x2-32=4pb2, 得4a4-8=pb2， 两边同时取模p， 得

4a4≡8(modp)

(7)

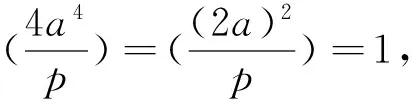
情形VI：

将x=4pa2代入x2-32=4b2, 得4p2a4-8=b2， 两边同时取模p， 得

-8≡b2(modp)

(8)

情形VII：

将x=8a2代入x2-32=8pb2, 得8a4-4=pb2， 两边同时取模p， 得

8a4≡4(modp)

(9)

情形VIII：

将x=8pa2代入x2-32=8b2得

8p2a4-4=b2

(10)

由(10)式知2|b, 令b=2c,c∈Z+代入(10)式， 得2p2a4-1=c2， 即

2p2a4-c2=1

(11)

由引理1知， 方程(11)至多有2组正整数解， 故该情形椭圆曲线(1)至多有2个正整数点。

情形IX：

将x=16a2代入x2-32=16pb2, 得16a4-2=pb2， 两边同时取模p， 得

16a4≡2(modp)

(12)

情形X：

将x=16pa2代入x2-32=16b2, 得16p2a4-2=b2， 两边同时取模p， 得

-2≡b2(modp)

(13)

情形XI：将x=32a2代入x2-32=32pb2, 得32a4-1=pb2， 两边同时取模p， 得

32a4≡1(modp)

(14)

情形XII：

将x=32pa2代入x2-32=32b2, 得32p2a4=b2+1， 两边同时取模8, 得

32p2a4≡b2+1(mod8)

(15)

因为p≡5(mod8)为奇素数， 由(15)知为奇数， 有b2≡1(mod8)。 则(22)为0≡2(mod8), 显然不成立， 故该情形椭圆曲线(1)无正整数点。

综上,定理得证。

[1]窦志红.椭圆曲线y2=2px(x2+1)上正整数点的个数[J].纯粹数学与应用数学，2011,27(02)：210-212+235.

[2]祝辉林,陈建华.两个丢番图方程y2=nx(x2±1)[J].数学学报,2007,50(05):1071-1074.

[3]乐茂华.椭圆曲线y2=px(x2±1)的正整数点[J].湛江师范学院学报,2008,29(03):1-2.

[4]赵院娥.椭圆曲线y2=2px(x2-1)的正整数点的个数[J].西安石油大学学报,2012,27(02):106-107+110.

[5]陈历敏.Diophantine方程y2=px(x2+2)[J].数学学报，2010,53(01)：83-86.

[6]廖思泉，乐茂华.椭圆曲线y2=px(x2+2)的正整数点[J].数学杂志，2009,29(03)：387-390.

[7]李玲，张绪绪.椭圆曲线y2=nx(x2+2)的整数点[J].西安工程大学学报，2011,25(03)：407-409.

[8]李润琪,刘霄.椭圆曲线y2=nx(x2-2)的整数点[J].河北北方学院学报(自然科学版),2016,32(03):10-11+20.

[9]赵晶晶.椭圆曲线y2=px(x2-2)的整数点[J].湖北民族学院学报(自然科学版),2016,34(01):40-41+59.

[10]崔军保.椭圆曲线y2=px(x2+4)的正整数点[J].佳木斯大学学报，2014,32(06)：962-963.

[11]万飞.椭圆曲线y2=nx(x2-4)的整数点[J].湖北民族学院学报(自然科学版),2015,33(03):271-272.

[12]崔保军.椭圆曲线y2=px(x2+64)的正整数点[J].甘肃高师学报，2015,20(02)：7-9.

[13]赵晶晶.椭圆曲线y2=px(x2-64)的整数点[J].唐山师范学院学报,2016,38(02):17-19.

[14]袁平之，张中锋.丢番图方程ax4-by2=1[J].数学学报，2010,53(03)：443-454.

[责任编辑：关金玉 英文编辑：刘彦哲]

Positive Integral Points on Elliptic Curvey2=px(x2-32)

ZHU Ping,RAO Li-mei,DU Xian-cun

(College of Teacher’s Education,Honghe University,Mengzi,Yunnan 661199,China)

Objective The integral points on elliptic curve is a very important problem of Number Theory.Letpbe a prime, the integral points on elliptic curvey2=px(x2±a),a∈Z+isaveryimportantproblemofellipticcurve.Whenpis an odd prime, the integral points on elliptic curvesy2=px(x2-32)tillremainsunresolved.Methods In this paper,some known results of quartic Diophantine equation were used to obtain our results.The elementary methods were used including the properties of Legendre symbol，the properties of even number and odd number,the properties of congruence and unique decomposition.Results It was proved that ifpis an odd prime andp≡5(mod8),then there are at most two positive integer points the elliptic curve in title.Conclusion These results can help solve the integral points on elliptic curvey2=px(x2±a),a∈Z+，withpas an odd prime,and these results promote the study of the kind of elliptic curve.

elliptic curve;positive integer point;congruence;odd prime;Legendre symbol

云南省教育厅科研基金项目(2014Y462)；红河学院科研基金项目(XJ15Y22)；红河学院大学生科技创新项目(SZ1651)

朱萍(1995-)，女，云南保山人，红河学院2013级小理专业在读学生。

杜先存(1981-)，女，副教授，硕士研究生，研究方向：数论及数学教育。

F

A

10.3969/j.issn.1673-1492.2017.05.001

来稿日期：2016-09-22