应用VMD和多参数融合的齿轮箱故障诊断*

安邦，潘宏侠，张媛，张玉学，赵雄鹏(.中北大学机械与动力工程学院，太原03005;.中国电子科技集团公司第二研究所，太原03004)

应用VMD和多参数融合的齿轮箱故障诊断*

安邦1，潘宏侠1，张媛2，张玉学1，赵雄鹏1
(1.中北大学机械与动力工程学院，太原030051;2.中国电子科技集团公司第二研究所，太原030024)

由于齿轮箱故障信号的非线性，以及各种噪声的影响导致故障特征难以确定，为了准确、高效地分析齿轮箱故障信号，提出了一种应用变分模态分解(VMD)和多参数融合的齿轮箱故障诊断方法。首先对齿轮箱故障信号进行变分模态分解，并与传统的经验模态分解(EMD)进行对比;同时提取各模态分量的能量百分比和信息熵作为特征值，并采用RBF神经网络进行故障诊断。实验结果表明变分模态分解能够有效避免模态混叠现象的发生，以VMD为基础的多参数融合方法能够准确、快速地实现齿轮箱的故障诊断。

多参数融合;齿轮箱;故障诊断

0 引言

当齿轮箱发生故障时，常用的故障诊断方法是通过采集振动加速度信号进行分析，然而由于齿轮箱的振动响应是各个频率特征信息的叠加，因此就需要通过滤波和信号分解提取特征值进行故障诊断。传统的经验模态分解(EMD)算法存在模态混叠问题，需要进一步优化，为此程军圣［1］等人将局部特征尺度分解(LCD)引入到齿轮箱故障诊断中，刘述文［2］等将局域均值分解(LMD)应用在齿轮箱故障诊断中，虽然均取得不错的效果，但还没有从根本上解决问题;Konstantin Dragomiretskiy［3］于2014年提出了变分模态分解(VMD)方法，该方法能够将复杂信号自适应地分解为K个调幅-调频信号，有效抑制模态混叠现象［4］。因此，为了准确、高效地提取故障特征，避免模态混叠的干扰，本文尝试将VMD方法引入到齿轮箱故障诊断领域，并结合信息熵理论与神经网络对齿轮箱进行故障诊断。

1 实验方案设计

选取JZQ250减速齿轮箱作为实验对象，为了模拟齿轮箱在现实环境中的工作状态，将三相异步电动机Y280-M4作为动力源对齿轮箱进行驱动，在齿轮箱的输出端联接磁粉制动器，以提供实验过程中的负载，将故障设置在中间轴，分别设置五种工况分别是:正常状态、故障一断齿、故障二轴承外圈断裂故障、故障三轴承内圈点蚀故障以及故障四保持架断裂故障。故障设置如图1所示。

图1 故障设置

在齿轮箱轴承上对应的箱盖位置对称安装6个CA-YD系列的压电式加速度传感器，设置采样频率为5120 Hz，通过LMS系统对采集的时域信号滤波和放大，每种工况采集8组原始信号储存备用，实验平台装置原理图如图2所示。

图2 齿轮故障诊断实验装置

2 变分模态分解

2.1 VMD原理与算法

VMD方法的整体框架是变分问题，它使得分解后每个模态分量的带宽之和最小［5］。为了估算分量的带宽，首先对每个模态函数进行Hilbert变化，得到其单边频谱;然后加入一个预估中心频率e－jωkt，将每个分量的频谱变换到基带上;最后计算解析信号梯度的平方L2范数，估计各模态分量带宽［6］。

假设经过VMD分解之后，原始信号被分解为K个模态分量，则变分约束模型为:

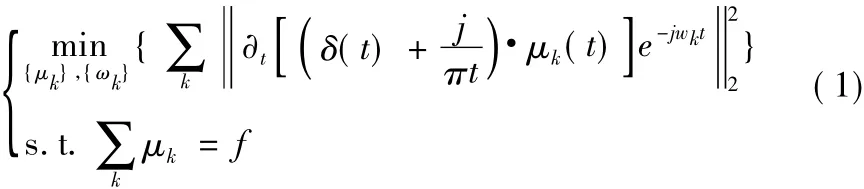
式中，μk表示各模态分量的合集，ωk表示各中心频率的合集，δ(t)表示单位脉冲函数。

为了解决上述变分约束模型，在VMD算法中引入二次惩罚项α和拉格朗日乘子λ。VMD具体实施步骤如下:

(2)令n=n+1，执行循环过程;

(3)令k=0，k=k+1，更新μk和ωk;

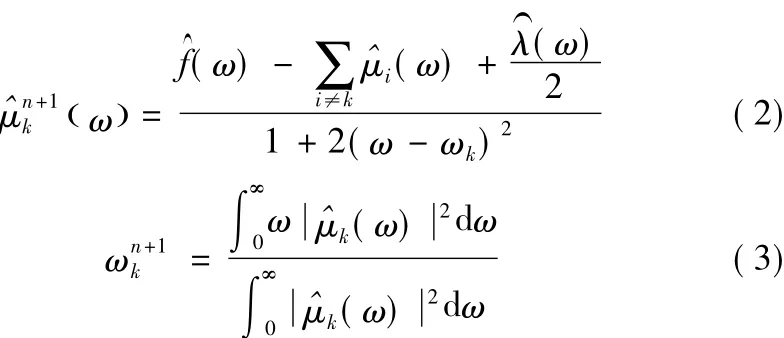
(4)更新λ:

2.2 模态混叠

模态混叠是指一个模态分量中包含差异极大的特征时间尺度(欠分解)，或者相近的特征时间尺度分布在不同的模态分量中(过分解)，表现为相邻两个模态分量波形混叠，相互影响难以分辨［7］。VMD可实现信号频域内各个分量的自适应剖分，有效避免EMD分解过程中的模态混叠现象，为了对比两种算法在抗模态混叠方面的性能，以采集到断齿故障信号为例，同时进行EMD分解和VMD分解，并对分解后的模态分量做频谱分析。在VMD分解过程中，当设置模态数k=5时出现中心频率相近的模态分量，即认为产生了过分解现象，因此选取模态数k=4;EMD分解中采用前四个分量作为参考，分解结果如图3所示。

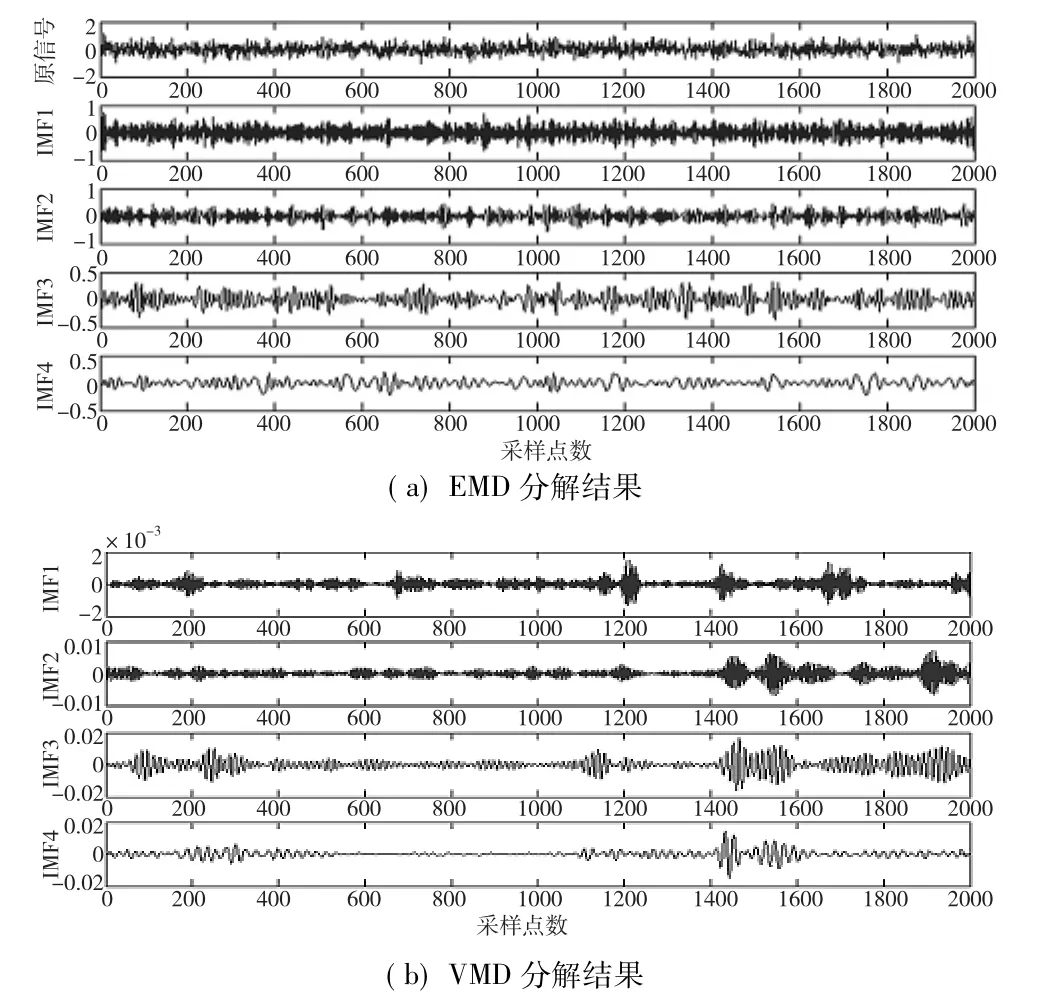
图3 VMD和EMD分解结果对比

计算各模态分量的互相关系数，选取VMD分解中的所有模态分量和EMD分解中的前四个模态分量做频谱分析，结果如图4所示。

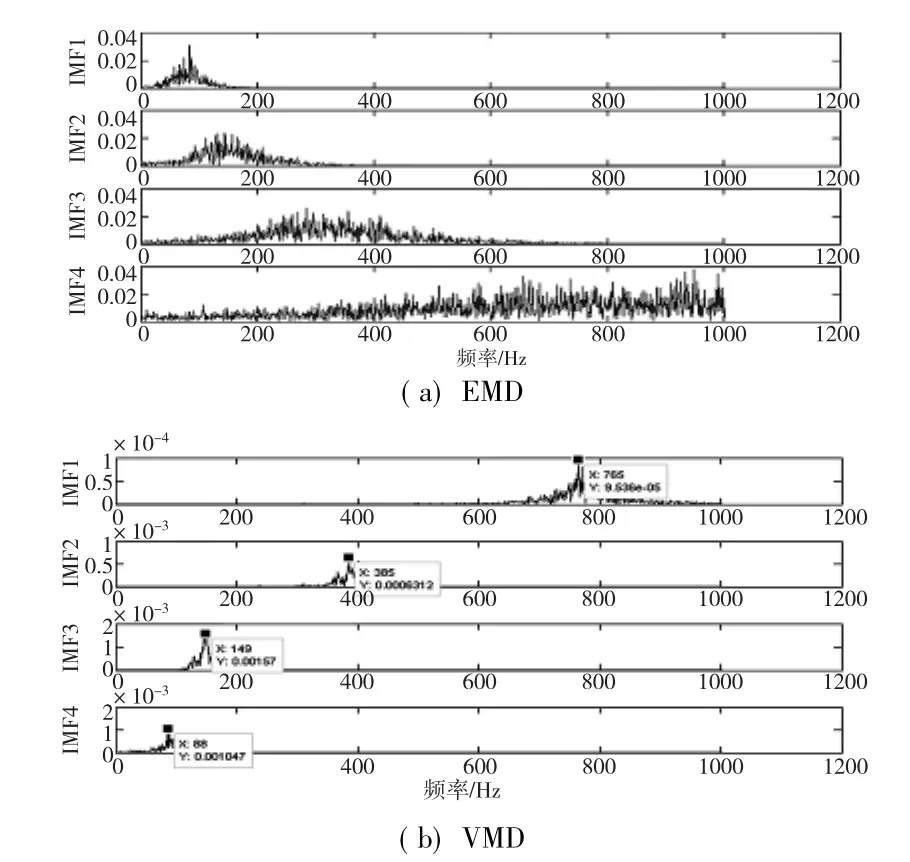
图4 分解后各模态的频谱图

可以看出，相对于VMD分解，EMD分解存在明显的模态混叠现象，因此，VMD分解更适合处理齿轮箱故障信号。

3 多参数融合

3.1 各分量能量百分比

在齿轮箱运行过程中，如果发生故障，那么相应的产生的振动信号经过VMD分解后各个模态分量的能量分布也会相应的变化，因此可以在VMD分解的基础上，研究每个模态分量的能量分布变化，并将各分量能量百分比值作为所需要的特征值进行提取，各分量能量百分比提取公式如下所示。

式中:e(i)表示第i个分量的能量百分比;E(ci)表示第i个分量的能量。

3.2 信息熵

齿轮箱在故障工况下的振动信号与正常工况相比，携带了很多微弱信息量，为了描述故障信号中携带的微弱信息量，引入了信息熵的概念。熵是信息论中事件出现概率不确定性的度量，它能反映事件包含的信息［8］。王金东［9］等人已经证明信息熵对信号具有良好的分类能力并能反映故障信号的复杂程度，因此将信息熵作为特征参量对故障诊断十分有效。

奇异谱熵用来表征信号能量在奇异谱划分下的不确定性，可以有效表示信号在时域的能量变化，计算步骤如下:

(1)将VMD分解后得到的n个IMF分量组成特征向量矩阵［c1，c2，…，cn］T;

(2)通过奇异值分解得到特征矩阵奇异值λi; (3)计算奇异谱熵:

功率谱熵用来表征振动能量在频域的分布状况，它能反映振动谱型的分布，它的计算步骤如下:

(1)对经过VMD分解后得到的每个IMF分量进行傅里叶变换;

(2)计算IMF分量傅里叶变换后的功率谱Si;

(3)计算功率谱熵:

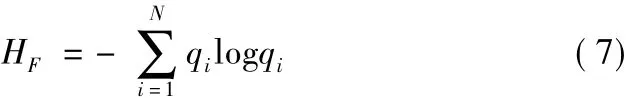
式中:qi=Si/S为第i个IMF分量功率谱占全部功率谱的比重。

齿轮箱在不同工作状态下的时频分布往往存在很大不同，为了定量描述这种变化程度引入时频熵概念。将总能量为A时频平面等分N个时频块，每块能量为Wi(1≤i≤N)，对每块能量进行归一化，得到δi= Wi/A，最终得到信号时频熵［10］:

特征提取过程如图5所示。

图5 特征提取流程图

将各IMF分量所占的能量和VMD信息熵共同作为特征值，组成40×7的特征矩阵，由于数据过于庞大，给出部分特征值如表1所示。

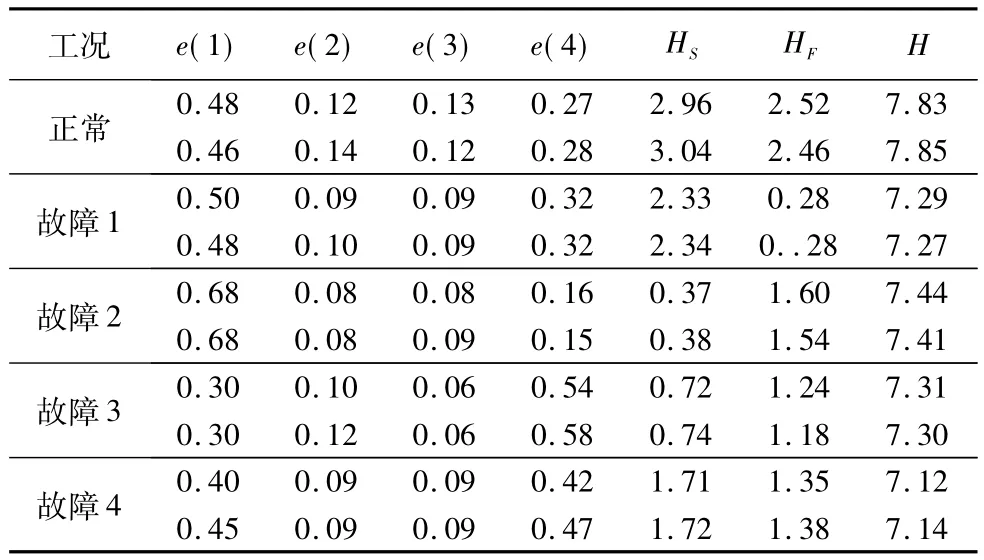
表1 部分特征值

4 RBF神经网络

4.1 RBF神经网络分类原理

RBF神经网络是一种新颖高效的前馈神经网络，由输入层、隐含层、输出层3层构成，其中输入层节点的作用是用来传输输入信号到隐含层节点，隐含层由径向基函数神经元组成，其作用是转化输入层到隐含层数据之间的非线性映射关系，将低维的模式输入数据转换到高维空间内，以利于输出层进行分类识别［10］。隐含层中基函数采用性能优异的径向对称高斯函数，其定义为:

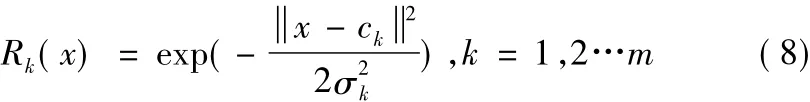
式中，Rk(x)为输出;x为输入向量;ck为中心向量;σk为高斯函数的方差。RBF神经网络的学习过程可以分为两个阶段，首先，根据所有的输入样本决定隐含层各节点类高斯函数的中心值ck以及标准化常数σk，当确定了隐含层的参数之后，再根据样本利用最小二乘法原则求出输出层的权值向量Wj［11］，它的训练模型如图6所示。

图6 RBF神经网络训练模型

4.2 故障识别

将提取出的特征值分成两个大组:每种工况的前四组数据被用作训练集，剩余四组数据被用作测试集，先对训练集进行训练，再对测试集进行测试，分类结果如图7所示。

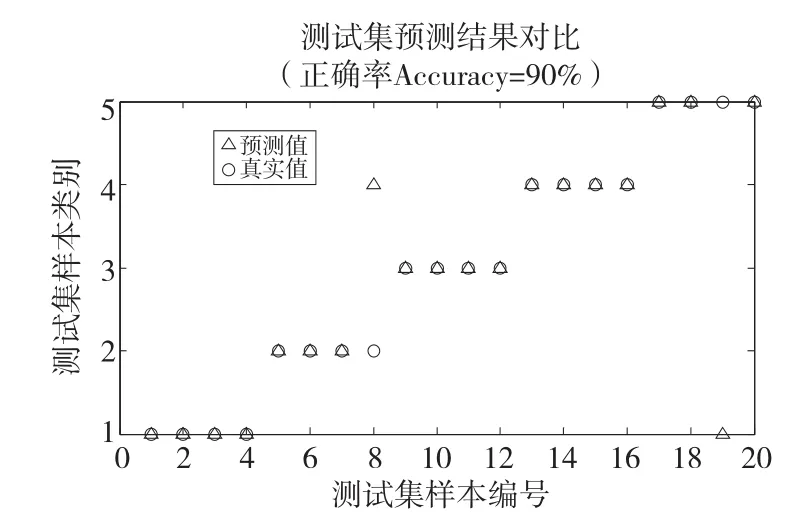
图7 分类结果

由图中分类结果可知，RBF神经网络对齿轮箱故障分类效果十分明显，分类准确率达到90%。

5 结论

采用VMD方法对齿轮箱振动信号进行分解，并与EMD方法进行对比，之后提取各模态分量的能量百分比和信息熵作为特征值输入到RBF神经网络中进行故障诊断，最终得到如下结论:

(1)变分模态分解在处理非线性、非平稳信号时可以有效避免模态混叠现象的发生，对齿轮箱故障信号具有更好的分解效果;

(2)将各分量的能量百分比和信息熵共同作为特征值能够全面准确地反映齿轮箱故障信息，结合RBF神经网络，可以快速、准确地实现齿轮箱的故障分类。

［1］程军圣，杨怡，杨宇.局部特征尺度分解方法及其在齿轮箱故障诊断中的应用［J］.机械工程学报，2012，48(9):64－71.

［2］刘述文，潘宏侠，刘涛涛.基于LMD和RBF结合的齿轮箱故障诊断［J］.机床与液压，2015，43(7):181－184.

［3］Dragomiretskiy K，Zosso D.Variational Mode Decomposition［J］.IEEE Tran on Signal Processing，2014，62(3):531－544.

［4］唐贵基，王晓龙.参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用［J］.西安交通大学学报，2015，49 (5):73－81.

［5］刘长良，武英杰，甄成刚.基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断［J］.中国电机工程学报，2015，35(13):3358－3365.

［6］陈立军，张海勇，韩东.基于VMD和HSA的水声跳频信号时频分析方法［J］.科学技术与工程，2015，15(28):165－169.

［7］王畅.基于HHT的微网电能质量检测与分析［D］.保定:华北电力大学，2014.

［8］龚萍，张辉，毛征，等.融合局部熵二维熵的空中目标跟踪算法研究［J］.国外电子测量技术，2014，33(1):32－35.

［9］王金东，代梅，夏法峰，等.基于EMD信息熵和支持向量机的往复压缩机轴承故障诊断［J］.流体机械，2014，34 (1):43－46.

［10］马廉洁，曹小兵，陈小辉，等.基于GA与RBF神经网络的工程陶瓷点磨削表面硬度数值模拟［J］.组合机床与自动化加工技术，2015(1):30－33.

［11］梁小晓，曹莉，韦崇岗，等.物联网感知层传感节点故障诊断研究［J］.组合机床与自动化加工技术，2015(3):62－66.

(编辑李秀敏)

Research on Gearbox Fault Diagnosis Based on VMD and Multi-parameter Fusion

AN Bang1，PAN Hong-xia1，ZHANG Yuan2，ZHANG Yu-xue1，ZHAO Xiong-peng1
(1.School of Mechanical and Power Engineering，North University of China，Taiyuan 030051，China;2.The 2nd Research Institute of China Electronics Technology Group Corporation，Taiyuan 030024，China)

Because of the non-linearity of the gearbox fault signal，and the influence of various noises，it is difficult to extract the fault features of the gearbox.In order to analyze the fault signal accurately and efficiently，a method based on Variational Mode Decomposition(VMD)and multi-parameter fusion is proposed.Firstly，the VMD decomposition of faultsignalis performed and compared with EMD decomposition results;Meanw hile，the energy percentage of each component is extracted and the information entropy of each sample is taken as the eigenvalue.Then the extracted feature parameters are input to the RBF neural netw ork for faultdiagnosis.The results show ed thatthe variationalmode decomposition can effectively avoid the phenomenon of modal mixture.The multi-parameter fusion method based on VMD can realize the fault diagnosis of gearbox accurately and quickly.

multi-parameter fusion;gearbox;fault diagnosis

TH17;TG65

A

1001－2265(2017)04－0092－04

10.13462/j.cnki.mmtamt.2017.04.023

2016－12－19;

2017－01－16

国家自然科学基金:基于粒子群优化和滤波技术的复杂传动装置早期故障诊断研究(50875247)

安邦(1993—)，男，河北石家庄人，中北大学硕士研究生，研究方向为装备系统检测诊断与控制，(E－mail)anbang0519@163.com;潘宏侠(1950—)，男，辽宁大连人，中北大学教授，博士生导师，研究方向为信息处理与识别、装备系统检测诊断与控制，(E－mail)panhx1015@163.com。