主轴热误差的改进累积法建模研究*

袁江，周成一，庄丽阳，邱自学，高传耀(.南通大学机械工程学院，江苏南通609;.南通第五机床有限公司，江苏南通666)

主轴热误差的改进累积法建模研究*

袁江1，周成一1，庄丽阳1，邱自学1，高传耀2
(1.南通大学机械工程学院，江苏南通226019;2.南通第五机床有限公司，江苏南通226661)

为提高机床的加工精度，针对主轴热误差建模，结合最小二乘原理和F分布检验提出了一种改进的累积新算法。对一台立式加工中心，采用激光位移传感器和分布的温度传感器同步测量主轴热变形及温度变化;对获取的建模数据，结合方差分析和F分布检验确定累积阶次K的最小值，在提高热误差建模精度的同时降低算法的复杂度;并进行累积算子求和，构建K(＞N+1)阶累积方程组，再运用最小二乘原理得出K阶累积广义均值的正规方程组，最后通过矩阵求解实现回归建模及参数估计。最后，对机床变工况条件下主轴热误差进行了实验与建模预测。结果表明:改进累积法的建模精度高于普通累积法，同时保证了建模效率。

主轴;热误差;累积法;建模

0 引言

近年来，随着机床制造水平的快速发展，机床主轴发热导致的变形问题成为影响加工精度的主要原因［1-2］。为有效控制热误差以提高机床加工精度，国内外学者进行了大量的研究，在热误差建模方法上提出了灰色理论、神经网络、最小二乘支持向量机［3-4］等多种算法，这些算法有的精度较高但建模时间长，有的建模精度不够理想、鲁棒性差，因此还需要寻求高效率、高精度的建模算法以适应现场热误差补偿的需要。

累积法具有简单、直观，不直接处理模型的误差项等特点［5-6］，其建立的模型可以保证平均误差为零，绝对误差最小。袁江［7］等人成功将其运用到主轴热误差建模上，且建模精度、建模效率相比较传统的最小二乘法已经有所改善。但该方法在应用中也存在以下两个主要问题:①普通累积法采用K=N+1的累积阶次，其建模精度比最小二乘法没有显著改善;②随着累积阶次K的增加，建模精度虽有提高，但计算量增加、建模效率下降［8］。

为提高机床主轴热误差建模的精度和效率，本文提出一种改进的累积新算法，先通过方差分析和F分布检验确定最小的累积阶次K，在保证建模精度有显著提高的同时降低算法的复杂度;然后构造K(＞N+1)个累积方程，利用补偿性减小随机误差的影响［9-10］，根据最小二乘原理求解正规方程得出热误差模型，并将该模型与普通累积法模型进行了建模精度与效率的对比分析。

1 改进累积法

具体建模算法如下:

(1)设(Xj1，Xj2…Xjn)，j=1，2…m为n个温度测点的温度序列，(Yj)，j=1，2…m为位移测点的位移数据，则热误差样本数据为(Xj1，Xj2…Xjn;Yj)，j=1，2…m。

(2)设累积回归模型为:

(3)通过方差分析和F分布检验选取最小的累积阶次K:

采用单侧检验，当F＜F0.95(υ1，υ2)时，此时模型的残余标准差的减小程度达到了α=0.05的显著性水平，选用此时的K确立模型。

(5)根据K阶累积和，结合最小二乘原理，构建K(＞N+1)阶累积方程组，使方程数大于未知量数:

(6)根据累积广义均值将累积方程组转化成矩阵形式:

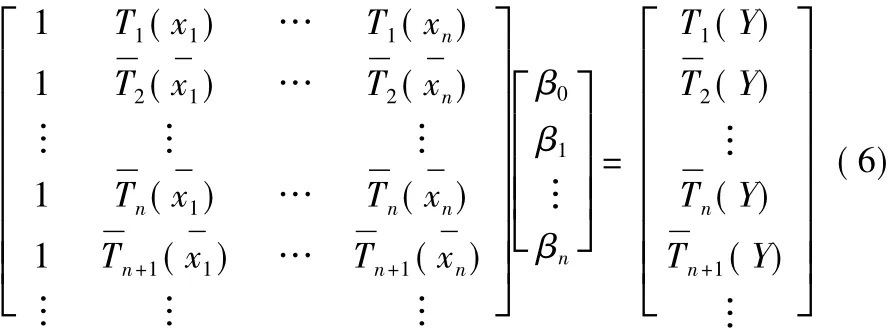
(7)根据最小二乘原理，设珔Ti(x珋1)=x1i，珔Ti(x珋2)= x2i…珔Ti(x珋n)=xni;珔Ti(Y)=yi，将累积正规方程中的系数作为数据源输入最小二乘法求解，并得出最小二乘正规方程:

(8)按矩阵形式求解，则正规方程解的矩阵表达式为:

将式(9)带入式(8)中求解，实现建模与参数估计:

2 热误差测试与建模

图1 热误差测试系统

2.1 机床热误差测试

选取一台VMC1060数控机床为被测对象，测试系统如图1所示，其中，分布的温度传感器测量机床主轴热敏区域内温度信息，而激光位移传感器测量主轴轴向的变形;上位机对温度传感器及激光位移传感器同步发送命令，并将接收的温度、热位移信息实时显示存储。测试时，每隔3min采集一次各测点温度x和热位移y，共采集43组数据［11-12］。测试结果如图2所示。

图2 热误差测试结果

2.2 建模算法程序设计

在图形化开发软件LabVIEW平台上开发了专用的改进累积回归建模算法程序，其流程如图3所示。

图3 改进累积法建模流程图

2.3 最小累积阶次K的选取

构建热误差回归模型之前需要确定累积矩阵阶数K和热误差样本容量m，由于本热误差实验选取两个热敏测点进行测试，即热误差方程的自变量为温度x1和温度x2，且各含有43组数据，因此有:

根据累积法性质矩阵X(k)与X具有相同的秩，得ran(X(k))=ranX=3，所以首先取K=4(＞2+1)，m=43。然后，对热误差样本的k阶累积和进行计算以构建出累积矩阵:

由X(k)≠0得X(k)为非奇异矩阵，因此，可构建热误差正规方程Y(k)=X(k)β，在LabVIEW中的运行结果如图4所示。

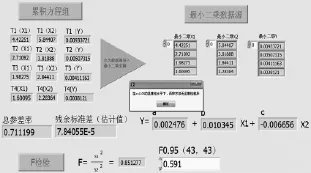
图4 改进累积法(K=4)建模结果

由程序计算结果得K=4(＞2+1)时，回归模型下的残余标准差σ22=7.84×10(－5)，与K=3(=2+1)时，普通累积法的残余标准差σ21= 9.21×10(－5)比较，并进行F检验，得F=0.851＞F0.95(43，43)=0.591，可知K=4时的改进累积法对模型精度有所提高，但并未达到α=0.05的显著性水平。

增大累积阶次，使K=5(＞2+1)并进行回归建模，经过程序运行可知，K=5时的改进累积法对模型精度有所提高，但仍未达到α=0.05的显著性水平。

故继续增大累积阶次。直至K=8(＞2+1)时，从图5可以看出，基于改进累积算法(k=8)的热误差模型为y=0.00790x1－0.00469x2+0.00173。经过F检验可知F=0.589＜F0.95(43，43)=0.591，即其残余标准差的减小已经达到了α=0.05的显著性水平，得到的建模结果见图5。因此选用k=8时的改进累积法模型。

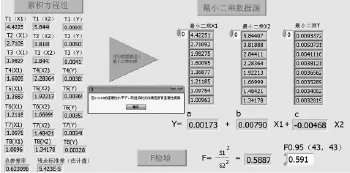
图5 改进累积法(k=8)建模结果

3 建模算法对比分析

分别采用改进累积法和普通累积法对机床热误差测试数据进行了建模，如图5、图6所示，并对模型预测值、样本几何中心、残余标准差以及效率指标进行了对比分析。

3.1 模型预测值

通过对比模型预测值，可十分直观、清晰地表现出各模型预测值的变化趋势，能否有效跟随实际热误差以及围绕实际热误差的波动幅度。两种算法的各模型预测值与实际值对比效果如图7所示。

图6 普通累积法建模结果

图7 各模型预测值与实际测量值对比效果

从图7不难看出，①无论机床是否达到热平衡状态，改进累积法模型的预测效果均为最优，能有效跟随机床热误差的变化趋势，其预测值基本围绕实测值分部，且波动幅度较小;②普通累积法模型在机床未达到热平衡状态时，预测结果和实际情况偏差较小。随着温度不断升高，直到机床基本处于热平衡状态时，其预测精度反而有所下降，和改进累积法模型的稳定性相比仍有一定差距。

3.2 样本几何中心

设(xj1，xj2，…xjn;Yj)，j=1，2…m为给定的样本，(x珋1，…x珋n;珔Y)为其几何中心。故为验证模型的可靠性，对样本几何中心(x1，x2，Y)分别采用改进累积法和普通累积法对几何中心估计值进行计算，公式为:

结果得改进累积法估计值为0.009324，普通累积法估计值为0.009313，计算误差忽略不计，说明改进累积法所得的回归模型与普通累积法基本一致。

3.3 残余标准差

采用残余标准差作为模型精度评价指标，结果如表1所示。其中残余标准差计算公式为:

其中:yi和i分别为实际值与预测值，m为样本数，n为自变量数。

表1 建模精度对比结果

由表1可以看出，改进累积法的建模精度最优，和普通累积法相比，建模精度得到显著提高。

3.4 建模效率

在提高建模精度的同时，降低算法的复杂度，保证建模效率同样是算法关注的重点，各算法建模效率如表2所示。

表2 建模效率对比结果

由表2可以看出，改进累积法与普通累积法相比，模型构建时间相当，建模效率并未有较大下降。因此，改进累积法较普通累积法，在提高建模精度的同时，保证了高效的建模效率。

4 结论

结合最小二乘原理和方差F分部检验，提出一种改进的累积新算法，并以某型号立式加工中心为实验对象，对其建立了主轴轴向热误差预测模型。比较分析了改进累积法模型和普通累积法模型对主轴轴向热误差的预测效果，可以得到如下结论:

(1)改进累积法既保留了普通累积法简单、直观、不直接处理模型误差项等特点，也解决了其累积阶次K的选取问题，在保证建模效率的基础上，进一步提高了热误差补偿模型的预测精度;

(2)对VMC1060数控机床进行改进累积法建模试验，取得了良好的预测效果，并与普通累积法进行了模型对比分析。结果表明，改进累积法模型建模精度指标有显著提高，建模时间低于2s，为后续的热误差实时补偿提供了良好的基础。

［1］M Gebhardt，J Mayr，N Furrer，et al.High precision greybox model for compensation of thermal errors on five-axis machines［J］.CIRP Annals-Manufacturing Technology，2014，63(1):509－512.

［2］赵昌龙，于淼.数控机床主轴热误差预测模型的修正［J］.组合机床与自动化加工技术，2014(7):100－102.

［3］张毅，杨建国.基于灰色理论预处理的神经网络机床热误差建模［J］.机械工程学报，2011，47(7):134－139.

［4］刘杨，蒋庆，桑迎平.最小二乘支持向量机在动态称重系统中的应用［J］.仪表技术与传感器，2013(12):170－172.

［5］崔旭冉，霍国栋，郑笑雪.基于累积法理论的弹性阻抗参数提取［J］.CT理论与应用研究，2015，24(2):177－188.

［6］路璐.基于普通累积法的经济预测［J］.北京工业职业技术学院学报，2013，12(4):65－68.

［7］袁江，周成一，邱自学，等.机床主轴热误差的累积法建模研究［J］.组合机床与自动化加工技术，2016(8):129－132.

［8］曹定爱.累积法理论［M］.北京:科学出版社，2011.

［9］费业泰.误差理论与数据处理［M］.北京:机械工业出版社，2010.

［10］Peng X J，Cai Y，Li Q.The least-squares method based on coupling coefficients for reactor power distribution reconstruction.Annals of Nuclear Energy，2016，94(8):272－278.

［11］袁江，沈亚峰，吕晶，等.机床热误差的RFID传感标签测试系统设计［J］.组合机床与自动化加工技术，2016 (3):108－111.

［12］吕晶，袁江，刘传进，等.高速高精密立式加工中心主轴热态特性分析［J］.组合机床与自动化加工技术，2014 (10):13－16.

(编辑李秀敏)

Modeling Research on Machine Tool Spindle Thermal Error Based on Improved Cumulative Method

YUAN Jiang1，ZHOU Cheng-yi1，ZHUANG Li-yang1，QIU Zi-xue1，GAO Chuan-yao2
(1.School of Mechanical Engineering，Nantong University，Nantong Jiangsu 226019，China;2.Nantong No.5 Machine Tool Company Ltd，Nantong Jiangsu 226661，China)

To improve the accuracy and efficiency of machine toolthermalerror modeling，a new improved cumulative method w as proposed by using the leastsquares method and F distribution test.For a verticalmachining center，the temperature and thermal deformation of spindle were measured simultaneously by using distributional temperature sensors and laser displacement sensor.The minimum value of cumulative order K was determined by using variance analysis and F distribution test，which can not only improve thermal error modeling accuracy，but also reduce the complexity of algorithm.Cumulative operator sum and K(＞N+1) order cumulative equations were built，and then the normalequations of K order cumulative generalaverage were obtained based on the principle of least squares.Regression modeling and parameter estimation w ere realized by using the matrix calculation.Finally，the thermal error on machine tool spindle under the changing w orking condition w as calculated and the results show that the modeling accuracy of improved cumulative method is higher than the ordinary cumulative method，w hile cumulative method model construction time is not far longer than other.

spindle;thermal error;cumulative method;modeling

TH161;TG506

A

1001－2265(2017)04－0056－04

10.13462/j.cnki.mmtamt.2017.04.014

2016－07－20;

2016－08－15

江苏省前瞻性联合研究项目(BY2016053－04);南通市重大科技创新专项资助(XA2014011)

袁江(1968—)，男，江苏南通人，南通大学副教授，硕士，研究方向为机电系统测控技术，(E－mail)yuanjiang68@126.com。