基于改进蚁群算法的焊接机器人路径规划

金嘉琦，刘畅，徐振伟

基于改进蚁群算法的焊接机器人路径规划

金嘉琦，刘畅，徐振伟

(沈阳工业大学机械工程学院，辽宁沈阳110870)

为了解决目前车身焊接机器人路径规划不合理的情况，分析了焊接机器人运动过程，建立了有效的路径规划数学模型。通过对蚁群算法的研究，将遗传算法的遗传算子理论引入蚁群算法，运用MATLAB编写相应的程序。结果表明，改进蚁群算法能够更好的适用于路径规划，能够规划出一条合理的焊接路径。

焊接机器人;路径规划;改进蚁群算法

0 前言

近年来，随着汽车产业的蓬勃发展，国内绝大多数汽车制造厂商都引进工业机器人来提高生产质量和效率。在汽车的生产中，工业机器人被广泛应用到汽车制造的各个方面，尤其是白车身的焊接方面，机器人以其高质量、高效率和节省劳动力的优点得到各大汽车厂商的青睐。但据统计，每台汽车车身焊点多达4 000～5 000个，分配到每台机器人的焊点也多达几百个，现在人工为主的机器人路径规划缺少理论的认证，存在很大的随机性，没有一个系统的方案，如何高效率的完成焊接，规划出一条节省机器人工位生产时间、提高生产质量的路径成为目前需要解决的问题［1］。

对于焊接机器人在路径规划方面的不合理情况，本文通过对蚁群算法的研究，运用改进的蚁群算法建立路径规划的数学模型，采用MATLAB软件编写相应程序，规划出一条三维空间下的最短路径，最终达到减少机器人工位的生产时间和配合整体工时的目的。

1 路径规划的数学模型

在实际的汽车生产车间，完成一辆白车身的焊接需要多台机器人协同工作，一般情况下为3～4台，一台抓取工件，其它工位负责焊接，以加快生产时间。本文研究的是已经完成焊点分组，负责车门焊接的单台机器人的路径规划。

在焊接机器人工作过程中，机器人手持焊枪从所设定的HOME点出发，从第一个焊点开始，依次焊接，完成一个循环回到HOME点。这与求解TSP问题非常相似，TSP即旅行商问题，旅行者想要在几个城市之间旅行，出发前制定一个系统的旅行方案，从所在城市出发，游玩所有城市后，回到自己所在城市，达到所用路程或时间最短的问题。

机器人在两个焊点之间的运动是以PTP的形式实现，也是速度最快的方式，在焊枪和夹具有干涉的情况下，增加过度点使机器人快速通过障碍。因此，缩短整体工位时间的方式即是减少机器人作业的路程。所以，本文以在焊接机器人在三维焊点之间所走路程最短作为评价准则，其数学模型可表示为:

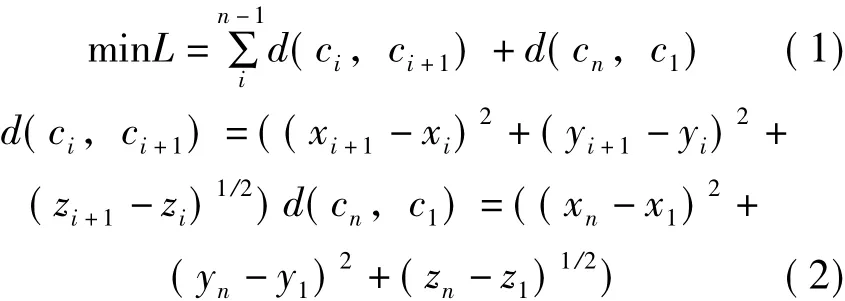
式中，n为车身焊点的个数;d(ci，ci+1)为两个焊点之间的距离。

2 基于改进蚁群算法的路径规划

蚁群算法的构思来自与自然界蚂蚁群体的觅食行为，是一种新兴的启发式仿生进化算法，因其简单、高效率等优点被广泛应用［2］。蚂蚁在寻找食物过程中，会有目的的释放一种信息素来告知后面的蚂蚁距离食物的最短路径，路径越短，走过的蚂蚁越多，信息素浓度越大，因此形成一种正反馈机制。本文采用改进蚁群算法，将遗传算法的遗传算子理论引入蚁群算法，使蚁群算法收敛更快，结果更优，更加适用于路径规划。

2.1 初始信息素设置

在蚁群算法中，初始信息素值设置太小，会导致算法提早进入局部最优，但是，初始值太大，会增加算法的计算量，不易于求解，本文采用如下公式进行设置，

式中，n为焊点的个数;Lnm是由最近的邻域启发产生的一个路径长度。

2.2 蚂蚁在焊点间的转移规则

蚂蚁在运动过程中，由其中一个焊点走到下一个焊点并不是随机的，而是根据各焊点之间路径上的信息素浓度来决定转移方向，本文采用的转移规则为随机比例规则，它给出了位于焊点i的蚂蚁k在选择移动到焊点j的概率。在t时刻，蚂蚁k在焊点i选择焊点j的转移概率为

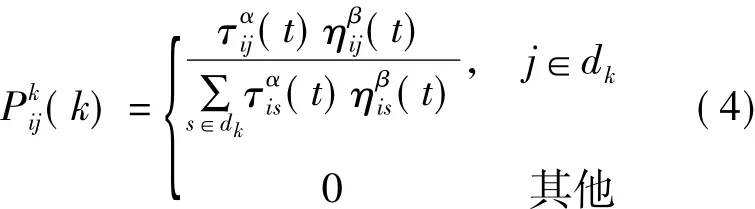
式中，dk={0，1，…，n－1}，表示编号为k的蚂蚁下一步允许选择的焊点;ηij为能见度因数，其值为两焊点之间距离倒数，即ηij=1/dij;α为信息启发因子;β为期望启发因子;α和β分别反映蚂蚁在运动过程中所积累的信息和启发信息在蚂蚁选择路径中的相对重要性。

2.3 信息素更新方案

蚂蚁完成一次循环后，对蚂蚁所走的路径上的信息素浓度进行全局更新，为了避免信息素无限累加，采用蚁周系统进行信息素更新。

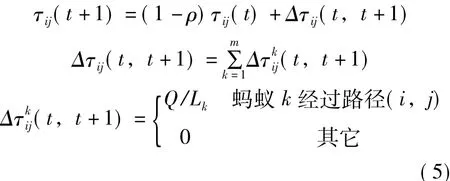
式中，Δτij(t，t+1)表示更新蚂蚁k走过的路径;ρ为信息素挥发系数(0＜ρ＜1);Lk为蚂蚁k在本次循环中所走的路径长度。

2.4 交叉算子

遗传算法的交叉算子可以产生新的个体，维持种群多样性，增强算法的全局搜索能力［3］。当所有的蚂蚁访问完所有的焊点以后，对蚂蚁群体生成的解(蚂蚁走过路径)进行交叉，用以生成更优质的种群。本文采用顺序交叉方法，基于概率Pc先选择两个父代蚂蚁进行双点交叉，再进行维持原有访问顺序的巡回路线修改(与已有编码不重复)，具体如下所示:

父代A:56︱2398︱714

父代B:14︱3269︱758

子代A1:3269︱58714

子代B1:2398︱14675

2.5 变异算子和算子更新

变异算子决定算法的局部搜索能力，与交叉算子配合，使其算法具有良好的搜索性能［3］。对交叉产生的新种群进行变异操作，文章采用插入式变异方法，即随机产生两个变异位置，将第二个变异位插入到第一个变异位前面，如图1所示。变异操作是由变异概率Pm来进行控制。通过对评价函数的比较进行算子更新，如果变异结束后，子代解不如父代，则仍采用父代解。

2.6 算法流程

基于改进蚁群算法的焊接机器人路径规划算法流程如图2所示。

3 运用MATLAB仿真

基于以上算法，运用MATLAB软件编写相应程序，由于蚁群算法是一种概率算法，其需要设置的参数比较多，很难找到一种数学算法计算每个参数的最优值［4］，通过查阅文献和实验可确定各参数初始值设置为:蚂蚁数量m=20，α =1，β=1，ρ=0.05，交叉概率Pc=0.7，变异概率Pm=0.3。输入各车门焊点坐标，通过实验发现，经过100次迭代后可求得最优路径，如图3所示。

从图中看出，输出图形为一条封闭路径，符合机器人工作要求，最优路径结果为:1－5－17－18－16－11－10－6－4－3－2－7－8－9－12－15－14－13－19－22－20－21，最优路径距离为755.107。

4 结论

本文通过对机器人运动状态的分析，建立了求解焊接机器人路径规划的数学模型，采用改进蚁群算法，运用MATLAB软件编写程序，对其数学模型进行优化仿真，结果表明，通过规划后的路径符合机器人的工作要求，对于提高机器人的加工效率，节省加工时间有一定的意义，为焊接机器人路径规划提供了一个新的方法。

［1］彭永健，李小宁．基于蚁群算法的分组焊点焊接路径优化方法研究［J］．机械制造与自动化，2012 (01):6－9．

［2］杨学峰．蚁群算法求解TSP问题的研究［D］．吉林:吉林大学，2010．

［3］雷英杰，张善文．MATLAB遗传算法工具箱及应用［M］．西安:西安电子科技大学出版社，2014．

［4］李士勇．蚁群算法及其应用［M］．哈尔滨:哈尔滨工业大学出版社，2004．

［5］魏安立，胡小建，孙太生．基于遗传算法焊接机器人路径规划研究［J］．现代焊接，2011(08):27 +29．

［6］林巨广，陈甦欣，戴淮初，等．蚁群算法在白车身底板焊接路径规划中的应用［J］．焊接学报，2015．

Path planning of welding robot based on improved ant colony optimization

JIN Jia-qi，LIU Chang，XU Zhen-wei
(School of Mechanical Engineering，Shenyang University of Technology，Shenyang 110870，China)

In order to solve the situation that path planning of welding robot for automobile body is not reasonable，this paper analyzed of the welding robot motion process，established a mathematical model of effective path planning．Through studying ant colony optimization，the genetic operator theory of genetic algorithm was introduced into the ant colony optimization，and the corresponding program was prepared using by MATLAB．The results show that the improved ant colony optimization can better apply to path planning and plan out a reasonable welding path．

welding robot;path planning;improved ant colony optimization

TG457

A

1001－196X(2017)01－0044－03

2016－07－07;

2016－09－29

金嘉琦(1955－)，男，博士，教授，博士生导师，主要研究方向:精密加工与精密测量的理论与技术研究。

刘畅(1992－)，男，硕士研究生，主要研究方向:工业机器人技术。