行星滚柱丝杠副的参数化设计与研究

邢 思，侯红玲，赵永强，孙允璞

(陕西理工大学 机械工程学院，陕西 汉中 723000)

行星滚柱丝杠副的参数化设计与研究

邢 思，侯红玲，赵永强，孙允璞

(陕西理工大学 机械工程学院，陕西 汉中 723000)

提出了行星滚柱丝杠副的参数化设计方案，分析传动原理及运动关系，推导出主要零部件结构参数关系以及计算公式。从载荷、行程、转速、精度等条件入手，分析行星滚柱丝杠副在数控机床中实际应用工况，建立三维数字化模型并进行虚拟装配和干涉检验，验证参数化设计的正确性。

行星滚柱丝杠副； 参数化； 三维建模； 虚拟装配

行星滚柱丝杠副(Planetary Roller Screw Mechanism,PRSM)是一种新型的精密传动机构，用呈行星状均匀分布在丝杠周围的多个螺纹滚柱的行星运动代替滚珠丝杠副中滚珠的循环运动，有众多的螺纹线来支撑负载，通过螺纹传动将电机的旋转运动转化为丝杠或螺母的直线运动[1]。行星滚柱丝杠副的基本原理与滚珠丝杠副、螺母螺杆机构类似，其导程不受滚珠直径限制，可以小于0.5 mm或制造的更小。导程为1～2 mm时，行星滚柱丝杠副的承载能力约为滚珠丝杠副的20倍。当负载要求的情况相同时，行星滚柱丝杠副的体积更小，承载能力更高，同时也具有更长的行程寿命。正是由于它高承载、体积小、高精度、小导程和长寿命的优点，以及在高速、重载、环境恶劣等工作场合的应用也具有显著的优势，受到越来越多的重视，被广泛的应用于飞行器、武器装备等军事领域[2-4]，以及精密机床、光学仪器、石油化工、食品包装、测试仿真等民用领域。

目前,国内外学者主要集中进行了关于行星滚柱丝杠副的发展现状、刚度计算、设计参数匹配、传动精度、运动学分析、啮合状态等方面的研究工作。其中刘更等[5]对行星滚柱丝杠副的原理、关键技术和发展趋势进行了综述；马尚君等[6]结合三角螺纹的变形推导出行星滚柱丝杠副的刚度计算方法，并对行星滚柱丝杠副与滚珠丝杠副的静刚度进行了对比；靳谦忠等[7]通过有限元分析对比了行星滚柱丝杠副与滚珠丝杠副的静刚度；MA Shangjun等[8]通过有限元法对行星滚柱丝杠副中螺纹牙接触角和螺旋升角进行研究，总结出了提高行星滚柱丝杠副传动精度的方法；Lisowski F[9]对行星滚柱丝杠副的位移分析与载荷分布进行研究，分析了各组成部分之间的载荷应力分布情况和丝杠、螺母、滚柱的不同尺寸的螺纹接触刚度；韦振兴[10]利用乘除法和模拟退火算法以行星滚柱丝杠副中齿轮的部分结构参数作为设计变量进行优化分析，缩短了周期，并减少了设计成本；张大伟[11]提出并探讨了一种适于滚柱零件上螺纹和花键同步滚压精确塑性成形新方法，保证其相对位置稳定的同时，避免了行星滚柱丝杠副中相位冲突问题。

综合以上分析可知，对行星滚柱丝杠副的研究涉及到民用领域中较少。本文以某数控机床工作台运动为应用背景，结合实际工况要求和设计计算，对行星滚柱丝杠副进行参数化设计与研究。

1 行星滚柱丝杠副的工作原理

行星滚柱丝杠副的传动原理如图1所示，丝杠1在旋转过程中，丝杠1与滚柱2中间部分的螺纹啮合；滚柱2的螺纹又与螺母3内螺纹啮合，并沿轴线方向移动产生一定的位移，达到了将旋转运动与直线运动相互转换的目的。与此同时，滚柱4两端的螺纹齿与固定在螺母3两端内齿圈5的螺纹齿啮合，既能够保证各滚柱与丝杠1、螺母3间啮合传动的同步性，避免在传动过程中因力矩倾斜导致各滚柱脱离轨道现象的发生[12]，也可以减小滚柱2与丝杠1和螺母3之间的摩擦阻力，增加使用寿命和传动效率。滚柱2端部设计的光轴与行星架H上的孔搭配，确保各滚柱被完全支撑。另外，由于行星滚柱丝杠副没有自锁性，当外界使螺母直线运动时，也可使丝杠转动，即运动时可逆[13]。

1.丝杠，2.滚柱，3.螺母，4.滚柱，5.内齿圈，H.行星架图1 PRSM传动原理图

2 行星滚柱丝杠副的设计

丝杠、滚柱、螺母、内齿圈和行星架等组成一个完整的行星滚柱丝杠副。在设计计算过程中，只有将丝杠和滚柱的螺纹牙，滚柱与螺母之间的螺纹与齿等参数相互配合，才能够使其平稳运动。设计中，首先根据行星滚柱丝杠副的运动条件、啮合原理计算出丝杠、滚柱、螺母的基本尺寸，然后根据相关条件计算出滚柱端部的行星架及内齿圈的基本参数。丝杠和螺母的导程相等，即

Ps=Pn,

(1)

式中：Ps为丝杠导程，Pn为螺母导程。

由行星滚柱丝杠副的工作原理和几何条件可知，为了保证传动比为常数，通常取滚柱、丝杠与螺母三者螺旋方向相同，且具有相同的螺旋升角，滚柱与螺母啮合时确保纯滚动，并且没有相对轴向位移。即

θs=θn=θr,

(2)

式中，θs,θn,θr分别代表丝杠、螺母、滚柱的螺旋升角。

由行星滚柱丝杠副的几何结构可知：

Dn=Ds+2Dr,

(3)

式中：Dn,Ds,Dr分别为螺母、丝杠、滚柱的螺纹中径。

螺母的螺旋升角为：

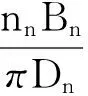
(4)

式中，nn代表螺母的头数，Bn代表螺母的螺距。

滚柱的螺旋升角为：

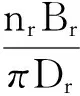
(5)

式中，nr代表滚柱的头数，Br代表滚柱的螺距。

通过式(1)—(5)知：

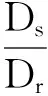
(6)

当丝杠旋转时，滚柱既绕丝杠的轴线公转，又绕自身轴线自转；丝杠旋转一周，滚柱相对丝杠轴向运动，移动一个导程的位移；螺母与丝杠之间无相对移动。因此由图2可知，螺母与丝杠的螺纹头数为[14]：

(7)

式中，nn,ns分别为螺母和丝杠头数。

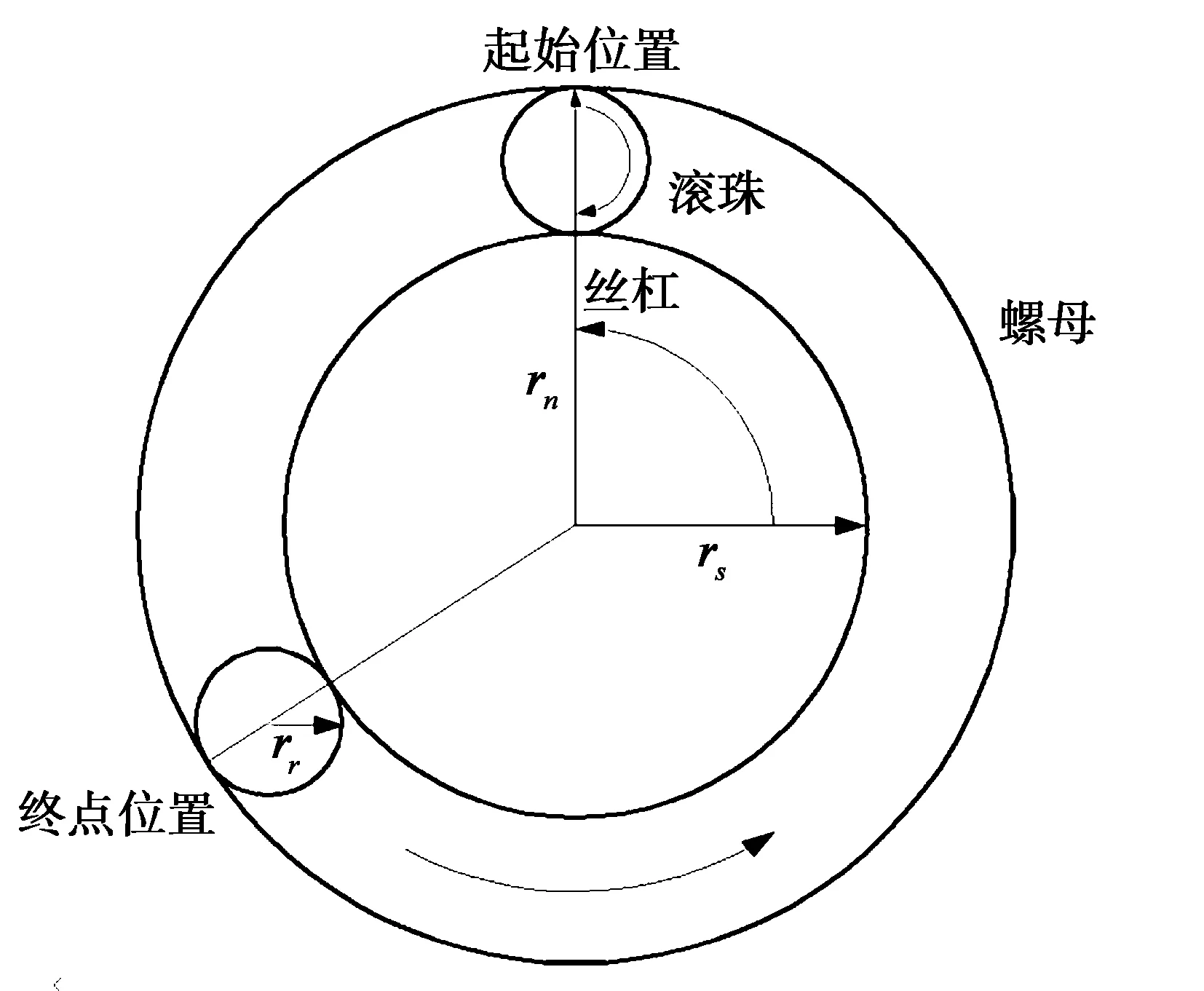
图2 PRSM传动端面图

行星滚柱丝杠副的传动采用行星传动。控制丝杠、螺母和滚柱的接触半径及头数，当丝杠的导程和中径确定时，便可以得到滚柱的头数与中径之间所满足的关系；滚柱端部螺纹齿与安装在两端内齿圈螺纹齿相啮合，保证了滚柱轴线始终与丝杠轴线平行，使滚柱与丝杠和螺母之间保持良好的接触；对螺纹齿的设计不仅要考虑啮合条件，还不能影响丝杠与滚柱的相互运动。如图1所示，假设行星架的转速为γH，由轮系1-2-3之间的传动关系[15]可得：

(8)

由于螺母仅做直线往复运动，所以γ3=0，则

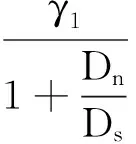
(9)

通过轮系1-2-4-5的传动关系可知：

(10)

同理，γ5=0，故

(11)

令γH=γH*时，得出滚柱端部螺纹齿齿数与内齿圈螺纹齿齿数之间的关系为：

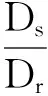
(12)

其中Zn代表内齿圈螺纹齿齿数;Zr滚柱端部螺纹齿齿数。

结合上述关系式可以求得丝杠、滚柱中径比值和滚柱与内齿圈螺纹齿齿数比值之间的关系。在给定工作条件后，就能初步确定行星滚柱丝杠副的结构尺寸，其中包括滚柱中径和头数，滚柱端部螺纹齿齿数和内齿圈螺纹齿齿数，螺母中径等参数的确定。通过模数m的取值来选择，进一步求出Zrm，从而确定Zr的值。

3 应用实例计算

目前的数控机床仍以滚珠丝杠副传动为主，高速运转时，滚动体会产生较大离心力，滚珠受截面积小，轮流受截，会产生循环变应力，进而导致温度急剧升高，使得工作效率和加工精度下降。而行星滚柱丝杠副工作时的额定动载是滚珠丝杠副的2.5倍，根据Hertz pressure(赫兹压力)定律知它所承受静载为滚珠丝杠副的3倍，连续工作寿命是其15倍，最高转速可至5000 r/min，最高线速度可达2 m/s；当负载要求的情况相同时，行星滚柱丝杠副的体积更小。因此，设计一种行星滚柱丝杠副代替机床传统意义上的滚珠丝杠副，不仅能实现大推力、高转速、长寿命，同时还能保证加工精度，减少摩擦损耗，极大的提高机床的工作能力。

假定某数控机床的工作过程分为极限负载、粗加工、精加工、快速进给等阶段，分别通过丝杠的工作时间百分比t、丝杠所承受轴向负载F以及各阶段速度n，要求额定静载荷为70 kN，额定动载荷为60 kN，对行星滚柱丝杠副的工作能力及强度进行校核。

3.1 实际工况分析

在实际工作要求下，通过对平均转速、极限负载、扭矩等计算，评价行星滚柱丝杠副在机床中的工作能力。

3.1.1 平均转速nm

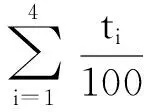
式中，t1，t2，t3，t4分别取5，25，35，5，表示不同工作阶段的时间百分比；n1，n2，n3，n4分别取13，100，70，1300，表示各段转速。

3.1.2 平均加权负载Fm

a) 对于恒定速度而负载在各阶段不断变化F1、F2、F3、F4时，加权平均负载：

式中F1，F2，F3，F4分别取9000，4000，3500，900，表示各段实际负载。

b) 对于速度变化同时负载也不断变化时，加权平均负载：

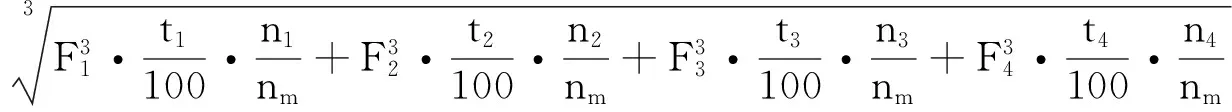
因此，在负载线性变化时的平均加权负载Fm为

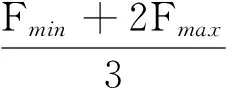
3.1.3 驱动扭矩Mm

丝杠运转时，F1为极限负载下的轴向力，按实际峰值载荷F1=9000 N计算，提升负载扭矩就是：

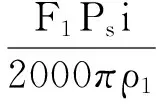
式中，Ps表示丝杠导程，取10 mm；i表示减速比，取1；ρ1表示上升传动效率，取0.87。

下降负载扭矩：

式中,ρ2表示下降传动效率，取0.83。

假设丝杠支撑端的轴承的摩擦扭矩Mz=0.3 N·m，则丝杠在恒速条件下，达到峰值时的驱动扭矩为

Mm=MF1+MF2+Mz=28.65 N·m。

3.2 强度设计计算

行星滚柱丝杠副的强度计算和普通机械零件的强度计算方法类似，即在不同破坏形式下，分别推导出计算公式，同时考虑参数选取是否合理。在传动过程中，零件失效的主要形式是螺纹磨损、丝杠受压失稳、丝杠断裂以及螺纹牙折断或剪切等；传动间隙过大或传动刚度不足时，也会极大影响行星滚柱丝杠副的传动性能。一般情况下，可以先根据耐磨性计算出丝杠的直径，再根据可能发生的失效形式对其进行校核[16]。上述对行星滚柱丝杠副工作能力的计算可知，丝杠受轴向负载的同时，丝杠螺纹与滚柱螺纹之间相互挤压，通过强度设计计算公式，进行如下校核：

3.2.1 丝杠强度校核

丝杠在承受轴向负载时产生轴向拉(压)应力，同时承受电机驱动扭转力矩，产生截面扭切应力。根据丝杠在极限负载时所受到的轴向力F=9000 N，恒速峰值时的驱动扭矩Mm=28.65 N·m，计算丝杠当量应力。

根据第四强度理论得出危险截面的当量应力δε应为：

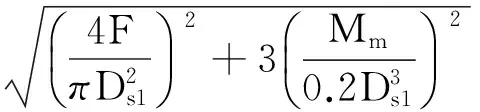
式中Ds1指丝杠小径；[δρ]=δ*/φ表示材料的许用拉应力，其中δ*指材料屈服强度，φ是安全系数，常取3～5。

3.2.2 螺纹抗剪强度校核

在螺纹啮合时，螺纹牙根部受到的剪应力最大。同时，许用剪应力还必须大于螺纹牙受到的剪应力，根据丝杠在极限负载时所受轴向力来计算螺纹所受剪应力，即

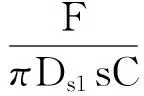
式中s=0.74Bs为螺纹牙根部宽度，其中Bs为丝杠螺距，取2 mm；C为螺纹旋合圈数，取30；[τρ]为材料许用剪应力。丝杠外螺纹所受剪应力远小于材料的许用剪应力，因此抗剪强度满足条件。

3.2.3 丝杠稳定性校核

丝杠是长度较大的杆件，它的支撑长度、抗弯刚度等，均与临界载荷有密切联系。当丝杠所受的轴向力比临界载荷大时，会发生扭转变形并失去稳定性，一旦稳定性丧失可能导致机器损坏。若丝杠直径越小，支撑长度越长，产生扭转变形的可能性就越大。因此，进行相关强度的校核之后，还必须计算稳定性，以确保传动正常。假定丝杠一端固定，一端自由，此时支撑系数k=2.5×104，即使在极限负载下，丝杠也不会失稳，则丝杠所受的临界稳定载荷FL为

式中E表示材料的弹性模量；β指长度因数；l表示丝杠的最大工作行程，取700 mm；k=π3E/(64β2)为支撑系数，满足稳定性条件。

3.2.4 丝杠耐磨性校核

如果F按照机床工作中的最大负载计算，即F=9000 N，丝杠中径尺寸Ds范围如下：

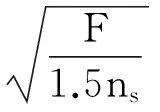
式中ns为丝杠头数。

综上校核计算，在满足该数控机床的工作要求的情况下，本文拟取丝杠中径为30 mm。

3.3 参数化设计计算结果

实际应用中，行星滚柱丝杠副的选定将影响整个设备的工作效能。在进行核心参数的确定时，应综合考虑所设计设备的负载、精度、速度、行程等要素，以及该设备所要求的各种功能因素，经校验全部满足条件后，选定最适合的行星滚柱丝杠副，实现整个设备的最佳工作效能，发挥其最大价值。下面将以上述选取的数控机床工作要求为前提，以在该条件下行星滚柱丝杠副的工作能力及强度校核计算分析为原则，对满足要求的丝杠中径进行确定，并以螺纹、齿等设计计算为依据，对行星滚柱丝杠副的主要部件进行结构参数化设计，具体结构见图3。

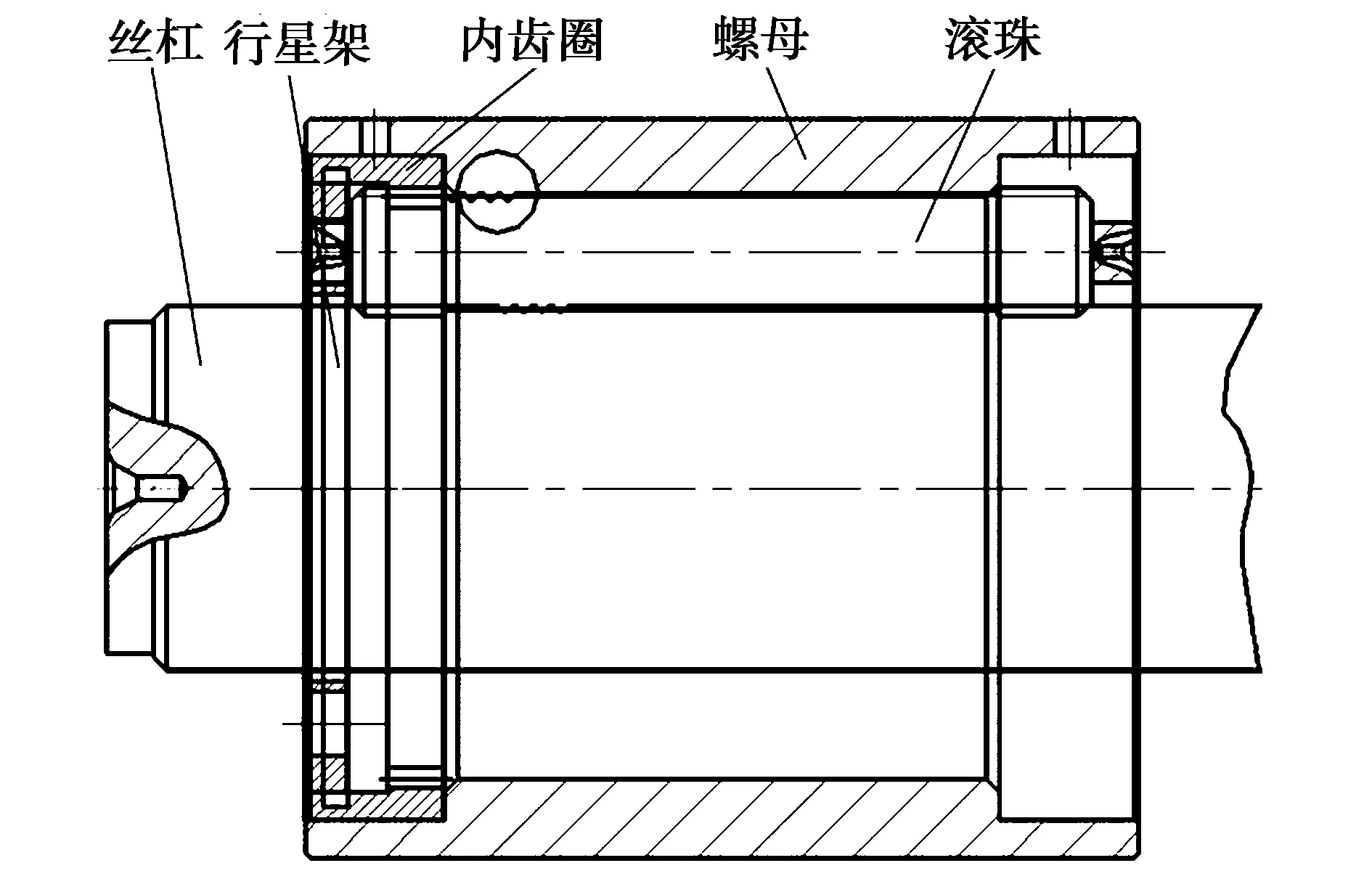
图3 PRSM结构示意图

3.3.1 丝杠的参数设计计算

根据以上公式推导计算，取丝杠中径为Ds=30 mm，导程Ps=10 mm，头数5头，螺距Bs=2 mm，接触角η=45°，其中，丝杠的螺纹牙型为三角形，牙型角为90°，设计旋向为右旋；ac为牙顶间隙，取0.15。

基本牙型高：H1s=0.5Bs=1 mm; 外螺纹牙高：H2s=H1s+ac=1.15 mm; 牙顶高：Z=0.25Bs=0.5 mm; 丝杠大径：Ds3=Ds+2Z=31 mm; 丝杠小径：Ds1=Ds3-2H2s=28.7 mm。

3.3.2 滚柱的参数设计计算

滚柱为单螺纹，取滚柱螺距为Br=2 mm，设计旋向为右旋，由2节中公式可知丝杠和滚柱的中径比Ds/Dr=3。滚柱中径：Dr=1/3Ds=10 mm; 滚柱大径：Dr3=Dr+2Z=11 mm; 滚柱小径：Dr1=Dr3-2H2s=8.7 mm。

3.3.3 内齿圈的参数设计计算

根据装配及设计要求，取内齿圈的螺纹齿宽bn=br=10 mm，内齿圈厚度为滚柱端部螺纹齿的齿宽和行星架厚度之和，即为15 mm。

3.3.4 螺母的参数设计计算

由式(3)可知，螺母中径Dn=Ds+2Dr=50 mm;螺母大径Dn3=Dn+2Z=51 mm;螺母小径Dn1=Dn3-2H2s=48.7 mm。

参照以上结构参数的设计标准，对行星架、挡圈等部件尺寸进行设计。通过整理计算得出行星滚柱丝杠副，滚柱与内齿圈的螺纹齿基本结构参数分别见表1和表2。

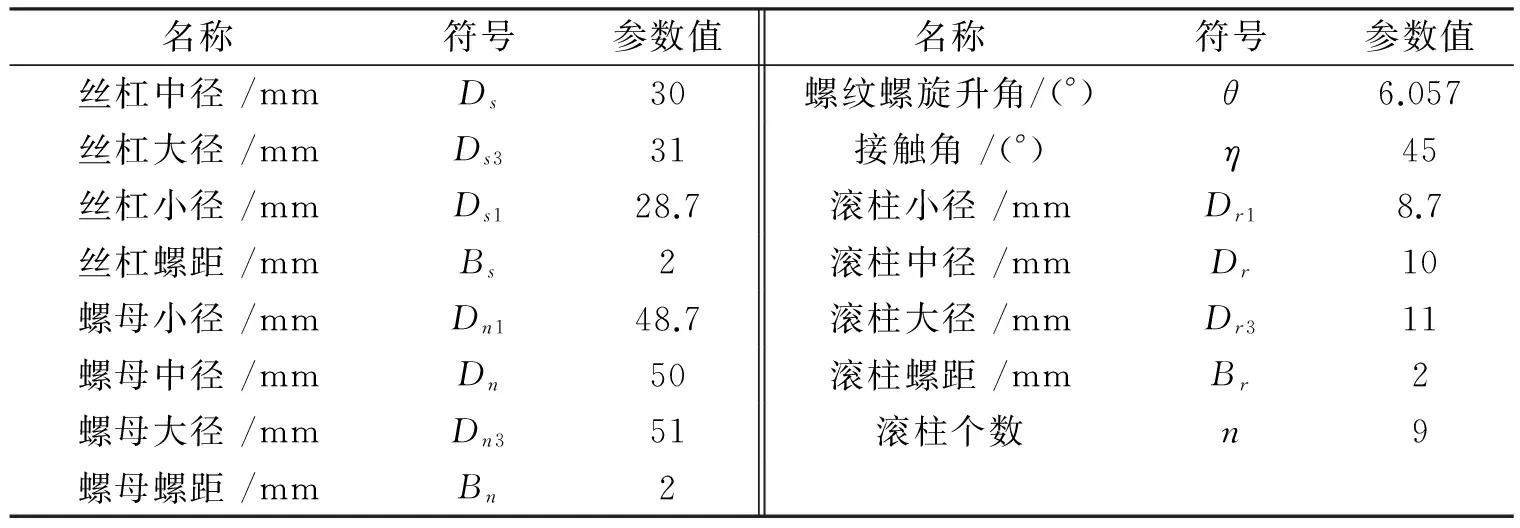
表1 PRSM基本结构参数

表2 螺纹齿基本结构参数

4 行星滚柱丝杠副的建模与装配

根据上述的计算结果，为了验证计算的正确性，现运用ProE软件建立该机构的三维数字化模型，并进行虚拟装配和干涉检验。

4.1 主要零部件的建模

建模时，丝杠的设计采用5头螺纹，以丝杠的导程作为螺距进行螺旋扫描，绘制单头螺纹，再将扫描后的单头螺纹通过丝杠轴线轴向阵列，阵列个数为丝杠头数，得到多头螺纹丝杠；滚柱螺纹与丝杠螺纹和螺母螺纹相互旋合，在拉伸后的滚柱端面绘制齿廓线，输入函数绘出螺纹齿渐开线，通过去除材料得到滚柱端部螺纹齿。其中从滚柱端部进行螺旋线扫描绘制螺纹，扫描去除轮廓绘制基准面与螺旋线基准面垂直，去除的牙底宽度应尽量保持一致。丝杠外螺纹与螺母内螺纹具有相同的头数和牙型，牙型角为90°。螺母螺纹设计与丝杠相同。行星滚柱丝杠副的主要零部件模型如图4所示。

图4 行星滚柱丝杠副的主要模型图

4.2 虚拟装配

装配时，首先将两个内齿圈对称安装在螺母的内部，再将行星架和挡圈安装于螺母一端；其次，安装滚柱到螺母内部，并将端部的光轴与行星架上的孔搭配，采取阵列的方式在圆周方向上对滚柱进行装配。滚柱与螺母装配完成后，在螺母另一端安装对应的行星架和挡圈，确保滚柱被完全支撑。最后，将丝杠旋入，完成装配。装配过程中，可以通过调整螺纹牙的厚度来消除螺纹啮合时产生的干涉问题。为了保证丝杠与滚柱的正确啮合，通常将丝杠与起始位置处的滚柱装配要正确配合。为了保证螺纹牙与齿轮的正确啮合，满足滚柱螺纹大径与其端部螺纹齿齿顶圆直径要相等，同时满足起始位置处的滚柱与螺母齿轮和螺纹牙的正确啮合。行星滚柱丝杠副装配图如图5所示。结合上述结构参数化设计计算，依托国内某企业对其进行加工制造，样件如图6所示。

图5 PRSM完整装配图 图6 PRSM样件

4.3 材料和主要加工工艺

在行星滚柱丝杠副的结构设计中，通常将5～12根小滚柱均匀环绕在丝杠周围，使其受力特征相同。为了使行星滚柱丝杠副的工作性能和运动精度达到该应用场合的传动要求，提高承载能力并延长寿命。丝杠、螺母和滚柱的材料选用高碳铬轴承钢GCr15，该材料具有良好的耐磨性，高的接触疲劳性能和淬透性，热处理后可获得高且均匀的硬度，接触疲劳强度高，有良好的尺寸稳定性和抗蚀性，也可承受大负荷；内齿圈与行星架则选用42CrMo钢，它的强度、淬透性高，韧性好，高温时蠕变和持久强度高，用于制造强度更高、调质截面更大的锻件，如增压器传动齿轮、受载荷极大的连杆、弹簧夹等。因此，材料的选择应由产品的具体工作场合确定。

为保证装配阶段滚柱螺纹与螺母螺纹、滚柱端部螺纹齿与内齿圈螺纹齿同时啮合，加工时主要考虑螺纹与齿的加工。对于滚柱而言，通常先加工出滚柱的螺纹，确保每个滚柱切齿位置在螺纹的同一起点处；再加工两端螺纹齿，一般采用插齿法加工螺纹齿，来减少局部螺纹的损伤，避免降低承载力[5]。

5 结束语

本文分析了行星滚柱丝杠副的工作原理和运动关系，推导出关键零部件的尺寸关系以及参数计算公式，并通过构建螺纹的设计方法对主要部件进行三维建模和虚拟装配。此研究不仅为行星滚柱丝杠副的各部件加工提供了指导，还为传动装置的应用提供了依据；设计过程简便，结果可靠，能够满足实际工况设计要求。随后将通过跑合加载试验，通过模拟实际工作过程，对其进行性能试验研究，进一步提高机床的承载能力和传动效率，降低摩擦，扩大该传动装置在工程中的推广应用。

[1] 董永,刘更,马尚君，等.行星滚柱丝杠副滚柱的设计方法与虚拟装配[J].机械设计,2013,30(8):53-57.

[2] ROSERO J A,ORTEGA J A,ALDABAS E,et al. Moving towards a more electric aircraft[J].IEEE Aerospace and Electronic Systems Magazine,2007,22(3):3-9.

[4] ABDELHAFEZ A A,FORSYTHA J. A Review of More-Electric Aircraft[C].13thInternational Conference on Aerospace Sciences & Aviation Technology,ASAT-13,2009:1-13.

[5] 刘更,马尚君,佟瑞庭,等.行星滚柱丝杠副的新发展及关键技术研究[J].机械传动,2012,36(5):103-108.

[6] 马尚君,刘更,佟瑞庭,等.行星滚柱丝杠副轴向弹性变形的有限元分析[J].机械传动,2012,36(7):78-81,98.

[7] 靳谦忠,杨家军,孙健利.滚珠丝杠副和行星式滚柱丝杠副静刚度的比较研究[J].机械科学与技术,1999,18(2):230-232.

[8] MA Shang-jun,LIU Geng,ZHOU Jian-xing. Optimal Design and Contact Analysis for Planetary Roller Screw[J].Applied Mechanics and Materials,2011，86:361-364.

[9] LISOWSKI F. The Analysis of Displacements and the Load Distribution Between Elements in a Planetary Roller Scr-ew[J].Applied Mechanics and Materials,2014，680：326-329.

[10] 韦振兴.行星滚柱丝杠副刚度及效率的分析与研究[D].武汉：华中科技大学,2011.

[11] 张大伟,赵升吨.行星滚柱丝杠滚柱塑性成形的探讨[J].中国机械工程,2015,26(3):385-388.

[12] 赵英,倪洁.滚柱丝杠副的啮合计算[J].机械设计,2003,20(3):34-36.

[13] 陈芳.两级行星滚柱丝杠传动设计与精确度研究[D].南京：南京理工大学,2009.

[14] 靳谦忠,杨家军,孙健利.行星式滚柱丝杠副的运动特性及参数选择[J].制造技术与机床,1998(5):13-15.

[15] 饶振刚.行星传动机构设计[M].2版.北京:国防工业出版社,2014.

[16] 徐灏.机械设计手册：第3卷[M].2版.北京:机械工业出版社,2006:378-380.

[责任编辑：张存凤]

Parametric design and research of planetary roller screw mechanism

XING Si,HOU Hong-ling,ZHAO Yong-qiang,SUN Yun-pu

(School of Mechanical Engineering,Shaanxi University of Technology,Hanzhong 723000,China)

The paper has put forward the parametric design scheme,analyzed the transmission principle and kinematic relation of the planetary roller screw mechanism,and derived the structure parameters relationship and the computational formula of the main parts. Starting from the load,stroke,speed,accuracy and other conditions,the paper has analyzed the actural application performance of planetary roller screw mechanism,established the 3D digital model to realize virtual assembly and interference test. And verified the correctness of parametric design.

planetary roller screw mechanism; parameterization; 3D modeling; virtual assembly

2096-3998(2017)03-0010-08

2016-12-21

2017-04-10

陕西省教育厅专项科研计划项目(16JK1166)；陕西省科技统筹创新工程计划重点项目(2014SZS16-K03)；陕西理工大学研究生创新基金资助项目(SLGYCX1726)

邢思(1991—)，女，陕西省蒲城县人，陕西理工大学硕士研究生，主要研究方向为机械传动与优化设计技术；[通信作者]侯红玲(1976—)，女，陕西省扶风县人，陕西理工大学副教授，硕士生导师，硕士，主要研究方向为精密加工技术及设备、数控技术及应用。

TH132.1

A