各向异性空间中的格林函数

李 瑾，冯晓毅，王明军

(1.陕西学前师范学院 计算机与电子信息系，陕西 西安 710100；2.西北工业大学 电子信息学院，陕西 西安 710072；3.西安理工大学 自动化与信息工程学院，陕西 西安 710048)

各向异性空间中的格林函数

李 瑾1,2，冯晓毅2，王明军3

(1.陕西学前师范学院 计算机与电子信息系，陕西 西安 710100；2.西北工业大学 电子信息学院，陕西 西安 710072；3.西安理工大学 自动化与信息工程学院，陕西 西安 710048)

自由空间和各向同性介质空间中的格林函数被广泛应用于求解非齐次标量势的分布问题；各向异性介质空间的格林函数对于研究各向异性介质中电势的分布具有重要的理论意义和应用价值。基于各向同性空间的格林函数和电磁场的多尺度理论，将各向异性介质空间进行各向同性化处理，得到了各向异性介质中的格林函数。通过所得结果，研究了点电荷在各向异性介质中所激发的电势；验证了所得结果的正确性，所得结果为研究各向异性介质中的相关静电场边值问题做了有益的探索。

格林函数； 多尺度理论； 各向同性化

在各向同性介质空间或自由空间，国内外许多学者[1-3]系统地研究了格林函数，并将所得结果成功地用于解决有关的实际问题，如二阶椭圆形偏微分方程[4]、气压变化对重力场观测影响[5]以及多终端量子链状体系电子输运性质的研究等[6]，这些研究及应用表明，各向同性介质空间中的格林函数已比较完善。由于格林函数的获得与各向同性介质空间的泊松方程有关，因此，现有文献已获得的格林函数难以适用于各向异性介质空间；各向异性介质空间的格林函数研究及其应用等未见报道。在电各向异性空间中，电位矢量与电场强度的关系与方向有关，呈现在泊松方程中，电势空间二阶导数前面的系数不同[7]。为了获得各向异性介质空间的格林函数，本文基于各向同性空间的格林函数和电磁场的多尺度理论[8]，将各向异性介质空间进行同性化处理，得到了各向异性介质中的格林函数，利用格林积分公式，获得了点电荷在各向异性介质中所激发的电势。

1 各向同性均匀空间中的格林函数

在各向同性均匀空间(或自由空间)中，标量电位φ满足泊松方程

2φ=-，

(1)

格林函数满足微分方程

2G=-，

(2)

(3)

以z=0为导体分界面，上半均匀空间的格林函数为

(4)

其中ε0为上半均匀空间的介电常数，格林函数的本质是单位点电荷在不同的各向同性均匀介质组合情况下产生的电势。

2 各向异性介质中的格林函数及应用

为了简单起见，可设介电常数张量为[9]

显然，εx,εy,εz构成了介质的相对介电常数张量，是一个无量纲的物理量。由于电场强度和点位移矢量的关系为

考虑到

(5)

直接求解上式比较困难，为此引入多尺度坐标系∑，其中的坐标用ξ1,ξ2,ξ3表示，且

(6)

则式(5)变为

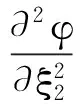
(7)

式(7)利用了电势和电荷为尺度不变量的特性，从而表明：引入多尺度因子后，电荷激发的电势就像自由空间电荷激发的电势，只是自由空间的介电常数变为ε0ξ=abcε0。由式(1)、(2)可以看出，各向同性空间电势满足的方程与格林函数满足的方程有着确定的对应关系，在多尺度坐标系中，式(7)是电势所满足的微分方程；将(7)与(2)比较可得多尺度坐标系∑中的格林函数，用符号G(ξ,ξ′)表示，其中ξ′代表点电荷所在点，ξ代表观察点。格林函数满足的微分方程为

2G(ξ,ξ′)=-，

(8)

从现有文献和(7)可知，在ξ′点上的单位点电荷在无界空间中激发的电势在尺度坐标系为

其中Rξ为点电荷到观察点的距离。因此无界空间的格林函数为

(9)

将(9)从多尺度坐标系∑变换到笛卡尔坐标系，可得

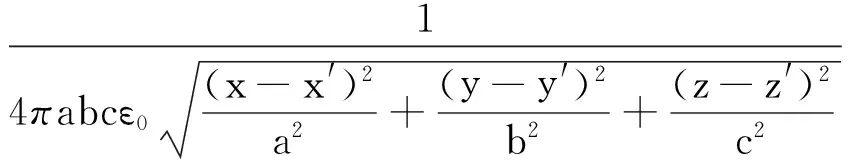
(10)

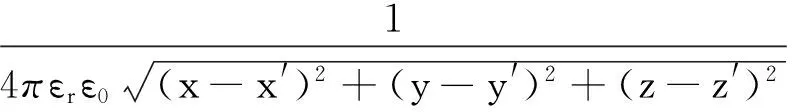
上式为各向同性介质空间的第一类格林函数，与现有文献完全一致，表明了(10)的正确性。对于第一类边界条件，格林函数在边界面S′上为零；由格林公式可得电荷分布为ρ的带电体激发的电势为

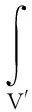
当闭合曲面为无限大时，电势按r-1减小，格林函数的导数按r-2减小，他们的乘积按r-3减小，但是面积按r2增大，三者的乘积按r-1减小，故闭合曲面为无限大时上式第二项为零，将(10)代入可得各向异性介质中任意带电体的电势为

(11)

当r′≪r，上式中的分母可近似为常量，即

由此易得一个点电荷q激发的电势为

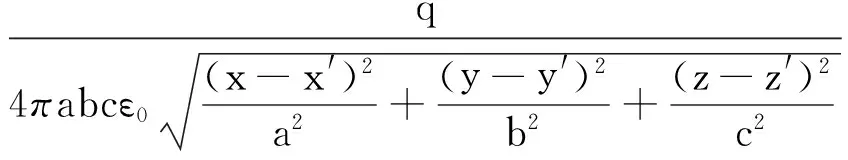
(12)

3 小结与展望

本文研究了各向异性无损耗介质空间中的格林函数，应用其成功地获得了点电荷所激发的电势；对于介电常数张量为对称张量的各向异性介质，可以通过坐标轴的旋转，将其变为对角张量，因此本文结果稍加修改，即可应用于介电常数张量为对称张量的各向异性介质。对于有损耗的各向异性介质，介电常数张量的元素一般为复数；如何探索出新的创新性的思路，研究有耗各向异性介质中的格林函数，这也是下一步将要开展的研究课题。

[1] 王家礼,朱满座,路宏敏.电磁场与电磁波[M].西安:西安电子科技大学出版社,2000:35-38.

[2] 王一平,陈达章,刘鹏程.工程电动力学[M].西安:西安电子科技大学出版社,1985:78-83.

[3] 郭硕鸿.电动力学[M].北京:高等教育出版社,2011:56-63.

[4] 张宏浩.泊松方程格林函数的傅里叶积分求解[J].大学物理,2015,34(12):14-17.

[5] 孙和平.大气重力格林函数[J].科学通报,1997,42(15):1640-1646.

[6] 戴振宏,倪军.基于格林函数的多终端量子链状体系电子输运性质的研究[J].物理学报,2005,54(7):3342-3348.

[7] 李应乐,李瑾,王明军,等.基于波束级数展开的粒子椭圆高斯波束散射特性[J].中国科学G,2014,44(5):465-471.

[8] 李应乐,黄际英.电磁场的多尺度变换理论及其应用[M].西安:西安电子科技大学出版社,2006:32-36.

[9] LI Y L,WANG M J.Electric fields inside and outside an anisotropic dielectric sphere[J].Chinese Physics B,2009,18(6):2420-2428.

[责任编辑：魏 强]

Green function in space of anisotropic medium

LI Jin1,2,FENG Xiao-yi2,WANG Ming-jun3

(1.Department of Computer and Electronic Information,Shaanxi Xueqian Normal University,Xi’an 710100,China;2.College of Electronic Information,Northwestern Polytechnical University,Xi’an 710072,China;3.School of Automation and Information Engineering,Xi’an University of Technology,Xi’an 710048,China)

The Green function of free space and the isotropic media space is widely used to solve the problems of nonhomogeneous scalar potential distribution. The Green function of anisotropic space has important theoretical significance and application value in solving the electric potential distribution of anisotropic media. Based on the Green function of the isotropic space and the scales theory,the anisotropic medium is changed as an isotropic material in physics. The Green function of anisotropic space is presented. The electric potential induced by the electric charge in the anisotropic medium is obtained by using the Green function. The correctness of the obtained results is tested. This article has conducted useful researches for the static boundary value problems of anisotropic medium.

Green function; scales theory; isotropization

2096-3998(2017)03-0085-04

2017-02-17

2017-03-09

国家自然科学基金资助项目(60971079，61102018，61271110)；陕西省教育厅自然科学基金资助项目(16JK1185)；陕西学前师范学院专项科研基金资助项目(2015ZDKJ009)

李瑾(1986—)，女，陕西省西安市人，陕西学前师范学院讲师，硕士，西北工业大学博士研究生，主要研究方向为电磁波传播与散射；冯晓毅(1969—)，女，陕西省西安市人，西北工业大学教授，博士生导师，博士，主要研究方向为计算机视觉、雷达成像与目标识别；王明军(1978—)，男，陕西省汉中市人，西安理工大学教授，博士，主要研究方向为目标粗糙面散射。

O436.1; O241.82

A