林分径级分布预测模型参数的贝叶斯法估计1)——以金沟岭林场样地数据为例

于汝川 张青 岳朝方 亢新刚

(北京林业大学，北京，100083) (德国巴登—符腾堡州林业科学研究院) (北京林业大学)



林分径级分布预测模型参数的贝叶斯法估计1)
——以金沟岭林场样地数据为例

于汝川 张青 岳朝方 亢新刚

(北京林业大学，北京，100083) (德国巴登—符腾堡州林业科学研究院) (北京林业大学)

以吉林省金沟岭林场云冷杉针阔混交异龄林26块检查法样地的5次观测数据为基础，建立转移矩阵模型对一定周期的林分径级分布进行预测。分别利用经典统计学方法和贝叶斯方法对转移矩阵模型的参数进行估计，建立了固定参数的矩阵模型和贝叶斯矩阵模型，并对两种模型的预测效果进行对比。结果显示，固定参数的转移矩阵模型对林分径级分布的预测值比实际值偏高，贝叶斯模型的预测结果更接近林分的实际径级分布，证明了贝叶斯参数估计方法比固定参数平均的方法所建模型具有更高的预测精度。

转移矩阵模型；林分径级分布；贝叶斯统计；MCMC方法；Gibbs抽样算法

贝叶斯法是基于贝叶斯定理而发展起来用于系统地阐述和解决统计问题的方法[1]。与经典统计学相比，贝叶斯统计具有综合利用先验信息和样本信息、把样本和参数都看作随机变量、对参数或模型的构造要求少、不要求样本服从正态分布等优点。许多学者对贝叶斯统计在林业上的应用进行了探索和研究，早在20世纪80年代，贾乃光[2]就曾指出，贝叶斯统计学在林业中的应用前景是完全可以肯定的。张雄清等[1，3]利用贝叶斯方法估计杉木人工林林分断面积生长模型及树高生长模型的参数，取得了较好的建模效果，姚丹丹等[4]利用贝叶斯方法研究长白山落叶松林分优势高生长模型，证明了贝叶斯方法具有一定的优越性。在林业研究中，每隔一定年限对样地进行的重复调查数据使得林业研究往往具有充足的历史资料，这些资料所包含的信息是进行统计预测不可缺少的一个因素。这些信息在贝叶斯统计中可作为先验信息得到充分的利用，每一次调查数据的分析结果都是下一次调查分析最合理的先验信息。因此，贝叶斯模型在林业数据的建模研究中具有一定的优势。

径级分布模型是研究林分结构较常用一种模型。将林分按照树木的胸径大小统计各径级的立木数量即可得到径级分布模型。该模型有效简化了复杂的林分结构，为许多林业经营问题的研究提供了便利和基础。一些关于天然异龄林混交林经营的模型(如均衡曲线模型)都是以林分的径级分布模型为基础发展而来的[5]。

转移概率矩阵模型[6-8]是用来预测林分径级分布的一种模型。该模型可对被径级分布模型简化后的林分内部结构进行建模研究，能反映出林分径级之间的发展变化关系。转移矩阵模型中有许多参数(即转移概率)需要进行准确的估计，许多学者给出了不同的估计方法，Solomon et al.[9]提出两级预测模型，把矩阵模型的参数作为林分指标的函数用线性回归进行估测。由于林分参数之间并非线性关系，Klädtke和Yue[10-11]利用非线性实时参数模型模拟矩阵参数与林分密度和采伐强度的动态关系。以上方法都是基于经典统计学方法进行的参数估计，笔者采用了贝叶斯方法对转移矩阵模型的参数进行估计研究，并与一些经典统计方法进行对比，以检验贝叶斯方法在林业模型研究中的优点和不足。

1 研究区概况

研究地区位于吉林省金沟岭林场(43°22′N，130°10′E)。地貌属低山丘陵，海拔300～1 200 m，坡度5°～25°。该地区属季风型气候，全年平均气温3.9 ℃，年降水量600～700 mm，年生长期为120 d。研究区林分主要为天然针阔混交林，植被属长白山植物区系，立地条件较好，植物种类繁多。主要树种有云杉(Piceakoraiensis)、冷杉(Abiesholophylla)和红松(Pinuskoraiensis)，其他树种有：色木(Acermono)、水曲柳(Fraxinusmandschurica)、胡桃楸(Juglansmandshurica)、黄波椤(Phellodendronamurense)、白桦(Betulaplatyphylla)等[12-13]。

本研究采用金沟岭林场第一大区第5小区的检查法数据，共有26块样地，每块样地面积0.04 km2，总面积1.04 km2。如表1所示，样本包含了从1993—2013年间共5次的调查观测数据，相邻两次调查的时间间隔为5 a。因各年的调查月份不同，考虑到研究区生长季的问题，本研究按照Huang等[14-15]提出的北方森林生长季法，将各调查年份的数据统一转换到当年5月份。

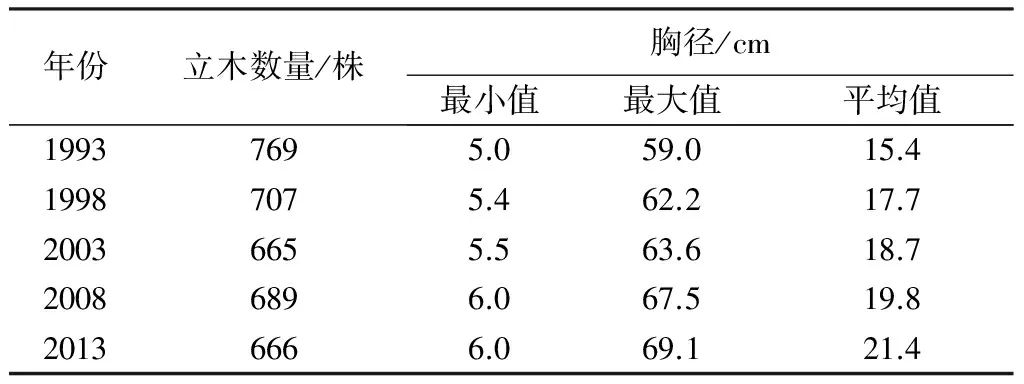
表1 立木数量及胸径统计

2 研究方法

2.1 模型设定

设定林分的起始径级为4 cm，级差为4 cm，径级数设定k=15，建立径级分布模型。图1展示了该研究区每公顷样地各年份的林分径级分布。可以看出，该林分各年的径级分布大致服从反“J”型的指数分布。

2.2 转移概率矩阵模型

对林分径级分布的预测可以采用转移概率矩阵模型，该模型描述如下：

设ω表示预测周期，k为林分的径级数，Nt表示林分t时刻的观测径级分布，A表示转移概率矩阵，M表示枯损率，I表示进界率，则间隔ω时间预测的径阶分布Nt+ω为

Nt+ω=ANt-MNt+INt。

(1)

用矩阵表示为

(2)

式中：ak为由径级k到k+1的进阶生长率；bk为径级k中留余立木数量的比例；ck为由径级k到k+2的进阶生长率；mk为径级k的立木枯损率；ik为径级k的进界率；nk,t为t时刻径级k的立木数量。该矩阵模型的参数可根据实际样本数据进行估计，参数一旦确定，其在时间上就保持不变。

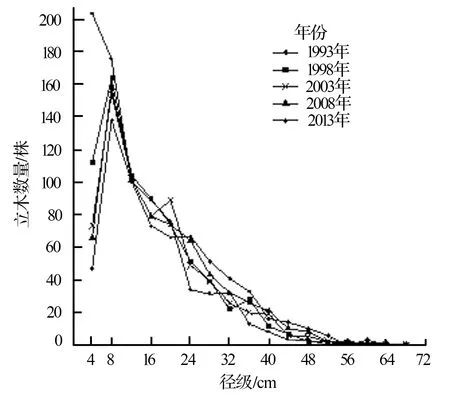
图1 不同年份的林分径级分布

2.3 模型参数的估计方法

2.3.1 固定参数模型

固定参数模型的参数可直接利用林分在一个预测周期前后的两次观测数据直接求解和估计：

(3)

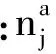
2.3.2 贝叶斯模型

贝叶斯统计思想认为模型的所有参数及预测值均可看作服从某种分布的随机变量。设θ为模型的参数向量，则模型预测值y的密度函数可记为f(y|θ)，其中f为模型参数与预测值的连接函数。给定参数的先验密度函数为g(θ)，若观测到某个预测值样本后，则参数θ的后验密度g(θ|样本)∝g(θ)f(样本|θ)，贝叶斯模型参数的估计可根据其后验密度函数得到。

对于转移概率矩阵模型，根据贝叶斯模型参数估计方法，可建立贝叶斯模型如下：

在一个预测周期ω过后，林分各径级的立木数量

(4)

其中，

μ1=n1,t(b1-m1+i1)；μ2=n2,t(b2-m2+i2)+n1,ta1；

μp=np,t(bp-mp+ip)+np-2,tcp-2+np-1,tap-1,

p=3、…、k-2；

μk-1=nk-3,tck-3+nk-2,tak-2,μk=nk-2,tck-2。

(5)

用向量和矩阵表示为：

(μ1,μ2,…,μk)=μ=ANt-MNt+INt。

(6)

在转移概率矩阵A中，设定参数服从正态分布

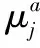
(7)

在向量M和I中，设定参数服从正态分布

(8)

由于模型参数均为概率值，因此将其正态分布均值的先验密度设定为0到1上的均匀分布，即

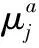
(9)

上述所有正态分布的随机方差均从反伽马分布中进行抽样，即

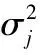
(10)

2.3.3 贝叶斯模型求解

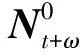
2.4 模型评价

采用均方误差MSE、均方根误差RMSE以及平均绝对百分误差MAPE来衡量模型的预测效果，其计算公式如下：

(11)

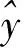
3 结果与分析

由于原始样本共包含5次观测年份的数据，建模过程中利用前4次(1993年、1998年、2003年和2008年)观测数据作为训练样本来估计模型的参数，利用第5次(2013年)观测数据作为测试样本来测试和评价所建立模型的预测精度和效果。模型的预测周期ω设定为5 a。

3.1 固定参数模型的参数估计

利用R语言编程计算固定参数模型的参数，训练样本中的相邻两次测量可估计出一组参数值，4次测量共可计算出3组参数估计值。为充分利用训练样本中所包含的信息，取3组参数估计值的平均值作为最终的固定参数模型的参数估计，结果如表2所示。

3.2 贝叶斯模型的参数估计

贝叶斯模型的参数是根据某一观测值出现后的后验概率密度进行估计的，因此该模型的参数估计会随着每次新观测数据的出现而进行更新调整，这样调整后的后验密度信息中不但包含先验信息，而且包含了样本中的全部信息，因此模型参数估计的精度会随着样本信息的不断更新而逐渐提高。

首先设定模型参数的先验信息，即各参数服从正态分布，且分布的均值为0到1上均匀分布的随机变量；然后结合1993年和1998年的样本信息求得参数的后验密度，该后验密度中包含了先验信息和样本信息；然后将得到的后验密度结果作为下一次模型更新的先验信息，再结合下一周期(1998和2003年)的样本信息求得更新后的后验密度，以此类推重复上述过程，不断加入新的样本信息进行模型参数的后验样本更新，直到将训练样本中4次测量的样本信息全部包含到后验密度中，最后利用生成的参数后验样本即可估计出最终的模型参数值。

该过程通过WinBUGS软件的MCMC算法和Gibbs抽样算法实现。在根据贝叶斯方法进行参数的后验样本估计时，为了保证迭代收敛以得到稳定的参数后验概率值，本研究设定的迭代次数为1 000万次，其中每隔1 000次迭代记录一次样本数据，共搜集了10 000个样本。图2展示了模型中部分参数(a1，a2，a3)的迭代轨迹，可以看出，大约经过100次样本记录(即10万次迭代)之后所有参数趋于收敛，此时前面不收敛的10万次迭代称为退火迭代。在选取后验样本进行参数估计时需要排除退火迭代的影响，因此本研究截取了迭代100万次之后所记录的共计9 000个后验样本，得到的部分参数(a1，a2，a3，a4)的后验密度如图3所示。利用后验样本估计最终转移矩阵模型的全部参数，结果见表3。

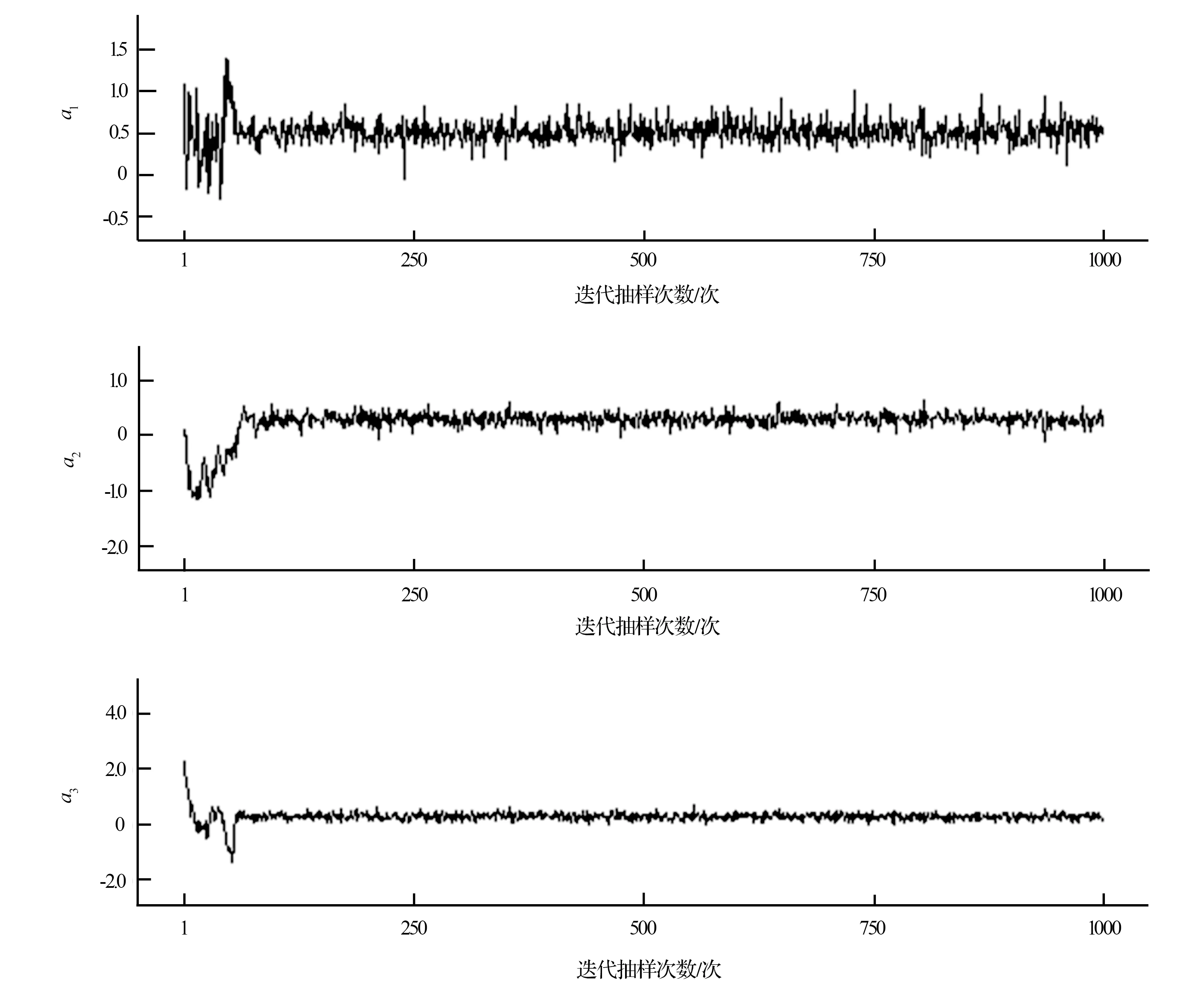
图2 部分参数迭代轨迹

3.3 模型比较

利用上述两种模型的参数结果所建立的转移概率矩阵模型对该林分2013年的径级分布进行预测，将预测结果与测试样本中2013年的真实结果进行比较，以此判断两种模型预测的准确性。

两种模型预测的径级分布与实际分布如图4所示。可见，在小径级(4～8 cm)和大径级(48 cm以上)处，两模型的预测值与真实值差异不大；对于中径级(12～44 cm)立木数量的预测分布，贝叶斯模型的预测值与真实值较接近，而固定参数模型的预测值比贝叶斯模型的预测值和真实值都要偏大。因此，贝叶斯模型比固定参数模型的预测效果更好。图5反映了两种模型的预测值与林分分布真实值之间的差异，图中的对角线表示预测值与实际观测值的等值线。可以看出，固定参数模型的预测值绝大多数分布在等值线左上方，贝叶斯模型的预测值则在等值线附近轻微波动。这进一步证明了固定参数模型的预测值比真实值偏高的趋势，而贝叶斯模型则较精确地预测了林分的真实分布。

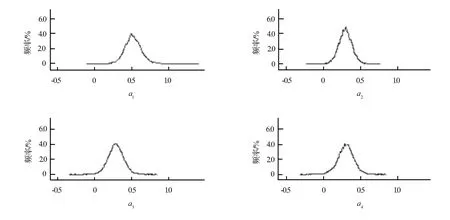
图3 部分参数的后验密度

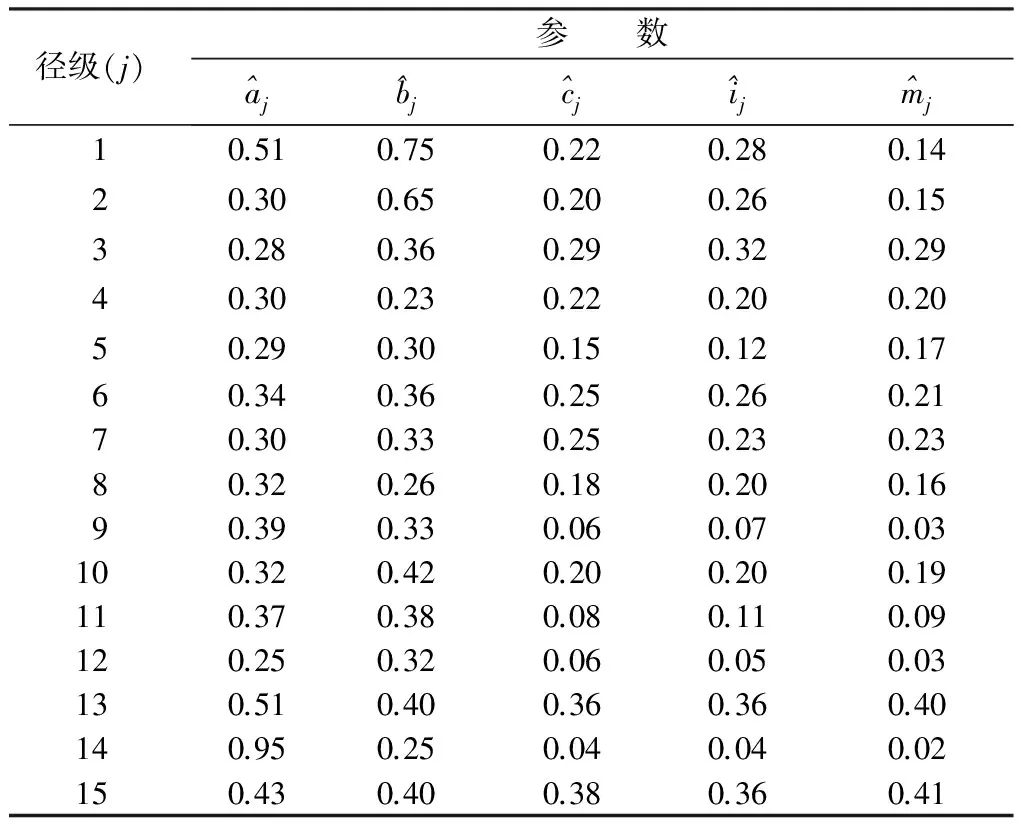
表3 贝叶斯模型的参数估计

为了更加科学地衡量两种模型的预测效果，分别计算了两种模型预测结果的均方误差MSE、均方根误差RMSE以及平均绝对百分误差MAPE，结果见表4。

可见，贝叶斯模型的各项指标均小于固定参数模型，说明贝叶斯模型的预测效果优于固定参数的模型。

表4 模型预测效果指标

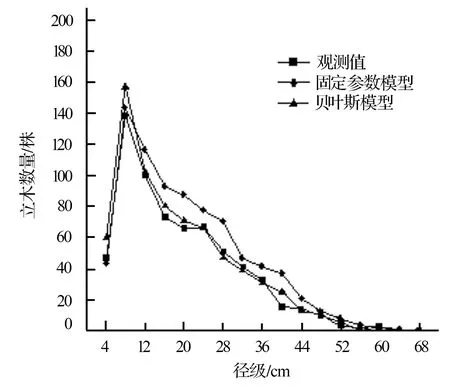
图4 两种模型的预测分布与观测分布

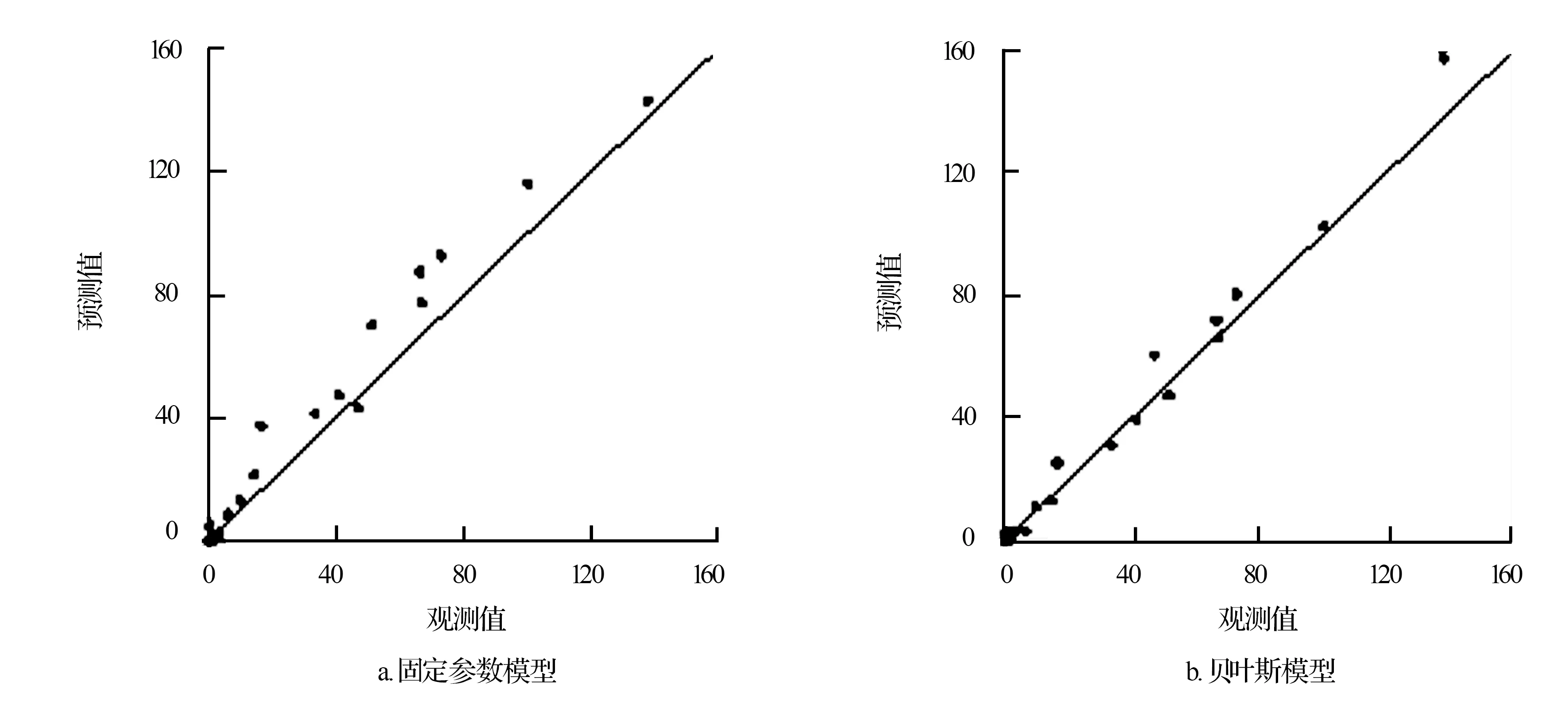
图5 两种模型预测值与观测值的比较

4 结论与讨论

采用固定参数平均的方法所建立的转移矩阵模型在进行实际林分结构预测时容易产生比实际值偏高的预测结果，而采用贝叶斯方法所建立的模型则没有这种趋势。与经典统计学方法相比，贝叶斯方法有效提高了模型的预测精度，是一种更好的模型参数估计方法。

从贝叶斯方法的参数估计过程可以看出，其利用先验信息和样本信息计算后验分布的方法可有效利用定期更新的样本数据不断调整模型参数的后验分布，从而得到更符合实际的模型参数。该方法特别适合类似于森林资源连续调查的数据，每一次调查分析的结果都可以作为下一次调查分析的先验信息，使得调查数据得到了充分的利用。因此，贝叶斯方法很适合在一些林业数据的模型参数估计上进行推广应用。

尽管如此，贝叶斯方法目前仍存在一些不足之处。其计算后验密度的方法需要依赖大量的随机模拟实验，尽管MCMC法结合Gibbs抽样算法可以有效减少计算后验密度的运算量，但随着模型参数数量的增加，随机马尔科夫链收敛的速度逐渐变慢。因此，对于参数较多的模型采用贝叶斯方法进行建模尚存在一定的局限性。这种局限性会随着计算机计算能力的发展以及算法的优化逐步被打破。

[1] 张雄清，张建国，段爱国.基于贝叶斯法估计杉木人工林树高生长模型[J].林业科学，2014,50(3):69-75.

[2] 贾乃光.贝叶斯统计学及其应用于林业的前景[J].北京林业大学学报，1988(4):91-96.

[3] 张雄清，张建国，段爱国.杉木人工林林分断面积生长模型的贝叶斯法估计[J].林业科学研究，2015,28(4):538-542.

[4] 姚丹丹，雷相东，张则路.基于贝叶斯法的长白落叶松林分优势高生长模型研究[J].北京林业大学学报，2015,37(3):94-100.

[5] 张玉环，张青，亢新刚，等.异龄针阔混交择伐林均衡曲线的确定方法：以金沟岭林场样地数据为例[J].北京林业大学学报，2015,37(6):53-60.

[6] LESLIE P H . On the use of matrices in certain population mathematics[J]. Biometrika，1945,33(5):183-212.

[7] USHER M B. A matrix approach to the management of renewable resources, with special reference to selection forests[J]. Journal of Applied Ecology，1966,3(2):347-348.

[8] BUONGIORNO J, PEYRON J L, HOULLIER F, et al. Growth and management of mixed-species, uneven-aged forests in the French Jura: implications for economic returns and tree diversity[J]. Forest Science，1995,41(3):397-429.

[9] SOLOMON D S, HOSMER R A, HAYSLETT H T . A two-stage matrix model for predicting growth of forest stands in the Northeast[J]. Canadian Journal of Forest Research，1986,16(3):521-528.

[10] YUE C H, KLDTKE J, LENK E. Ein verfahren zur bestimmung zielorientierter gleichgewichtskurven im plenterwald[J]. Berichte der Sektion Biometrie und Informatik im DVFF，1997,174:145-154.

[12] 赵俊卉，亢新刚，张慧东，等.长白山3个主要针叶树种的标准树高曲线[J].林业科学，2010,46(10):191-194.

[13] 刘洋，亢新刚，郭艳荣，等.长白山主要树种直径生长的多元回归预测模型:以云杉为例[J].东北林业大学学报，2012,40(2):1-4.

[14] 胡云云，闵志强，高延，等.择伐对天然云冷杉林林分生长和结构的影响[J].林业科学，2011,47(2):15-24.

[15] HUANG S. Diameter and height growth models[D]. Edmonton: University of Alberta,1992.

[16] ALBERT J. Bayesian computation with R[M]. New York： Springer Science & Business Media,2009.

[17] 张伟.基于MCMC的贝叶斯模型平均组合预测方法及其在我国能源消费预测中的应用研究[D].重庆：重庆师范大学,2011.

[18] SPIEGELHALTER D, THOMAS A, BEST N. WinBUGS user manual[M]. Cambridge: MRC Biostatistics Unit，2003.

[19] CHIB S, GREENBERG E. Understanding the Metropolis-Hastings algorithm[J]. American Statistician，1995,49(4):327-335.

[20] KABACOFF R,陈钢，肖楠，等.R语言实战[M].北京：人民邮电出版社,2016.

Bayesian Method in Estimating Model Parameters to Predict Diameter Class Distribution of Stand-Taking Sample Plot Data in Jingouling Forest Farm as Example//

Yu Ruchuan, Zhang Qing
(Beijing Forestry University, Beijing 100083, P. R. China);
Yue Chaofang
(Forest Research Institute of Baden-Wurttemberg, Freiburg 79100, F. R. Germany);
Kang Xingang
(Beijing Forestry University)//Journal of Northeast Forestry University，2017,45(6)：30-35.

Transition matrix model; Stand diameter class distribution; Bayesian statistics; MCMC method; Gibbs sampling algorithm

1)“948”国家林业局引进项目(2013-4-66)。

于汝川，男，1991年9月生，北京林业大学理学院，硕士研究生。E-mail：yuruchuan@qq.com。

张青，北京林业大学理学院，教授。E-mail：zhangq@bjfu.edu.cn。

2017年2月27日。

S758.5

责任编辑：戴芳天。

With the observed data in five different years from 26 sample plots in Jingouling Forest Farm of Wangqing Forestry Bureau, Jilin Province, transition matrix models were established to predict the stand diameter class distribution in a given period. Parameters of the models were estimated by classical statistical method and Bayesian method, respectively. After the fixed parameter model and the Bayesian model were built, their prediction results could be compared to test the prediction accuracy of the two models. The predicted values of fixed parameter model tend to be higher than the true value. The prediction of Bayesian model is relatively more accurate than that of fixed parameter model.