丢番图平方和恒等式的探索之旅——体现数形结合思想的一则教学案例

浙江师范大学教师教育学院 (321004) 王 安 师晓莉 朱 哲

丢番图平方和恒等式的探索之旅
——体现数形结合思想的一则教学案例

浙江师范大学教师教育学院 (321004)
王 安 师晓莉 朱 哲

在中学数学教学中挖掘和渗透数学思想方法有非常重要的意义.近年来的高考越来越重视对数学思想方法的考察.经历过数学竞赛培训的考生，大都掌握了一些高中课本所不曾接触过的知识和数学思想方法，在高考应对某些难度很大的问题时往往轻车熟路，应对自如.例如在高中数学竞赛中经常会出现恒等式的证明，求代数式的最值等问题，此时应用丢番图平方和恒等式可以在解决问题时迅速挖掘出题目中的隐含条件，从而为解决难题提供捷径.数学竞赛的思想方法可以渗透到高考题中，使问题解决更巧妙.本文借助一道高中竞赛题设计了一个渗透“数形结合”思想的教学案例，从一般到特殊，在高三复习课时以专题形式展开，在代数中融入几何，培养学生数形结合的思想，将抽象思维变为形象思维，有助于把握数学问题的本质[1]，对解决高考难题有所启发和帮助.

1.呈现问题情境

通过一个较简单的高中竞赛题引出丢番图平方和恒等式，让学生先独立思考再相互讨论.然后给出历史上丢番图的做法，通过呈现丢番图平方和恒等式产生的数学史背景，简单介绍“代数之父”丢番图的著作《算术》以及其生平，引导学生了解其发展的过程，追根溯源，让学生回到历史之中，激发探索挑战的兴趣.

问题 若两个不相等的自然数a、b使得等式(42+62)(32+52)=a2+b2成立，且a>b，则符合条件的数对有(a,b)= .(1991年广西省高中数学竞赛题)

历史上也曾对类似的问题进行过讨论，斐波那契在《平方数之书》中明确指出丢番图曾在其著作《算术》第三卷的第19个问题中写过一个算式：65=13×5=(32+22)×(22+12)=82+12=72+42.

据此，世人推测丢番图很早就已经掌握了这个平方和恒等式所揭示的实数运算规律，因此，这个平方和恒等式被命名为丢番图平方和恒等式，也成为后世阿拉伯人证明其他数学理论的强大工具.

引发学生思考：我们能把发现的规律用数学语言表示出来吗？

若a、b、c、d是实数，则(a2+b2)(c2+d2)=(ad+bc)2+(bd-ac)2.

根据这个公式，我们可以得出上述问题的答案：满足上述条件的数对是(38,18)或(42,2).通过解决高中数学竞赛题，了解相关数学史实，让学生经历知识形成的过程，从中获得成功的体验.

2.证明丢番图平方和恒等式

应用丢番图平方和恒等式可以在解决高中数学难题时让解法更加巧妙简便.但在学习过程中，学生对于抽象冗长的数学公式还是很难理解和记忆.因此，我们将对其进行推导证明，从一般到特殊，逐步加深学生对丢番图平方和恒等式的理解，为之后的应用打下良好的基础.

在初中阶段学生就已经学习了整式的乘法和相关的乘法法则，引导学生回忆学过的乘法法则和乘法公式.

①单项式与多项式相乘：a·(b+c)=ab+ac.

②两数和的平方：(a+b)2=a2+b2+2ab.

③平方差公式：(a+b)(a-b)=a2-b2等.

引导学生思考：我们可以用直观的几何图形形象地表现这些代数恒等式吗？让大家动手画一画，然后教师通过几何画板向学生进行展示，具体见图1，图2，图3.

图1 图2

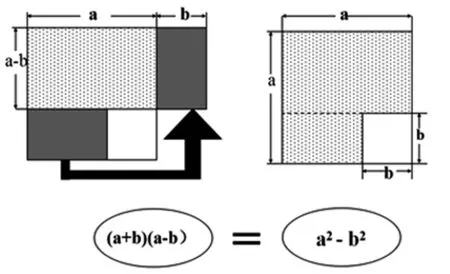
图3

通过几何画板演示图形，在学生头脑中初步构建了数形转化的模型，重点关注平方差公式.与前面两个公式不同的是平方差公式在代数式转变成面积的基础上，还要通过剪切拼接才能得到最后的结果，让学生好好体会其中蕴含的数学思想方法，从一般到特殊，为下面丢番图平方和恒等式的证明做好铺垫.

接下来，教师提出更有挑战性的问题.呈现丢番图平方和恒等式：(a2+b2)(c2+d2)=(ad+bc)2+(bd-ac)2.

引导学生思考：古希腊的几何成就斐然，在丢番图之前已经涌现出了许多几何大师，那么丢番图平方和恒等式是否也蕴含了几何背景呢？你能给出这个复杂的代数恒等式合理的几何解释吗？

教师提出问题后，学生先独立思考，然后小组交流相互补充，每个小组派代表来展示一下证明过程，鼓励学生用多种方法进行证明.如果学生感到有困难，教师可以引导学生回忆用面积法证明平方差公式时，关键是用a,b表示出图中相关正方形和长方形的面积，再找到它们之间的等量关系，由此迁移到丢番图平方和恒等式的证明.

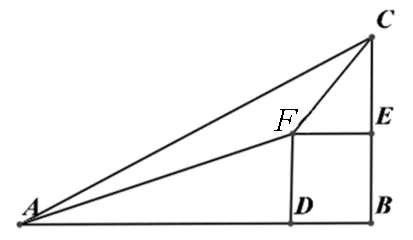
图4

(1)几何证法一

如图1所示，在RtΔABC中，设AB=c,BC=d,AD=b,BE=a.则DB=c-b，CE=d-a.过点D、E分别作直角边AB、BC的垂线，使它们交于点F，于是四边形DBEF是矩形.

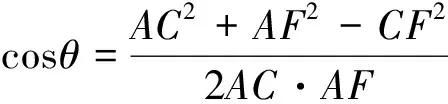
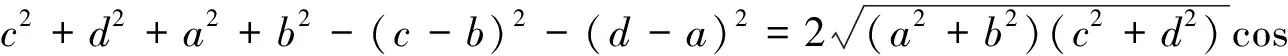
因此(a2+b2)(c2+d2)=(bc+ad)2+(a2+b2)(c2+d2)sin2θ.

又因为SΔACF=SΔABC-SΔADF-SΔCEF-S1(其中SΔACF、SΔABC、SΔACF、SΔCEF、S1分别表示各个三角形的面积以及矩形DBEF的面积.)因此

这个证明过程涉及的几何知识并不难，只是运算稍微繁琐一些，通过数形结合，揭示了丢番图平方和恒等式的几何背景.

(2)几何证法二

引导学生思考：几何证法一中丢番图平方和恒等式的证明推导过程虽然思路简单，但是需要进行大量运算，能否只通过直观的形来揭示抽象的数的本质，达到“不证自明”？

丢番图平方和恒等式其实有着非常直观的几何背景，观察如图5-图10所示的一系列图形就可以“不证自明”[2].

首先引导学生观察恒等式的左右两边各有什么特点，左端很容易让人联想到矩形的面积公式.因此，图5把丢番图平方和恒等式的左式转化成了一个长为(a2+b2)，宽为(c2+d2)的矩形面积表达式，十分巧妙地将抽象的代数式转化成了直观的图形，与学生熟知的矩形面积联系在一起，增加了亲切感；图6在图5的基础上将各个矩形面积转化成了相对应的4个边长分别为ac、bc、ad、bd的正方形的面积；图7在图6的基础上，将正方形进行了重新拼接；图8把图7右侧的图形进行新的剪拼，为图9的转换做好准备；图9将面积为abcd的矩形的长和宽进行了重新的转换，恰好与图8左侧的图形拼接组成了一个边长为(ab+dc)的正方形；图10则展示了最后拼接的结果，我们可以很直观的看到通过一系列巧妙的剪割拼接，最后得到了一个面积为(ab+dc)2的正方形，和一个面积为(bd-ac)2的矩形.

通过数形完美的结合，用直观的形来揭示数的本质，与几何证法一相比更直观，且避免了代数运算的繁琐，达到“不证自明”的效果.另外，这种证法与导入平方差公式时给出的证明思想方法基本一致，让学生学会迁移，举一反三，加深对丢番图平方和恒等式的理解，学会数形结合的思想方法.

通过提供多种证明方法，由学生进行选择，培养学生学习的主动性，开阔学生的思路，同时渗透数形结合思想，也是分散，分步突破本节的重难点，引导学生学习时知识的正迁移，让学生惊叹于数形转化之妙的同时，巧妙解决问题，增强探索数学的兴趣.

3.丢番图平方和恒等式在高中数学中的应用

在经历了丢番图平方和恒等式证明的探究之后，学生对其有了更深刻的理解，对数形结合也有了进一步的认识.因此，通过一些练习来进行应用巩固，让学生感受其在数学解题中发挥的巨大价值.

3.1 用丢番图平方和恒等式证明二维柯西不等式

思考：你能用丢番图平方和恒等式证明二维柯西不等式吗？

二维柯西不等式：若a,b,c,d∈R,则(a2+b2)(c2+d2)≥(ac+bd)2.

出示问题后，先让学生独立思考，然后小组之间交流讨论，请一位同学上台来展示一下他的做法，教师给予及时的点播和纠正，并给予鼓励.

证明：∵a,b,c,d∈R,∴(ad-bc)2≥0,∵(a2+b2)(c2+d2)=(ac+bd)2+(ad-bc)2,∴(a2+b2)(c2+d2)≥(ac+bd)2.

通过丢番图平方和恒等式的简单应用来证明二维柯西不等式，由于思路清晰，一步到位，大部分学生都能在解决问题的过程中体会到成功的喜悦.

3.2 用丢番图平方和恒等式解决高中数学竞赛题

对于优秀的学生，用丢番图平方和恒等式解决高中数学竞赛题来开发他们的数学潜能.

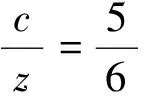
由于个体存在差异性，对于班级里优秀的学生，通过此题能进一步强化对丢番图平方和恒等式的理解，提高学生的思维能力和计算能力.利用丢番图平方和恒等式解决高中数学竞赛题，不仅可以让学生领会数形结合的思想方法，而且让学生面对高考难题时也会进行迁移，充满挑战的信心.

[1]葛益平.数形结合在高中数学中的妙用[J].中学数学.2016,(9):65-68.

[2]RogerB.Nelsen.数学写真集(第一季)——无需语言的证明[M].机械工业出版社，2016：22.

[3](美)G·波利亚著.涂泓，冯承天等译.怎样解题——数学教学法的新面貌[M].上海科技教育出版社,2002.

[4]朱哲.余弦定理：一则体现数学联系与历史的教学案例[J].数学通讯, 2005(17):1-3.

[5]欧阳绛.数学方法溯源[M].大连理工大学出版社,2008.