空间直线与平面平行问题的二型四策

甘肃省临泽一中 (734200) 张元国

空间直线与平面平行问题的二型四策

甘肃省临泽一中 (734200)
张元国

空间直线与平面的平行问题，是近年高考命题经久不衰的热点.如何巧妙迅捷的判定空间直线与平面平行，如何在平面内寻找一条直线，以静制动，探索该直线与平面平行，本文给出两种常见类型的四种推证策略.

1.判定空间直线与平面平行

1.1 作平行平面

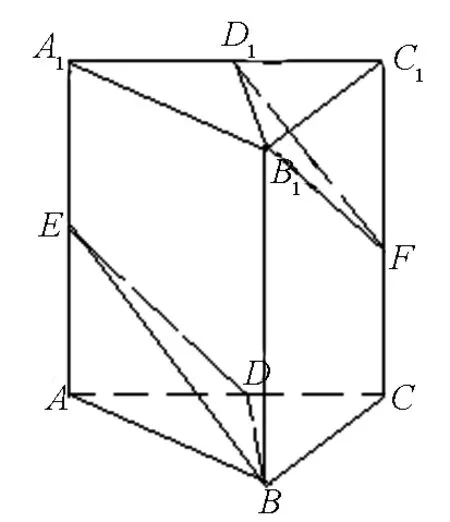
图1

例1 三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC，D,E,F分别为棱AC，AA1，CC1的中点.求证：B1F∥平面BDE.

分析:如图1，取A1C1中点D1，则B1D1∥BD.又D1F∥A1C，DE∥A1C,知D1F∥DE.从而平面B1D1F∥平面BDE，又B1F⊄平面BDE，故B1F∥平面BDE.

评注:判定直线与平面平行时，若能找到一个平行平面，则可利用面面平行迅捷推证线面平行.

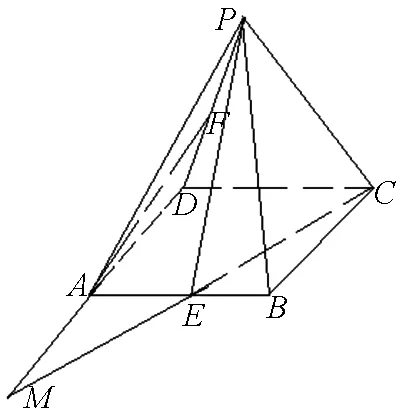
图2

1.2 作三角形截面

例2 四棱锥P-ABCD的底面ABCD为菱形，E,F分别是AB,PD的中点.

求证：AF∥平面PEC.

分析:如图2，过五点A,F,P,E,C外的一点D，连DA,DF分别交平面PEC于点M与P，即延长DA，CE相交于点M.只需证AF∥PM.

评注:判定直线与平面平行，关键是在平面内找一直线与平面外的直线平行.若能在确定该平面的点与确定该直线的点外再找到一个点，并过该点作一个三角形截面，则可巧妙地找到与平面外的直线平行的平面内直线，然后利用线段成比例，就能巧证线面平行.

1.3 作平行四边形截面

例3 四棱锥P-ABCD的底面ABCD为菱形，E,F分别是AB,PD的中点.求证：AF∥平面PEC.

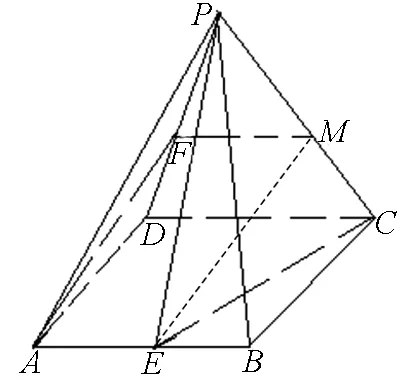
图3

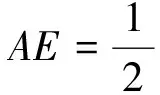
由FM,知

AEFM.即四边形AFME为平行四边形.从而EM∥AF，又AF⊄平面PEC，故AF∥平面PEC.

评注:判定直线与平面平行时，若能经过平面外的直线上两点作一个与该平面都相交的平行线，就可巧妙地找到与平面外的直线平行的平面内的直线.然后通过推证该平面四边形是平行四边形，就能巧证直线与平面平行.

1.4 利用平面向量基本定理

例4 在三棱柱ABC-A1B1C1中，D,E分别为AA1,B1C的中点.求证：DE∥平面ABC.

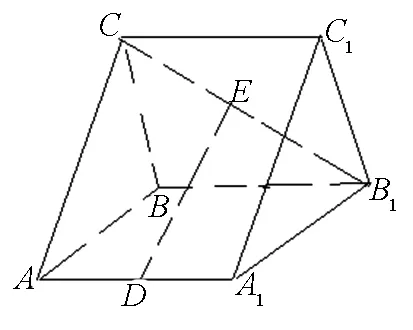
图4

评注:判定直线与平面平行时，若能利用平面向量基本定理，选择基底，进行向量分解，就可利用代数方法巧证直线与平面平行.

2.探索直线与平面平行

2.1 作三角形截面

例5 四棱锥P-ABCD的底面ABCD为直角梯形，AB∥DC，AB=3DC=3，在棱PB上确定一点E，使得CE∥平面PAD.

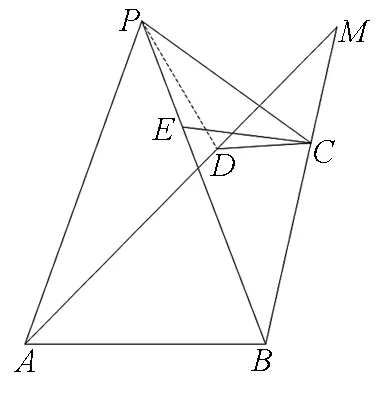
图5

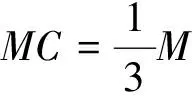
评注:探索直线与平面平行，若能在确定该平面的点与确定该直线的点外再找到一个点，并过该点做一个三角形截面，则可巧妙地找到与平面外的直线平行的平面内的直线，迅捷推证.

2.2 作平行平面

例6 四棱锥P-ABCD的底面ABCD是菱形，PA=3，F在棱PA上，AF=1，E在棱PD上.若CE∥平面BDF.求PE∶ED的值.

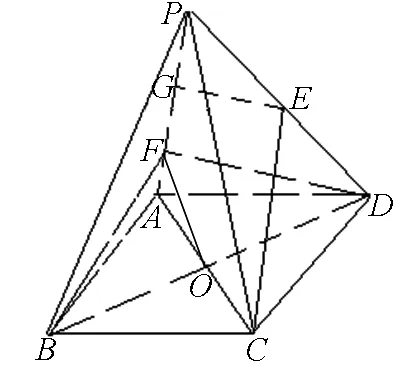
图6

分析:如图6，设AC与BD交于O，过点E作EG∥FD交PA于G.又CE∥平面BDF,知平面CEG∥平面BDF,得CG∥平面BDF.

又平面CGA∩平面BDF=OF,知CG∥OF.由O为AC中点，F为AG中点.∴GF=AF=1,由PA=3,知PG=1.∴G为PF中点，从而E为PD中点，即PE∶ED=1∶1.

评注:探索直线与平面平行，若能找到一个平行平面，则可利用面面平行迅捷得到线面平行.

2.3 作平行四边形截面

例7 几何体EFG-ABCD的底面ABCD是平行四边形，EF∥AB，FG∥BC，EG∥AC，AB=2EF.在线段AD上是否存在一点M，使GM∥平面ABFE.

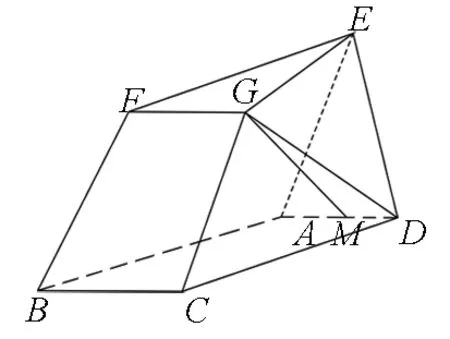
图7

分析:如图7，过两点G,M作两平行线均与平面ABFE相交.

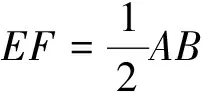
评注:探索直线与平面平行，若能经过平面外的直线上两点作一个与该平面都相交的平行线，就可迅捷找到与平面外的直线平行的平面内的直线.

2.4 利用平面向量基本定理

例8 四棱锥P-ABCD的底面ABCD为直角梯形，AB∥DC，AB=3DC=3，在棱PB上确定一点E，使得CE∥平面PAD.

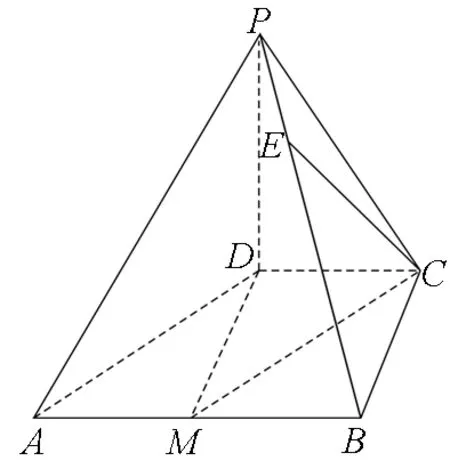
图8

分析:如图8，过D作DM∥CB交AB于M，则DM=CB.

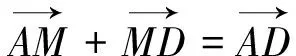
评注:探索直线与平面平行时，若能利用平面向量基本定理，选择基底，进行向量分解，就可利用代数方法巧证线面平行.