基于压缩感知的快速SIFT准稠密匹配算法

张 霓，章承成，何熊熊

(浙江工业大学 信息工程学院，浙江 杭州 310023)

基于压缩感知的快速SIFT准稠密匹配算法

张 霓，章承成，何熊熊

(浙江工业大学 信息工程学院，浙江 杭州 310023)

提出了一种基于压缩感知的SIFT准稠密立体匹配算法.该算法利用压缩感知理论的稀疏投影将SIFT的高维特征描述子投影到低维空间上，选取RANSAC算法对匹配的结果进行去伪匹配处理，并将提取的匹配点作为种子点沿着极线方向生长，获取稠密的视差图.该算法利用压缩感知的稀疏投影，大大减小了特征匹配的运算量，同时利用种子生长使视差图变稠密.实验结果表明：与未加入压缩感知的种子扩散立体匹配算法相比，这种算法计算速度更快，误匹配的百分比也较低，是一种快速有效的立体匹配算法.

SIFT；压缩感知；RANSAC；立体匹配；种子扩散；视差

立体匹配[1]一直是计算机视觉中的热点问题，其目的是寻找左右两幅图像中的对应点以计算视差，获取物体的深度信息，匹配结果的好坏直接影响后面三维重建的准确性.立体匹配算法主要分为稠密匹配、稀疏匹配和准稠密匹配.稠密匹配是指通过相关的一些算法来获取大量的匹配对，生成致密的视差图[2].经典的稠密匹配算法有基于区域的立体匹配算法，如灰度差绝对值平方和(SAD)算法[3]、归一化互相关(NCC)算法[4]以及Census[5]变换算法等，这些稠密立体匹配算法直接对图像像素点进行匹配，虽可获得稠密的视差图，但计算复杂度高，在光照变化的情况下，会发生左右两幅图像幅度失真，其匹配精度会急剧下降.而稀疏匹配是指基于特征的匹配算法，这类立体匹配算法计算量小，速度快，匹配精度高.但由于匹配的是图像中的一些特征点，只能得到稀疏的视差图，通过它们只能恢复出稀疏点云，不能有效恢复三维立体表面[6].准稠密匹配算法[7]是介于稠密匹配和稀疏匹配之间的一种立体匹配算法，它克服了两者的缺点，可以得到比稀疏匹配更为稠密的匹配点，且比稠密匹配的计算量的小、复杂度低.Lhuillier等[7]提出的准稠密匹配算法是利用稀疏的匹配点，将其作为种子点并在其周围扩散出更多的匹配点.稀疏种子点的获取是准稠密匹配算法的核心组成部分.SIFT算法[8]是目前广泛应用的一种鲁棒性最好的特征提取和匹配的算法，因SIFT算子对旋转、尺度和光照都具有不变性而在立体匹配中得到广泛应用.但SIFT算法的特征描述子维数过高，计算速度慢，不能满足实时性要求.近年来,压缩感知理论[9-11]也开始被引入到立体匹配邻域中.Eva等[12]将CS引入特征提取中，直接从感知测量值中重建感兴趣的图像特征，丢弃不相关的信息.杨飒等[13]将压缩感知应用到图像配准中，提出了稀疏投影与SIFT结合的图像配准算法(SRP-SIFT)，用稀疏投影矩阵对特征点周围的局部小块的特征进行降维，减少了算法的复杂性.

为了克服基于SIFT的立体匹配算法计算量大、不能获取稠密的视差图的问题，提出了一种用于已标定图像的快速准稠密立体匹配算法.首先使用SIFT对图像提取特征点，通过压缩感知的随机投影来降低SIFT的特征向量的维数，在不丢失特征主要信息的前提下提高了特征匹配的速度；然后将匹配点作为种子点扩散到整幅图像上，得到稠密的视差图.最后将实验结果(基于压缩感知的SIFT算法加种子扩散算法)与SIFT算法加种子扩散算法进行比较，证明本算法在降低算法复杂性的同时还保证了视差图的质量.

1 算法思路

本算法基于压缩感知原理，首先使用SIFT算法检测图像的特征点，然后用压缩感知对获取的特征点降维，获取低维的特征向量，再用RANSAC算法对获取的匹配点去除误匹配来得到用于区域增长的种子点；最后沿着极线方向对这些种子点进行扩散，并把新增的匹配点作为新的种子点，以此类推，最终得到稠密的匹配图和视差图.算法的流程图如图1所示.

图1 算法流程图Fig.1 Algorithm flowchart

2 基于压缩感知的SIFT种子点提取

基于压缩感知的SIFT立体匹配算法的第一步是用SIFT算法获取种子点，并对种子点进行匹配，种子点匹配的准确与否以及匹配速度直接影响了算法的性能.针对SIFT算法的特征向量多，计算复杂等问题，将SIFT局部特征提取与压缩感知稀疏投影相结合，先用SIFT算法提取参考图像与待测图像的局部特征，然后采用压缩感知的随机投影将特征向量投影到低维空间上，再进行特征匹配.

2.1SIFT特征提取

本算法采用SIFT算法提取图像的局部特征，具体步骤如下：

1) 建立尺度空间.利用不同尺度空间的差分与图像的卷积来建立高斯差分尺度空间(DOG)，可得

D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))×I(x,y)=L(x,y,kσ)-L(x,y,σ)

(1)

式中：I(x,y)为原始图像；G(x,y,σ)为高斯核；σ为尺度因子，该值越小表示图像平滑的越少，相应的尺度也越小，Low[8]的论文中初始尺度σ=1.6；L代表图像的尺度空间.

2)特征点检测与精确定位.将每个采样点与它相邻26个点比较(同尺度8 个、上下相邻尺度9 个×2 个)[8]，选取最大值或最小值点为候选特征点；用三维二次拟合函数来得到特征点的精确位置；同时去除不稳定的边缘极值点和对比度低的点，以增强匹配的稳定性和抗噪声能力.

3)特征点的方向.由特征点邻域像素的梯度的幅值m(x,y)和方向((x,y)来指定特征点的梯度方

向参数，其中L函数与式(1)中的L函数一样同为图像的尺度空间，计算式为

(2)

θ(x,y)=tan-1((L(x,y+1)-L(x,y-1))/ (L(x+1,y)-L(x-1,y)))

(3)

4)特征描述子生成.为了增强算法在实验中的稳健性，Low[8]建议对每个特征点采用4 个×4 个种子点来描述，每个种子点含有8 个方向的信息向量，这样每个特征点的特征向量就有128 维.

2.2 基于压缩感知的特征压缩

由于SIFT算法获取的种子点的特征向量可高达128 维，而进行SIFT特征匹配时必须要计算参考图像中的特征点与待匹配图像中每一特征点的距离，而这每一个距离都包含了到128 维的数据，这直接导致了匹配时的大计算量.为了实现数据的快速匹配，这里引入压缩感知算法，采用随机投影矩阵将高维的特征描述符投影到低维空间上以降低算法的复杂度，减少算法运行的时间.

将已经获得的128维×1维列向量F稀疏表示为

F=ΨX

(4)

(5)

式中：X为128维×1维列向量；若X中有k个不为零的系数，则信号X的稀疏度为k；fi为F的元素；xi为X的元素；φi为Ψ的行向量.构建一个M维×128维稀疏随机投影矩阵R将128维×1维的描述子投影到M维的子空间中，Y为得到的随机测量值，得

YM×N=RM×128X128×N,M≪12

(6)

这样每个特征点的信息就包含在了维的特征向量中.为了兼顾随机投影的有效性，同时又能够减少计算的复杂度，这里选择s=3，R的矩阵元素为

(7)

2.3 基于压缩感知的特征匹配

特征描述子降维之后，选择计算描述子之间的欧式距离作为相似性度量，同时采用最近邻与次近邻比值法[14]对特征向量进行匹配.设点A的特征描述向量为UA=[a1,a2,…,am]，点B的特征描述向量为UB=[b1,b2,…,bn]，则UA和UB的绝对值距离为

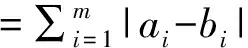
(8)

在待匹配图中找出与参考图像的特征点的描述子距离最近与次近的点B与点C，若d(UA,UB)/d(UA,UC)的比值T小于某个阈值时，则匹配成功.这里设置的阈值为0.6.最后使用随机一致性(Random sample consensus, RANSAC)[15]算法去除由于自身对称性可能造成的误匹配点.

3 稠密视差图的计算

至此，匹配的过程基本结束，接下来要实现匹配得到的视差图，由于SIFT特征匹配算法只是完成了离散的特征点匹配，得到的是稀疏的匹配的特征点和稀疏的视差图，无法获得完整的图像匹配点信息.为了得到连续的匹配点和稠密的视差图，同时减少扩散时间，这里将已获取的匹配点作为种子点，采用加入极线约束的扩散算法对种子点进行扩散，直至遍历整个图像，使视差图成为一个致密的图.

种子点扩散[16-17]的步骤：将通过RANSAC去除误匹配之后的稳定的匹配点对作为种子点，按照顺序将它们放入种子队列中；若队列非空，取出队列中第一对种子点，在其邻域的一定搜索窗内寻找匹配点，找到匹配点后就将该对种子点从队列中删除，将获取的新种子点放入种子队列的末尾中，重复此步骤直至种子队列为空.为了提高搜索效率，这里引入极线约束[18](即匹配点一定在对应的极线上)，由于这里用于实验的图像都是经过校准后的，因此它的匹配点的两条极线在图像的同一条行扫描线上.这样就可以将二维的搜索窗变为沿着一维的极线方向，对左图中已确定的种子点，在右图中按照相应的极线的方向上进行种子点的扫描扩散，这样可以大大减少扩散的时间.

其中搜索种子点主要是通过对SIFT计算出的视差建立一个能量函数[19],即

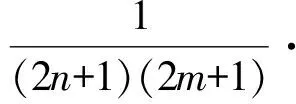
(9)

式中：d为已匹配的特征点的视差；i为图像的高度；j为图像的宽度；L(i,j)，R(i,j)分别为左右图像中点(i,j)的灰度值，若该能量值小于一定的值，则认为该点属于种子点，扫描直到极线结束，最终获得稠密的视差图.

4 实验分析

在实时性要求较高的应用中，好的立体匹配算法不仅需要获取准确的匹配率以及高质量的视差图，同时还要兼顾算法的运算量，而算法的运算量是和特征描述子的维数息息相关的.因此为了验证算法的有效性，实验一将SIFT算法与基于压缩感知的SIFT算法从提取的匹配点的数目、准确率以及匹配时间上比较；实验二将SIFT+种子扩散算法与基于压缩感知的SIFT+种子扩散算法这两种算法从匹配的视差图的好坏、匹配的时间上做比较.实验图片选用Middlebury数据库中的Teddy图片[20].实验中，软件工具是Win7 32位操作系统，MATLABR2010b编程环境，硬件环境是Corei3，CPU2.4GHz，4GB内存.图2为实验选取的图像.

图2 原图像Fig.2 Original image

图3(a)为SIFT算法获取的作为种子点的匹配点对的匹配结果，图3(b)为提出的基于压缩感知的SIFT算法获取的种子匹配点对.表1为这两种方法提取种子点的时间及准确率比较.从图3和表1的数据可以看出：加入压缩感知的SIFT算法匹配成功的点数比SIFT算法少，但匹配速度比SIFT算法快，这是由于使用了压缩感知的稀疏变换来构成低维数的特征描述符，减少了SIFT描述子匹配时的计算量，所以匹配时间大大减少.同时，该方法通过RANSAC算法可以自行剔除错误匹配对，匹配准确率也较SIFT算法有一定提高，使得其作为扩散的种子点更稳定.

图3 种子点提取的实验结果比较Fig.3 Comparison of experimental results of extraction of seed dots

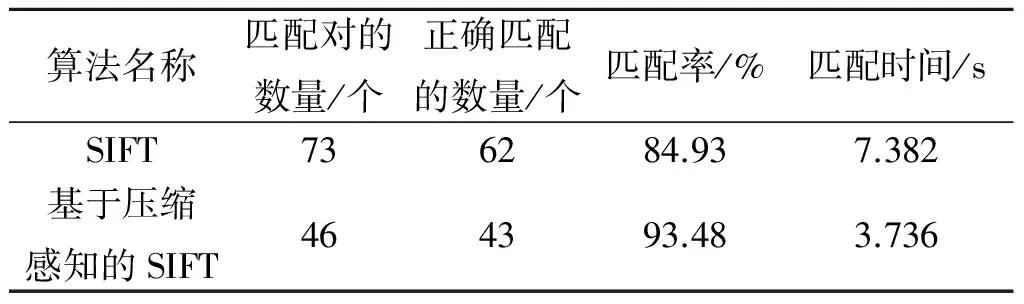
算法名称匹配对的数量/个正确匹配的数量/个匹配率/%匹配时间/sSIFT736284．937．382基于压缩感知的SIFT464393．483．736

图4(a)为teddy图片的标准视差图，图4(b，c)分别为SIFT+种子极线扩散算法以及SIFT+压缩感知+种子极线扩散方法得到的视差图.从图4的结果来看：基于SIFT特征的两种种子扩散匹配算法，都可以取得比较令人满意的扩散结果.同时，这两种算法即特征匹配与种子极线扩散结合的算法由于沿极线方向扩散，加快了扩散的速度，减小了计算冗余，整体算法时间都不长，SIFT+种子扩散算法的整体运行时间为26 s，而本算法由于在SIFT特征匹配时还加入了压缩感知，运行时间仅为15 s，更进一步的提高了整体的匹配速度.

图4 立体匹配视差图比较Fig.4 Comparison of disparity maps of stereo matching

5 结 论

传统的稠密立体匹配算法匹配速度慢，而基于特征的稀疏立体匹配算法获得视差图不够稠密，且SIFT特征匹配的特征描述向量阶段的维数高、计算复杂以及运算时间长.而基于压缩感知的SIFT加种子扩散的准稠密立体匹配算法能很好的克服这些缺点，它使用压缩感知理论的稀疏随机投影对SIFT提取的128维特征描述子进行降维，大大提高了种子点的匹配速度，从而使整个算法的速度获得提高；同时使用种子扩散理论将匹配的种子点进行扩散，获取了稠密的视差图.采用SIFT+种子扩散算法、基于压缩感知的SIFT+种子扩散算法针对图像进行实验比对，结果表明：这两种算法都能获取较精确的视差图，且本算法的匹配速度明显超过未加入压缩感知的SIFT立体匹配算法.但是该算法针对的是已标定的图像，下一步的研究将是考虑把算法运用到未标定的图像中去，进一步考察本算法的匹配有效性.

[1] 汤一平，庞成俊，周宗思，等.双目全方位视觉传感器及其极线校正方法[J].浙江工业大学学报，2011,39(1):86-91.

[2] 陈友庆.基于区域增长的双目视觉三维重建技术研究[D].成都：西南交通大学,2010.

[3] 李海滨，刘婷婷，张强，等.采用自适应搜索范围的多介质立体匹配算法[J].中国科技论文，2014，9(4):456-464.

[4] WEI S D, LAI S H. Fast template matching based on normalized cross correlation with adaptive multilevel winner update[J]. IEEE transaction on image processing,2008,17(11):2227-2235.

[5] RAMIN Z, JOHN W. Non-parametric local transforms for computing visual correspondence[M]. Stockholm: Computer Vison-ECCV′94,1994:151-158.

[6] 邵琪克,陈胜勇,刘盛.基于约束扩散法匹配的序列图像三维建模研究[D].杭州：浙江工业大学,2014.

[7] LHUILLIER M, QUAN L. Match propagation for image-based

modeling and rendering[J]. IEEE transactions on pattern analysis and maching intelligence,2002,24(6):1140-1146.

[8] DAVID G L. Distinctive image features from scale-invariant keypoints[J]. International journal of computer vision,2004,60(2):91-110.

[9] DONOHO D L. Compressive sensing[J]. IEEE transaction on informational theory,2006,52(4):1289-1306.

[10] CANDES E, OMBERG J, TAO T. Robust uncertainty principles: exact signal recognition from highly incomplete frequency information[J]. IEEE transaction informational theory,2006,52(2):489-509.

[11] 于爱华,白煌,孙斌斌,等.基于优化投影矩阵的人脸识别技术研究[J].浙江工业大学学报，2016,44(4):392-398.

[12] EVA L, MONTSE N. Compressive spectrum sensing based on spectral shape feature detection[C]//Wireless Communication Systems. Barcelona: Universitat Polit`ecnica de Catalunya,2013:1-5.

[13] 杨飒,杨春玲.基于压缩感知与尺度不变特征变换的图像配准算法[J].光学学报,2014,34(11):1-5

[14] 薛振华.图像局部不变性特征提取与匹配[D].天津：天津大学,2013.

[15] WU X Q, ZHAO Q S, BU W. A SIFT-based contactless palmprint verification approach using iterative RANSAC and local palmprint descriptors[J]. Pattern recognition,2014,47(10):3314-3326.

[16] LIU R, HE L, LU K. An algorithm for image match propagation[C]//Industrial Control and Electronics Engineering(ICICEE), 2012 International Conference on. Berlin: IEEE,2012:759-762.

[17] JUHO K, SAMI S B. Quasi-dense wide baseline matching using match propagation[C]//IEEE Conference on Computer Vision and Pattern Recognition. Berlin: IEEE,2007:1-8.

[18] 葛磊.双目鱼眼镜头匹配算法研究[D].天津：天津理工大学,2014.

[19] WANG W, ZHU H. A robust quasi-dense wide baseline matching method[C]//Computational Intelligence and Security(CIS), 2015 11th International Conference on.Portland: IEEE,2015:113-116.

[20] DANIEL S, ALEXANDER V R, RICK S. Middlebury stereo vision page[DB/OL]. [2016-10-10]. http://vision.middlebury.edu/stereo/data/scenes2003/.

(责任编辑：陈石平)

Fast SIFT quasi-dense matching algorithm based on compressive sensing

ZHANG Ni, ZHANG Chengcheng, HE Xiongxiong

(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)

This paper proposes a fast SIFT quasi-dense stereo matching algorithm based on compressive sensing. By the sparse projection of compressive sensing theory, the high-dimensional feature descriptors of SIFT are projected into the low-dimensional space. The RANSAC algorithm is used to remove the false match. The extracted matching points are taken as seed points and grow along the polar line direction to obtain the dense disparity maps. This algorithm uses the sparse projection of compressive sensing to greatly reduce the amount of feature matching calculations. It also uses seed growth to make the disparity map denser. Experimental results show that the algorithm proposed in this paper is faster and the percentage of mis-matched is also lower than the seeded stereo matching algorithm without compressive sensing. It is a fast and effective stereo matching algorithm.

SIFT; compressive sensing; RANSAC; stereo matching; seed diffusion; disparity

2016-10-09

国家自然科学基金资助项目(61473262)

张 霓(1970—)，女，浙江杭州人，副教授，硕士生导师，研究方向为机器人视觉、多移动机器人协同及无人机，E-mail：zn@zjut.edu.cn.

TP391

A

1006-4303(2017)03-0310-05