基于AFSA-BPNN的MRVM模型非线性融合建模

夏陆岳，刘 勇，潘海天

(1.浙江工业大学 化学工程学院，浙江 杭州 310014；2.浙江省生物燃料利用技术研究重点实验室，浙江 杭州 310014)

基于AFSA-BPNN的MRVM模型非线性融合建模

夏陆岳1,2，刘 勇1,2，潘海天1,2

(1.浙江工业大学 化学工程学院，浙江 杭州 310014；2.浙江省生物燃料利用技术研究重点实验室，浙江 杭州 310014)

针对化工过程强非线性和多工况的特性，提出了一种基于BP神经网络(BPNN)有效非线性融合多关联向量机(MRVM)的建模方法.首先选择不同的核函数，采用样本数据建立单一RVM子模型；然后利用BPNN的强非线性拟合能力，对各子模型的预测信息进行非线性融合，并采用人工鱼群算法(AFSA)对BPNN的初始权重和阈值进行优化；最终建立MRVM非线性融合模型.将该建模方法应用于甲醇制烯烃生产过程(MTO)乙烯收率预测研究中，研究结果表明：与单一RVM模型和最优加权组合模型相比，基于MRVM的非线性融合模型具有更佳的预测精度.

MRVM；BPNN；AFSA；组合模型；非线性

软测量技术通过建立易测或可测参数与待测目标参数之间的非线性关系，以解决工业生产中重要过程变量的在线检测问题，该技术的研究核心是建模方法.目前，建模方法主要有机理建模、神经网络以及支持向量机等方法[1-2].由于化工过程的复杂性，机器学习算法在软测量中逐渐得到了广泛应用，但仍存在一些不足.关联向量机(Relevance vector machine，简称RVM)是一种基于统计学理论的新兴机器学习方法.与支持向量机相比，RVM具有关联向量个数少、待优化参数少、核函数选择不受限制、可完成概率式预测以及学习能力较强等优点，在软测量领域中具有广泛的应用前景[3-4].

单一RVM模型一般难以满足当前工艺繁杂、反应机理复杂的化工系统软测量实际研究需要，存在着过程特性匹配不佳、预测精度和外推性较差等问题.通过有效融合多个模型，可充分提取样本数据中的各种信息，以进一步增强预测模型的精度和鲁棒性，在软测量研究领域中得到了广泛应用[5].目前，多模型融合方法大多采用线性组合形式，但其并不能准确描述实际对象的非线性特征，致使预测效果不尽理想.为了能更准确地描述复杂对象的特征，可将不同预测模型所取得的预测结果进行非线性融合，以得到预测精度更佳的预测结果.本研究采用BP神经网络用于实现多个子模型的非线性融合，提出一种基于BP神经网络融合多关联向量机(MRVM)的建模方法，并将该建模方法应用于甲醇制烯烃生产过程乙烯收率软测量研究中，以验证该建模方法的有效性.

1 建模方法

1.1 设计思想

BP神经网络是一种误差反向传播的多层前馈网络.若隐含层神经元个数满足要求，BP神经网络可无限逼近任何非线性映射关系[6]，故可利用BP神经网络作为非线性组合函数，用于实现多模型的输出融合.本设计思想是通过BP神经网络用来实现多个RVM模型的非线性融合，该组合模型的构架如图1所示.该组合模型利用不同核函数的RVM模型，从各个维度提取样本数据的多样特征信息，再将各子模型输出作为BP神经网络的输入，以实现各子模型预测信息的非线性融合.

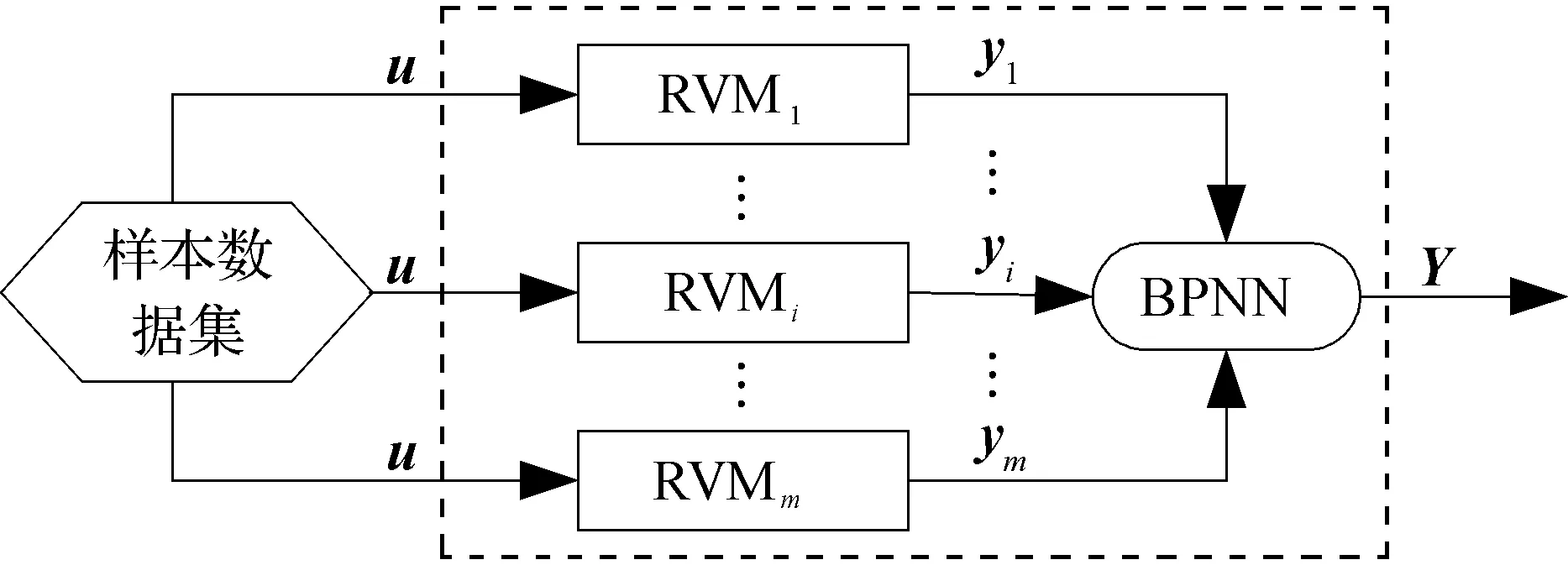
图1 MRVM非线性融合模型结构Fig.1 The structure of MRVM nonlinear combination model

在图1中，yi为第i个子模型的输出，m为子模型个数，Y为组合模型的最终输出.该组合模型的数学表达式为

Y=g(y1,y2,…,ym)

(1)

式中g(·)为非线性组合函数，即BP神经网络.

1.2RVM基本原理

Tipping基于贝叶斯概念首次提出了关联向量机理论[7].RVM是一种有效的学习机器，具有良好的泛化能力和稀疏性.对于给定训练集{ui,yi}i=1,2,…,n，其中yi为主导变量，ui为辅助变量.RVM回归模型可表示为

(2)

式中：e为白噪声，符合N(0,σ2)分布；K(u,ui)为核函数；wi为权系数.

假定y满足独立分布，则整个数据集的似然函数为

(3)

式中：y=[y1,y2,…,yn]T，ψ(u)=[φ(u1),φ(u2),…,φ(un)]T，φ(ui)=1,K(u1,ui),K(u2,ui),…,K(un,ui).

为求解参数w和σ2的最优值，可用最大化似然函数直接进行估计.为保证模型的稀疏性，避免模型参数在训练过程中出现过拟合，可给权值w定义明确的先验概率分布，即

(4)

式中：α，w分别为相对应的超参数，且满足Gamma分布.

RVM的一个重要特征就是给各权值限定先决条件，在经足够次数更新，绝大多数超参数α将趋于无穷大，对应权值趋于0，与之对应的ui则称为无关变量；反之，少数稳定趋于有限值的超参数α对应的ui则称为关联向量.

结合贝叶斯公式和式(3，4)，可计算得到超参数的后验分布，即

(5)

该后验分布满足高斯独立分布，后验协方差矩阵为

Σ=(σ-2ψT(u)ψ(u)+A)-1

(6)

式中：对角矩阵A=diag(α0，α1，…，αn)；后验均值μ=σ-2ΣψT(u)y.

假定给定一个新样本集unew，则相应的输出变量概率分布服从高斯分布，相应的预测值ynew=μTψ(unew).

RVM模型的非线性问题处理能力绝大程度上由核函数决定，其直接影响到模型性能的优劣.常见的核函数有Poly核、Gauss核和Spline核，其数学表达式分别为

(7)

(8)

KSpline(ui,uj)=1+uiuj+uiujmin(ui,uj)-

(9)

式中：d为多项式级数；δ为高斯核宽.

不同核函数各具不同特性，其中Poly核函数可用于捕捉非稳态特性，能提取距待测点较远的全局信息，外推性较强；Gauss核函能准确描述稳态性质，可有效提取离测试点较近的信息，学习能力较强；Spline核作为一种可灵活分段的三次函数，能有效避免数据的过拟合[8].

1.3 鱼群算法优化BP神经网络模型参数

BP神经网络模型作为非线性组合函数，在训练过程中易陷入局部最优值，且收敛速度慢.鱼群优化算法是一种新型仿生集群智能优化算法，其通过对鱼群觅食、聚群及追尾等行为的模拟，由个体局部寻优进而实现整体的全局优化，具有较强的并行处理能力、寻优速度快、对初始值不敏感、简单易行和鲁棒性强等优点[9]，故BP神经网络的优化训练可采用鱼群优化算法来实现.

人工鱼群优化算法是一种循环迭代算法，在BP神经网络优化训练过程中以误差最小化为目标，通过不断更新初始权重和阈值，以达到最终优化目的.实施流程如下：

1)网络结构确定.BP神经网络选择3层网络结构，确定输入层神经元数R、输出层神经元数S1以及隐含层各层神经元数S2.

2)人工鱼参数设置.设定人工鱼数目f、最大迭代次数m、人工鱼感知范围v、移动步长s、拥挤度因子Δ，权重w和阈值c取值范围l.

3)确定食物浓度函数FC.以网络预测平均绝对误差的倒数作为食物浓度函数，公告牌记录每次食物浓度最大值，同时将对应人工鱼个体计入公告牌.

4)人工鱼初始化.在待优化参数上下限范围l内随机初始化人工鱼，每条人工鱼X为v维(v=RS1+S1S2+S1+S2，其中RS1为输入层和隐含层神经元的连接权数目，S1S2为隐含层阈值数目，S1为隐含层和输出层之间的连接权数目，S2为输出层阈值数目)，整个鱼群是v×f维矩阵，每次鱼群行为都是f条人工鱼并行寻优.

5)鱼群行为模拟.分别模拟鱼群追尾和聚群行为，选择行动后食物浓度值FC较大的行为执行，缺省行为为觅食行为.

(10)

式中：τ为(0，1)之间的随机数；s为移动步长.

(11)

(12)

6)公告牌.每次鱼群行为发生之后都要将当前状态与公告牌状态进行比较，若优于公告牌状态则取而代之.

7)终止条件判断.判断迭代次数g是否达到最大迭代次数，若满足，则输出最大食物浓度值及最优代优参数组合；否则g=g+1，返回步骤5)继续依次执行.

1.4 实施步骤

首先选择不同核函数建个多个RVM子模型；然后利用BP网络模拟非线性组合函数，以完成多个RVM模型的有效融合；同时，训练过程采用鱼群优化算法分别对BP神经网络的初始权重和阈值进行优化训练.该组合模型的具体步骤如图2所示.

图2 组合模型的建立流程图Fig.2 Operating flow diagram of combination model

1)将样本集划分成训练集和测试集，选择各RVM子模型的核函数，利用训练集建立各核函数的RVM子模型.

2)确定BP神经网络的训练样本，以各子模型的预测信息作为BP神经网络的输入，对应实际值作为BP神经网络的输出.

3)确定BP神经网络的拓扑结构，即网络隐含层数和各隐含层的神经元个数，同时确定BP神经网络所需的各传递函数类型.

4)利用鱼群优化算法优化选取BP神经网络的最优初始权重和阈值.

5)将最优初始权重和阈值代入BP神经网络，并利用步骤2)中的训练样本，对神经网络进行反复训练找到一个拟合效果最佳的网络结构，并保存该网络.

6)采用测试集测试非线性组合模型的模型性能，以评价模型的预测效果.

2 实例仿真

2.1MTO反再部分工艺

甲醇制烯烃(MTO)生产过程反再部分的工艺流程简图如图3所示.甲醇原料自外部进入缓冲罐，经进料泵升压，再经一系列换热器装置换热后进入反应器；在反应器内，甲醇和来自再生器的高温再生催化剂接触，并在催化剂表面快速反应；反应后积炭的待再生催化剂返回再生器，进行烧焦处理完成再生，重新进入反应器再次参与反应.

乙烯收率直接反映MTO生产工艺的效率高低，因此有必要对反应器出口处乙烯收率进行实时在线监测.以下将基于AFSA-BPNN的MRVM模型非线性融合建模方法应用于乙烯收率软测量研究中.

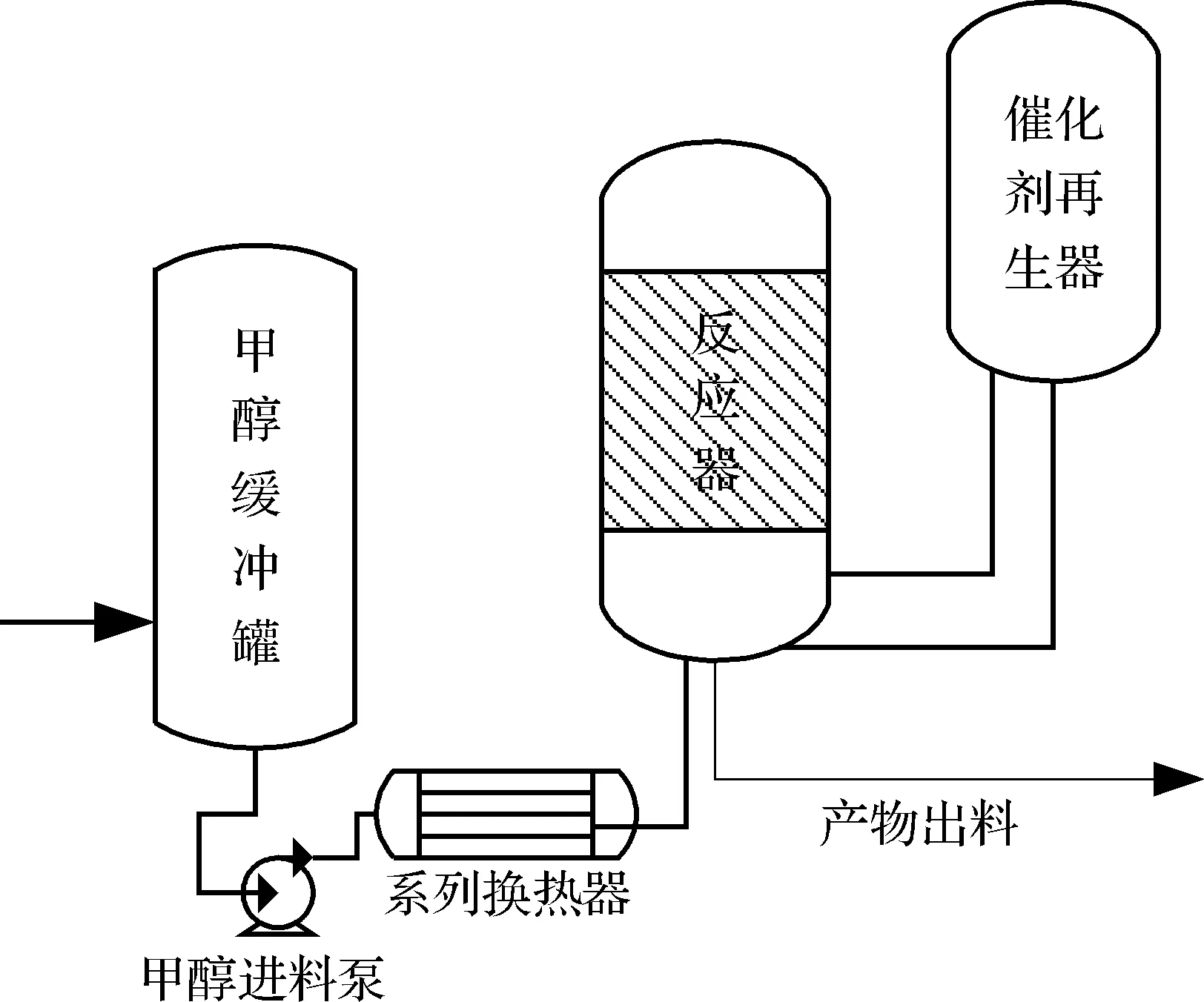
图3 MTO反再部分工艺流程简图Fig.3 Process flow sketch of MTO reaction-regeneration system

2.2 辅助变量选择与数据预处理

在认真分析MTO反应动力学和生产工艺流程的基础上，选择甲醇进料流量、甲醇进料温度、反应器压力、反应器密相段温度、催化剂在反应器中密相段藏量、再生器主风流量和再生器总藏量等作为软测量模型的辅助变量，反应器出口处乙烯收率则作为软测量模型的主导变量.

对原始样本数据集进行预处理，通过滤波方法消除样本数据随机误差，利用3σ准则删除异常数据，并进行归一化处理.经预处理后，共得到72组样本数据，选择前36组作为训练集，用于建立软测量模型；后36组作为测试集，用于测试软测量模型性能.

2.3 模型参数设置

选择Gauss核、Spline核及Poly核分别建立三个关联向量机子模型，其中高斯核宽δ=2.7，多项式级数d=3.根据研究对象的特点和组合模型的结构特点，神经网络的参数设置为：拓扑结构定为3×8×1(其中隐含层神经元数由文献[10]中的经验公式决定，此处取为8)，网络隐含层传递函数为tansig，输出层传递函数为purelin；训练函数为trainlm，学习函数为learngdm，表现函数为mse，训练次数为10 000次，训练目标为10-5.

鱼群优化算法的参数设置为：人工鱼数f=50，最大迭代次数m=100，感知范围v=0.1，移动步长s=0.05，觅食行为尝试的最大次数t=50，拥挤度因子Δ=0.618.待优化参数取值区间l=[0.000 1，1].

2.4 结果与讨论

乙烯收率与各辅助变量之间存在强非线性关系，此时若只是建立线性组合模型，其预测精度较低.但为了验证所提出建模方法的有效性，仍将线性组合模型作为对比模型.常见的线性组合方法有方差倒数法、算术平均法和最优加权法，其中最优加权组合以各子模型预测结果的组合误差平方和最小为优化准则，求解各子模型的最优加权系数来建立最优线性组合模型，所得模型预测精度较高[11].采用最优加权方法建立MRVM的线性组合模型，该线性组合模型的数学表达式为

Y=0.072 8yG+0.147 5yP+0.779 7yS

(13)

式中：yG，yP，yS分别为Gauss核、Poly核和Spline核RVM子模型的输出.

两种组合模型(线性组合和非线性组合)与三种单一RVM模型(yG，yP和yS)的预测效果分别如图4，5所示.

图4 子模型乙烯收率预测效果Fig.4 Ethylene yield prediction performance of sub-models

图5 组合模型乙烯收率预测效果Fig.5 Ethylene yield prediction performance of combination models

由图4，5可知：各单一子模型和线性组合模型均能大致跟踪实际生产过程中主导变量的变化趋势，且线性组合模型的跟踪效果要优于各子模型.但相比而言，非线性组合模型则具有更佳的预测效果，能更准确地跟踪实际生产过程中主导变量的变化趋势.

为了定量比较各模型的预测性能，采用均方根误差(RMSE)、平均相对误差(MRE)和平均绝对误差(MAE)作为模型的预测性能指标，各性能指标的具体计算公式为

(14)

(15)

(16)

两种组合模型与三种单一RVM模型的性能指标如表1所示.由表1可知：线性组合模型的性能指标要优于单一RVM模型，而非线性组合模型的性能指标又要优于线性组合模型，其三项性能指标分别达到0.013 5，0.135 3和0.065 5，与其余四种模型的性能指标数值相比，至少下降了40%，由此表明非线性组合模型具有较佳的预测精度.

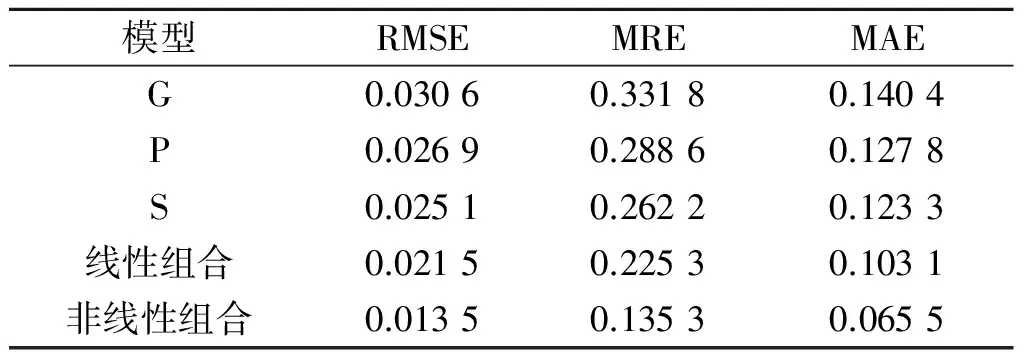
表1 误差效果对比分析

具有不同核函数的RVM子模型可对样本数据的不同特征信息进行区分，子模型的预测信息可视为不同信息片段.通过BP神经网络集成分散单个模型特有的不确定性，使得各模型之间在性能上得到了互补，全面体现出样本数据的各维特性，降低了总体的不确定性，从而提高了模型的预测精度.另外，BP神经网络具有强非线性学习能力，采用BP神经网络实现多模型融合，可使组合模型更好地满足非线性对象的建模需求.因此，基于AFSA-BPNN的MRVM模型非线性融合建模方法能用于建立具有较佳预测精度的软测量模型，非常适用于非线性化工对象的软测量建模研究中.

3 结 论

在RVM软测量模型的研究工作基础上，针对实际工况的强非线性问题，提出了一种基于AFSA-BPNN的MRVM模型非线性融合建模方法，利用BP神经网络实现了不同关联向量机子模型输出信息的有效非线性融合，并通过鱼群优化算法快速、高效地完成BP神经网络初始权值和阈值的参数寻优，成功克服了传统BP神经网络所存在的收敛较慢、易收敛于局部最优等不足.由甲醇制烯烃生产过程乙烯收率软测量的研究结果表明：采用基于AFSA-BPNN的MRVM非线性组合建模方法建立的软测量模型，既实现了准确预测乙烯收率的目的，又为其他化工过程的软测量应用研究提供了一种性能较好的建模方法.

[1] 王卫红,卓鹏宇.基于PCA-FOA-SVR的股票价格预测研究[J].浙江工业大学学报,2016,44(4):399-404.

[2] 孙明轩,余轩峰,孔颖.终态神经计算:有限时间收敛性与相关应用[J].浙江工业大学学报,2015,43(3):311-317.

[3] 曾甜玲,温志渝,温中泉.相关向量机在污水硝氮检测中的应用[J].光谱学与光谱分析,2013,33(4):1048-1051.

[4] 李丽娜,马俊,梁德骕,等.基于相关向量机及模拟退火的损耗模型训练[J].计算机工程与设计,2016,37(1):139-145.

[5] CLEMENTS M P, HARVEY D I. Combining probability forecasts[J]. International journal of forecasting,2011,27(2):208-223.

[6] 孟凡丽,郑棋,李燕,等.基于BP神经网络的深基坑围护变形预测[J].浙江工业大学学报,2014,42(4):367-372.

[7] TIPPING M E. Sparse bayesian learning and relevance vector machine[J]. Journal of machine learning research,2001,35(3):211-244.

[8] ALAMANIOTIS M, BARGIOTAS D, BOURBAKIS N G, et al. Genetic optimal regression of relevance vector machines for electricity pricing signal forecasting in smart grids[J]. IEEE transactions on smart grid,2015,51(12):2997-3005.

[9] 李晓磊.一种新型的智能优化算法-人工鱼群算法[D].杭州:浙江大学,2003.

[10] 丁硕,巫庆辉.基于改进BP神经网络的函数逼近性能对比研究[J].计算机与现代化,2012(11):10-13.

[11] 赵玲,许宏科,程鸿亮.基于最优加权组合模型的道路交通事故预测[J].计算机工程与应用,2013,49(24):11-15.

(责任编辑：刘 岩)

Nonlinear fusion modeling of MRVM model based on AFSA-BPNN

XIA Luyue1,2, LIU Yong1,2, PAN Haitian1,2

(1.College of Chemical Engineering, Zhejiang University of Technology, Hangzhou 310014, China; 2.Zhejiang Province Key Laboratory of Biofuel, Hangzhou 310014, China)

Aiming at the nonlinearity and multiple operating modes features of chemical process, a modeling method based on MRVM nonlinearly integrated by BPNN was proposed. Firstly, several RVM sub-models with the different kernel function were developed. Then predictive information of sub-models was combined by BPNN, and the initial weight and threshold were optimized by AFSA. Finally, the nonlinear fusion modeling of MRVM was developed. The modeling method was applied to develop a soft sensor of ethylene yield in the MTO production. The results indicated that the soft sensor based on the modeling method had better prediction precision than single RVM model and optimum weighted combination model.

MRVM; BPNN; AFSA; combined model; nonlinearity

2016-11-01

国家自然科学基金资助项目(21676251)

夏陆岳(1979—)，男，浙江永康人，讲师，研究方向为化工过程建模与优化，E-mail：lyxia@zjut.edu.cn.

TP391

A

1006-4303(2017)03-0294-06