变截面井筒式地下连续墙竖向承载力计算研究

文 华，李梦妮，邹娇丽，吴九江，程谦恭

(1.西南科技大学 土木工程与建筑学院，四川 绵阳 621010；2.西南交通大学 地球科学与环境工程学院，四川 成都 610031)

变截面井筒式地下连续墙竖向承载力计算研究

文 华1，李梦妮1，邹娇丽1，吴九江1，程谦恭2

(1.西南科技大学 土木工程与建筑学院，四川 绵阳 621010；2.西南交通大学 地球科学与环境工程学院，四川 成都 610031)

根据变截面井筒式地下连续墙的荷载传递特性及传递机理，借鉴和参考目前已有的桩基础和地下连续墙基础的承载力计算方法和现有的一些研究结果，通过理论分析，提出适合于变截面井筒式地下连续墙的竖向承载力的计算方法.建立了4个不同闭合段墙高，相同开放段墙宽的变截面井筒式地下连续墙模型和5个不同开放段墙宽，相同闭合段墙高的变截面井筒式地下连续墙模型，通过模型的计算结果和数值模拟结果的对比，确定了计算方法中的安全系数取值为K1=1.8，K2=2.5.

井筒式地下连续墙；变截面井筒式地下连续墙；竖向承载力计算

地下连续墙基础作为一种新型的桥梁基础，具有良好的工程特性，在国内应用的工程实例极少，就国外而言，地下连续墙作为大跨度桥梁深基础的工程实例已有不少，尤其得到了日本工程界的高度重视和开发应用，其中“井筒式地下连续墙”[1](Caisson-typediaphragmwall)与“多壁基础”[2](Multi-wallfoundation)是采用较多的两种基础形式，已在大量的城市高架、铁道与跨海桥梁的基础结构中取得了应用.但是井筒式地下连续墙桥梁基础对施工机械和施工工艺要求较高，施工成本比桩基础高，而多壁式基础的整体性较之井筒式地下连续墙偏弱，这就限制了地下连续墙桥梁基础应用.作为新型地下连续墙基础，变截面井筒式地下连续墙基础，吸收了大量采用的井筒式和多壁式地下连续墙桥梁基础的优点.变截面井筒式地下连续墙在基础上部采用的是与井筒式地下连续墙相同结构形式，即用刚性接头连接相邻的地下连续墙墙体，在形成的闭合矩形框架上面设置顶板(承台)[3]；在基础下部，采用了与多壁基础相同的复壁式板桩结构，并与上部刚性连接.从上往下观察，基础的截面形式由闭合的地下连续墙转变为开放式的多段墙，但整体仍为井筒式结构，故称其为变截面井筒式地下连续墙基础.与多壁基础相比，由于上部刚性闭合墙体的存在，变截面井筒式地下连续墙基础整体的刚度增加，其抵抗水平荷载及抗震能力获得有效提升；与井筒式地下连续墙比较，由于下部采用了非闭合的壁板桩结构，变截面井筒式地下连续墙基础下部土芯不再是四周封闭的“土柱”[3]，墙内摩阻力会得到极大提升，同时基础的“群墙效应”[2]将大幅降低，这必然使得相同截面尺寸条件下，变截面井筒式地下连续墙的承载力将与井筒式地下连续墙基础相差不大.

近年来，国内外学者对井筒式地下连续墙竖向承载性能做了大量研究，主要集中在荷载传递机理和竖向承载力组成方面[4-5].在地下连续墙的计算方法方面，孙学先[6]在国内率先开展了研究，其他学者也提出了一些地下连续墙竖向承载力简化计算公式[7-8].变截面井筒式地下连续墙具有极高的工程应用前景，但由于目前国内外无相关的文献进行报道，尚处于研究的初步阶段，其承载特性与设计计算方法急需研究与解决.

1 变截面井筒式地下连续墙竖向承载力计算方法

1.1 桩与地下连续墙竖向承载力计算方法

由于目前没有变截面井筒式地下连续墙竖向承载力计算方法的研究，选择有关桩[9-11]和已有的地下连续墙的文献作为参考.

1)JGJ94—2008《建筑桩基技术规范》[12]中关于桩基础设计承载力的经验参数法具有较好的参考价值.可根据土的物理指标与承载力参数之间的经验关系，确定单桩竖向极限承载力标准值，即

Quk=Qsk+Qpk=u∑qsikli+qpkAp

(1)

式中：Qsk为桩的极限侧摩阻力；Qpk为桩的极限端阻力；u为桩的周长；qsik为桩侧第i层土的极限侧摩阻力标准值；li为第i层土的计算长度；qpk为极限端阻力标准值；Ap为桩的截面积.qsik，qpk可按实测数据或参考规范推荐数据[12]取值.

2) 《岩土工程勘察设计手册》[13]就预估单桩承载力进行估算，即

(2)

式中：Rk为单桩承载力标准值；K为安全系数，一般取2；up为桩身周边长度；qsti为第i层土的桩周极限摩阻力；Li为按土层划分的各段桩长；qpti为桩端土的极限端阻力；Ap为桩身横截面面积.

3)侯永茂[8]在研究格形地下连续墙(即一系列地下连续墙槽段而成的格形结构)的竖向承载特性时，提出了在初步设计时，其竖向极限承载力标准值可估算为

Quk=uc∑qsikli+ηqwkAst+qwkAwl+0.94qwkAwt

(3)

式中：Quk为格形地下连续墙竖向极限承载力标准值；uc为格形地下连续墙外侧周长；qsik为墙侧第i层土的极限侧摩阻力标准值；li为第i层土的厚度；η为墙芯土体端应力系数；qwk为极限端阻力标准值；Ast为格形地下连续墙强心土体截面面积；Awl为纵墙截面面积；Awt为隔墙截面面积.

4)程谦恭等[14]对闭合地下连续墙的承载力计算进行了深入的研究，提出了闭合墙的容许承载力ppa的计算，其公式为

(4)

式中：ppa为闭合墙基础容许承载力；Qsw为外侧中性点以下土体总极限正摩阻力；Qsn为内侧总极限正摩阻力；Qn为总极限负摩阻力；Qp为总极限负摩阻力；K1,K2分别为分项安全系数.

式(1，2)分别适用于单桩竖向极限承载力标准值和单桩承载力标准值计算.桩基础的相关规范和计算方法为同为深基础的地下连续墙的计算提供了参考，但是由于地下连续墙的基础形式与桩基础存在差异，变截面井筒式地下连续墙的承载力计算不能照搬桩基础的方法.式(3，4)适用于单室和格形井筒式地下连续墙计算，已有的单室和格形地下连续墙的结构形式与变截面井筒式地下连续墙更为相似，能为变截面井筒式地下连续墙的计算提供更为有效的参考，但由于变截面井筒式地下连续墙结构形式与单室和格式地下连续墙仍存在差异，必须结合变截面井筒式地下连续墙的结构构造，提出更有针对性的计算方法.

1.2 变截面井筒式地下连续墙竖向承载力计算方法

变截面井筒式地下连续墙在基础上部H1段采用的是与井筒式地下连续墙相同结构形式，在基础下部H2段，采用了与多壁基础相同的复壁式板桩结构，并与上部H1段刚性连接，变截面井筒式地下连续墙示意图如图1所示.

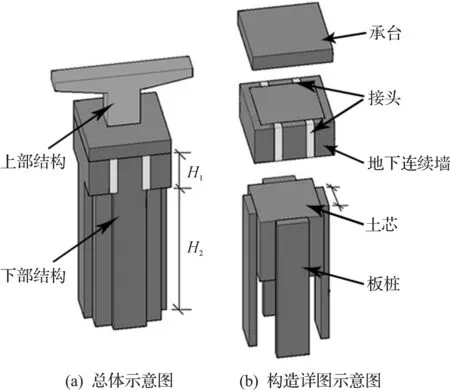
图1 变截面井筒式地下连续墙示意图Fig. 1 The caisson diaphragm wall with variable cross-section

经分析可知：变截面井筒式地下连续墙的竖向承载力Quk由外摩阻力Qsw、闭合段内摩阻力Qsnb、闭合段内摩阻力Qsnk、侧边摩阻力Qsc、闭合段墙端阻力Qpb、开放段墙端阻力Qpk和承台土反力Qc组成，见图2变截面井筒式地下连续墙竖向承载力计算示意图.但变截面井筒式地下连续墙的荷载传递较为复杂，外摩阻力、内摩阻力和端阻力等并不同时发挥，且根据本文中基础极限荷载的确定方法，变截面井筒式地下连续墙在达到极限荷载时，摩阻力和端阻力均未达到极限状态.结合对桩和地下连续墙基础承载力的计算方法，加入安全系数K1,K2，给出了在初步设计时，预估变截面井筒式地下连续墙的承载力计算公式为

(5)

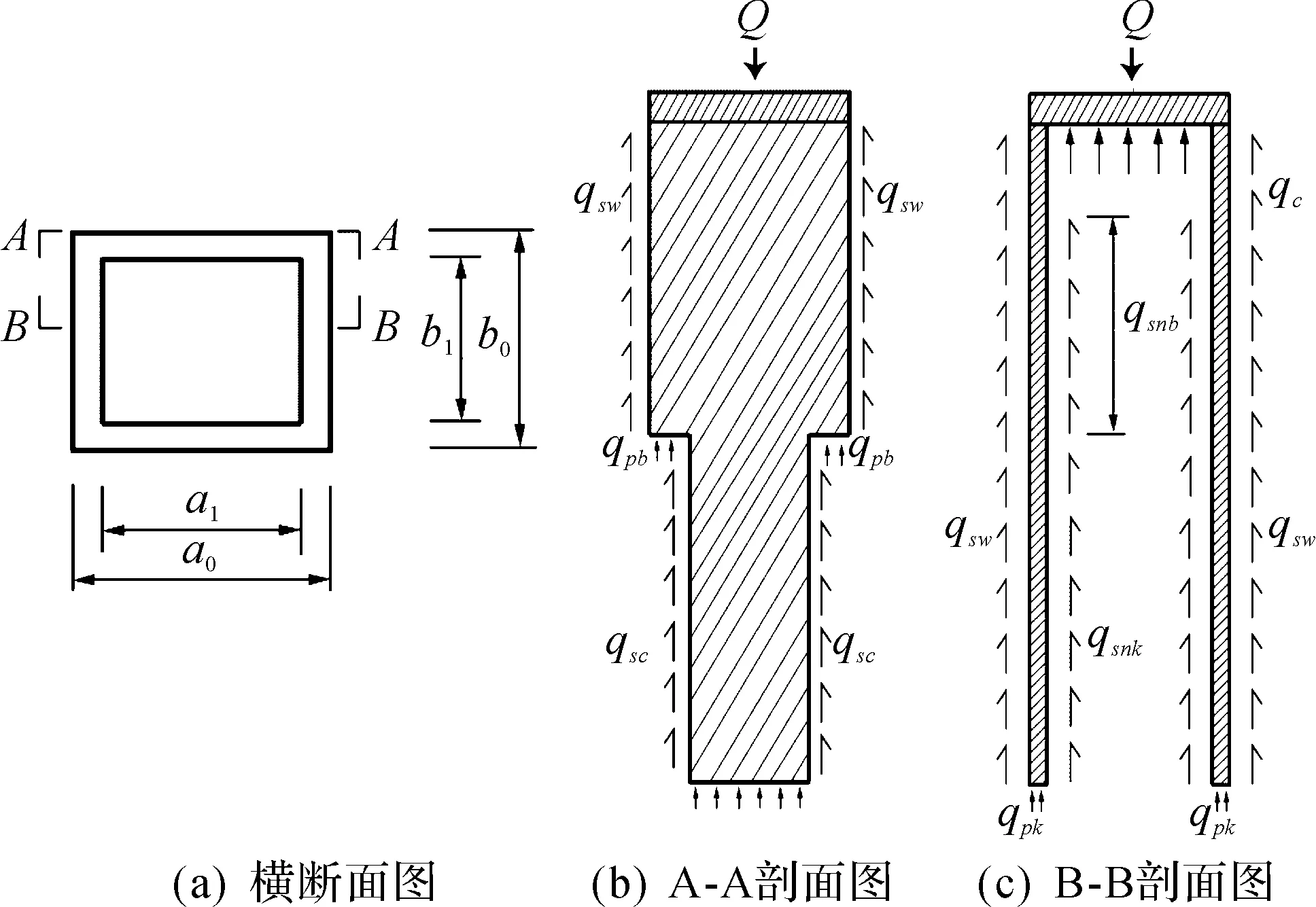
图2 变截面井筒式地下连续墙竖向承载力计算示意图Fig.2 Diagram of vertical bearing capacity of the caisson-type diaphragm wall with variable cross-section

1.2.1 外摩阻力的计算

根据前面的数值模拟分析的外摩阻力分布规律，变截面井筒式地下连续墙外摩阻力可参考桩基侧摩阻力公式进行近似计算，即

Qsw=uw∑qswili

(6)

式中：uw为墙体外侧周长；qswi为墙顶以下第i层土的极限侧摩阻力标准值，若无当地经验值时，可参照文献[12]进行选取；li为墙顶以下第i层土的厚度.

1.2.2 内摩阻力的计算

变截面井筒式地下连续墙内摩阻力的发挥发展性状相当复杂，闭合段内摩阻力的发挥受到了闭合段墙体的限制，发挥性状与井筒式地下连续墙内摩阻力的发挥相似，因此参考日本学者的有关研究成果[12-13]，闭合段内摩阻力建议进行近似计算，即

Qsnb=un∑qsnjlj

(7)

式中：un为墙体内侧周长；qsnj为闭合段墙端以上第j层土的极限侧摩阻力标准值，若无当地经验值时，可参照文献[12]进行选取；lj为计算长度.

日本学者平井正哉和田坂幹雄等[15-16]认为，闭合型的地下连续墙内摩阻力的发挥主要集中在闭合墙的墙端附近，可以近似地从墙端往上发挥了内摩阻力的墙段长度lj来计算闭合墙的内摩阻力.根据日本学者的研究，lj取值为

lj=min(a1,b1)=b1=b0-2t0

(8)

式中：a1为墙体内侧长边长；b1为墙体内侧短边长；b0为墙体外侧短边长；t0为墙体厚度.

综合分析，开放段内侧未受到封闭的“土芯”的限制，其发挥性状靠近外摩阻力的发挥，因此，开放段内摩阻力计算参照外摩阻力的计算方式，其近似计算建议为

Qsnk=4B∑qsnklk

(9)

式中：B为开放段墙体宽度；qsnk为开放段墙端以上第k层土的极限侧摩阻力标准值，若无当地经验值时，可参照文献[12]进行选取；lk为开放段墙端以上第k层土的厚度.

1.2.3 侧边摩阻力的计算

开放段侧边摩阻力的发挥性状同外摩阻力相似，即

Qsc=8t0∑qscmlm

(10)

式中：t0为墙体厚度；qscm为闭合段墙端以下第m层土的极限摩阻力标准值，若无当地经验值时，可参照文献[12]进行选取；lm闭合段墙端以下第m层土的厚度.

1.2.4 闭合段墙端阻力的计算

闭合段墙端阻力的计算公式为

Qpb=qpbApb

(11)

(12)

式中：qpb为极限端阻力标准值，若无当地经验值时，可参照文献[12]进行选取；Apb为闭合段墙端面积，按式(12)计算；B为开放段墙体宽度.

1.2.5 开放段墙端阻力的计算

开放段墙端阻力的计算式为

Qpk=qpkApk

(13)

Apk=4Bt0

(14)

式中：qpk为开放段极限端阻力标准值，若无当地经验值时，可参照文献[12]；Apk为开放段墙端面积，可按式(14)计算；B为开放段墙体宽度.

1.2.6 承台土反力的计算

在变截面井筒式地下连续墙中，由于墙体的四面包围，土芯成为了一个封闭的“土柱”，且墙体整体性好，刚度大，因此承台土反力的发挥非常有限，承台土反力的荷载分担比非常的小，对竖向荷载的承担贡献很小.因此，在变截面井筒式地下连续墙的竖向承载力的计算中，近似的认为承台土反力为0.这种保守的处理的方法是偏安全的.

1.2.7 安全系数K1,K2的选取

因为地下连续墙和桩基础一样，端阻力都是最后才发挥的，因此K2>K1，结合《岩土工程勘察设计手册》[16]中的安全系数取法：K1为1.5～2，K2为2～3.因此，变截面井筒式地下连续墙作为一种新型的竖向承载基础，在初步设计时，对其竖向承载力进行估算，即

(15)

式中各符号含义同前文.

2 变截面井筒式地下连续墙竖向承载力算例分析

首先建立FLAC3D数值模型，通过对变截面井筒式地下连续墙进行数值仿真实验考查不同深度处土体对基础的力学指标，比如极限侧摩阻力标准值qpb、闭合段极限端阻力标准值和开放段极限端阻力标准值qpk.

再根据算例中土层的参数以及上述对变截面井筒式地下连续墙竖向承载力的近似方法计算，选取安全系数K1,K2的不同组合，将不同的安全系数K1,K2组合下的竖向承载力近似方法计算结果与数值模拟结果进行对比.初步确定变截面井筒式地下连续墙的竖向承载力近似计算方法中的安全系数的取值范围.

2.1 变截面井筒式地下连续墙数值模拟

通过FLAC3D有限差分程序建立了4个不同闭合段墙高，相同开放段墙宽的变截面井筒式地下连续墙模型和5个不同开放段墙宽，相同闭合段墙高的变截面井筒式地下连续墙模型，变截面井筒式地下连续墙数值模型如图3所示，变截面井筒式地下连续墙模型参数如表1所示.

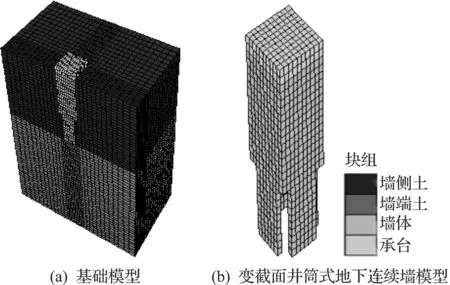
图3 变截面井筒式地下连续墙数值模型Fig.3 Caisson diaphragm wall with variable cross-section numerical model

2.1.1 本构模型

本次数值模拟中，变截面井筒式地下连续墙的墙身都采用线弹性本构模型，模型土体采用摩尔-库伦本构模型.

2.1.2 基本算例计算参数

由于变截面井筒式地下连续墙基础还未见报道，没有实际的工程进行参考，主要计算参数的选取主要参考现有地下连续墙基础[17-18]和经验数据.墙体与承台的混凝土强度取C25，墙体、承台、墙测土和墙端土的计算参数选取结果如表2所示.

表1 变截面井筒式地下连续墙模型参数

表2 基本计算参数表

2.1.3 接触面单元参数

结合吴九江等[18-19]对接触面单元模型土体的法向刚度kn，则取kn=100ks，切向刚度ks取墙侧土体的剪切模量值.

根据前人研究经验，接触界面黏聚力cc和接触界面摩擦角φc通常由现场或室内直剪摩擦试验确定.参考Acer等[20]已针对接触面摩擦进行了大量的直剪试验表明：对于黏性土，取φc/φ为0.6～0.7是比较合理的；对界面黏聚力cc可取墙周土体的黏聚力的2/3；对于界面摩擦角φc可取墙周土体内摩擦角的2/3，具体接触面单元计算参数如表3所示.

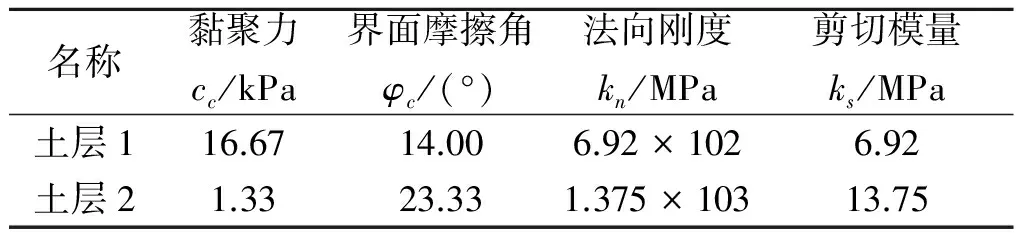
表3 接触面单元计算参数表

2.1.4 计算区域

井筒式地下连续墙基础从结构形式上来看，与筒型基础在结构型式上有些接近，杜杰等[21]对井筒式地下连续墙基础的水平计算区域取墙外侧距离水平计算边界为3a0，a0取基础形式长边值.孟凡超等[22]采用三维有限元数值模拟软件对黄土地层中的闭合墙基础的沉降特性进行了分析，结果表明整个模型基础沉降的主要部分是墙端下约1.5倍基础宽度范围内的土体的竖向变形.

鉴于上述研究成果，对基本模型汇总的变截面井筒式地下连续墙基础的竖向计算区域取为：竖向计算边界为2.5L(L为地下连续墙的埋深)，即62.5 m；水平向为7a0(a0为地下连续墙外边长直径).

2.1.5 加载方式

关于井筒式地下连续墙基础的容许承载力计算方法[14]，参考JGJ 94—2008《建筑桩基技术规范》[12]中桩基极限侧阻力标准值和极限端阻力标准值，预估井筒式地下连续墙的容许承载力为52 MN.

根据JTG/TF 50—2011《公路桥涵施工技术规范》[23]，按照基础静载试验分15级施加上部荷载，第一级荷载为8 MN，其后每级荷载均以5 MN进行叠加，共加载至预估荷载的150%.

2.1.6 基础竖向极限承载力的确定标准

关于地下连续墙作为基础的竖向承载力的确定方法，目前我国还没有可参考的国家标准或者行业标准.因此，参照JGJ 94—2008《建筑桩基技术规范》[12]确定地下连续墙的竖向极限承载力：在相同极限荷载作用下，后一级荷载引起的沉降量5倍于前一级荷载的引起的沉降量时荷载—沉降曲线会出现陡降段，此时根据荷载—沉降曲线的变化特征，取前一级荷载作为极限承载力；对于荷载—沉降曲线呈缓变型的，根据沉降量取墙顶沉降量超过60 mm时所对应的墙顶荷载作为极限承载力；当不符合前两种情况时，若墙顶荷载达到墙身材料强度，则墙顶荷载为地下连续墙的极限荷载.

2.2 变截面井筒式地下连续墙竖向承载力近似方法

通过变截面井筒式地下连续墙数值仿真实验结果选取极限侧摩阻力标准值为55 kPa，闭合段极限端阻力标准值qpb=1 000 kPa，开放段极限端阻力标准值qpk=1 800 kPa，其他计算参数选取见2.1小节.按照1.2节变截面井筒式地下连续墙竖向承载力近似计算方法进行计算，初步确定安全系数K1，K2的取值范围，选取三组安全系数的组合，分别为：第一组K1=1.5，K2=2；第二组K1=1.8，K2=2.5；第三组K1=2，K2=3，具体极限竖向承载力近似方法计算结果与数值模拟计算结果对比情况分别如表4所示.

表4 极限荷载近似方法计算与数值计算结果对比

由表4可知：K1，K2的取值越小，变截面井筒式地下连续墙的竖向承载力的近似方法计算结果与数值计算结果的比值越小，且K1=1.8左右，K2=2.5左右时，其变截面井筒式地下连续墙的竖向承载力的近似方法计算结果与数值计算结果较为接近.因此，推荐安全系数的取值在K1=1.8左右，K2=2.5左右.

3 结 论

参考桩和单室、格形井筒式地下连续墙的竖向承载力计算，结合变截面井筒式地下连续墙的结构构造和荷载传递机理，分析了外摩阻力、闭合段内摩阻力、开放段内摩阻力、侧边摩阻力、闭合段端阻力、开放段端阻力和承台土反力的计算方法，提出了适合于变截面井筒式地下连续墙的竖向承载力计算方法，并且将竖向承载力计算方法与前述数值模拟结果相对比，经过多组试算对比分析，确定变截面井筒式地下连续墙的竖向承载力近似计算方法中的安全系数的取值为K1=1.8，K2=2.5.由于目前还未开展变截面井筒式地下连续墙基础的现场试验研究且尚无工程应用，因此本方法还有待后续试验和工程实践的进一步验证和改进.

[1] 海野隆哉，大植英亮.地下連続壁の井筒設計法と現場水平載荷試驗[J].土木技術,1980,36(5)：48-57.

[2] 文华,程谦恭,陈晓东,等．竖向荷载下矩形闭合地下连续墙桥梁基础群墙效应研究[J].岩土力学,2009(1):152-156.

[3] 文华,程谦恭,宋章.矩形闭合墙桥梁基础墙-土-承台相互作用研究[J].土木工程学报,2007,40(8)：67-73.

[4] 吴九江,程谦恭,文华,等.格栅式地下连续墙竖向载荷模型试验研究[J].岩石力学与工程学报,2015(12):2580-2592.

[5] 吴九江,文华,程谦恭,等.基于接触面参数反演的格栅式地下连续墙桥梁基础竖向承载特性数值分析[J].岩土工程学报,2016,38(8):1-10.

[6] 孙学先,崔文鉴.地下地下连续墙基础的计算方法研究[J].兰州铁道学院学报,1991,10(2):60-69.

[7] 戴国亮,龚维明,周香琴，等.单室井筒式地下连续墙水平承载力试验与计算方法研究[J].建筑结构学报,2012，33(9):67-73.

[8] 侯永茂.格形地下连续墙竖向承载特性研究[J].岩土工程学报,2012,34(4)：701-708.

[9] 卢成原,黄瑜明.不同土质中支盘桩基础合理盘距和桩距研究[J].浙江工业大学学报,2015,43(2):232-236.

[10] 卢成原,朱晨泽,汪金勇.支盘桩盘体形状对承载性状影响的研究[J].浙江工业大学,2015,43(3):279-282.

[11] 卢成原,李汉杰.支盘桩群桩抗拔承载性状试验研究[J].浙江工业大学学报,2014,42(3):298-301.

[12] 中华人民共和国行业标准.桩基技术规范：JGJ94—2008[S].北京:中国建筑工业出版社,2008.

[13] 林宗元.岩土工程勘察设计手册[M].沈阳：辽宁科学技术出版社,1996.

[14] 程谦恭，文华，宋章.地下连续墙桥梁基础承载机理[M].北京：科学出版社，2011.

[15] 平井正哉.地中連続壁の設計と施工[J].基礎工,1997,25(2)：57-63.

[16] 田坂幹雄.地中連続壁基礎の設計事例[J].基礎工,1999,27(2)：55-59.

[17] 何明晋.格栅式地下连续墙桥梁基础沉降特性研究[D].绵阳:西南科技大学,2013.

[18] 吴九江.软土地基中格栅式地下连续墙桥梁基础竖向承载性状研究[D].成都：西南交通大学,2015.

[19] 文华.湿陷性黄土地基中矩形闭合型地下连续墙桥梁基础负摩阻力作用机理研究[D].成都：西南交通大学，2008:48.

[20]ACERYB,DURGUNOGLUHT,YUMAYMT.Interfacepropertiesofsands[J].Journalofsoilmechanicsandfoundationsdivision,ASCE,1982,108(4):648-654.

[21] 杜杰，丁红岩，刘建辉，等.筒型基础有限元分析的土体边界选取研究[J].海洋技术，2005，24(2):109-113.

[22] 孟凡超,陈晓东,舒中潘.地下连续墙基础沉降数值分析[J].公路,2007(3):55-58.

[23] 中华人民共和国行业标准.公路桥涵施工技术规范:JTG/TF50—2011[S].北京:人民交通出版社,2011.

(责任编辑：刘 岩)

Claculation of the vertical bearing capacity of caisson diaphragm walls with a variable cross-section

WEN Hua1, LI Mengni1, ZOU Jiaoli1, WU Jiujiang1, CHENG Qiangong2

(1.College of Civil Engineering and Architecture, Southwest University of Science and Technology, Mianyang 621010, China; 2. Department of Geological Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Based on the existing methods for calculating the ultimate bearing capacity of pile foundations and caisson diaphragm walls and other existing research results, a calculation method for the vertical bearing capacity of caisson diaphragm walls with a variable cross-section is presented from the theoretical analysis of the load transfer characteristics and mechanism of caisson diaphragm walls with a variable cross-section. A model of four different closure periods of high walls and five different wide open sections about caisson diaphragm walls with a variable cross-section is established and the factor of safety in the calculation method is determined asK1=1.8 andK2=2.5 by comparing the calculation results with the results of the numerical modeling.

caisson diaphragm wall; caisson diaphragm wall with a variable cross-section; bearing capacity calculation

2016-11-30

国家自然科学基金资助项目(51108393，41372292)；四川省教育厅重点科研项目(16ZA0139)

文 华(1978—)，男，湖南宜章人，教授，博士，主要从事岩土工程以及道路工程研究，E-mail：wenhua189@qq.com.

TU458

A

1006-4303(2017)03-0243-06