基于核心素养的“向心加速度”探究式教学设计

潘 通

(南京师范大学附属中学，江苏 南京 210003)



基于核心素养的“向心加速度”探究式教学设计

潘 通

(南京师范大学附属中学，江苏 南京 210003)

物理核心素养是中国学生发展核心素养的重要组成部分,物理学科教学是融入物理核心素养教育的关键途径,通过对普通高中物理课标教材中能够彰显核心物理思想与方法的关键章节进行严谨科学的教学设计是达成物理核心素养教育的有效手段.本文以普通高中课标教材人教版必修2中“向心加速度”一节为例开展探究式教学设计,力求达成融入物理核心素养的课堂教学．

核心素养;向心加速度;探究;教学设计

物理核心素养是新高中物理课程标准修订时提出的新概念,它指出物理学科教育应培养适应学生个人终身发展的必备品格和关键能力.物理核心素养主要由“物理观念”、“科学思维”、“科学探究”、“科学态度与责任”4个方面的要素构成,是课程三维目标的提炼与升华.广大一线教师在日常教学中应通过合理设计教学流程,努力达成必备品格的培养与关键能力的提升,实现物理学科的育人价值.高中物理新课标教材必修2“向心加速度”一节融合了矢量运算、极限法、小量近似等经典数理方法与思想,是锻炼学生思维的经典教学内容,值得深入研究,笔者在“2016年江苏省第四届名师论坛”活动中执教了“向心加速度”一节示范课,现将探究式教学流程展示如下．

1 导入:基于最近发展区,科学设问,激发学生探究欲望

教师:描述匀速圆周运动的物理量有哪些?

学生:线速度v； 角速度ω； 周期T； 半径r.

教师:匀速圆周运动有无加速度?

学生:有.

教师:为什么有加速度?

学生:线速度大小不变但方向时刻变化．

教师:研究匀速圆周运动加速度的大小与方向,有哪些方法?

学生:可以通过分析力来研究．

教师:请详细说明研究过程．

学生:根据牛顿第二定律,合力的方向就是加速度方向,合力大小除以质量得到加速度大小．

观察实验1: 用绳子系着的小球在较光滑的水平板上做匀速圆周运动.

教师:忽略阻力,分析小球受力．

学生:重力、支持力、绳子拉力．

教师:合力是什么?方向如何?

学生:绳子拉力,方向沿绳子指向圆心．

教师:小球加速度方向如何?大小怎样求?

学生:指向圆心,绳子拉力除以小球质量．

观察实验2: 用绳子系着的小球悬空且在水平面内做匀速圆周运动(圆锥摆).

教师:小球依然在水平面内做匀速圆周运动,小球的加速度方向如何?

学生1:沿着绳子的方向．

学生2:指向圆轨道的圆心方向．

学生3:无法确定合力的方向,所以无法确定加速度方向．

教师总结: (1) 运用牛顿第二定律研究匀速圆周运动的加速度的大小与方向确实是一种方法,但物体的受力情况往往决定于具体的运动情境,分析起来较为困难; (2) 基于研究的严谨性,每一个匀速圆周运动加速度的研究都要进行具体的受力分析,极为繁琐．

教师:有没有更好的方法呢?

学生:可以根据加速度的定义来研究．

教师:加速度如何定义?

学生:速度的变化量除以变化所需时间．

教师:速度变化量是标量还是矢量?如何确定加速度方向?

学生:速度变化量是矢量,加速度方向与速度变化量方向相同．

2 探究:基于物理学核心思想与方法,强调过程的严谨性与逻辑性,引导学生合作探究

教师:如表1所示,物体做直线运动,初速度为v1,末速度为v2,如何用矢量图表示速度变化量?

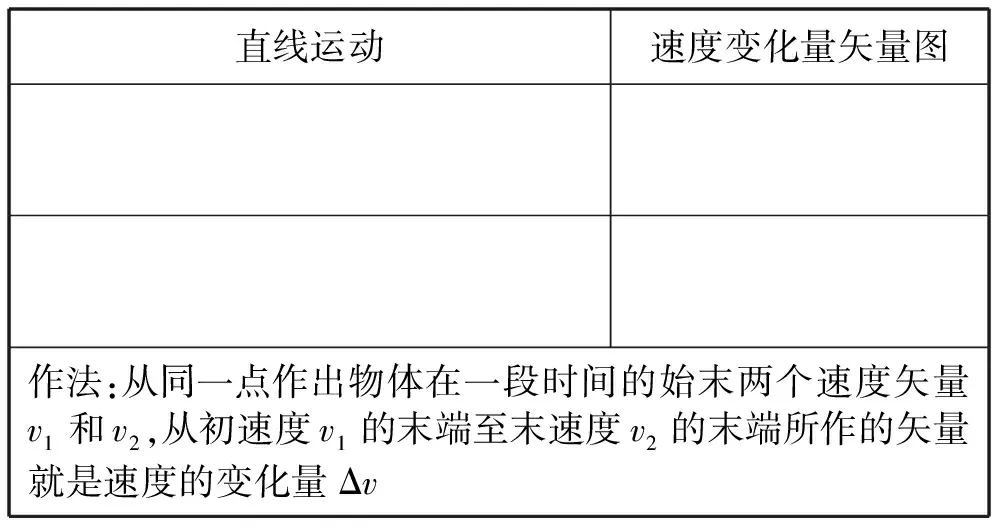
表1

教师:如表2所示,物体做曲线运动,初速度为v1,末速度为v2,如何用矢量图表示速度变化量?

表2

教师:匀速圆周运动也是曲线运动,速度变化量矢量图的作法与上面相同,如表3所示，物体做匀速圆周运动,在tA-tA+Δt时间内,由A点运动到B点,按照以上方法我们可以做出速度变化量的矢量图,其中矢量线段的长度表示速度变化量大小,箭头方向代表其方向,按照加速度定义,其与时间的比值表示加速度,能否认为这样得到的加速度就是tA时刻的加速度?

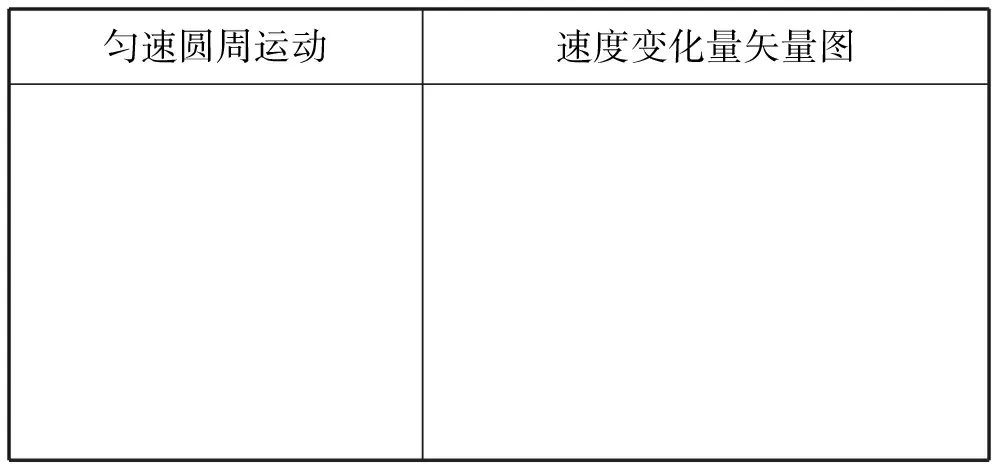
表3

学生:不能.

教师:为什么?

学生:这个加速度是tA-tA+Δt时间内的平均加速度，不是tA时刻的瞬时加速度.

教师:瞬时加速度与平均加速度哪个更能精确描述匀速圆周运动?

学生:瞬时加速度．

教师:要想得到tA时刻的瞬时加速度,应该怎样做?

学生:将Δt取短一些,用该段时间内的平均加速度代替tA时刻的瞬时加速度.

教师:若匀速圆周运动周期为T,半径为r,线速度为v,Δt取值如表4所示,同桌两人为一组,选取一个Δt取值并计算出对应的速度的变化量和加速度(已知量为r、v)．

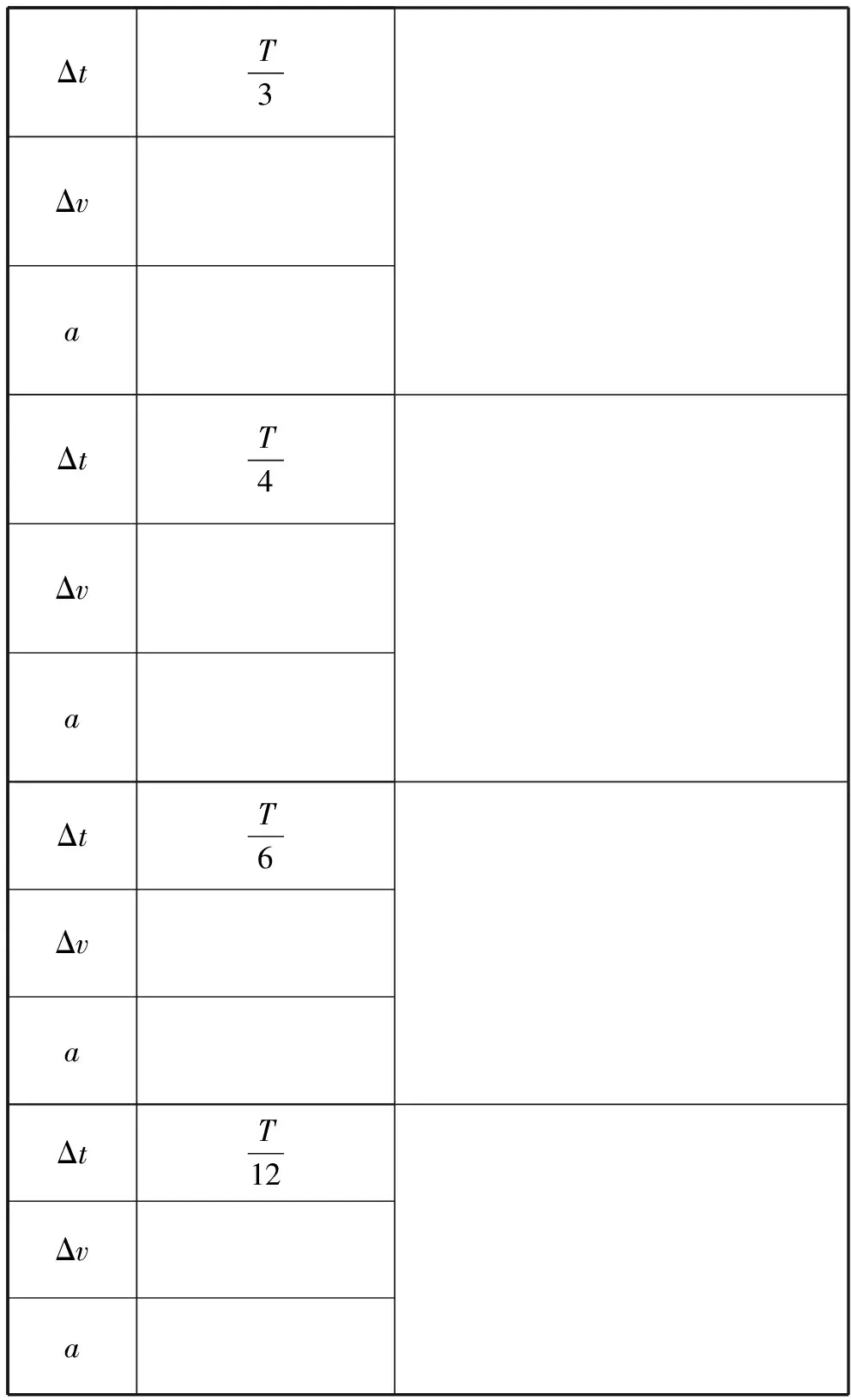
表4

教师:请每个组学生代表将计算结果填写在表5中．

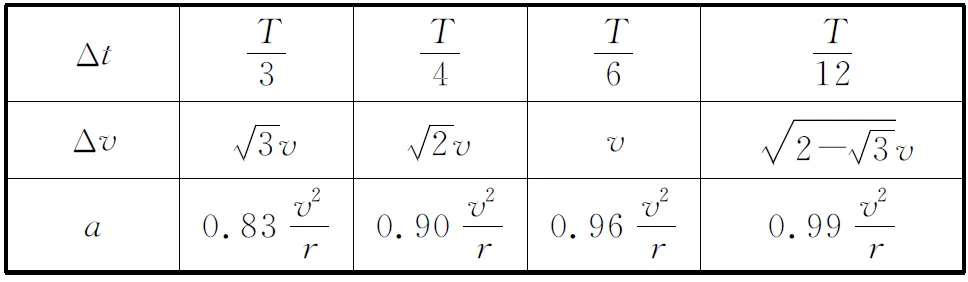
表5

教师:当Δt取值不断变小,速度变化量Δv的方向与tA时刻的速度方向关系如何变化?

学生:逐渐趋向于垂直且指向圆心．

教师:当时间Δt无限趋向于0时，

(1) 速度变化量Δv的方向与tA时刻速度的方向是否垂直?

学生:垂直.

(2) 加速度方向与tA时刻的速度方向是否垂直?

学生:垂直.

(3) 此加速度能否认为是tA时刻的瞬时加速度?

学生:可以.

(4) 根据表2中的加速度数据猜想:tA时刻的加速度大小为何值?

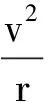
教师:如何证明此猜想?

学生:Δt取值趋向于0,用Δt时间内的加速度代替tA时刻的加速度.

教师:当Δt取值逐渐变短直至趋向于0,圆心角Δθ逐渐变小直至趋向于0,其对应的弧长与弦长关系如何?

学生:两者长度越来越接近直至完全相等．

教师:研究应以实际数据为准,以半径r=1m的圆为例,圆心角及其对应弧长与弦长如表6所示,可以发现，当角度逐渐变小时,弧长SAB与弦长LAB越来越接近,两者之差除以弧长,其值不断变小,直至趋向于0;说明当圆心角趋于0时,可认为弦长等于弧长．

表6

教师:表7中,△AOB与速度矢量三角形关系如何?

学生:相似.

教师:同桌两人为一组,根据以上知识,推导tA时刻瞬时加速度表达式,并将推导过程填写入表7中．

表7

3 总结:始于问题、入于探究、终于问题、巧设铺垫,激发学生深入探究的欲望

教师:匀速圆周运动加速度表达式还有哪些形式?

学生:a=rω2.

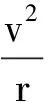
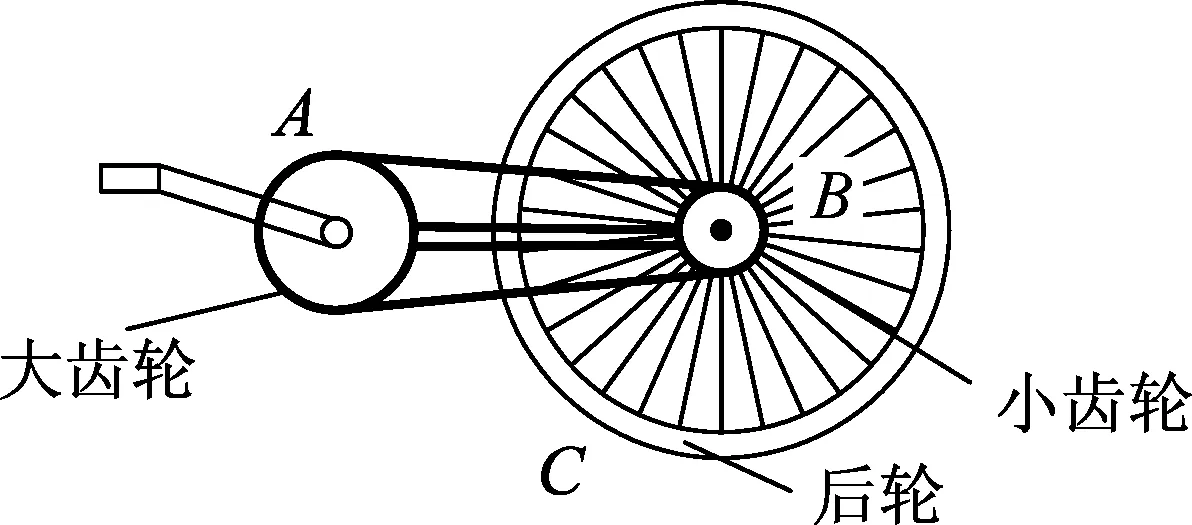
图1

教师:图1中A、B、C为大齿轮、小齿轮和后轮边缘处的3个点,哪两个点向心加速度与半径成正比?哪两个点向心加速度与半径成反比?

学生:B、C两点向心加速度与半径成正比;A、B两点向心加速度与半径成反比．

教师:为什么?

学生:A、B两点线速度相同,向心加速度与半径成反比;B、C两点角速度相同,向心加速度与半径成正比．

教师:很好,由以上的结论,能否说明向心加速度是由半径、角速度或线速度决定?

学生1:能.

学生2:不能.

教师:到底能还是不能,我们下一节课接着讨论.

4 教学反思

“向心加速度”一节思维要求高,方法灵活、概念抽象,强调过程的连续性与逻辑性,适合分组讨论探究,体现物理核心素养中“科学思维”、“科学探究”、“科学态度与责任”的教学要求和理念;围绕以上教学要求,笔者在教学设计时力求做到两点: (1) 突出重点.匀速圆周运动速度矢量图要求较高,笔者从直线运动和一般的曲线运动的速度矢量图入手,由浅入深,使学生对速度变化量矢量图的作法与意义有深刻认识;确定匀速圆周运动加速度的方向也是教学重点,笔者通过将Δt的取值不断减小,引导学生观察矢量图中速度变化量方向与速度方向关系的变化进而判断瞬时加速度的方向,形象而有效. (2) 分解难点.推导向心加速度表达式是本节难点,笔者通过对Δt取值不断减小,引导学生分组计算Δt的特殊取值所对应的平均加速度,进而猜想瞬时加速度表达式,证明猜想时,通过列出圆心角减小时弦长与弧长的具体数值以及两者之间差异性的变化,减小学生抽象思维的难度,起到很好的分解难点的效果．融合物理核心素养的课堂教学是培养全面发展,终身学习公民的关键途径,体现广大物理教师为增强民族创造力所做的点滴努力,一切都在路上,任重而道远.

1 张维善等.普通高中课程标准实验教科书 物理必修2[M].北京:人民教育出版社,2007.

2 何述平.匀速圆周运动向心加速度的教学研究[J].物理教师,2011(12):21-24.

3 吴国来.“向心加速度”探究式教学的创新设计与思考[J].物理教师,2012(7):19-20.

2017-02-10)