基于SVD和罚函数约束的子阵级方向图控制

栾晓明，肖华飞

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨150001 )

基于SVD和罚函数约束的子阵级方向图控制

栾晓明，肖华飞

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨150001 )

对于子阵级自适应波束形成中旁瓣电平较高的问题，提出一种基于奇异值分解和罚函数约束(SVD-PFC)的子阵级自适应方向图控制算法。该算法通过对输入数据进行奇异值分解，得到干扰子空间和噪声子空间，通过干扰子空间修正约束矩阵和约束响应矢量，可在小快拍情况下有效抑制干扰，同时结合罚函数对自适应方向图约束，使其逼近期望静态方向图。该算法具有良好的副瓣特性，提高了小快拍情况下输出的信干噪比，仿真实验证明了该算法的可行性和有效性。

自适应方向图控制；奇异值分解；罚函数；子阵级

0 引言

子阵级自适应波束形成可以有效地抑制干扰[1-3]，但在快拍数目较少的情况下，主瓣波束容易变形，副瓣电平会明显升高。自适应方向图控制技术可以在抑制干扰的同时进行低副瓣控制，一定程度上可抵消自适应加权矢量不能适应突变而带来的性能下降[4-7]。文献[8-9]提出罚函数法来增加一个约束，使方向图逼近静态方向图而降低副瓣。文献[10-13]提出基于特征向量的线性约束最小方差的自适应方向图控制算法，有效抑制干扰，降低旁瓣。这几种都是主要针对阵元级。在子阵级上，文献[13-16]提出基于子阵的划分方法，抑制旁瓣电平，但会造成一定的输出信干噪比损失。文献[17]提出一种基于子空间投影和最优失配检测法，可在没有干扰的情况下得到静态方向图。文献[18]提出基于阵列特征空间重构的方法，需要求解信号协方差矩阵并对其进行分解，运算量较大。文献[19]提出在子阵级噪声归一化的基础上，进行正交投影，抑制旁瓣电平。

上述算法在抑制干扰的同时控制副瓣特性，但存在小快拍数时，主瓣变形，副瓣起伏较大的问题。此次提出一种基于奇异值分解和罚函数约束(SVD-PFC)的子阵级自适应方向图控制算法，可在小快拍条件下抑制干扰使其逼近期望静态方向图，主瓣保形，旁瓣降低，并能够获得较好的信干噪比性能。

1 子阵信号模型

设有一个M阵元的等间距直线阵，将其不均匀地划为L个子阵，波束指向为θ0，设有K个远场干扰入射信号，干扰信号的波达方向为θi，其中i=1,2,…,K。阵列从M维变换为L维的变换矩阵为：

T=Φ0T0,

(1)

(2)

式中，T0为M×L维的子阵形成矩阵，此矩阵的列向量两两相交，只有第l列中与第l个子阵中阵元序号相对应的元素值为1，其余元素值为0。Φ0表示阵元级的移相处理，d为阵元间距，λ表示波长。

在子阵级上，采用LCMV进行波束形成，求得常规子阵级自适应权矢量：

(3)

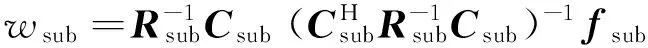
(4)

(5)

式中，Csub为子阵级的约束矩阵，fsub为约束响应矢量，R为阵元级接收协方差矩阵。

在子阵级采用LCMV的常规算法，虽然可以抑制干扰，但在快拍数有限的情况下，其方向图主瓣容易发生变形，旁瓣电平升高。

2 SVD子阵级自适应方向图控制算法

假设子阵级只有理想噪声，并无干扰，可得理想噪声下的子阵级静态加权矢量为：

(6)

考虑阵列接收到快拍数为I，存在K个干扰信号，得到包含干扰和噪声的接收数据矩阵X，经过子阵级变换得到子阵级的接收数据Xsub，对其进行SVD分解得到：

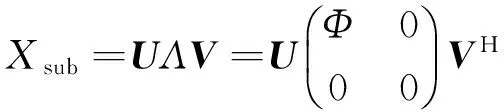
(7)

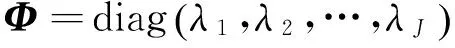
如果按照奇异值大小对U进行分解，有：

(8)

此时，Ui为子阵级的干扰子空间及UP为其子阵级的正交补空间矩阵，通过一些合适的信号源估计方法，可以确定有K个干扰，则在左奇异特征值矢量U中，与K个大奇异值对应的可以组成Ui，由剩下的左奇异特征值矢量组成UP。因子阵级干扰导向矢量asub和Ui的列向量张成为同一子空间，也就是子阵级的干扰子空间Ui和自适应加权矢量必须与正交，就可以在干扰方向上形成零陷，即：

(9)

此时子阵级的约束矩阵和约束响应矢量可以构造如下：

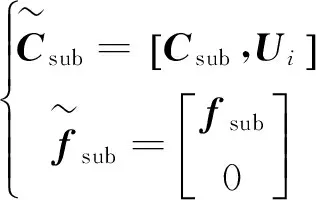
(10)

将式(10)中的约束矩阵和约束矢量带入式(6)中，得到基于SVD的子阵级自适应权矢量：

(11)

基于SVD的子阵级自适应权矢量，将加权矢量置于噪声噪声子空间内，利用噪声子空间和干扰子空间的正交性抑制干扰，解决了小快拍下噪声子空间小特征值发散的问题，因此可以一定程度上抑制干扰，主瓣保形。但由于子阵的不均匀划分，子阵级的接收数据并不一致，旁瓣电平仍然较高。

3 基于SVD和罚函数约束的自适应方向图 控制算法

在子阵级，考虑加权静态方向图的向量wsub_q，对子阵级自适应进行加权向量为wsub，则子阵级罚函数约束定义如下：

(12)

(13)

(14)

式中，asub(θ)=THa(θ)，为子阵级的导向矢量，h(θ)是一个合适的非负加权函数，在实际应用中常被定义为θ的偶函数。可以看出罚函数E是个能量函数，反映自适应方向图与期望的静态方向图之间的差异。

利用线性约束最小方差准则，对子阵级自适应权矢量进行约束的情况下，使得罚函数E能量最小，自适应权矢量的最优化问题为：

(15)

可以求得自适应权矢量为：

(16)

将式(10)的约束矩阵和约束响应矢量，代入式(16)可得SVD-PFC算法的自适应加权矢量。

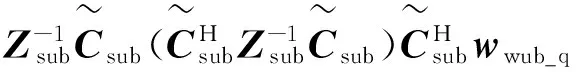
(17)

与式(11)的基于SVD算法的加权矢量的波束形成相比，采用式(17)的SVD-PFC算法的子阵级自适应波束形成，通过罚函数进一步约束自适应方向图，在抑制干扰的同时，能够使得自适应方向图逼近期望的静态方向图，进一步地降低旁瓣电平。

4 仿真结果分析

本文对子阵级常规算法、SVD算法和SVD-PFC算法的阵列方向图和输出信干噪比进行仿真，对比分析几种算法的性能。仿真实验假设一均匀直线阵，阵元间距为半波长，阵元个数为48，子阵数目为10，阵元不重叠，子阵阵元个数依次为[2 2 2 10 3 5 5 3 10 2 2 2]。

实验1：假设波束指向为0o，信噪比为10 dB，干扰入射方向为-22°、12°，信干比均为-30 dB，快拍数目为25。常规算法、SVD和SVD-PFC算法的仿真结果如图1所示。

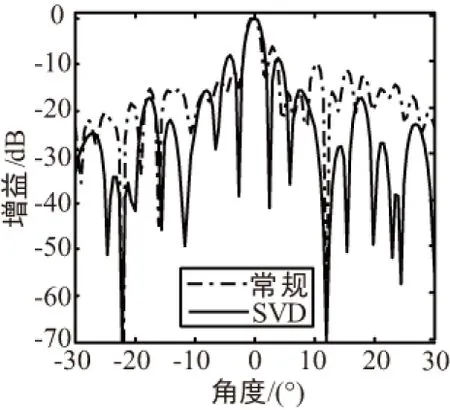
(a) 常规算法和SVD算法

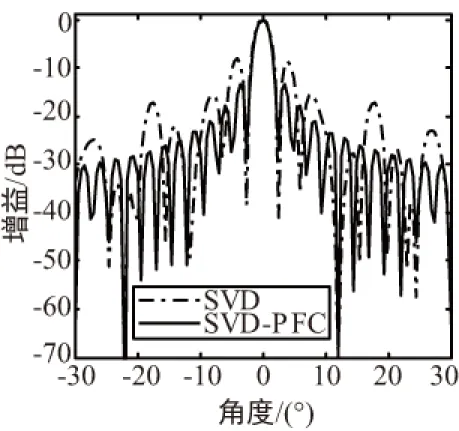
(b) SVD算法和SVD-PFC算法

由图1可知，在小快拍情况下，常规算法虽然在干扰方向上形成零陷，但主瓣明显发生恶化，出现指向偏移，旁瓣电平升高，而只采用SVD的算法可以很好地保持主瓣方向图。SVD算法的旁瓣电平保持-8 dB不变，而常规算法的旁瓣电平为-6 dB，2种算法的零陷深度都达到-70 dB、-75 dB左右。相比常规算法，SVD算法在快拍变化时，能够保持主瓣不发生恶化，但旁瓣电平略高。SVD-PFC算法的旁瓣电平约-13.3 dB，比SVD算法低5 dB左右，两者的零陷深度也几乎一样。

实验2：期望信号入射方向为0°，信噪比为10 dB，干扰信号入射方向为-15°、20°，信干比均为-30 dB，输出SINR随快拍数变化如图2所示。

由图2可知，3种算法的SINR都随着快拍数目增大而增大，SVD-PFC算法和SVD算法在快拍数20左右，SINR就趋于平缓。而常规算法在快拍数60以后，才逐渐升高到平缓的范围。其中在快拍数目小于40的情况下，SVD算法、SVD-PFC的算法的输出SINR要比改进前的要好。但是在快拍数目接近40左右，常规算法的SINR开始高于SVD算法，而改进后的SVD-PFC算法的SINR始终都高于常规算法和SVD算法，验证了结合SVD和罚函数的SVD-PFC算法可以有效地提高输出SINR。

图2 SINR随快拍数目变化

实验3：设期望信号入射方向为-40°～40°，信噪比为10 dB。干扰信号入射方向为-15°、20°，信干比均为-30 dB。输出的SINR如图3所示。

图3 输出SINR随角度变化

从图3中可以看到，在同一波束指向处，SVD算法的SINR略低于常规算法，但是通过罚函数改进SVD算法得到的SVD-PFC算法则始终略高于常规算法。

实验4：期望信号入射方向为0°，干扰入射方向为-15°、20°，信噪比为10 dB，在不同快拍情况下，最大旁瓣电平随信干比SIR的变化如图4所示。

从图4可以看出，在不同快拍情况下，常规算法的最大旁瓣电平随着信干比的变化上下起伏波动很大，而SVD-PFC算法的最大旁瓣电平值保持在-13.2 dB左右，表明了SVD-PFC算法克服快拍数对自适应波束形成的影响，具有保持静态方向图副瓣的特性。

图4 最大旁瓣电平随信干比SIR变化

5 结束语

针对小快拍数情况下，子阵级自适应波束形成方向图的主瓣变形，旁瓣电平升高问题，本文提出的SVD-PFC算法，通过SVD对子阵级接收数据分解，得到干扰子空间和噪声子空间，修正子阵级的约束矩阵和约束响应矢量，结合罚函数约束的子阵级自适应方向图控制算法。可在小快拍数时，主瓣波束保形，抑制干扰并保持静态方向图的副瓣特性，同时获得比较好的输出SINR。

[1] Nickel U R O. Subarray Configurations for Interference Suppression with Phased Array Radar[C]∥ Communications and Radar. Paris,France:Proc. of Intel. Conf. on radar,1989:82-86.

[2] Ferrier J M. Antenna Subarray Architectures And Anti-jamming Constraints[C]∥ Proc. of Intel. Conf. on Radar,Atlanta,USA,1994:466-469.

[3] Nickel U. Monopulse Estimation with Subarray-adaptive Arrays and Arbitrary Sum and Difference Beams[J]. IEE Proceedings-Radar Sonar and Navigation,1996,143(4):232-238.

[4] Combaud M. Adaptive Processing at the Subarray Level[J]. Aerospace Science & Technology,1999,3(3):93-105.

[5] Lombardo P,Cardinali R,Pastina D,et al. Array Optimization and Adaptive Processing for Sub-array Based Thinned Arrays[C]∥International Conference on Radar. IEEE,2008:197-202.

[6] 李洪涛. 自适应数字波束形成关键技术研究[D].南京:南京理工大学,2012.

[7] 张宗傲. 阵列雷达自适应主瓣干扰抑制算法研究[D].北京:北京理工大学,2015.

[8] Hughes D T,McWhirter J E. Penalty Function Method for Sidelobe Control in Least-squares Adaptive Beam Forming[C]∥SPIE's 1995 International Symposium on Optical Science,Engineering,and Instrumentation. International Society for Optics and Photonics,1995:170-181.

[9] Herbert G M. A New Projection Based Algorithm for Low Sidelobe Pattern Synthesis in Adaptive Arrays[C]∥ Radar. IEEE Xplore,1997:396-400.

[10]李洪涛,贺亚鹏,朱晓华,等. 基于特征向量的线性约束最小方差自适应方向图控制[J]. 南京理工大学学报(自然科学版),2011,35(4):529-533.

[11]苏保伟，王永良，周良柱. 基于 LCMV 线性约束的自适应方向图控制[J]. 电子与信息学报，2008，30(2):282-285.

[12]李荣峰，赵士锋，丁前军. 一种基于线性约束的自适应方向图控制方法[J]. 雷达科学与技术，2009,7(2)：139-142.

[13]Nickel U R O. Subarray Configurations for Digital Beamforming with Low Sidelobes and Adaptive Interference Suppression[C]∥ Radar Conference,1995. Record of the IEEE 1995 International,1995:714-719.

[14]许志勇,保铮,廖桂生. 一种非均匀邻接子阵结构及其部分自适应处理性能分析[J]. 电子学报,1997(9):20-24.

[15]陈子欢,刘刚,蒋宁. 一种新的子阵结构及其自适应性能分析[J]. 电子信息对抗技术,2006,21(3):33-37.

[16]熊子源,徐振海,张亮,等. 阵列雷达最优子阵划分研究[J]. 雷达科学与技术,2011,09(4):370-377.

[17]Lombardo P,Pastina D. Pattern Control for Adaptive Antenna Processing with Overlapped Sub-arrays[C]∥ Radar Conference,2003. Proceedings of the International. IEEE,2003:188-193.

[18]杨志伟,贺顺,廖桂生,等. 子空间重构的一类自适应波束形成算法[J]. 电子与信息学报,2012,34(5):1115-1119.

[19]Hu X, Guo L,Li S,et al. Improved Orthogonal Projection Adaptive Beamforming Based on Normalization at Subarray Level[C]∥ Iet International Radar Conference,2015:14-16.

Subarray Level Pattern Control Based on Singular Value Decomposition and Penalty Function Constraint

LUAN Xiao-ming，XIAO Hua-fei

(School of Information and Communication Engineering,Harbin Engineering University,Harbin Heilongjiang 150001,China)

To solve the problem of high sidelobe in adaptive beamforming at subarray level,an adaptive pattern control algorithm based on singular value decomposition and penalty function constraints (SVD-PFC) at subarray level is proposed. The algorithm obtains the interference subspace and noise subspace by the singular value decomposition of the input data,the constraint matrix and the constraint response vector are modified by the interference subspace,and the interference can be effectively suppressed in the condition of small snapshots. At the same time,it combines the penalty function to constrain the adaptive pattern to approximate the expected static pattern. The proposed algorithm has good sidelobe characteristics and improves the signal to interference plus noise ratio (SINR) of the output in the condition of small snapshots. Simulation results confirm the feasibility and effectiveness of the proposed algorithm.

adaptive pattern control;singular value decomposition;penalty function;subarray level

10. 3969/j.issn. 1003-3114. 2017.04.13

栾晓明,肖华飞. 基于SVD和罚函数约束的子阵级方向图控制[J].无线电通信技术,2017,43(4):56-59.

[LUAN Xiaoming,XIAO Huafei. Subarray Level Pattern Control Based on Singular Value Decomposition and Penalty Function Constraint [J].Radio Communications Technology,2017,43(4):56-59.]

2017-02-16

栾晓明(1963—)，男，教授，硕士生导师，主要研究方向：宽带信号检测、处理与识别。肖华飞(1991— )，男，硕士研究生，主要研究方向：阵列天线、自适应信号处理。

TN820.1

A

1003-3114(2017)04-56-4