基于层次分析法的大型半自磨机磨矿性能优化
2017-06-27付开进于向军
李 风 付开进 于向军
(1.吉林大学机械科学与工程学院, 长春 130022; 2.昆明学院自动控制与机械工程学院, 昆明 650214)
基于层次分析法的大型半自磨机磨矿性能优化
李 风1付开进1于向军2
(1.吉林大学机械科学与工程学院, 长春 130022; 2.昆明学院自动控制与机械工程学院, 昆明 650214)
为提升大型半自磨机的磨矿性能,建立了半自磨机离散元模型,将离散元仿真结果和试验测试结果进行了对比,验证了所建离散元模型的合理性。在此基础上,研究了影响磨矿性能的主要因素及其影响规律,应用层次分析法构造了因素与指标之间的层次结构和判断矩阵,建立了磨矿性能评价指标预测模型。应用该模型优化了某大型半自磨机的主要磨矿性能影响因素,与优化之前对比,比功率和钢球与矿料总有效碰撞次数分别提高了10.78%、15.47%,衬板最大磨损高度降低了10.81%,综合磨矿性能提高了17.25%。
大型半自磨机; 磨矿性能; 层次分析法; 性能优化; 均匀设计法
引言
国内大型半自磨机优化设计方法尚不成熟,磨矿过程中,由于破碎矿料的能耗占磨机总能耗的比例较低,存在能耗和钢耗较高、衬板磨损造成更换频率过高的情况。因此,大型半自磨机磨矿性能参数的调试和优化是磨机行业的技术难题之一。
在磨矿性能优化方面,DJORDJEVIC等[1-2]和MALEKI-MOGHADDAM等[3]研究表明,衬板形状改变时,介质运动会发生较大变化。SILVA等[4]和El-RAHMAN等[5]在衬板形状的基础上引入了更多变量,改善了功率预测模型。针对颗粒间的碰撞大都是低能的问题[6-7],MORRISON等[8-9]提出了颗粒发生累积破碎的最小冲击能阈值,并对颗粒破碎概率进行了预测。DELANEY等[10]对半自磨机颗粒破碎的能量阈值进行了分析。针对钢球和矿料对衬板冲击和磨削而引起磨损,KALALA等[11]和FRANKE等[12]基于离散元法对衬板磨损特性进行了预测。REZAEIZADEH等[13-14]研究表明,衬板磨损会降低磨矿效果,可通过增加磨机转速进行改善。JONSÉN等[15-16]通过DEM-FEM耦合方法分析了衬板的变形。OWEN等[17]基于试验优化设计方法,研究了介质运动轨迹与不同影响因素之间的关系。
本文采用离散元法对大型半自磨机进行建模分析,模拟钢球运动轨迹,基于试验台对离散元模型进行合理性验证。研究各主要因素对磨矿性能的影响规律,结合均匀设计法和层次分析法对半自磨机影响因素进行优化分析。
1 离散元建模仿真及验证
1.1 结构简化与离散元模型建立
大型半自磨机运行中,筒体内矿浆很少,可以不考虑矿浆的影响,同时忽略钢球和矿料的轴向移动,因此截取轴向长度为500 mm的筒体建立离散元仿真模型。筒体和衬板结构参数如表1所示。

表1 大型半自磨机筒体和衬板参数
在离散元仿真过程中,钢球和矿料的材料属性及其碰撞参数如表2所示。
根据上述仿真参数,建立了离散元模型,筒体内颗粒的静态分布情况如图1所示。在图1中,不同直径的颗粒赋予了不同的颜色,直径125 mm的钢球和150、130、110、90 mm的矿料分别用G125和K150、K130、K110、K90表示,K150、K130、K110和K90分别占总矿料的35%、20%、15%和30%(质量分数)。

表2 钢球和矿料的材料属性和碰撞参数
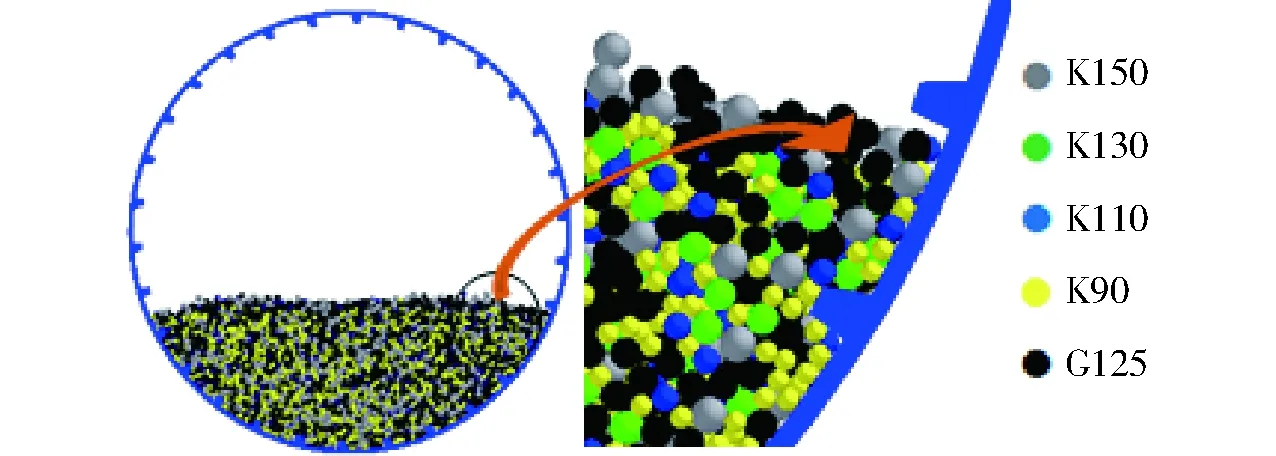
图1 钢球和矿料的静态分布及局部放大Fig.1 Static distribution and local magnification of steel ball and ore
1.2 理论计算与仿真结果对比
分析钢球运动规律时,假设介质在层层运动时,不产生相互干涉现象;层与层之间以及与衬板冲击碰撞、磨削时,忽略滑动效果;忽略矿料对钢球运动的影响;外层单个钢球可作为具有质量的质点。
假设钢球由脱离点A离开筒体时,由A点钢球的受力关系可知
mRω2=mgcosα
(1)
因此,最外层钢球的脱离角为
α=arccos(ω2R/g)
(2)
式中α——与z方向所成的脱离角ω——筒体角速度m——钢球质量R——筒体半径
钢球离开A点而上升的高度h(最高点与脱离点之间的垂直距离)为
h=(vsinα)2/(2g)
(3)
式中v——钢球脱离A点时的速度
以最外层单个钢球为分析对象,进行钢球脱离角和上升高度的分析。离散元仿真时间为25 s,钢球在25 s内的运动轨迹(离散元仿真中的x-z方向)如图2所示。
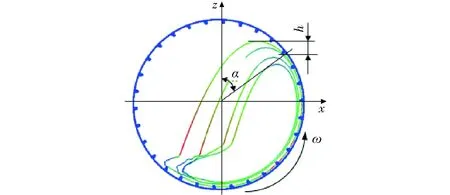
图2 单个钢球25 s内的运动轨迹Fig.2 Trajectory of single steel ball in 25 s
自磨机转速率为75%时,角速度ω=1.113 3 rad/s,由式(2)可知,该转速下钢球理论脱离角α为55.535°。在模拟过程中,最外层钢球刚离开筒体内壁时脱离角为56.800 1°,如图3所示。
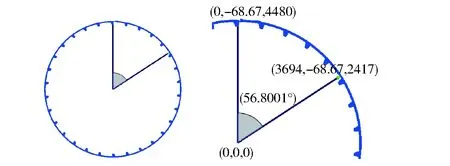
图3 介质脱离角及局部放大图Fig.3 Release angle and local magnification of medium
在4~25 s时间段内,该钢球在筒体竖直z方向的位移曲线如图4所示。
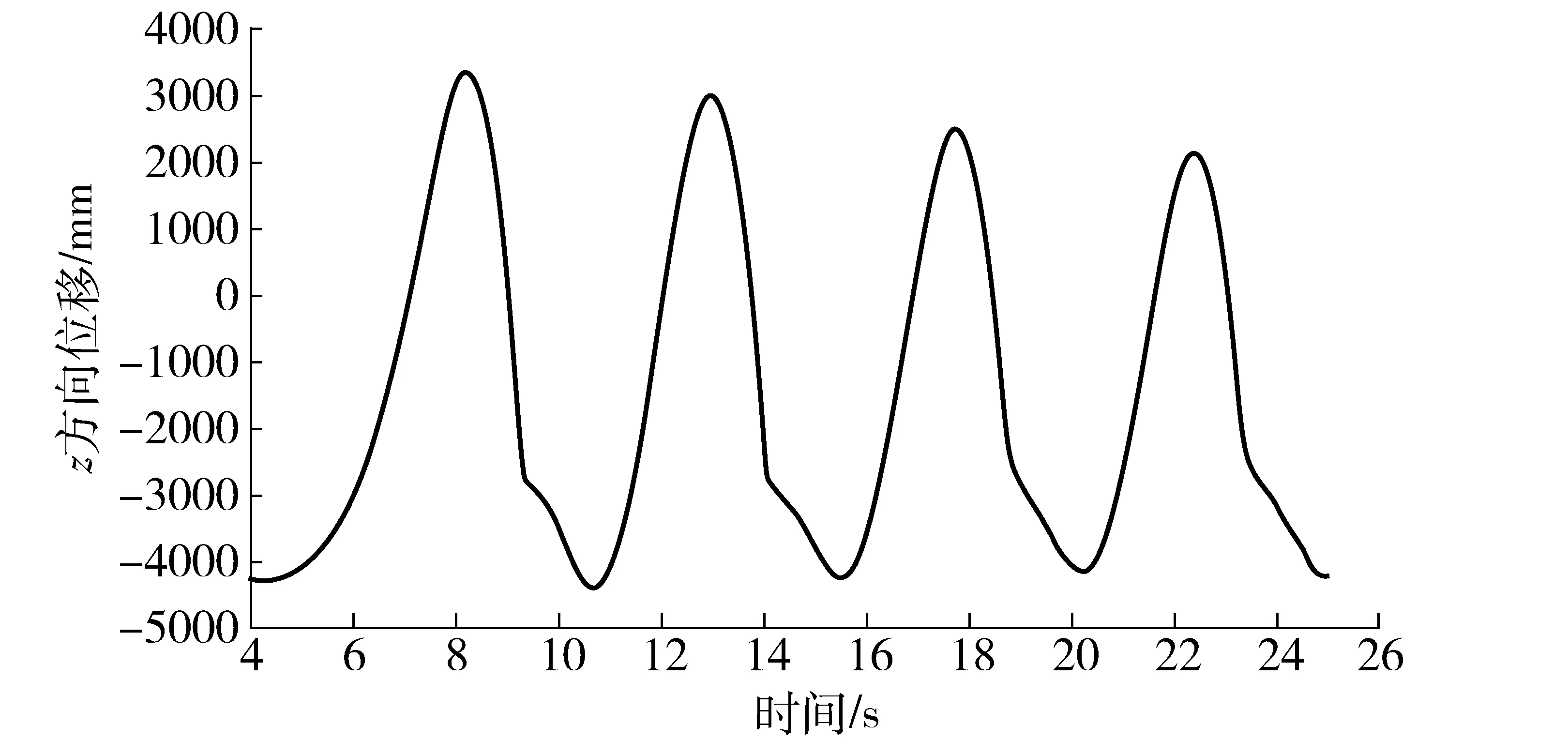
图4 钢球在z方向的位移Fig.4 Displacement of steel ball in z direction
由式(3)可知,钢球离开筒体后,理论上升高度为h=861 mm。由图3和图4可知,钢球在刚好离开筒体时的z方向高度为2 417 mm,且离开筒体后在8.18 s时刻上升到最大高度为3 357 mm。在仿真过程中钢球上升的高度为h=940 mm。由此可见,脱离角和上升高度的仿真值与理论值之间的相对误差分别为2.28%、9.18%。
1.3 离散元模型的验证
磨机试验台直径900 mm,长度1 400 mm,其主体结构如图5所示,试验台由电动机、减速器、齿轮、筒体和静压轴承等组成,筒体内安装了波形衬板。

图5 磨机试验台Fig.5 Test bench of mill
根据现有试验条件,选取钢球填充率φ为4%、7%、10%、13%、16%、19%、22%和25%共8种不同工况进行测试,得到不同工况时的钢球运动轨迹。通过离散元模型对这8种工况进行了模拟,仿真结果和试验测试的钢球运动状态结果如图6所示。
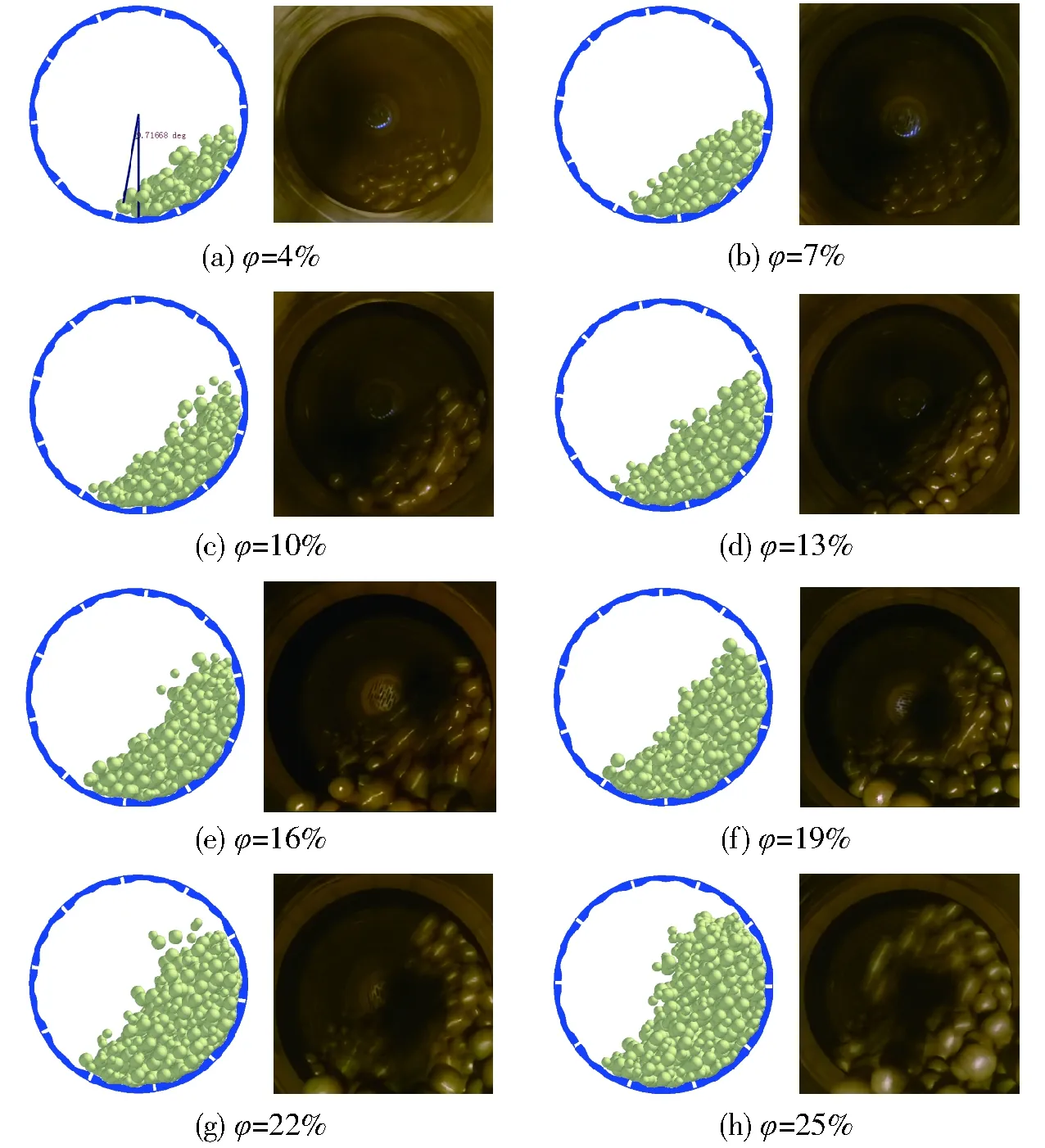
图6 钢球运动状态仿真结果与测试结果Fig.6 Simulation results and test results of steel ball motion
由图6可知,离散元仿真的钢球运动状态与试验测试运动状态一致。当钢球数量最低时,如图6a所示波形衬板并不能将钢球大幅提升,钢球只是逆时针偏转较小的角度;以图6中端口轴心位置为基准,钢球的上升高度明显低于轴心位置。当钢球数量越来越多时,碰撞也变得更加剧烈,且提升高度也越来越高,钢球脱离筒体时的高度逐渐超过端口轴心位置。如图6a所示,令θ为钢球底角区位置与竖直方向的夹角,不同填充率时θ的变化曲线如图7所示。
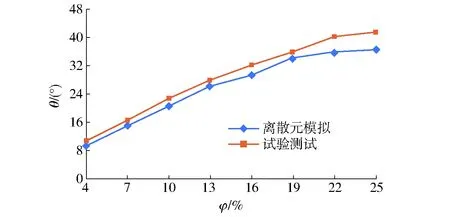
图7 离散元模拟和试验测试结果对比Fig.7 Comparison of discrete element simulation and test results
由图7可以看出,随着钢球填充率的增大,θ也呈逐渐递增的趋势,且增幅有所变缓;试验值略大于仿真值。总体来看,仿真值与试验测试值的变化规律一致,但在填充率25%时仿真值与试验值相对误差最大为11.44%,在填充率4%时相对误差最小为4.66%。误差产生原因为静压轴承支座的刚度不足以及试验时磨机整体产生振动。
2 影响磨矿性能的主要因素及其影响规律
2.1 基于均匀设计法的仿真方案选取
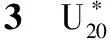
表(2011)试验方案及仿真结果
2.2 磨矿性能评价指标对应的最佳影响因素
依据表3数据,进行二次多项式逐步回归分析,优化后的比功率、钢球与矿料有效碰撞次数和衬板最大磨损高度预测模型分别为
y1=-8.987+0.411 7x1-8.314 5×10-4x1x3+
1.755×10-3x3x5-2.282 6×10-3x2x5
(4)
y2=-25 730.993+685.683x1+1.601x4x5-
(5)
1.124×10-3x4x5-2.458×10-4x1x4
(6)
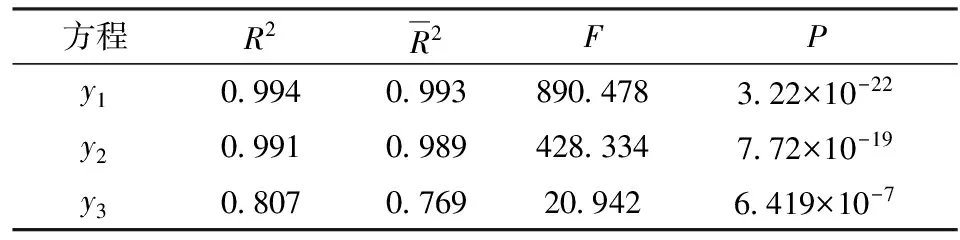
表4 回归方程参数
对式(4)~(6)进行全局搜索求解,可知,当转速率为84%、填充率为23%、衬板数量为38、高度为130 mm、倾角为35°时,比功率可取得最大值22.91 kW/t;当转速率为84%、填充率为23%、衬板数量为36、高度为208 mm和倾角为35°时,钢球与矿料总的有效碰撞次数最大为35 880,此时矿料的破碎效果最好;当转速率为60%、高度为220 mm、倾角11°时,衬板磨损高度最小为7.91×10-6mm,此时衬板的磨损程度最小。
3 基于层次分析法的综合磨矿性能优化
磨矿性能每一评价指标所对应的最佳影响因素组合并不一致,因此需要结合层次分析法,综合考虑3个指标对磨矿性能的影响,建立磨矿性能综合评价预测模型,得到最优影响因素组合。
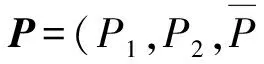
Pij=(xij-ximin)/(ximax-ximin)
(i=1,2;j=1,2,…,20)
(7)
式中xij——比功率、钢球-矿料有效碰撞次数实际值
(i=3;j=1,2,…,20)
(8)
式中yij——衬板最大磨损高度实际值
评价指标函数为
(9)
所得的数据集U可作为磨矿性评价指标集。
3.1 因素与指标间的层次结构
将所有影响因素和指标分组设层,该结构模型有3层,如图8所示。综合评价指标(磨矿性能)A处于目标层,而准则层为比功率C1、钢球-矿料有效碰撞次数C2和衬板最大磨损高度C33个指标,因素层为转速率B1、填充率B2、衬板数量B3、高度B4和倾角B55个因素。
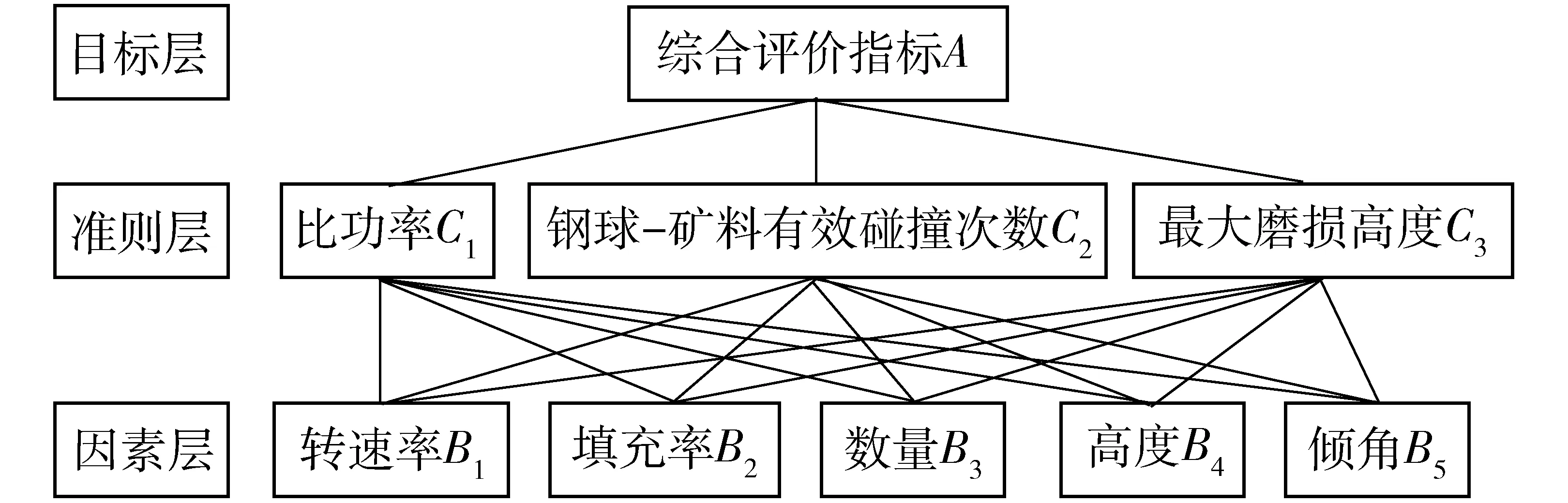
图8 因素与指标间的层次结构Fig.8 Hierarchy between factors and indicators
3.2 构造判断矩阵
依据层次结构模型,通过该层与上一层某一因素进行相对重要性比较,构造判断矩阵。在两因素M和N重要度分析时,采用1~9比例标度进行赋值,如表5所示。

表5 因素重要度对比
3.3 层次单排序及一致性检验
层次单排序是指根据判断矩阵计算对于层次结构中上一层某因素而言,本层次中各因素的相对重要性排序。当得到λmax后,需进行一致性检验,以保证评价结果的可靠性。检验方法为
CR=CI/RI
(10)
其中
CI=(λmax-n)/(n-1)
(11)
式中λmax——判断矩阵的最大特征值n——矩阵阶数CR——一致性比率CI——一致性指标RI——随机一致性指标
RI可通过表6查得[19]。

表6 随机一致性指标RI
若CR<0.1 ,则判断矩阵的不一致性程度在容许范围内,矩阵可以接受,其特征向量可作为权向量;否则需对矩阵作进一步调整。
3.4 层次总排序及一致性检验

(12)
对该层次总排序来说,同样也需对其进行一致性检验,检验公式为
(13)
同样当CR<0.1时,即认为层次总排序通过检验。
3.5 各层次结构的权重计算
在半自磨机实际运行中,应先保证矿石的破碎效果,因此钢球与矿料有效碰撞次数对总目标磨矿性能的影响相对较大。磨矿过程中,功耗所占比重较大,虽然由于衬板磨损等原因对磨机的经济性和磨矿性能也会造成一定的影响,但是如能有效降低功耗,可节约更多的成本。因此,在权值计算时,可认为比功率对目标层来说重要性稍大于衬板最大磨损高度,而又稍低于钢球与矿料有效碰撞次数。根据重要度定义,构建的判断矩阵为
(14)
根据和积法计算,得到3个指标的权重向量ωc=(0.297 2,0.539 0,0.163 8),最大特征值λmax=3.009 2,CR=0.007 9<0.1,满足一致性检验。同理,在比功率、有效碰撞次数和衬板最大磨损高度预测模型中,构建的判断矩阵分别为
(15)
(16)
(17)
和积法求解过程如下:首先将判断矩阵按列进行规范化处理
(18)
然后将规范化后的矩阵按行相加得到和向量
(19)
接着对矩阵进行行平均计算,可得权重向量
(20)
最后计算矩阵的最大特征值λmax。权重向量即是判断矩阵A的最大特征值λmax所对应的归一化后的特征向量。
(21)
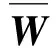
经过计算,因素层的5个因素相对磨矿性能评价指标来说,由表7可知,CR<0.1,满足一致性检验。

表7 判断矩阵结果
由层次总排序检验式(13)可得,CR=0.015<0.1,满足一致性检验。由式(12)可得,因素层因素对综合评价指标的权重分别为0.478 6、0.172 4、0.079 3、0.108 6和0.161 1。由此可知,对磨矿性能综合影响程度最大的是转速率,最小的是衬板数量。
3.6 磨矿性能综合预测结果与分析
比功率权重为0.297 2,钢球与矿料有效碰撞次数权重为0.539 0,衬板最大磨损高度权重为0.163 8,通过式(7)、(8)对3个指标无量纲化处理后,将数据代入式(9)中,计算磨矿性能综合评价指标集,所得结果为U=(0.478 2,0.871 7,0.298 3,0.673 3,0.230 1,0.574 4,0.800 6,0.446 9,0.699 7,0.273 2,0.662 9,0.250 8,0.499 8,0.790 2,0.357 1,0.837 8,0.309 5,0.533 7,0.122 0,0.483 7,0.877 7,0.378 6,0.717 7,0.224 5,0.572 9)。
通过逐步回归分析,磨矿性能综合评价指标集为
(22)
3.7 磨矿性能优化及对比分析
对上述最优磨矿性能的工况进行仿真分析,并与优化之前原工况下的指标值相比较,对比结果如表8所示。

表8 优化前后对比结果
优化后的比功率为21.79 kW/t、钢球与矿料有效碰撞次数为32 149、衬板最大磨损高度为4.363×10-5mm,可见比功率、钢球与矿料总有效碰撞次数分别提高了10.78%、15.47%,表明磨机功率得到了有效利用,矿料受到钢球冲击而产生的破碎效果也得到了改善;衬板最大磨损高度降低了10.81%,表明衬板的磨损程度相对减小。将表3中各影响因素组合分别代入式(22),所得结果与综合评价指标集U值进行对比,结合误差分析,得到原工况的综合指标值为0.838 6,而最优综合预测模型指标值为0.983 3,因此综合磨矿性能得到改善,提高了17.25%。
4 结论
(1) 建立了离散元模型,对比了脱离角和上升高度的理论值与仿真值;测试了钢球运动轨迹,并与离散元模拟结果进行对比,从而验证了离散元模型的合理性。
(2)基于均匀设计方法,进行二次多项式逐步回归分析和方差分析,得到影响因素与评价指标的数学模型及每一指标下的最佳影响因素组合。
(3)应用层次分析法,得到综合评价指标下的最佳影响因素组合:当转速率为84%、填充率为35%、衬板数量为52、高度为200 mm和倾角为35°时,比功率及钢球与矿料总有效碰撞次数分别提高了10.78%、15.47%,衬板最大磨损高度降低了10.81%,综合磨矿性能提高了17.25%。
1 DJORDJEVIC N. Discrete element modelling of the influence of lifters on power draw of tumbling mills[J]. Minerals Engineering, 2003, 16(4): 331-336.
2 DJORDJEVIC N, SHI F N, MORRISON R. Determination of lifter design, speed and filling effects in AG mills by 3D DEM[J]. Minerals Engineering, 2004, 17(11): 1135-1142.
3 MALEKI-MOGHADDAM M, YAHYAEI M, BANISI S. Converting AG to SAG mills: the Gol-E-Gohar Iron Ore Company case[J]. Powder Technology, 2012, 217: 100-106.
4 SILVA M, CASALI A. Modelling SAG milling power and specific energy consumption including the feed percentage of intermediate size particles[J]. Minerals Engineering, 2015, 70: 156-161.
5 EL-RAHMAN M K A, MISHRA B K, RAJAMANI R K. Industrial tumbling mill power prediction using the discrete element method[J]. Minerals Engineering, 2001, 14(10): 1321-1328.
6 WEERASEKARA N S, POWELL M S, COLE S, et al. Modeling breakage environment in tumbling mills using DEM and analyzing the outputs[C]∥DEM5: The Fifth International Conference on Discrete Element Methods, 2010: 477-483.
7 WEERASEKARA N S, POWELL M S, CLEARY P W, et al. The contribution of DEM to the science of comminution[J]. Powder Technology, 2013, 248: 3-24.
8 MORRISON R D, SHI F, WHYTE R. Modelling of incremental rock breakage by impact-for use in DEM models[J]. Minerals Engineering, 2007, 20(3): 303-309.
9 MORRISON R D, CLEARY P W. Using DEM to model ore breakage within a pilot scale SAG mill[J]. Minerals Engineering, 2004, 17(11): 1117-1124.
10 DELANEY G W, CLEARY P W, MORRISON R D, et al. Predicting breakage and the evolution of rock size and shape distributions in AG and SAG mills using DEM[J]. Minerals Engineering, 2013, 50: 132-139.
11 KALALA J T, BWALYA M, MOYS M H. Discrete element method (DEM) modelling of evolving mill liner profiles due to wear. Part II. industrial case study[J]. Minerals Engineering, 2005, 18(15): 1392-1397.
12 FRANKE J, CLEARY P W, SINNOTT M D. How to account for operating condition variability when predicting liner operating life with DEM—a case study[J]. Minerals Engineering, 2015, 73: 53-68.
13 REZAEIZADEH M, FOOLADI M, POWELL M S, et al. A new predictive model of lifter bar wear in mills[J]. Minerals Engineering, 2010, 23(15): 1174-1181.
14 REZAEIZADEH M, FOOLADI M, POWELL M S, et al. Experimental observations of lifter parameters and mill operation on power draw and liner impact loading[J]. Minerals Engineering, 2010, 23(15): 1182-1191.
15 JONSÉN P, PÅLSSON B I, HAGGBLAD H A. A novel method for full-body modelling of grinding charges in tumbling mills[J]. Minerals Engineering, 2012, 33: 2-12.
16 JONSÉN P, PALSSON B I, TANO K, et al. Prediction of mill structure behaviour in a tumbling mill[J]. Minerals Engineering, 2011, 24(3): 236-244.
17 OWEN P, CLEARY P W. The relationship between charge shape characteristics and fill level and lifter height for a SAG mill[J]. Minerals Engineering, 2015, 83: 19-32.
18 付开进. 大型半自磨机磨矿性能仿真及参数优化[D]. 长春:吉林大学, 2016. FU Kaijin. Simulation and parameter optimization on grinding performance of large-type SAG mill[D]. Changchun: Jilin University, 2016.(in Chinese)
19 ZHENG G, ZHU N, TIAN Z, et al. Application of a trapezoidal fuzzy AHP method for work safety evaluation and early warning rating of hot and humid environments[J]. Safety Science, 2012, 50(2): 228-239.
Optimization of Grinding Performance for Large-type Semi-autogenous Mill Based on Analytic Hierarchy Process
LI Feng1FU Kaijin1YU Xiangjun2
(1.SchoolofMechanicalScienceandEngineering,JilinUniversity,Changchun130022,China2.SchoolofAutomaticControlandMechanicalEngineering,KunmingUniversity,Kunming650214,China)
In order to improve the grinding performance of large-type semi-autogenous (SAG) mill, the trajectories of steel balls under different filling numbers were obtained through the test of the test bench of mill. Discrete element equivalent model of test bench was built and the trajectories of the steel balls were simulated. Test results and simulation results of equivalent model were compared. The comparisons showed that test results of trajectories of steel balls were consistent with simulation results. The main factors influencing the grinding performance and the influence law were studied. Mathematical model between factors and evaluation indexes was obtained through the quadratic polynomial stepwise regression analysis and analysis of variance. Optimal parameters combination was also obtained. The hierarchy structure and judgment matrix between factors and indexes were created by using the analytic hierarchy process. The prediction model of comprehensive evaluation index of grinding performance was established, by which the main design parameters of large-type SAG mill were optimized. Compared with the index values before optimization, the power per unit mass and total effective collision frequency between steel balls and aggregates were increased by 10.78% and 15.47%, respectively, and the maximum wear height of the lining was decreased by 10.81%. Meanwhile, the comprehensive grinding performance was increased by 17.25%.
large-type semi-autogenous mill; grinding performance; analytic hierarchy process; performance optimization; uniform design method
10.6041/j.issn.1000-1298.2017.06.052
2016-09-23
2016-10-18
国家自然科学基金项目(51265020)
李风(1962—),男,副教授,主要从事现代设计方法研究,E-mail: lifeng@jlu.edu.cn
于向军(1963—),男,教授,主要从事工程机械现代设计方法研究,E-mail: 582200523@qq.com
TD453
A
1000-1298(2017)06-0392-07
