冗余铺丝机械手逆运动学的拓扑流形分析

徐 朋 程锦翔 应明峰 李 奎

(南京航空航天大学机电学院， 南京 210016)

冗余铺丝机械手逆运动学的拓扑流形分析

徐 朋 程锦翔 应明峰 李 奎

(南京航空航天大学机电学院， 南京 210016)

针对优化的梯度投影算法在冗余铺丝机械手逆运动学求解问题中不一定存在最优解的问题，提出了一种拓扑流形算法。将冗余铺丝机械手的位形空间看作一个光滑流形，对耦合的位置逆解和姿态逆解进行解耦，然后分别针对位置子流形和姿态子流形进行仿真分析得到其相应的仿真拓扑流形。该方法可以将铺丝机械手的运动学问题抽象为数学中的曲面拓扑流形来研究，为铺丝机械手运动学在流形上分析提供了理论基础，同时也为后续铺丝机械手的最优化自运动控制提供了一种新的方法。最后以飞机S形进气道为例进行仿真，验证了所提方法的正确性。

机械手； 冗余； 拓扑； 流形； 进气道

引言

复合材料纤维铺放成型技术(Fiber placement, FP)是一种精确的复合材料先进制造技术[1-2]，既可以铺放规则曲面，也可以铺放不规则的自由曲面，同时大大提高了复合材料的性能，降低了复合材料的生产成本，减轻了复合材料成型制品的质量，不仅适合于航空航天、尖端武器装备等高科技产品的应用，同时也适合于工业、农业、医疗等高端机械领域的应用[3]。所以对于复合材料纤维铺放成型技术的工作母机——冗余铺丝机械手的研究已经成为当今先进制造技术的一个新的研究方向[4]。

铺丝机械手的运动学逆解是实现整个铺丝过程运动规划和运动控制的基础[5-6]，对于冗余铺丝机械手的逆运动学求解问题一般采用基于广义逆的梯度投影算法[7-8]，基于梯度函数的不同选择又出现了加权最小范数、最小奇异值、最小条件数、拉格朗日乘子等优化算法，根据梯度的定义可知以上算法所得逆运动学解不一定是冗余机械手的全局最优逆解，而冗余机械手拓扑流形包含了全部逆运动学解，所以得到了逆解的自运动流形[9-10]，就可以利用拓扑流形的性质从数学的角度来研究冗余铺丝机械手运动学的操作性能指标。

拓扑流形是一个没有全局坐标，局部坐标与欧式空间同态的拓扑空间[11]。以拓扑流形为核心和基础的现代微分几何学，在冗余机械手研究方面有着越来越多的应用和研究，特别是在复杂冗余机构中的非线性问题[12]，更容易得到具有几何和物理意义的结果，为后续自运动控制提供一定的理论基础。冗余机械手基于拓扑流形逆运动学求解问题，国内外诸多学者提出了很多算法[13-16]。

本文首先描述特殊结构8自由度串联铺丝机械手的拓扑结构[17-19]，在此基础上分别描述位置和姿态空间的拓扑流形，其次利用旋量理论结合参数方程的方法得到冗余铺丝机械手逆运动学解析解表达式[20-21]，最后通过仿真得到冗余铺丝机械手的位置空间流形和姿态空间流形，然后利用飞机S形进气道为例验证所提方法的正确性。

1 冗余铺丝机械手拓扑结构

图1中，滑动导轨、6自由度库卡机械手和旋转芯模共同组成了8自由度串联冗余机械手的闭环系统，由于冗余度的存在该系统有无数多个逆运动学解，逆解的变化呈现出拓扑流形的结构，通过对拓扑流形的研究可以更好地理解运动学逆解的数学本质，图2为其相应的拓扑结构。

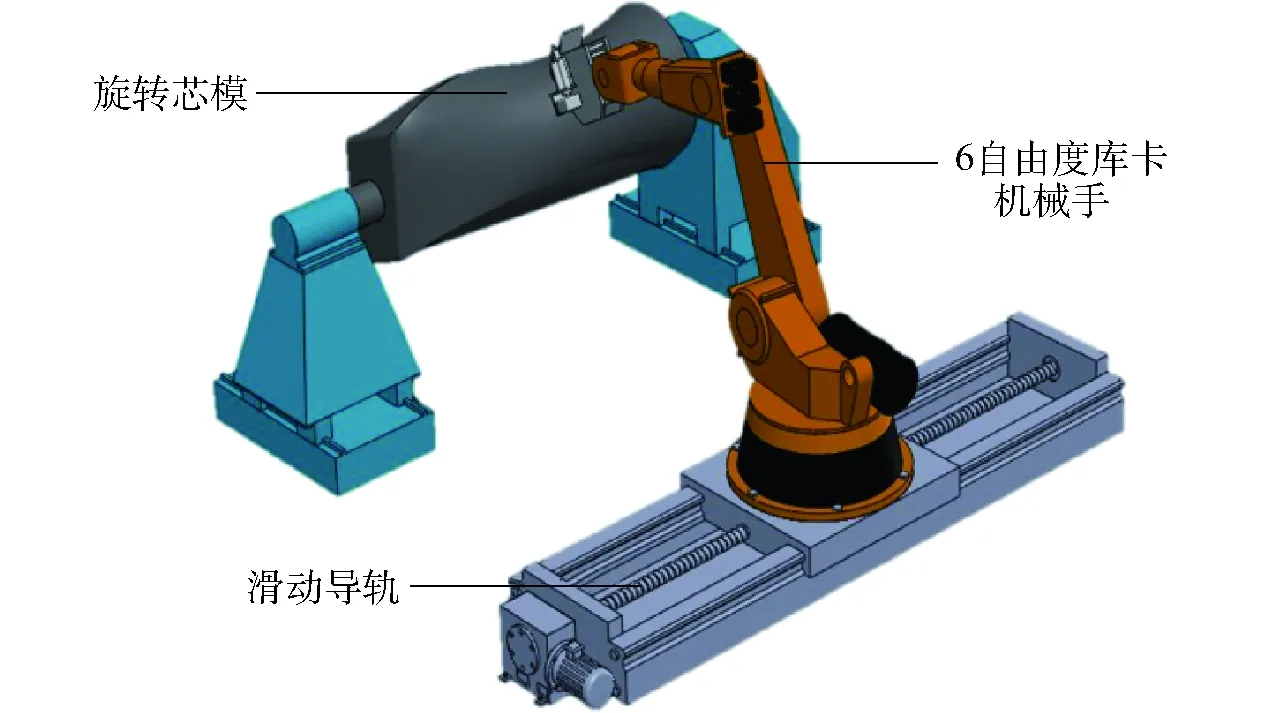
图1 8自由度冗余铺丝机械手模型Fig.1 An 8-DOF redundant fiber placement manipulator model

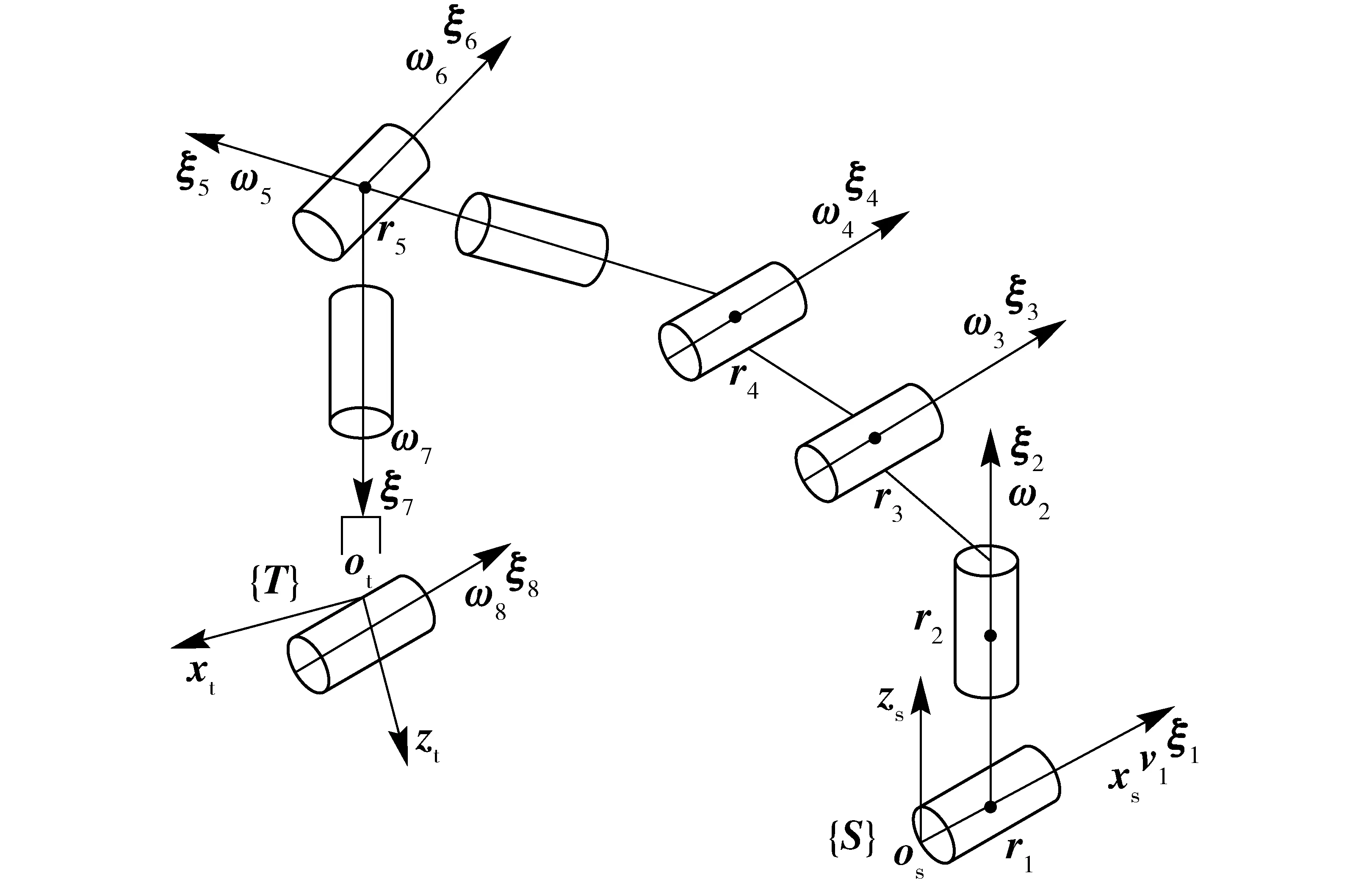
图2 8自由度冗铺丝机械手拓扑结构Fig.2 Topological structure of 8-DOF fiber placement manipulator

2 解空间拓扑流形

定义关节构型空间

C=C1C2C3C4C5C6C7C8

(1)

式中C1——移动关节构型空间C2～C7——各转动关节构型空间C8——末端旋转关节构型空间

定义f为关节构型空间C到工作空间W的映射函数，f由运动学正解可以得到，由于f是微分同态映射，则f:C→W和f-1:W→C是各阶偏导都存在的光滑映射，所以机械手关节所起的作用相当于数学中的函数，它实现了关节构型空间和末端执行器位姿工作空间之间的映射与逆映射。当滑轨和末端旋转关节运动时，8自由度铺丝机械手逆解将会呈现出曲面拓扑流形的结构，它是关于C的一个8维流形，包括了冗余铺丝机械手的全部逆解。

定义位置关节构型空间

Cwz=C1C2C3C4C5C6C7C8

(2)

定义位置关节工作空间流形

(Cwl,Fwl)={(θwl,fwl(θwl))/fwl(θwl)=P,θwl∈Cwz}

(3)

式中P——工具坐标系在惯性坐标系中的位置矢量

Fwl——运动学正解映射集合

fwl——运动学正解映射

θwl——位置关节运动流形

Cwl——位置关节工作空间流形，是一个8维拓扑流形

矢量P主要由位置关节d1、θ2、θ3、θ4、θ8决定，同时受到姿态关节θ5、θ6、θ7的影响。由于末端操作器工具坐标系与腕点第7关节坐标系连接固定，所以由工具坐标系可以得到铺丝机械手腕点第7关节坐标系的姿态和位置。

为了能将位置流形映射到三维空间，利用腕点矢量重新定义位置关节工作空间流形

C′wz=C1C2C3C4C8

(4)

(C′wl,F′wl)=(θ′wl,f′wl(θwl))/f′wl(θ′wl)=low(θ′wl∈C′wz)

(5)

式中low——从基坐标系原点到铺丝机械手腕点的矢量

C′wl——位置关节工作空间流形，是一个5维拓扑流形

以d1、θ8作为冗余变量可以将位置关节θ2、θ3、θ4映射到三维空间。

定义姿态关节构型空间

Czt=C2C3C4C5C6C7C8

(6)

定义姿态关节工作空间流形

(Czl,Fzl)=(θzl,fzl)/fzl(θzl)=(p,xT,zT) (θzl∈Czt)

(7)

式中xT、zT——末端工具坐标系的姿态Czl——姿态工作空间流形

由于Czl是一个7维拓扑流形，同样不能在三维空间直观展示，所以将位置关节θ2、θ3、θ4对腕关节姿态的影响归结为一个关节的影响，定义为θ′4。

重新定义姿态关节工作空间流形

C′zt=C′4C5C6C7C8

(8)

(C′zl,F′zl)=(θ′zl,f′zl)/f′zl(θ′zl)=(low,x7,z7) (θ′zl∈C′zt)

(9)

式中x7、z7——第7关节沿x轴和y轴方向单位矢量，代表了第7关节姿态

C′zl——姿态关节工作空间流形

C′zl也是一个5维拓扑流形，以θ′4、θ8作为冗余变量同样可以将姿态关节θ5、θ6、θ7映射到三维空间。

重新定义的位置空间拓扑流形C′wl和姿态空间拓扑流形C′zl就可以分别表示为以腰肩肘关节θ2、θ3、θ4和以腕关节θ5、θ6、θ7为主的曲面流形的结构。

3 逆运动学求解

利用旋量理论对8自由度冗余铺丝机械手逆运动学进行求解，机械手的初始状态及各连杆间的尺寸参数如图3所示。

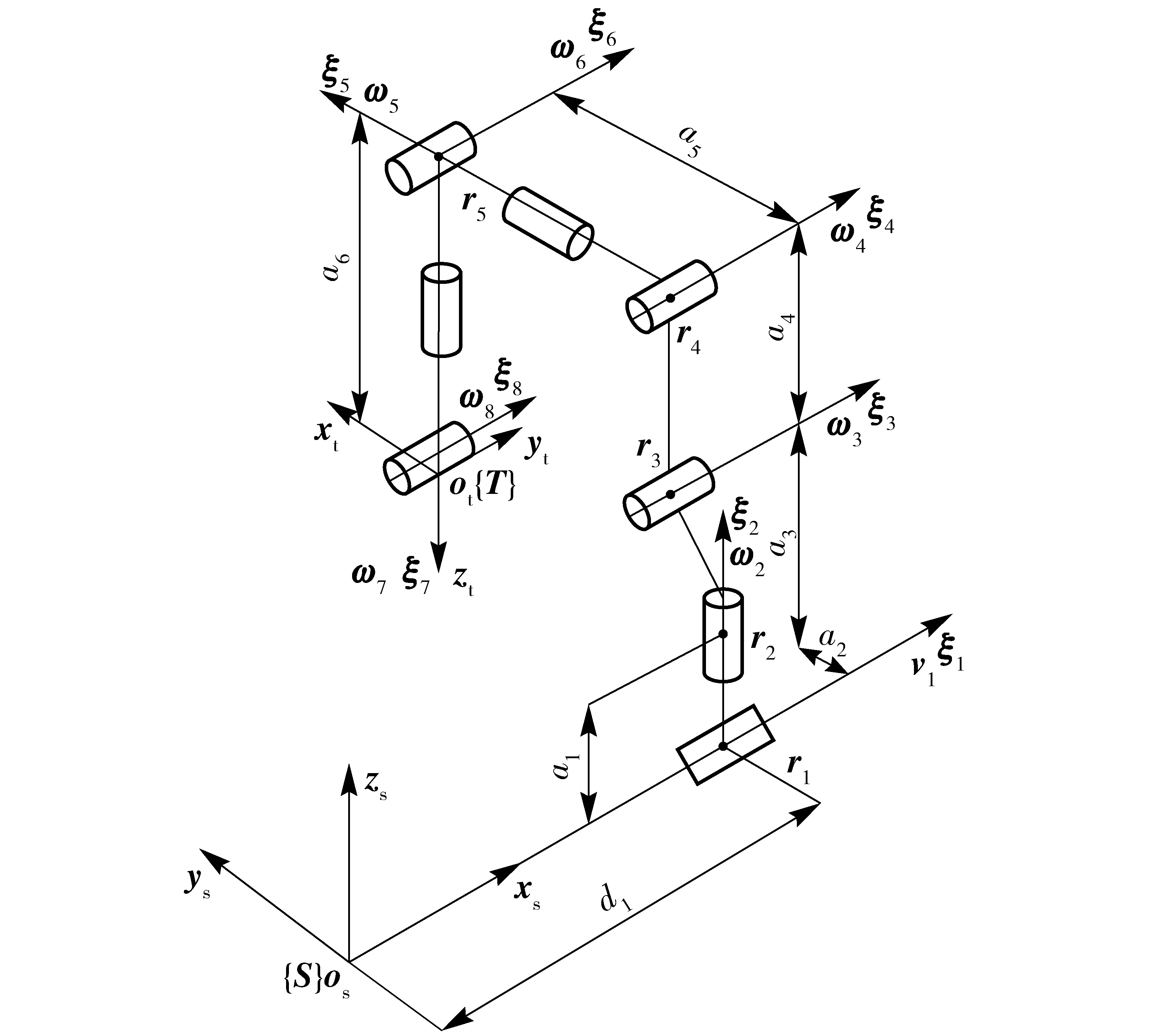
图3 冗余铺丝机械手初始状态Fig.3 Initial state of redundant fiber placement manipulator

初始状态工具坐标系{T}和惯性坐标系{S}之间的变换为

(10)

一般工作状态工具坐标系和惯性坐标系之间的变换为

gst(θ)=

(11)

式中θ8——第8关节旋转角度α——压辊轴线与芯模轴线的夹角r——铺丝轨迹点处的芯模半径a1～a6——铺丝机械手结构参数

将冗余关节设定为铺丝轨迹点在惯性坐标系下的横坐标d1和θ8，根据旋量理论及已知的Paden-Kahan子问题可以求得腰肩肘和腕部各关节解析表达式

θ2=arctan2(∓(qx-d1),±qy)

(12)

(13)

(14)

θ5=arctan2(q′x-d1,q′z-a3-a4)

(15)

(16)

θ7=arctan2(d1-q″x,a2+a5-q″y)

(17)

当冗余关节d1、θ8在规定范围内变化时，本文所得到的逆运动学解θ2、θ3、θ4、θ5、θ6、θ7均是以d1、θ8为变量的函数。冗余铺丝机械手8个关节变量都可以作为冗余变量，不同冗余变量下冗余铺丝机械手的运动构型是一致的，但是不同冗余变量下冗余机械手对应的自运动流形是不同的，为了实际铺丝过程中方便测量和计算，本文以d1、θ8作为冗余变量来计算逆解及拓扑流形分析，其中θ8耦合于gst(θ)。

4 仿真分析

定义臂形标志

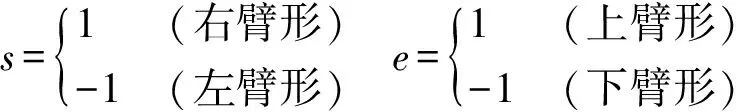
基于以上分析分别得到腰肩肘关节在不同臂形标志下的位置工作空间仿真拓扑流形，如图4所示。

图4 不同臂形标志下的位置空间仿真拓扑流形Fig.4 Position space simulation topological manifolds in different arm configurations

由图4所示的位置拓扑流形可以看到当铺丝机械手处于右上臂形和左上臂形时位置关节θ2、θ3、θ4具有较大的活动空间和灵活性，正常铺丝工作一般在上臂形进行。

腕关节θ5、θ6、θ7在不同臂形标志下的姿态工作空间仿真拓扑流形分别如图5、6所示。

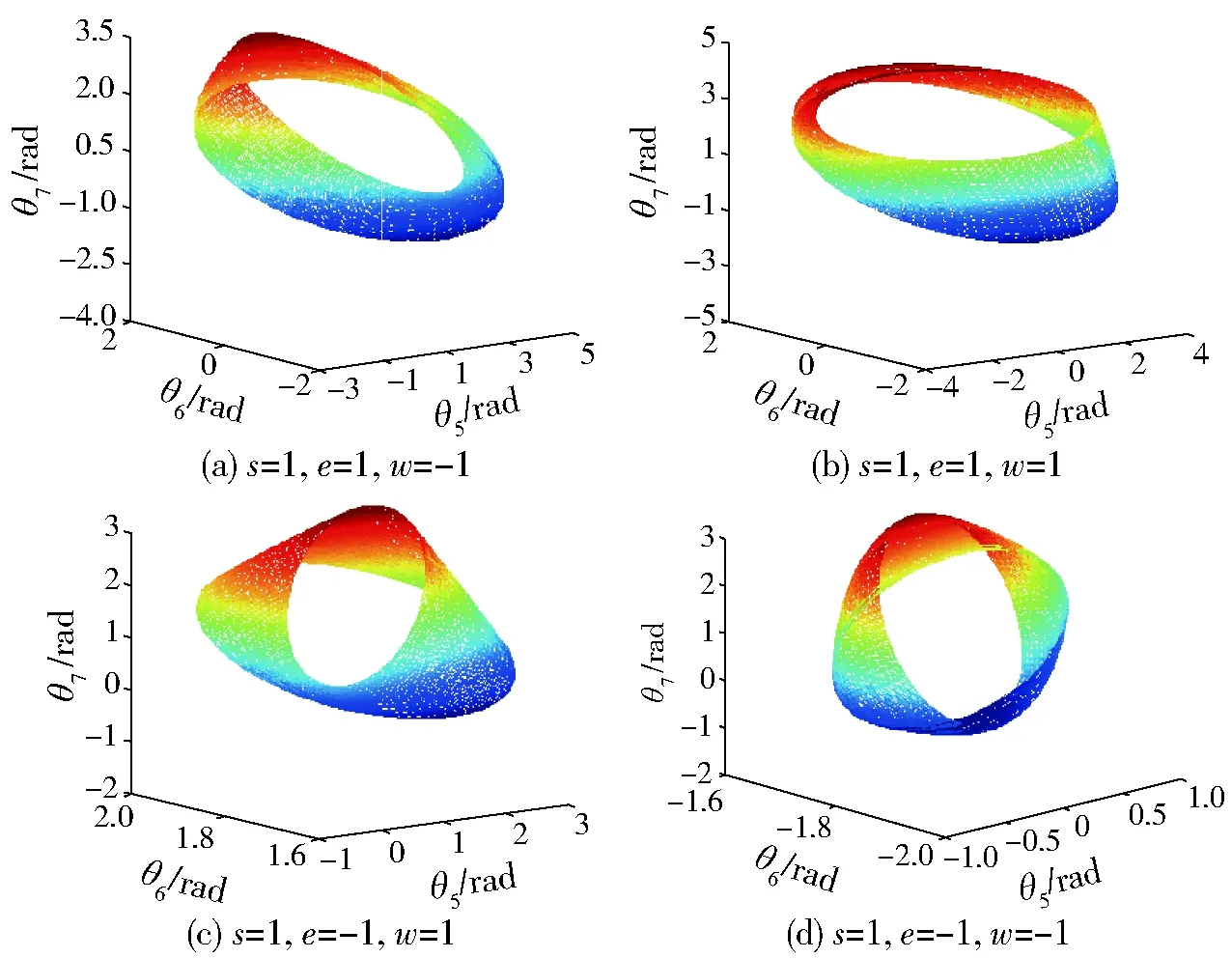
图5 右臂形状态下的姿态空间仿真流形Fig.5 Posture space simulation topological manifolds for right arm configuration

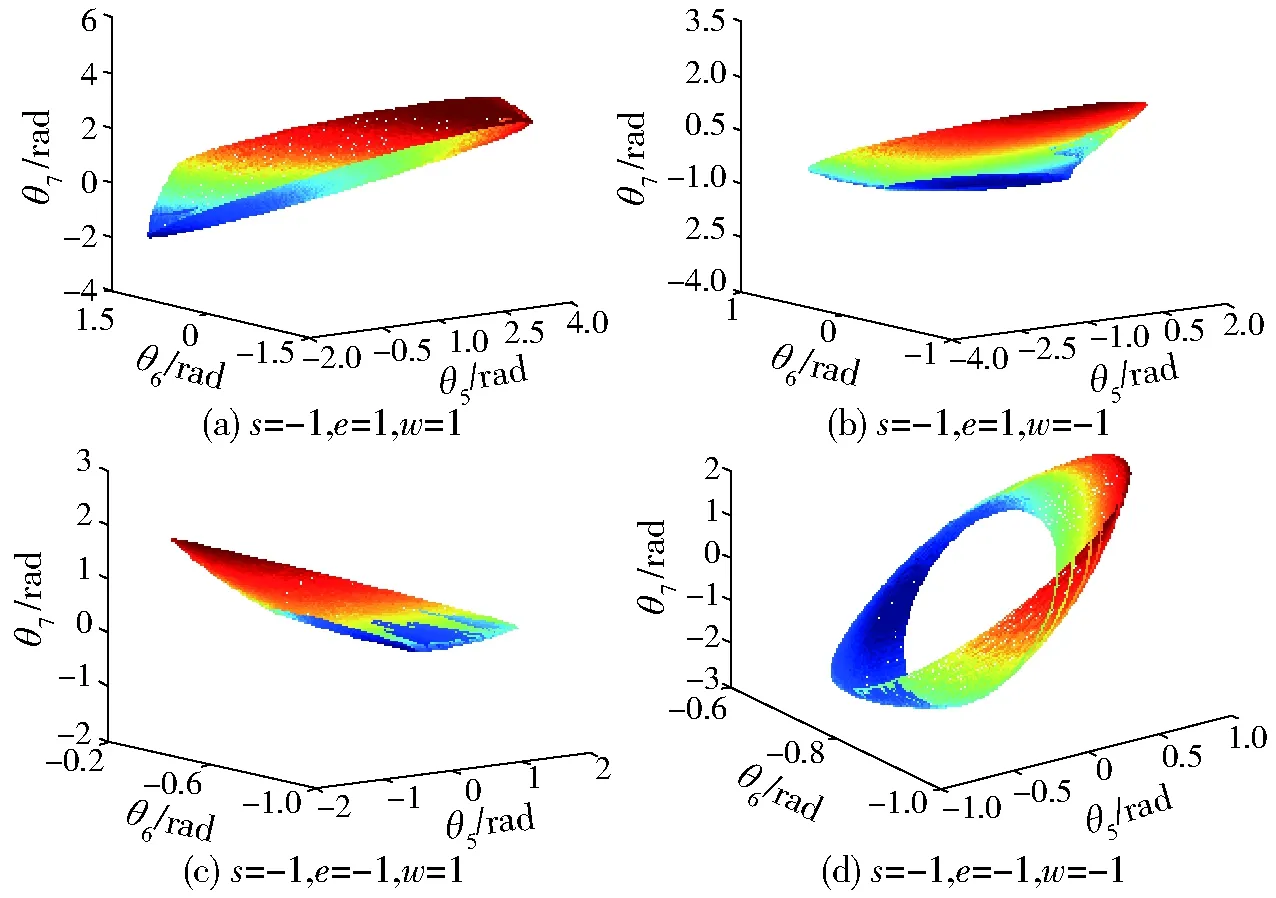
图6 左臂形状态下的姿态空间仿真流形Fig.6 Posture space simulation topological manifolds for left arm configuration

由图5、6可知当针对特定铺丝轨迹点时，铺丝机械手腕关节姿态处于右上臂形和左上臂形时具有较大灵活性，综合位置关节考虑可知当铺丝机械手处于右上臂形不翻腕的状态下具有最大工作空间，同时灵活性和避障碍能力也越强，在此基础之上可以利用拓扑流形的性质来研究铺丝机械手的关节逆解。拓扑流形用来研究由一组变量组成的空间特性，其上每一点处的切向量表征了该点的速度矢量，所有切向量的集合定义为该点的切空间，切空间与光滑函数的结合可以研究铺丝机械手的运动学性能指标，更有利于对铺丝过程的全局性优化。同时为了验证所得拓扑流形的正确性，在铺丝机械手处于右上臂形不翻腕的情况下，以飞机S形进气道轨迹曲线为例来验证所得拓扑流形的正确性，同时也利用拉格朗日优化的梯度投影算法得到了相应的仿真曲线作为对比，如图7所示。

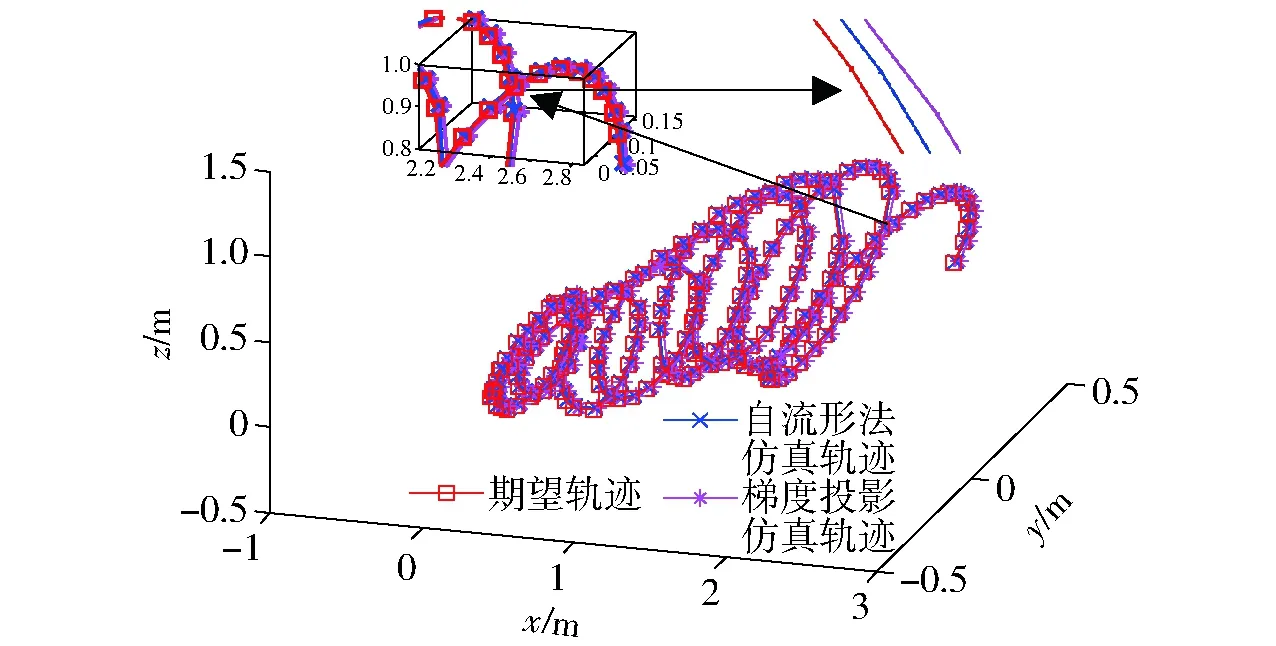
图7 飞机S形进气道仿真轨迹Fig.7 Simulation path for plane S-shaped inlet

由图7可知本文所用拓扑流形方法相比于拉格朗日优化的梯度投影法更接近于期望轨迹，证明了本文所用拓扑流形方法的正确性和合理性，同时本文在冗余铺丝机械手逆运动学和拓扑流形之间建立了合适的桥梁，为后续优化逆解的求取和最优自运动控制的选择奠定了基础。

5 结论

(1) 应用拓扑流形方法研究了冗余铺丝机械手的逆运动学解，分别在其位置工作空间和姿态工作空间得到了相应的仿真流形，将铺丝机械手的运动学问题成功转换为数学中的拓扑流形问题，这样就可以通过对拓扑流形的研究来得到铺丝机械手的最优逆解，为后续最优的自运动控制奠定基础。

(2)通过对飞机S形进气道仿真轨迹的对比，拓扑流形方法得到的逆运动学解相比于拉格朗日优化的梯度投影算法更适合于铺丝轨迹的要求，同时有效提高了铺丝过程的精确度。

1 陆楠楠, 肖军, 齐俊伟, 等. 面向自动铺放的预浸料动态粘性实验研究[J]. 航空学报,2014,35(1):279-286. LU Nannan, XIAO Jun, QI Junwei, et al. Experimental research on prepreg dynamic tack based on automated placement process[J]. Acta Aeronautica et Astronautica Sinica,2014,35(1):279-286.(in Chinese)

2 CHEN J H, CHEN-KEAT T, HOJJATI M, et al. Impact of layup rate on the quality of fiber steering/cut-restart in automated fiber placement processes[J]. Science and Engineering of Composite Materials,2015,22(2):165-173.

3 陈越超, 周晓军, 杨晨龙, 等. 厚截面复合材料局域孔隙超声检测方法[J/OL]. 农业机械学报,2015,46(6):372-378. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150653&flag=1. DOI:10.6041/j.issn.1000-1298.2015.06.053. CHEN Yuechao, ZHOU Xiaojun, YANG Chenlong, et al. Ultrasonic testing method for localized void defect identification in thick section composites[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015,46(6):372-378. (in Chinese)

4 段玉岗, 董肖伟, 葛衍明, 等. 基于CATIA生成数控加工路径的机器人纤维铺放轨迹规划[J]. 航空学报, 2014,35(9):2632-2640. DUAN Yugang, DONG Xiaowei, GE Yanming, et al. Robotic fiber placement trajectory planning based on CATIA CNC machining path[J]. Acta Aeronautica et Astronautica Sinica,2014,35(9):2632-2640. (in Chinese)

5 CHEN Jie, XU Wenjun, WANG Ben, et al. Fuzzy-adaptive PID based tow tension controller for robotic automated fiber placement[J]. Applied Mechanics and Materials,2014,643:48-53.

6 文立伟, 宋清华, 秦丽华, 等. 基于机器视觉与UMAC的自动铺丝成型构件缺陷检测闭环控制系统[J]. 航空学报,2015,36(12):3991-4000. WEN Liwei, SONG Qinghua, QIN Lihua, et al. Defect detection and closed-loop control system for automated fiber placement forming components based on machine vision and UMAC[J]. Acta Aeronautica et Astronautica Sinica, 2015,36(12):3991-4000. (in Chinese)

7 KOKURIN M Y. Stable gradient projection method for nonlinear conditionally well-posed inverse problems[J]. Journal of Inverse and Ill-Posed Problems,2016,24(3):323-332.

8 刘杰平, 杨朝煜, 方杰, 等. 改进的基于梯度投影的Gram观测矩阵优化算法[J]. 华中科技大学学报:自然科学版,2016,44(8):62-65. LIU Jieping, YANG Chaoyu, FANG Jie, et al. Improved optimization algorithm of the Gram measurement matrix based on gradient projection[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2016,44(8):62-65. (in Chinese)

9 AN H H, CLEMENT W I, REED B. Analytical inverse kinematic solution with self-motion constraint for the 7-DOF restore robot arm[C]∥2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics,2014: 1325-1330.

10 GE Xinfeng, ZHAO Dongbiao, LU Yonghua, et al. Study of dynamics performance index of the automated fiber placement robotic manipulator[J]. Journal of Information and Computational Science,2011,8(14):2975-2982.

11 HAUBERK S. Principal curves on riemannian manifolds[J]. 2016 IEEE Transactions on Pattern Analysis and Machine Intelligence,2016,38(9):1915-1921.

12 刘进.子流形平均曲率向量场的线性相关性[J]. 数学学报,2013,56(5):669-686. LIU Jin. Linear dependence of mean curvature vector fields of submanifold[J]. Acta Mathematica Sinica, 2013, 56(5):669-686. (in Chinese)

13 MOLL M, KAVRAKI L E. Path planning for minimal energy curves of constant length[C]∥Proceedings of the 2004 IEEE International Conference on Robotics and Automation, 2004,3:2826-2831.

14 BURDICK J W. On the inverse kinematics of redundant manipulators: characterization of the self-motion manifolds [C]∥Proceedings of the 1989 IEEE International Conference on Robotics and Automation, 1989:264-270.

15 赵建文, 杜志江, 孙立宁. 7自由度冗余手臂自运动流形[J]. 机械工程学报,2007,43(9):132-137. ZHAO Jianwen, DU Zhijiang, SUN Lining. Self-motion manifolds of a 7-DOF redundant manipulator[J]. Chinese Journal of Mechanical Engineering,2007,43(9):132-137. (in Chinese)

16 葛新锋, 赵东标. 7自由度自动铺丝机器人参数化的自运动流形[J]. 机械工程学报,2012,48(13):27-31. GE Xinfeng, ZHAO Dongbiao. Parameterized self-motion manifold of 7-DOF automatic fiber placement robotic manipulator[J]. Journal of Mechanical Engineering,2012,48(13):27-31. (in Chinese)

17 沈惠平, 曾氢菲, 李菊, 等. 典型并联机构拓扑结构特征分析[J/OL]. 农业机械学报,2016,47(8):388-398. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160851&flag=1. DOI：10.6041/j.issn.1000-1298.2016.08.051. SHEN Huiping, ZENG Qingfei, LI Ju, et al. Topological structure characteristic analysis for typical and practical parallel mechanisms[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2016, 47(8):388-398. (in Chinese)

18 韩刚. 从欧几里得空间到拓扑空间[J]. 高等数学研究,2015,18(4):8-10. HAN Gang. From euclidean space to topological space[J]. Studies in College Mathematics,2015,18(4):8-10. (in Chinese)

19 吴修云. 诱导的fuzzy拓扑生成序空间[J]. 模糊系统与数学,2015,29(3):84-90. WU Xiuyun. On induced fuzzy topogenous order spaces[J]. Fuzzy Systems and Mathematics,2015,29(3): 84-90. (in Chinese)

20 ZHENG F Y, HUA L, HAN X H. The mathematical model and mechanical properties of variable center distance gears based on screw theory[J]. Mechanism and Machine Theory,2016,101:116-139.

21 DAI J S. Screw algebra and lie groups and lie algebras [M]. 北京：高等教育出版社，2014:119-149.

Topological Manifolds Analysis for Inverse Kinematics of Redundant Fiber Placement Manipulator

XU Peng CHENG Jinxiang YING Mingfeng LI Kui

(CollegeofMechanicalandElectricalEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China)

A new topological manifolds method was proposed to solve the inverse kinematics problem of the redundant fiber placement manipulator. It improved the calculation precision compared with the optimized projected gradient method. A structure of smooth topological manifolds was presented by the inverse kinematics solution of redundant fiber placement manipulator, the simulation topological manifolds were obtained when the position sub-manifolds and posture sub-manifolds had a different simulation analysis for the redundant fiber placement manipulator model, it was like the function mapping in the mathematics from the manipulator joints space to the working space of the end effector. The tangent vector described velocity vector for each point on the topological manifolds, the gather of all these tangent vectors were defined as the tangent vector space on the point. The kinematics problems of the redundant fiber placement manipulator were abstracted to mathematically curved surface topological manifolds problem in the new method, it provided a new theoretical basis for manifolds analysis of the redundant fiber placement manipulator. Thus the subsequent optimization of inverse kinematics solutions manifolds problems were obtained by using self-motion curved surface manifolds theory in the mathematics, it provided a new method for improving the subsequent optimization self-motion control of the redundant fiber placement manipulator. The whole operating performance of the redundant fiber placement manipulator was improved greatly, and it would play a great role in promoting the quantity in the working fiber placement. The new method was verified by simulation of plane S-shaped inlet.

manipulator; redundancy; topology; manifolds; inlet

10.6041/j.issn.1000-1298.2017.06.051

2016-09-20

2016-10-19

国家重点基础研究发展计划(973计划)项目(2014CB046501)

徐朋(1982—)，男，博士生，主要从事冗余铺丝机械手的逆解及自运动流形研究，E-mail: xpnuaa@163.com

TP242.2

A

1000-1298(2017)06-0387-05