基于压实分析模型的土壤应力传递系数研究

贺亭峰 丛文杰 BELAL Eisa Adam，2 丁启朔 杨艳山 霍连飞

(1.南京农业大学工学院， 南京 210031； 2.扎林盖大学农业工程系， 扎林盖 06)

基于压实分析模型的土壤应力传递系数研究

贺亭峰1丛文杰1BELAL Eisa Adam1，2丁启朔1杨艳山1霍连飞1

(1.南京农业大学工学院， 南京 210031； 2.扎林盖大学农业工程系， 扎林盖 06)

机械压实是造成土壤退化的重要原因之一，研究并预测土壤应力有助于科学规划田间机械使用，缓解压实问题。基于分析模型预测土壤应力的关键在于选择合适的集中系数。然而在已有的研究中集中系数取值混乱，导致该模型使用时存在很大争议，其原因在于对该参数随土壤环境的变化缺乏规律性认识。本文通过对集中系数表达式的进一步推导，在理论上提出了能够代表土壤环境对集中系数影响的无量纲参数σz/σ0，定义为应力传递系数(STC)。基于水稻土和黄棕壤两种土壤，通过控制含水率和湿密度于室内重塑30种状态的土壤，在单轴压缩实验中运用土压力传感器测量计算应力传递系数，建立应力传递系数与土壤环境参数，如含水率、干密度和先期固结压力等之间的相关性分析。结果表明应力传递系数随土壤含水率的增大而增大，土壤初始干密度和先期固结压力与应力传递系数之间负相关性明显。根据所得应力传递系数计算相应土壤状态下的集中系数，其取值在1.20～12.39之间，与以往的研究结果相差不大，但包含了关于集中系数随土壤环境变化的具体信息。这意味着作为一个稳定可测的无量纲参数，应力传递系数为集中系数的计算提供了一个相对科学的方法，在定量描述土壤环境对集中系数影响的同时，完善了分析模型。

土壤压实； 分析模型； 集中系数； 土壤环境； 应力传递系数

引言

田间机械作业过程中，土壤-轮胎交互作用产生土壤应力改变土壤状态[1-4]造成的土壤压实是导致世界范围内土壤出现退化的重要原因之一[2,5-10]。研究并预测土壤应力可以科学规划田间机械的使用，缓解这一问题[2,11-12]。在以往的研究中，计算土壤应力的方法有仿真法(有限元和离散元)和分析模型法[2,13-14]。

与仿真法建立的土壤应力传递模型[15-17]相比，土壤压实分析模型在使用时因所需参数较少而被广泛运用[10,18-23]。然而现有的分析模型都是基于原始的Boussinesq方程，其假设土壤是均质、弹性、各向同性的介质[21]。实际上土壤介质是弹塑性体甚至粘弹塑性体，因此又引入了集中系数更精确地描述应力在土壤中的分布[24]。然而在实际应用中，集中系数的取值成为最大的问题。

SÖHNE[25]发现集中系数ν随含水率的增大而增大，提出土壤在“坚硬”、“中度”、“松软”3种条件下分别取值为4、5、6。RAM[26]利用重塑土实验控制土壤含水率和容重来探究集中系数的影响因素，发现容重从1.24 g/cm3变化到1.63 g/cm3的过程中，对应的集中系数从5.4减小到1.5。HORN等[27]在实验中证明集中系数的取值取决于先期固结压力，给出了集中系数的取值范围是6～9。在其他同类型的研究中，集中系数的范围是2.0～14.3[12,28-31]。即使针对集中系数变化趋势这一问题，也无法得到统一的认识。HORN等[28]和RÜCKNAGEL等[23]认为先期固结压力较大的土壤，集中系数更大，然而TRAUTNER[20]在实验中却得到了相反的结论。面对集中系数取值不一致性，无论是理论还是实验，都没有给出合理的解释。也正是因为这一原因，国内的土壤应力计算研究多使用仿真模型预测法[16-17]，关于分析模型预测法的应用鲜见报道。

集中系数受加载环境和土壤环境的双重影响[25,27,32]，KELLER等[12]认为：“土壤环境对集中系数影响的未知是分析模型预测土壤应力的主要障碍。”本文通过对集中系数表达式的进一步推导，在理论上提出能够代表土壤环境对集中系数影响的无量纲参数即应力传递系数(STC)；并设计室内重塑土实验，验证应力传递系数是否稳定可测；再建立其与土壤物理参数间的关系，来验证应力传递系数及由应力传递系数计算得到的集中系数ν是否确实受到土壤环境的影响。

1 理论

在使用分析模型预测土壤应力的研究中发现，应力预测值与实际测量值之间存在着较大差距[24-25,33]，故而将土壤视作弹塑性材料并引入了集中系数[24]。因此，土壤表面加载点正下方z点处的应力σz(kPa)为[24-25]

(1)

式中P——土壤表面加载点处载荷，kNR、z——土壤-轮胎接触面当量半径、加载点与正下方应力预测点间的距离，m

ν——集中系数，在初始的Boussinesq方程中取值为3

当土壤-轮胎接触面当量半径(R)确定时，对方程(1)积分以预测土体中任何位置处垂直方向的土壤应力。假设加载力均匀地分布在当量半径为R的圆形接触面，此时接触面正下方z处垂直方向的应力可表示为[24]

(2)

其中

σ0=W/(2πR2)

式中σ0——土壤的表面应力，kPaW——当量半径范围内的总载荷，kN

为了能更进一步的研究分析模型，推导出集中系数的表达式[24,28]

(3)

在恒定的加载条件下(R恒定)，可推导出集中系数ν

(4)

在式(4)中，集中系数是关于加载环境(R和z)和一个无量纲参数的函数。1/(1-σz/σ0)所代表的是加载应力在传入土体后到达位置z过程中单纯由土壤导致的应力衰减率，即σz/σ0为应力在土壤中的传递效率，定义为应力传递系数S(Stress transmission coefficient,STC)。因此，公式(4)变换为

(5)

由公式(5)可知，在加载条件一定的情况下，集中系数取决于应力传递系数，即取决于土壤自身的应力传递效率。由于土壤属于非弹性体，以上公式的推导均是假设土壤为弹塑性介质。

2 材料与方法

通过对重塑的水稻土进行单轴压缩实验，同时运用土压力传感器监测土壤应力，对土壤应力传递过程进行评价。在众多的研究中[14,19,24,29-31,34-35]，土压力传感器被用于量化土壤内部应力和表面应力间的关系。

2.1 土样的准备

实验所用水稻土取自南京农业大学浦口农场，水稻收获后从田间将耕作层土壤(0～15 cm)取回实验室，黄棕壤样品取自南京浦口老山地区丘陵缓坡非农业景观用地，2种土壤的理化指标如表1所示。将取回的土壤风干，破碎，过4 mm筛，根据汪攀峰等[36]的方法按照5%级差调配含水率为15%、20%、25%、30%、35%的水稻土土壤，按照3%级差调配含水率为13%、16%、19%、22%、25%的黄棕壤土壤。并分别密封于塑料膜中，静置24 h[37-38]。然后采用TAGAR等[38]的方法用φ50 mm×50 mm的环刀制备湿密度为1.1、1.3、1.5 g/cm3的土壤样品(土壤厚度50 mm)。在此之前还需在环刀内壁抹上一层凡士林以减弱土壤-内壁摩擦效应[39]。每种参数的土壤重复3次。

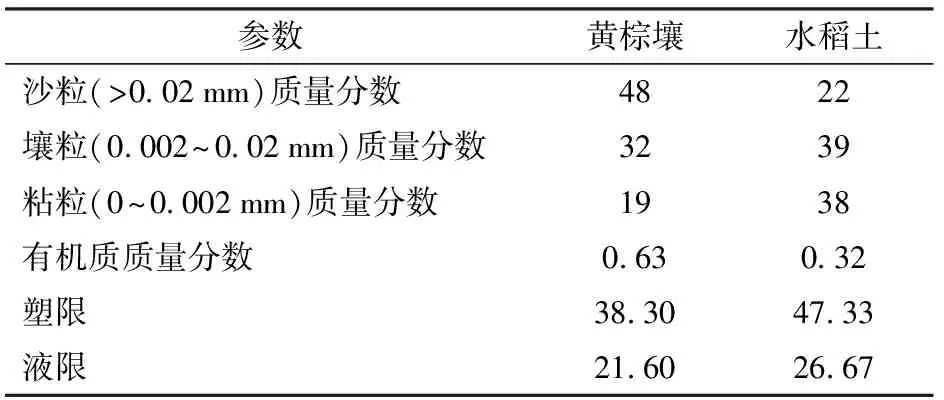
表1 土壤基本理化性质

2.2 监测土壤应力

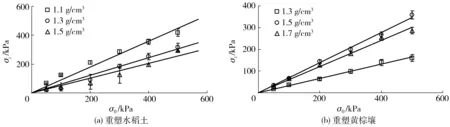
图2 一次加载过程中土壤应力σz与表面应力σ0间的关系Fig.2 Relationships between soil stress σz and surface stress σ0 in a loading process

使用土壤固结仪对制备好的土壤样品进行单轴压缩实验，同时由土压力传感器监测因逐次加载(σ0)而产生的土壤应力(σz)(如图1a)，进而描述受压过程中土壤应力传递系数变化。将制备好的土壤样品放置于透水石中央，如图1b所示，土壤压力传感器内嵌于透水石圆心处。土壤压力传感器型号DZ-I，尺寸φ17 mm×7 mm，量程1 MPa[40]。为避免受压过程中传感器的拱效应，确保传感器与透水石上表面处于同一平面[39],另将直径为48 mm的加载板置于土壤样品的上表面，再开始实验。通过添加砝码使环刀中的土壤依次承受50、100、200、300、400、500 kPa的加载力，每2次加载间隔30 min使加载力全部施加于土壤样品，同时记录加载板下陷的位移ε(cm)[40]。在整个过程中，计算机数据采集系统会不间断的记录下土压力传感器监测到的土壤应力。需要注意的是该实验是一次性单向加载，并无循环加载卸载过程。

在实验前按照DAVE等[39]的方法自制土工膜液囊标定土压力传感器。根据Cassagrande 方法计算各参数土壤样品的先期固结压力[41-42]。利用SPSS Statistics 20.0统计软件做双因素(含水率、湿密度)方差分析，采用Duncan方法进行多重比较(α=0.05)。

图1 加载装置和监测系统Fig.1 Loading device and monitoring system1.土壤固结仪 2.测试系统 3.土壤样品 4.土压力传感器 5.传感器电缆 6.透水石

3 结果与分析

3.1 应力传递系数的计算

图2所示为重塑水稻土(含水率20%)和黄棕壤(含水率22%)在受压过程中土壤应力σz随表面应力σ0的变化。由图可知，σz与σ0间存在着相对稳定的线性关系(图2a湿密度为1.1、1.3、1.5 g/cm3时拟合曲线R2为0.958 7、0.970 5、0.933 1)，当土壤含水率、湿密度、土壤类型发生改变时，线性关系同样稳定。这意味着对于给定的土壤，在其加载过程中应力传递系数(σz/σ0)始终保持恒定，并同时受到含水率和湿密度的影响。因此应力传递系数在数值上等于σz-σ0拟合直线的斜率，图中3种湿密度水稻土的应力传递系数分别为0.82、0.69、0.60，黄棕壤的应力传递系数分别为0.61、0.62、0.58。

3.2 土壤参数对应力传递系数的影响

图3为土壤含水率与湿密度对应力传递系数的综合影响，从图中可以看出含水率对土壤的应力传递系数影响显著。含水率越大土壤的应力传递系数越大。随着土壤湿密度的变化，应力传递系数也随之变化，但变化规律不显著。应力传递系数作为一个稳定可测的土壤应力传递性能参数，含水率的增大会导致土壤应力传递系数增大，这意味着在受压过程中，高含水率的土壤条件更有利于应力往土壤底层传递。这一结果与大多数研究结论相吻合[19,24,31]。LAMANDÉ等[31]针对结构性土壤研究后提出，表面应力恒定时增加土壤含水率，从底层土壤中会探测到明显增大的土壤应力。SAFFIH-HDADI等[37]基于重塑土的实验表明，含水率越高，土壤越容易被压实。ARVIDSSON等[19]和DÉFOSSEZ等[43]发现土壤中的含水率较高时，受压后土壤的形变较大。

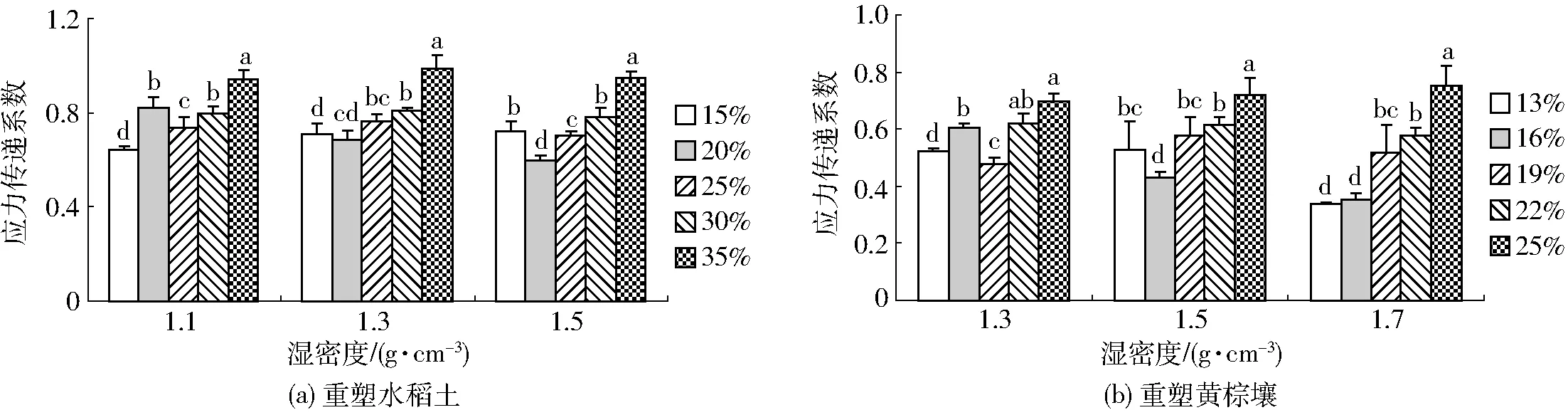
图3 土壤含水率和湿密度对应力传递系数的影响Fig.3 Effects of soil water content and bulk density on STC

建立应力传递系数与土壤初始干密度的关系，发现两者之间呈明显的负相关关系(图4)。土壤初始干密度越小，应力越容易通过土体传递到更深的位置[26,44]，即初始干密度越小，土壤的应力传递效率越高。SMITH等[24]认为在土壤受压时初始干密度是影响土壤形变和可承压能力的重要因素，初始干密度较大的土壤不易被压实[32]。

应力传递系数与土壤先期固结压力间也表现为负相关变化，说明先期固结压力是影响土壤的应力传递效率的重要参数。这与SÖHNE[25]、HORN等[28]、RÜCKNAGEL等[23]的结果相一致。运用HORN等[28]的理论可以计算出先期固结压力较大时，土壤应力较小。然而也有研究表明在先期固结压力完全不同的2种土壤中，土壤应力的传递并没有发现不同[45]。这是因为土壤的先期固结压力σp反映了土壤在前期所受的最大压实应力，被称为阈值应力[41-42]。如果随后施加的压力低于该阈值，土壤将不发生进一步压实，但高于该阈值的应力过程就会造成土壤进一步的压实[42]，即先期固结压力是阈值参数而并非定量土壤应力传递的过程参数。

图4 土壤初始干密度对应力传递系数的影响Fig.4 Effects of initial soil dry bulk density on STC

从理论上讲，应力传递系数在数值上是小于1的参数，但在图3a、图4a和图5a中可以发现应力传递系数存在大于1的情况，该情况主要出现在含水率为35%的水稻土条件下。在该状态下土壤含水率接近液限，受压后整体流动，加载力几乎全部作用于底部传感器处。同时因使用自制液囊标定土压力传感器，土工膜较差的收缩性能导致标定结果出现较小偏差。所有的应力传递系数数值均是基于这一标定结果获得，因此在运用应力传递系数的过程中需要更准确地对土压力传感器进行标定。

图5 先期固结压力σp与应力传递系数间的关系Fig.5 Relationships between precompression stress σp and STC

尽管应力传递系数与土壤物理参数(含水率、干密度、先期固结压力)间有着良好、可重复的稳定关系，但本实验是基于室内有限的重塑土实验，还需要更进一步在田间结构性土壤中验证应力传递系数理论的可靠性。然而从图3中可以发现，土壤湿密度、含水率对应力传递系数影响显著但缺乏规律性，从图4、图5中同样可以看出应力传递系数与干密度、先期固结压力间关系密切但并无规律可循。这是因为应力传递系数是土壤环境对土壤应力传递性能影响的综合体现(如含水率、干密度、先期固结压力、粘结力和土壤水势等)，解释其随土壤环境的变化规律需要更综合全面地探讨土壤环境参数(非单一物理参数)对土壤应力传递的影响。

3.3 通过应力传递系数计算集中系数ν

由以上结果可知，应力传递系数确实受土壤环境的影响。通过公式(5)计算所得不同含水率、湿密度土壤状态的集中系数如表2所示。从表2可以看出，集中系数随着土壤含水率的增大而增大，但随

湿密度的变化趋势却不明朗。在以往的众多研究中，关于集中系数的取值说法不一[12,25-31]，然而这些不一致的观点却都能在表2中得到体现。经Frölich和Söhne修正后，分析模型广泛地应用于土壤机械压实领域，然而集中系数引入时取值的局限性限制了该模型的推广[46]。表2展示了基于应力传递系数理论定量集中系数ν的方法。根据计算结果，集中系数取值范围1.20～12.39，与已有集中系数的取值范围2.0～14.3极为相近[12, 27-31]。同时如表2所示，集中系数ν经应力传递系数直接与土壤环境参数(物理参数)关联，不再是根据土壤坚硬程度取值。同样硬度的土壤既可以是高含水率、高密度的状态，也可以是低含水率、低密度状态，然而在表1中可以看出这2种状态下土壤集中系数间存在较大的差别。

表2 通过应力传递系数计算得到的集中系数(R=50 mm, z=50 mm)

表中数据为z=50 mm时集中系数的取值，随着轮胎-土壤接触面正下方z点深度的变化，集中系数也会随之变化。需要注意的是除了公式(5)中z的取值，变化的还有土壤应力传递系数(σz/σ0)的取值。对于环境参数(含水率、湿密度、土壤强度等)固定的土壤，z(土壤厚度)是影响σz的重要因素。因此在测量土壤应力传递系数时需要将土壤厚度加以更改。如z=100 mm时，实验测量时的土壤样品厚度应该100 mm。使用公式(5)计算集中系数的前提是土壤在受压过程中表现为弹塑性变形，LAMANDÉ等[34]认为土壤形变越大集中系数ν取值越大。在本文实验中加载板下陷位移小于土壤样品厚度的10%，因此该因素可忽略不计。

国内已有的压实研究成果，成功地为农业机械-土壤相互作用提供了可视化数据，然而土壤压实机理的未知，系统评价土壤压实模型的缺失，依然是无法形成一套有效消减土壤压实技术体系的主要障碍[14]。土壤压实的过程主要分为3步[18]：在轮胎-土壤交互的过程中应力施加到土壤表面；应力在土壤内部传递；土壤应力引起了土壤结构的变化。本文针对的主要是“应力在土壤内部传递”这一过程。使用分析模型预测土壤应力的困扰在于确定集中系数[12]，应力传递系数的提出，在完善分析模型的同时，将土壤应力与土壤环境间的关系清晰化。通过研究土壤环境参数对应力传递系数的影响，可以进一步明确哪些土壤环境参数对土壤应力的传递影响较大，土壤应力又是如何随某一土壤环境参数(如含水率、密度、入渗率、导水率、导气率等)的变化而变化。这一土壤压实研究方法的优化，可以进一步揭示压实机理，明确压实过程，为消减土壤压实提供理论基础。

4 结论

(1)本文从理论出发，基于传统的土壤应力分析模型，提出了能够代表土壤环境自身应力传递效率的应力传递系数，并用实验的方法证明，该参数稳定可测。

(2)应力传递系数受土壤环境的综合影响，与含水率、干密度、先期固结压力等之间存在明显的相关性。

(3)集中系数是使用分析模型预测土壤应力的关键参数，应力传递系数为准确定量集中系数提供了一个科学的方法。优化了土壤压实研究方法，为消减土壤压实提供了技术基础。

1 刘任先. 农业土壤压实应变与流动特性的测试方法——精确喷印网格法[J]. 北京农业机械化学院学报, 1983(1): 103-107. LIU Renxian. The accurate sprayed-Grid method for measuring soil compaction and plastic flow [J]. Beijing Agricultural Mechanization College, 1983(1): 103-107.(in Chinese)

2 陈浩，杨亚莉. 土壤压实模型分析[J]. 农机化研究, 2012, 34(1): 46-50. CHEN Hao，YANG Yali. Analysis of soil compaction models [J]. Journal of Agricultural Mechanization Research, 2012, 34(1): 46-50.(in Chinese)

3 张家励，傅潍坊. 土壤压实特性及其在农业生产中的应用[J]. 农业工程学报, 1995,11(2): 17-20. ZHANG Jiali，FU Weifang. The soil compactive characteristics and their application in agriculture production [J]. Transactions of the CSAE, 1995,11(2): 17-20.(in Chinese)

4 KELLER T, BERLI M, RUIZ S, et al. Transmission of vertical soil stress under agricultural tyres: comparing measurements with simulations[J]. Soil and Tillage Research, 2014, 140: 106-117.

5 SOANE B D, VAN OUWERKERK C. Implications of soil compaction in crop production for the quality of the environment[J]. Soil and Tillage Research, 1995, 35(1-2): 5-22.

6 MARI G R, JI C, ZHOU J. Effect of different types of tractor traffic on soil physical properties and yield of winter wheat[J]. Transactions of the CSAE, 2007,23(10): 132-140.

7 迟仁立，左淑珍，夏平，等. 不同程度压实对土壤理化性状及作物生育产量的影响[J]. 农业工程学报, 2001, 17(6): 39-43. CHI Renli，ZUO Shuzhen，XIA Ping，et al. Effects of different level compaction on the physicochemical characteristerics of soil and crop growth [J]. Transactions of the CSAE, 2001, 17(6): 39-43.(in Chinese)

8 孙忠英，李宝筏. 农业机器行走装置对土壤压实作用的研究[J]. 农业机械学报, 1998, 29(3): 172-174. SUN Zhongying，LI Baofa. Effect of agricultural machine walking device on soil compaction [J].Transactions of the Chinese Society for Agricultural Machinery, 1998, 29(3): 172-174.(in Chinese)

9 张兴义，隋跃宇. 土壤压实对农作物影响概述[J]. 农业机械学报, 2005, 36(10): 161-164. ZHANG Xingyi, SUI Yueyu. Summarization on the effect of soil compaction on crops[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005,36(10):161-164. (in Chinese)

10 NAWAZ M F, BOURRIÉ G, TROLARD F. Soil compaction impact and modelling. A review[J]. Agronomy for Sustainable Development, 2012, 33(2): 291-309.

11 李汝莘，林成厚，高焕文，等. 小四轮拖拉机土壤压实的研究[J]. 农业机械学报, 2002, 33(1): 126-129.

12 KELLER T, LAMANDÉ M. Challenges in the development of analytical soil compaction models[J]. Soil and Tillage Research, 2010, 111(1): 54-64.

13 DEFOSSEZ P, RICHAD G. Models of soil compaction due to traffic and their evaluation[J]. Soil and Tillage Research, 2002, 67(1): 41-64.

14 王宪良，王庆杰，李洪文，等. 农业机械土壤压实研究方法现状[J]. 热带农业科学, 2015,35(6): 72-76. WANG Xianliang，WANG Qingjie，LI Hongwen，et al. Current research status of soil compaction by agriculture machinery [J]. Chinese Journal of Tropical Agriculture, 2015,35(6): 72-76.(in Chinese)

15 ABU-HAMDEH N H, REEDER R C. Measuring and predicting stress distribution under tractive devices in undisturbed soils[J]. Biosystems Engineering, 2003, 85(4): 493-502.

16 李汝莘，宋洪波，高焕文. 小型拖拉机土壤压实的有限元预测[J]. 农业工程学报, 2001, 17(4): 66-69. LI Ruxin，SONG Hongbo，GAO Huanwen. Prediction of soil compaction by small tractor using finite element method [J]. Transactions of the CSAE, 2001, 17(4): 66-69.(in Chinese)

17 赵振家，邹猛，薛龙，等. 压实对土壤应力分布的影响仿真分析[J/OL]. 农业机械学报, 2012, 43(增刊): 311-313.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=2012s63&journal_id=jcsam.DOI：10.6041/j.issn.1000-1298.2012.S0.063. ZHAO Zhenjia，ZOU Meng，XUE Long，et al. Simulation analysis of effect of compaction on soil stress distribution [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(Supp.): 311-313.(in Chinese)

18 O’SULLIVAN M F, HENSHALL J K, DICKSON J W. A simplified method for estimating soil compaction[J]. Soil and Tillage Research, 1999, 49(4): 325-335.

19 ARVIDSSON J, TRAUNTNER A, VAN DEN AKKER J J H, et al. Subsoil compaction caused by heavy sugarbeet harvesters in southern Sweden: II. soil displacement during wheeling and model computations of compaction[J]. Soil and Tillage Research, 2001, 60(1-2): 79-89.

20 TRAUTNER A. On soil behaviour during field traffic[D]. Uppsala: Sveriges Lantbruksuniv., 2003.

21 VAN DEN AKKER J J H. SOCOMO: a soil compaction model to calculate soil stresses and the subsoil carrying capacity[J]. Soil and Tillage Research, 2004, 79(1): 113-127.

22 KELLER T, DÉFOSSEZ P, WEISSKONPF P, et al. SoilFlex: a model for prediction of soil stresses and soil compaction due to agricultural field traffic including a synthesis of analytical approaches[J]. Soil and Tillage Research, 2007, 93(2): 391-411.

23 RÜCKNAGEL J, HOFMANN B, DEUMELANDT P, et al. Indicator based assessment of the soil compaction risk at arable sites using the model REPRO[J]. Ecological Indicators, 2015, 52: 341-352.

24 SMITH R, ELLIES A, HORN R. Modified Boussinesq’s equations for nonuniform tire loading[J]. Journal of Terramechanics, 2000, 37(4): 207-222.

25 SÖHNE W. Distribution of pressure in the soil and soil deformation under tractor tires[J]. Grundl. Landtech, 1953, 5: 49-59.

26 RAM R B. Pressure measurement in the soil under the load[J]. Soil and Tillage Research, 1984, 4(2): 137-145.

28 HORN R, FLEIGE H. A method for assessing the impact of load on mechanical stability and on physical properties of soils[J]. Soil and Tillage Research, 2003, 73(1-2): 89-99.

29 LAMANDÉ M, SCHJØNNING P. Transmission of vertical stress in a real soil profile. Part I: site description, evaluation of the Söhne model, and the effect of topsoil tillage[J]. Soil and Tillage Research, 2011, 114(2): 57-70.

30 LAMANDÉ M, SCHJØNNING P. Transmission of vertical stress in a real soil profile. Part II: effect of tyre size, inflation pressure and wheel load[J]. Soil and Tillage Research, 2011, 114(2): 71-77.

31 LAMANDÉ M, SCHJØNNING P. Transmission of vertical stress in a real soil profile. Part III: effect of soil water content[J]. Soil and Tillage Research, 2011, 114(2): 78-85.

32 JONES R J A, SPOOR G, THOMASSON A J. Vulnerability of subsoils in Europe to compaction: a preliminary analysis[J]. Soil and Tillage Research, 2003, 73(1-2): 131-143.

33 KELLER T, ARVIDSSON J. Technical solutions to reduce the risk of subsoil compaction: effects of dual wheels, tandem wheels and tyre inflation pressure on stress propagation in soil[J]. Soil and Tillage Research, 2004, 79(2): 191-205.

34 LAMANDÉ M, SCHJØNNING P, TØGERSEN F A. Mechanical behaviour of an undisturbed soil subjected to loadings: effects of load and contact area[J]. Soil and Tillage Research, 2007, 97(1): 91-106.

35 柏建彩，丁启朔，陈青春，等. 农田原状土壤压实测试系统的设计及操作方法[J]. 江苏农业科学, 2015(1): 368-370. BO Jiancai，DING Qishuo，CHEN Qingchun，et al. Undisturbed soil compaction test system design and operation method in farmland [J]. Jiangsu Agricultural Sciences, 2015(1): 368-370.(in Chinese)

36 汪攀峰，丁启朔. 黏土单层击实试验与制样因子研究[J]. 岩土力学, 2010, 31(6): 1797-1802. WANG Panfeng，DING Qishuo. Study of dynamic compaction of monolayer cohesive soil and factors for remolded soil [J]. Rock and Soil Mechanics, 2010, 31(6): 1797-1802.(in Chinese)

37 SAFFIH-HDADI K, DÉFOSSEZ P, RICHAD G, et al. A method for predicting soil susceptibility to the compaction of surface layers as a function of water content and bulk density[J]. Soil and Tillage Research, 2009, 105(1): 96-103.

38 TAGAR A, JI C, DING Q, et al. Soil failure patterns and draft as influenced by consistency limits: an evaluation of the remolded soil cutting test[J]. Soil and Tillage Research, 2014, 137: 58-66.

39 DAVE T N, DASAKA S M. In-house calibration of pressure transducers and effect of material thickness[J]. Geomechanics & Engineering, 2013, 5(1): 1-15.

40 THOMAS K, JOHAN A, PER S, et al. In situ subsoil stress-strain behavior in relation to soil precompression stress[J]. Soil Science, 2012, 177(8): 490-497.

41 AJAYI A E, DIAS JUNIOR M D S, CURI N, et al. Strength attributes and compaction susceptibility of Brazilian Latosols[J]. Soil and Tillage Research, 2009, 105(1): 122-127.

42 李春林，丁启朔，陈青春. 水稻土的先期固结压力测定与分析[J]. 农业工程学报, 2010, 26(8): 141-144. LI Chunlin，DING Qishuo，CHEN Qingchun. Measurement and analysis of precompression stress of soil in rice field [J]. Transactions of the CSAE, 2010, 26(8): 141-144.(in Chinese)

43 DÉFOSSEZ P, RICHAD G, BOIZARD H, et al. Modeling change in soil compaction due to agricultural traffic as function of soil water content[J]. Geoderma, 2003, 116(1-2): 89-105.

44 SMITH D L O. Compaction by wheels: a numerical model for agricultural soils[J]. European Journal of Soil Science, 1985, 36(4): 621-632.

45 ZINK A, FLEIGE H, HORN R. Load risks of subsoil compaction and depths of stress propagation in arable luvisols[J]. Soil Science Society of America Journal, 2010, 74(5): 1733-1742.

46 SELVADURAI A P S. On Fröhlich’s solution for Boussinesq’s problem[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2014, 38(9): 925-934.

Soil Stress Transmission Coefficient Based on Compaction Analytical Model

HE Tingfeng1CONG Wenjie1BELAL Eisa Adam1,2DING Qishuo1YANG Yanshan1HUO Lianfei1

(1.CollegeofEngineering,NanjingAgriculturalUniversity,Nanjing210031,China2.DepartmentofAgriculturalEngineering,ZalingeiUniversity,Zalingei06,Sudan)

Predicting soil stress with analytical models requires proper selection of the models’ concentration factor. But due to the insufficient knowledge about the effects of soil conditions on stress transmission, little is known about how the concentration factor varies with soil states and loading conditions. The function of the concentration factor was transformed and a dimensionless factorσz/σ0standing for soil-induced attenuation on the stress transmission was defined as the soil stress transmission coefficient and is denoted as STC. Since soil stress transmission property is affected by soil states and loading conditions, a modified oedometer testing setup with a soil stress sensor was used to evaluate controlled soil properties on STCs. Totally 30 soil states were tested by controlling soil water contents and bulk densities based on different soil styles. Correlation analysis was performed between measured STCs and soil state parameters, i.e. water content, bulk density and soil strength. The highly linear correlation between soil stress and applied surface stress indicated a stable STC for each particular soil state. STC was also found both linearly decreased with dry bulk density and precompression stress. The back-calculation of concentration factor from measured STCs illustrated that the proposed solution for soil stress transmission provided a means to define concentration factor for each soil state with measured result. Concentration factor varied from 1.20 to 12.39, being in agreement with the past reports. And the detail of how the concentration factor was affected by the changed states of soils was provided.

soil compaction; analytical model; concentration factor; soil condition; stress transmission coefficient

10.6041/j.issn.1000-1298.2017.06.007

2016-10-23

2016-12-11

国家自然科学基金项目(41371238)

贺亭峰(1992—)，男，博士生，主要从事土壤压实力学研究，E-mail： hetingfeng_543364@126.com

丁启朔(1968—)，男，教授，博士生导师，主要从事土壤耕作力学和压实力学研究，E-mail： qsding@njau.edu.cn

S152.9

A

1000-1298(2017)06-0059-07