大跨度PC连续刚构桥徐变预测模型
2017-06-26张亮亮曾泽润何建宏
张亮亮+曾泽润+何建宏


摘要:为了能准确预测混凝土收缩徐变,提出了一系列徐变预测模型,但传统的徐变理论研究主要是针对普通混凝土进行的,所提出的徐变模型并不能完全适用于高强混凝土。对各徐变预测模型进行分析比较,最终参考了日本混凝土示方书建议模型,并在高强混凝土徐变试验的基础上,提出了一个适用于高强混凝土的徐变预测模型。基于Abaqus平台,使用Python语言进行二次开发,定义了修正模型的徐变规律,并采用修正后的模型计算牛角坪大桥的徐变应变。结果表明,修正模型的精度,能很好的满足工程需求。
关键词:高强混凝土;连续刚构桥;预测模型;Python脚本
中图分类号:U441文献标志码:A文章编号:16744764(2017)03002807
Abstract:Nowadays all the existed prediction models around the world are only suitable for ordinary concrete with a strength lower than C40 or lightweight aggregate concrete with a strength under C30, however, there exists no prediction model for high strength concrete structures. Through the analysis and comparison of each creep prediction model, this paper concludes with reference to the proposed model of Japanese Concrete Codes. On the basis of creep test of high strength concrete, a creep prediction model for high strength concrete is proposed.Based on Abaqus Scriping Interface, new user's material properties that fitted Modified Model were created by Python. By comparing results of calculation and test data, a rule of creeps progress was obtained.
Keywords:Highstrength concrete; continuous rigid frame bridge; prediction model; python script
跨中挠度过大、主体截面出现裂缝是大型混凝土桥梁在运营过程中不可避免的问题。这些问题会随着时间而不断加剧,这不仅会影响到桥梁的正常使用,且可能会引发桥梁事故。大量研究及工程经验表明,收缩徐变是产生上述问题的主要影响因素之一。
长期以来,各国的研究者均对混凝土徐变开展过理论研究[13],以减少徐变所造成的安全隐患。为描述徐变发展情况,各国提出了诸多预测模型。如欧洲的CEBFIP模型,有1978和1990两个版本,中国主要参考CEBFIP 1978模型,美国的ACI209模型,此外,应用较为广泛的还有BS系列[5],BP系列,GZ(1993),GL2000模型,还有日本土木建筑学会提出的建议模型[6] 。以当前中国混凝土的发展情况来看,以往的计算模型已不能够满足工程上的要求,因此,加大这方面的研究工作的力度,提出符合中国国情的徐变计算模型是非常有必要的。此前已进行了与牛角坪大桥相同的高强混凝土试验,所用混凝土配合比与牛角坪大桥的相同,基于所试验所得到的数据,参考日本混凝土示方书的建议模型,最终给出了一个更适用于牛角坪大桥的高强混凝土徐变修正模型。本文利用Python Script Language通过Abaqus Scripting Interface对Abaqus进行二次开发,通过Finite Element Methodology(FEM)建模[7],模拟了修正模型的徐变发展历程,并模拟ACI209(1982)模型作为比较。总结分析所得到的模拟结果,对比3组数据,即修正模型和ACI209(1982)模型的模拟结果与工程实测数据,可以发现本文所提出的修正模型与之更为相符,因此可以认为,该模型能够满足牛角坪大桥的工程要求。
1混凝土徐变预测模型
1.1混凝土收缩徐变的影响因素
学者们对混凝土收缩徐变进行了诸多理论研究,其中相当部分的研究工作是围绕影响混凝土收缩徐变的因素展开的[8~9]。一般认为,对混凝土收缩徐变影响最大的主要有,混凝土自身材料的性质,其所采用的制作工艺,加载过程和受力状态,以及所处的工作环境等[10]。
1.3不同预测模型对比分析
混凝土徐变模型多种多样,其预测精度也各有不同,因此需要进行模型的精度评估。现广泛采用的B3变异系数法是基于B3模型提出的,其表示的是模型的计算值与各徐变数据的相对偏差的总和。显然其值越小,则所对应的预测模型越为准确。
文献[16]选用了来自17个国家约15 000个徐变数据点,对CEBFIP1978等模型进行了评估和检验[1113],按照不同的应力水平以及不同的加载龄期,计算得到各模型的变异系数,各模型的计算精度见表1。从表1可以看出,GL2000最為精确,RILEMB3和日本的混凝土规范表现良好, ACI209(82)模型以及CEBFIP1978模型的误差最大。
2对桥用混凝土徐变预测模型的修正
2.1桥用高强混凝土收缩徐变试验
为得到牛角坪大桥桥用高强混凝土收缩徐变特性,故需进行收缩徐变试验,以期在试验的基础上提出适用于此类高强混凝土的修正模型。
收缩徐变试验在恒温恒湿试验室中进行,所采用的高强混凝土配合比如表2所示,各材料配比与牛角坪大桥一致。
徐变试验共有两个试件,即100 mm×100 mm×300 mm,编号为1#,100 mm×100 mm×150 mm,编号为2#。另制作3个尺寸为150 mm×150 mm×150 mm的立方体试件,用于混凝土强度的测量;制作3个尺寸为100 mm×100 mm×300 mm棱柱体试件,用于弹性模量的测量。试件在拆模后立即送入标准养护室分别养护到3、7、28 d,然后移入至恒温恒湿试验室。在标准养护条件下进行测定,结果如表3所示。
2.2加载与测试
本试验采用JSFXVI/31.54(100t)型高精度伺服液压系统进行加压。为了观察混凝土的变形情况,于混凝土试件内部预埋电阻式应变计。
由于温度及湿度等养护条件对徐变的影响很大,为消除此类因素的影响,在试验中,在试件成型后,将试件代模移至恒温恒湿试验室中进行养护至预定龄期,其中温度控制为20±2 ℃,相对湿度为80%左右。
根据ACI 209关于混凝土试验的建议,同时考虑到,在实际工程中,预应力混凝土的张拉时间一般为混凝土成型后的5~7 d左右,因此本试验选择养护龄期 7 d后进行加载。为保证试验设备在正常工作状态下工作,且保证加载应力与混凝土徐变变形呈线性关系,本文选用应力比(混凝土试件所受应力与混凝土强度之比)为0.33,即加载应力为22.94 MPa,一方面是参考了国内外的相关试验,其加载应力水平多在30%~40%的范围,另外,从实际工程的角度,大多大跨预应力混凝土结构的正常工作环境,其应力一般是小于混凝土强度的40%,这也与我国规范所规定的加载应力相符。
试验试件在进行标准养护7天后移入恒温恒湿试验室中进行加载,采用千分表对试件的变形进行测量,所得初始测量值即为试件在徐变荷载作用下的初始变形值。此后,在徐变荷载作用下,按一定的时间间隔对混凝土试件的变形值进行测量。根据试验测得的变形数据按式(1)即可计算出各时间点的混凝土徐变系数。
2.3试验结果
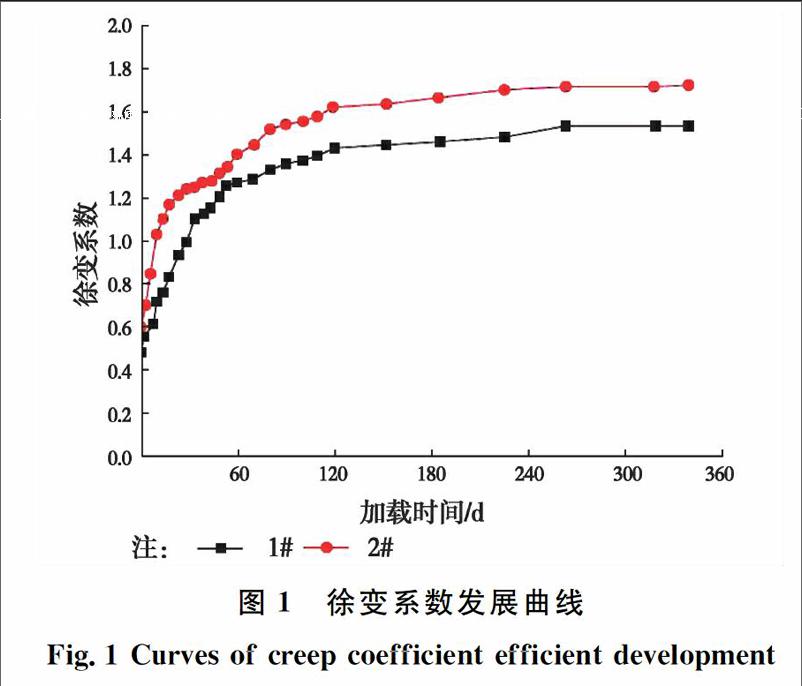
2个试件的徐变系数发展情况如图1所示。由试验结果可知,徐变的早期发展速率较快,1#试件在28 d龄期的徐变系数为0.843,2#试件为0.998,均约占最终徐变发展的60%。在30~240 d间,试件的徐变仍平稳增长,但发展速率逐渐减缓,两试件在250 d的徐变系数分别为1.481及1.684。在240 d之后,试件的徐变发展均趋于迟缓。
早龄期的混凝土徐变发展较快,这是由于其水化反应未充分,混凝土内部尚有较多的空隙及还未水化的凝胶粒子,水分及部分流体在徐变荷载的作用下会发生流动,而早龄期较其他时期更易发生流动,故徐变发展速率较快。而随着龄期增大,混凝土内部的水化反应逐步发展,混凝土逐渐发展密实,从而减少了水分及流体的流动,故徐变发展速率较为缓慢。
2.4修正模型的提出
日本混凝土示方书考虑的因素较为充分,从上文的评估结果来看,其具有相当的精度。本文以该模型作为修正的基础模型,利用狄利克雷级数形式,结合徐变试验数据对其进行修正[14] ,经修正的徐变系数表达式为
式中:t为混凝土龄期;t0为养护龄期;n为级数的项数;αi(t0)为线性组合系数,它是t0的函数;λi为龄期的调整系数。各系数均通过对试验数据的拟合所得,其值如表4所示。
3牛角坪大桥长期徐变变形实测
3.1牛角坪大桥概况
牛角坪大桥为预应力混凝土连续刚构桥,其跨径布置为100+192+100 m。大桥梁截面为单箱单室变高度变截面箱梁,混凝土实际强度为65 MPa。梁体设置三向预应力,其中纵、横向均采用φ15.2 mm的高强度低松弛钢绞线,竖向采用φ32 mmPSB830螺纹钢筋。
3.2应变测量布置
自2011年7月起,历时约为3 a,对牛角坪大桥进行了长期的观测工作,采集了包括徐变效应在内的大量实测数据,本文提取了7个时间点:2011年7月、2011年9月、2011年12月、2012年3月、2012年7月、2012年9月、2012年12月的实测数据进行分析。根据徐变在早期增长较快,后期逐渐平缓的发展规律,故在实际的测量工作中,测量频率随时间而逐步减少,每次的观测时长为3 d左右,先后对其进行10次左右的实测工作。该桥取7个控制截面进行观测,具体布置位置如图1所示,考虑到牛角坪大橋为三跨刚构桥,从工程角度考虑,选取了截面面积最小及最大处,即合龙段(S1,S7),以及左右两跨根部截面(S3,S5)。布置了边跨及主跨跨中位置(S2,S4,S6)。截面应变采用震弦式传感器进行测量,相应的测点布置如图3。
3.3应变测量数据统计与分析
根据前方的测量方案,通常测量的频率为每10 min一次,每日持续测量时间为20 h,即涵盖了一日之中的大部分时间。测试的结果即通过将所测取的数组数据求均值获得。由前所述的徐变发展规律,徐变的是一种正增长,其增长不为负,即徐变不会出现降低的情况。实测结果如下图所示,图中每条应变曲线均呈波浪型的拆线式发展。这似乎与常识相左。会呈现这种结果,是因为测量是以季为单位,故每次测量时所处的外界条件不尽相同,包括温度以及湿度等条件,这些外部条件是影响徐变的主要因素之一。通过对比相同季度的测量数据,既可验证这一点。为消除外温度等因素的影响,可采用不同年份、同一时期的测量数据对比分析。
1)图4给出了左边跨合龙截面(S1)的部分具有代表性测点的实测结果曲线。根据取两年中相同季度数据进行对比分析的原则,同比两年中7月、9月、12月的测试结果,可以总结出一定的规律。即在左边跨合龙截面处,各测点的应变均处于一种缓慢的增长状态。因此可以推测,牛角坪大桥的徐变将会持续增长,但这种增长的将在3~4 a内逐渐处于稳定的状态。
从图5可以看出,在矮墩根部截面处,上下缘应变的增长呈现出了差异。对比P5测点(位于下缘)与P1测点(位于上缘)在两年中7月、9月、12月的测试结果,P5测点应变增长分别为75、64、61 με,而P1测点则为20με,18με,15με。这即验证了徐变在早期增长较快,后期逐渐平缓的发展规律,同时也说明,在同一截面中,下缘的应变增加速率会稍快。
有限元模拟二次开发
Abaqus中虽提供了3种徐变律(Creep Principles),但对于混凝土,特别是大跨度预应力混凝土,这3种模型并不适用。本文利用Python语言进行二次开发,定义了前文所提出的徐变预测模型,为作对比分析,定义了ACI 209 (1982)模型[15] ,通過有限元仿真计算,对结果进行总结分析。
4.1牛角坪大桥有限元分析
本次计算中使用的单元为ABAQUS标准单元库中编号为C31H的梁单元。由于线性单元求解运算并不复杂,故在计算时没有采用减缩积分,以避免人为提升结构的总体刚度。
4.2实测结果与计算结果对比分析
根据所编写的ABAQUS脚本构建实桥模型,用上述两种模型对徐变值进行预测。根据气象资料,当地湿度在全年之中的波动不大,对预测值的影响很小,故统一取平均湿度70%进行计算。实测数据受季节影响很大,主要是温度的影响,故采用温度补偿的方式对实测数据进行修正。即计算该桥合龙时与实测时的温差,在此基础上得出相应的温度对于应变测量结果的影响系数,以修正实测数据。考虑了实测补偿值的实测数据,减小了温度对徐变计算的影响,使得其呈现出更好的发展规律,因而与模拟计算的结果更具可比性。根据所得的分析结果绘制成图,S1截面及S5截面的结果如图6所示。
对比两个截面的分析结果,可知:
1) 从应变趋势上来看,美国ACI209(1982)模型的表现尚可,但应变值总体上会大于实际观测值,这主要是应该该模型没有根据实际情况,对混凝土强度进行调整。故可以认为,ACI209(1982)模型可以用来对混凝土徐变做粗略的估计,其所得的徐变应变值较为精确,但存在波动。
2) 从图7可以看出,不论实测数据还是预测值,各曲线均呈对数曲线的形式。即前期增长迅速,在3个月以内,混凝土的徐变既已发展了一半以上,而后期的曲线趋于平缓,各截面均在1 a以内完成大部分的徐变应变。
本文总结了预测模型的预测值与实测数据的偏差情况,部分较有代表性的结果见表5。若预测值大于实测值,则其值为正,反之为负。可以发现,ACI209(1982)模型的表现存在较大的波动,而修正模型在除0#块以外的截面均表现良好。这主要是由于0#块与其他截面相比,其截面面积较大,因此使预测值产生了偏差。
5结论
1)依托于大跨刚构桥的实测,总结分析各组数据,证实了混凝土徐变的发展规律,即早期增长较快,后期发展速度放缓,直至趋于稳定。
2)基于Abaqus,利用Python进行仿真分析。由计算结果可以发现:桥用高性能预应力混凝土在一到三年以内完成大部分的徐变应变,而之后的徐变应变增长趋于平缓。这与普通混凝土的徐变发展规律相近。
3)在对高强混凝土徐变值的预测中,ACI209(1978)模型具有一定的精度,但准确性存在波动,故可用于粗略的徐变估计。而本文所提出的修正模型,在除0#块特异截面以外,各时段各截面的预测值均较为准确,可以满足工程上的需求。
参考文献:
[1] RANAIVOMANANA N, MULTON S, TURATSINZE A. Basic creep of concrete under compression, tension and bending [J]. Construction & Building Materials, 2013, 38(1):173180.
[2] 山本俊彦. 1366 コンクリートのクリープ?乾燥収縮予測式の比較[R]. 学術講演梗概集 2012(材料施工):731732.
YAMAMOTO Toshihiko. 1366 comparison of creep and shrinkage prediction models of concrete[R]. Summaries of Technical Papers of Annual Meeting 2012:731732. (in Japanese)
[3] 韩静云.粉煤灰对桥用高性能混凝土徐变性能影响的研究[D].重庆:重庆大学,2013.
HAN J Y. Study of the Influence of fly ash on the creep property of high performance concrete used in bridge[D]. Chongqing: Chongqing University,2013. (in Chinese)
[4] 公路钢筋混凝土及预应力混凝土桥涵设计规范:JTJ023—85[S].北京:人民交通出版社,1985.
Highway reinforced concrete and prestressed concrete bridge design specifications:JTJ02385[S]. Beijing: China Communications Press, 1985.
[5] 英国标准协会.BS8110《英国混凝土结构规范》[S].中国建筑科学研究院结构所规范室译,1993:191195.
British Standards Institution.BS8110 Structural use of concrete[S]. China Academy of Building Research Structures Standardized Room Translation, 1993:191195.
[6] 日本土木学会.コンクリート標準示方書「構造性能照査編」[S].东京. 2002.
Japan Society of Civil Engineers. Standard specification for concrete structure(Structural Performance Varification) [S]. Tokyo,2002. (in Japanese)
[7] 曹金凤,王旭春,孔亮.Python语言在Abaqus中的应用[M].北京:机械工业出版社,2011.7.
CAO J F, WANG X C, KONG L. Application of Python language in Abaqus[M]. Beijing: Machinery Industry Press, 2011. (in Chinese)
[8] 後藤忠広, 上原匠, 梅原秀哲. 1194 若材齢コンクリートのクリープ挙動に関する研究(マスコンクリート)[C]// コンクリート工学年次論文報告集, 1995, 17:11331138.
GOTO T,UEHARA T,UMEHARA H. 1194 Studies on Creep Behavior of Early Age Concrete[C]// Proceedings of the Japan Concrete Institute, 1995:11331138. (in Japanese)
[9] 橋場盛.コンクリートの時間依存性ひずみと構造物の設計手法に関する研究[R].京都大学,平成13年.
Hashiba Mori. Study on the design method of timedependent strain and structure of concrete[R]. Kyoto University, 2001. (in Japanese)
[10] GARDNER N J,LOCKMAN M J. Design provisions for drying shrinkage and creep of normalstrength concrete[J]. ACI Materials Journal, 2001,98(21):159167.
[11] 美国各州公路和运输工作者协会制订. 美国公路桥梁设计规范[M]., 辛济平,译. 人民交通出版社, 1998.
AASHTO. Guide specification and commentary for vessel collision design of highway bridges[M]. Xin Jiping translated. Beijing : China Communications Press, 1998.
[12] 千々和伸浩,石田哲也,前川宏一.コンクリートの微細空隙中の水分とPC橋の長期変位[J].橋梁と基礎,20111.
CHIJIWA N, ISHIDA T, MAEKAWA K.Effect of moisture in micro pores of the concrete on longterm deflection of prestressed concrete bridge[J]. Bridge and foundation engineering,20111. (in Japanese)
[13] 横道英雄.プレストレストコンクリート[M].鹿儿岛出版会,昭和58年9月:224230
YOKOMICHI H.Prestressed concrete [M]. Kagoshima publication board, 1983: 224230. (in Japanese)
[14] 张康.高墩大跨连续刚构桥长期变形研究[D].重庆大学,2013.
ZHANG K.Study on longterm deformation of longspan rigid frame bridges with high piers[D].Chongqing University,2013. (in Chinese)
[15] 张波.基于ABAQUS用户子程序的岩体非线性蠕变模型[J].土工基础,2012,26(2):5860.
ZHANG B. Incorporation of nonlinear rock mass creep constitutive model into finite element analysis using user subroutine[J].Soil Engineering and Foundation,2012,26(2):5860. (in Chinese)
[16] LAM J P. Evaluation of concrete shrinkage and creep prediction models[D]. San Jose State University. 2002.
(編辑胡玲)
