初中数学学习中分类讨论的应用

甘肃省陇南市武都区滨江学校 秦晓勇

分类讨论思想是初中数学中一种非常重要而且常见的思维。在每年的中考试题中，常常利用分类讨论来加大试卷的区分度，而且分类讨论思想与新课程改革中提出的培养学生的创新精神与探索精神是一致的。因此使学生养成分类讨论思想，并掌握一定的分类技巧以及常见题型的分类方法，形成一定的分类体系非常必要。

数学中，把问题划分为若干情况，然后逐一求解的过程叫作分类讨论，也称分情况讨论。 解答分类讨论问题的步骤是：

首先，确定讨论对象以及所讨论的对象的全体范围；

其次，确定分类标准，进行合理分类，再对所分情况进行求解，获取阶段性结果；

最后，进行归纳小结，综合得出结论。

现在，把初中数学教学中分类讨论的类型归纳如下：

一、由问题中分类定义的概念和性质而引起的分类讨论

例 若a，b为非零实数，代数式的所有可能的值有（ ）

A 2个 B 3个 C 4个 D 无数个

解析：根据题意，按a，b的符号，分4种情况讨论；每种情况下，利用绝对值的性质去掉绝对值，求出代数式的值；然后综合几个结果，得出结论。

解：根据题意，按a，b的符号，分4种情况讨论：

①a＞0，b＞0时，原式＋1＋1=3

②a＞0，b＜0时，原式=1－1－1=－1

③a＜0，b＞0时，原式=-1＋1－1=－1

④a＜0，b＜0时，原式=－1－1＋1=－1

综上所述，共两种结果，故选A。

二、由问题中参数的不同取值引起的分类讨论

例题1：已知关于x的方程(k2－1)x2－2(k＋1)x＋1＝0有实数根，求k的取值范围。

解析：因为k出现在二次项系数，所以当k2－1=0时，－2(k＋1)≠0此方程为一元一次方程，一定有实数根。当k2－1≠0时，此方程是一元二次方程，方程有实数根，根据根的判别式△≥0求k的取值范围。因此分两种情况进行讨论。

解：（1）k2-1=0，－2(k＋1)≠0即k=1时，为一元一次方程，一定有实数根；

（2）k2－1≠0，即k≠±1时，此方程为一元二次方程

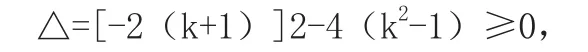
解得k≥-1.

综上可得k＞-1.

例题2：误解，求a=( )

解：去分母，得：

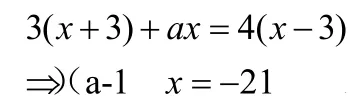
由已知或或a=0

猜想：把“无解”改为“有增根”如何解？ a=8或a=-6

例题3：已知方程有实数根，求m的取值范围。

（1）当m2=0时，即m=0时，方程为一元一次方程x+1=0，有实数根x=-1

（2）当m2≠0时，方程为一元二次方程，根据有实数根的条件得：

∆=即，且m2≠0

综（1）（2）得，

常见病症：（很多同学会从（2）直接开始而且会忽略的条件）

总结：字母系数的取值范围是否要讨论，要看清题目的条件。一般设置问题的方式有两种（1）前置式，即“二次方程”；（2）后置式，即“两实数根”。这都是表明是二次方程，不需要讨论，但切不可忽视二次项系数不为零的要求，本题是根据二次项系数是否为零进行讨论的。

例题4：当m是什么整数时，关于x的一元二次方程与的根都是整数。

解：因为是一元二次方程，所以二次项系数不为0，即解得：m≤1

同理，解得且又因为m为整数∴m取-1或1

（1）当m=—1时，第一个方程的根为不是整数，所以m=—1舍去。

（2）当m=1时，方程1、2的根均为整数，所以m=1.

练习：已知关于x的一元二次方程有实数根，则m的取值范围是：

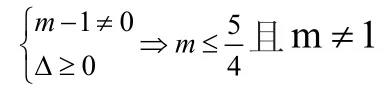
三、三角形、圆等几何图形相关量求解的分类讨论问题

例题1：方程x2-9x+18=0的两个根是等腰三角形的底和腰，则这个三角形的周长为（ ）

A 12 B 12或15

C 15 D 不能确定

例题2：（2011武汉）三角形一边长AB为13cm，另一边AC为15cm，BC上的高为12cm,求此三角形的面积。（54或84）

例题3：一条绳子对折后成图A、B, A.B上一点C，且有BC=2AC,将其从C点剪断，得到的线段中最长的一段为40cm,请问这条绳子的长度为：60cm或120cm

四、动点问题的分类分类讨论问题

常见平面问题中动点问题的分类讨论；

例题4：正方形ABCD的边长为10cm，一动点P从点A出发，以2cm/秒的速度沿正方形的边逆时针匀速运动。如图，回到A点停止，求点P运动t秒时，P，D两点间的距离。

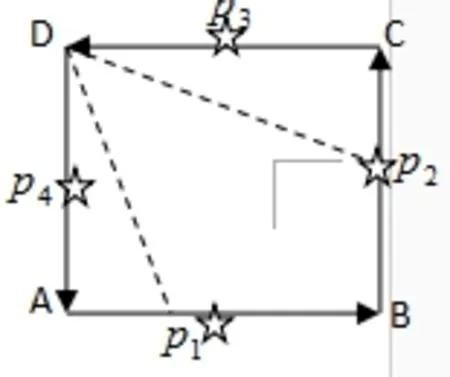
解：点P从A点出发，分别走到B，C，D，A所用时间是秒，秒，秒，秒，即5秒，10秒，15秒，20秒。

∴（1）当时，点P在线段AB上，(cm)

（2）当5≤t＜10时，点P在线段

（3）当10≤t＜15时，点P在线段CD上，|PD|=|P3D|=30-2t

（4）当15≤t≤20时，点P在线段DA上，|PD|=|P4D|=2t-30

综上得：

总结：本题从运动的观点，考查了动点P与定点D之间的距离，应根据P点的不同位置构造出不同的几何图形，将线段PD放在直角三角形中求解或直接观察图形求解。

分类讨论思想是在解决问题出现不确定性时的有效方法。线段及端点的不确定；角的一边不确定；三角形形状不确定；等腰三角形腰或顶角不确定；直角三角形斜边不确定；相似三角形对应角（边）不确定等，都需要我们正确地运用分类讨论的思想进行解决。分类讨论思想不仅可以使我们有效地解决一些问题，同时还可以培养我们的观察能力和全面思考问题的能力。

总之，初中数学中的分类讨论是一种重要的数学思维，有利于增强学生思维的条理性、缜密性和科学性。教师在教学中结合教材，创设情景，强化需要区分情况进行讨论的问题，启发学生积极思维，从而培养学生自觉应用分类讨论的意识。通过教师在教学中着重渗透数学思想方法的学习，相信会使学生在认知层次上得到极大的提高，收到事半功倍的效果。