面向复杂构造的油藏数值模拟网格剖分算法

2017-06-26孙鹏曹凯张慧贾志宾

计算机与数字工程 2017年6期

关键词：剖分交点油藏

孙鹏曹凯张慧贾志宾

（北京大学地球与空间科学学院北京100871）

面向复杂构造的油藏数值模拟网格剖分算法

孙鹏曹凯张慧贾志宾

（北京大学地球与空间科学学院北京100871）

随着油气勘探开发不断进行，目标油气田构造越来越复杂，然而当下商业建模软件对复杂构造的表达均不够理想，大多选择简化处理，误差较大。基于此，通过研究对Cookie-cutter和Stair-Step算法进行了改善，引入地质界面的无限切平面，通过切割求交等处理，实现了对大部分复杂构造的表达，包括逆断层、盲断层、多级Y断层、多级λ断层、尖灭等。网格模型单元格保持六面体形态，地质界面以“近阶梯”形式表达。一方面误差较小，构造描述精细；另一方面网格正交性较好，有利于油藏数值模拟计算。此外，算法对断层面、地层面、不整合面等地质界面采用无差别处理，逻辑简单，易于实现。为验证算法可行性，对局部复杂构造数据进行了剖分，网格质量较好。

网格；六面体；油藏数值模拟；复杂构造

Class NumberTP391

1 引言

网格剖分是油藏数值模拟的第一步，网格的质量对于数值模拟至关重要，直接影响模拟结果的可靠性［1～2］。随着油气资源勘探开发不断进行，目标油气田地质构造越来越复杂，对网格模型的复杂度、精确度要求越来越高。构建一种能保持地质三维特性、模拟精度高、生成速度快的网格，已成为油藏数值模拟最具挑战性的难题［3～5］。

目前大多数商业油藏模拟软件对结构化网格和非结构化网格都提供支持。但由于四面体网格具有单元形状不理想、刚度过高和体积锁死等缺点［6］，而PEBI、Radial等其他非结构化网格虽然克服了这些缺陷，但其构建、处理、可视化、附属性都非常困难，故非结构化网格没有得到广泛应用［7］。结构化网格仍是市场主流，其中角点网格使用最为广泛，尤以斯伦贝谢公司的“Pillar Grid”为代表，是油藏数值模拟和地质建模框架的行业标准［8］。

Pillar Gird基本满足了目前大部分需求［8］，但也有致命缺陷：1）对于倾斜断层，pillar会发生扭曲，使地质统计学算法产生误差，进而可能导致流体模拟错误；2）对于复杂构造（如出现盲断层、多级Y型断层、多级λ断层等），pillar方法无法剖分，只能进行大量简化，如垂直化断层、移除部分断层等［10～11］。因此，提出一个能完整表达任何复杂构造，并且适用于油藏数值模拟的网格，是十分有必要的。

针对上述问题，本文构建了一种基于复杂构造模型的油藏数值模拟网格，并在北京大学信息地质研究实验室开发的Creatar3.0三维可视化平台上进行了实现。该网格可较精确表达逆断层、盲断层、多级Y断层、多级λ断层、尖灭等绝大部分复杂构造，且方便油藏数值模拟计算，在实际应用中效果较好。

2 网格概述

为了克服Pillar Grid的缺陷，学者提出了几种新的网格形式，主要有Cookie-cutter和Stair-Step两种（如图1）［12］。这两种网格与pillar方法最大的不同在于，允许格子在k方向上切割断层，避免了大量扭曲格子的出现，从而保证了模型质量。Stair-Step网格以阶梯形式逼近地质界面，各网格为准立方体，有利于油藏数值模拟，但断层表达不够精确。Cookie-cutter网格在断层处采用cookie-cutter算法进行切割，可以精确表达断层，但切割时会发生退化或者产生多面体，无法保证正交性。Cookie-cutter网格模型进行油藏数值模拟时，一般需要先将断层面转化为Stair-Step形式。本文在上述网格基础上进行了改进，构建网格兼具二者优势。地层面、断层面、不整合面等地质界面采用“近阶梯”形式表达，既可以较精确表达复杂构造，又维持了六面体特性，正交性较好。

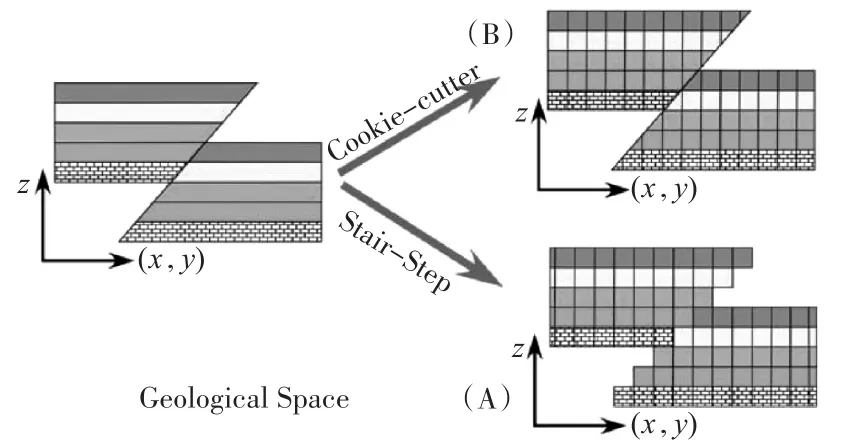
图1 “Stair-Step”（A）和“Cookie-cutter”（B）模式图［12］

2.1 网格横向组织

网格模型横向采用“XY regular”组织形式。如图2所示，水平面P为网格俯视投影，X方向线X(i)与Y方向线Y(j)正交，构成二维规则网格。网格交点称为原始点，记为点集V={v1，v2，…}；网格中心称为中心点，记为点集C={c1，c2，…}。网格X、Y方向步长保持一定，分别为dx，dy。dx，dy大小由网格分辨率决定，可根据实际需求进行调整。

图2 网格模型俯视图

2.2 网格纵向组织

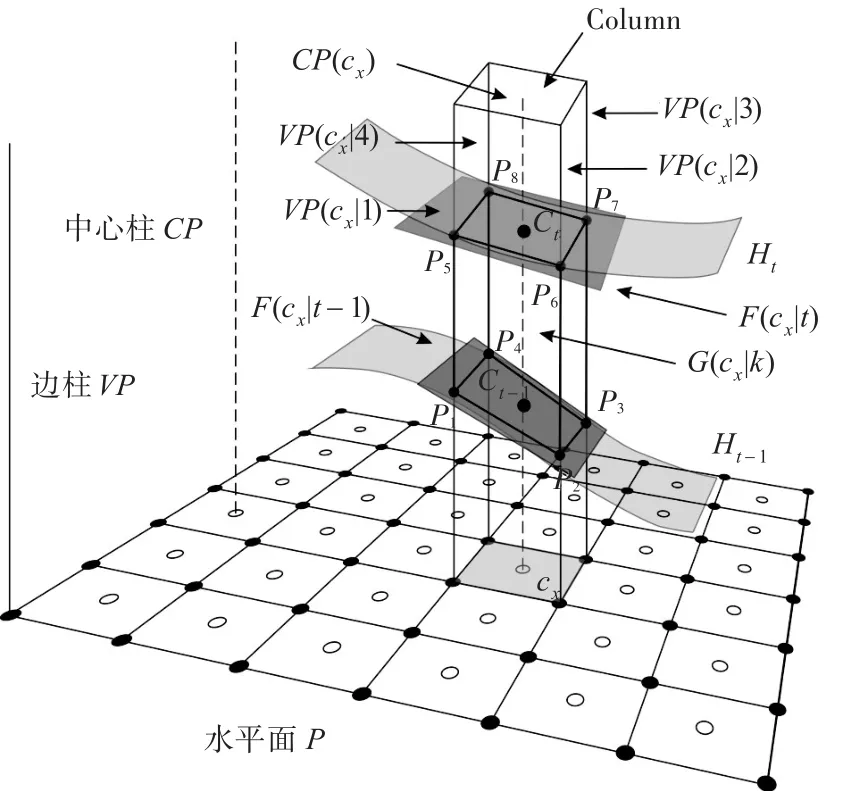
图3网格模型模式图

图3 所示符号定义如下，直线VP(vx)为通过原始点vx铅垂线，称为边柱。直线CP(cx)为通过中心点cx的铅垂线，称为中心柱。可以看出，每个中心柱CP(cx)周围环绕4个边柱，分别记为VP(cx|1)，VP(cx|2)，VP(cx|3)，VP(cx|4)。本网格划分方法对地层界面、不整合面、断层面等地质界面不做区分，采用相同处理方法，各界面统一表示为面集H={H1，H2，…}。曲面Ht-1、Ht为两个邻近地质界面，平面F(cx|t-1)、F(cx|t)为曲面Ht-1、Ht在点Ct-1、Ct处的切平面（无限连续面），Ct-1、Ct为中心柱CP(cx)与Ht-1、Ht的交点。

2.3 地质界面表达

按照前述方法构建的网格模型，单元格顶面或底面为地质界面相应位置的切平面，地层面、断层面、不整合面等地质界面则为多个格子的顶面或底面的集合，也就是说地质界面由一系列切平面以“近阶梯”状拼接而成。如图4所示，当分辨率足够大，切平面集合就能够精确近似地质界面。曲面Ht既可以是地层界面，也可以是断层面等其他地质界面，只是几何形态有所差异。单元格侧面为互相垂直的竖直平面，经过后期调整，可以充分保证网格正交性。网格模型各单元格均保持了六面体形态，避免了退化及多面体（多于6个面）的产生，降低了后期计算的复杂度。

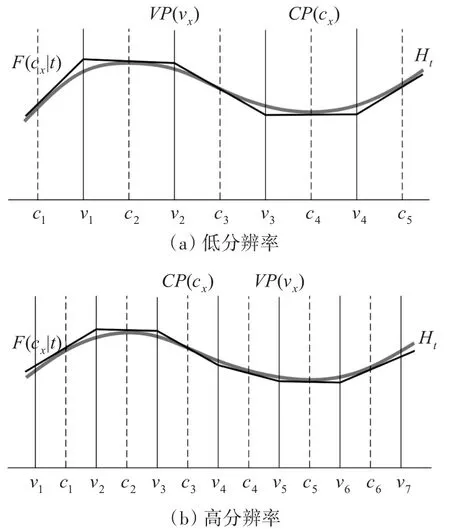
图4 不同分辨率下地质界面剖面图

3 构造表达

剖分算法对地层面、断层面、不整合面等地质界面不做区分，采用相同方法处理，构建任何复杂构造模型都可以理解为对地质界面的表达。而地质界面在几何上就是曲面，因此构建复杂构造模型就简化为对一系列曲面的表达。切平面拼接方式，可以处理绝大多数曲面组合，即可以表达大部分地质构造，包括逆断层、盲断层、多级Y断层、多级λ断层、尖灭等。

3.1 断层

断层是地质空间中最主要的构造，断层的表达是网格剖分算法的核心环节，其精细程度直接影响网格的质量，进而影响油藏数值模拟的准确度。本文构建网格模型对各种断层的表达如图5所示。

相比于传统剖分方法，对于正断层的表达，本文剖分算法优势不明显。但对于逆断层、盲断层，尤其是复杂构造的表达，本方法则具有显著改进：通过切平面求交的方法，有效解决了逆断层地层重复、盲断层不断透地层等问题；地层、断层的无差异处理，简化了复杂构造的表达。从而使得逆断层、盲断层的表达与正断层无异，复杂构造变为简单构造的简单叠加。

3.2 尖灭

尖灭是指地层在横向空间展布上变薄以至消失的现象，与地层堆积时的地理环境、地壳运动情况有关。油气盆地先后经历沉积及后期构造运动，尖灭广泛存在。准确表达尖灭有助于判断储层位置，对于油气开发具有重要意义。尖灭具体表达如图6所示，构建方法与上述断层一致。尖灭处六面体没有发生退化，而是以一个“薄面”（如图6加粗线段所示）进行模拟。既保持了六面体特性，又较精确地表达了尖灭。

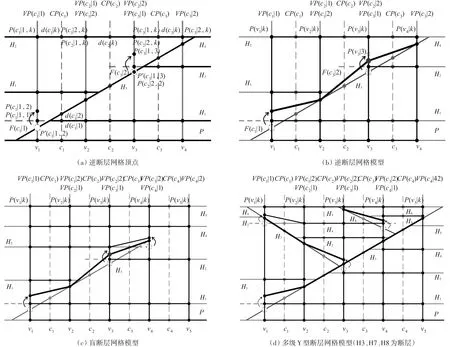
图5 断层网格模型剖面

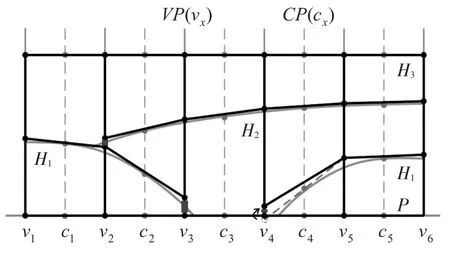
图6 尖灭网格模型

4 网格剖分

剖分算法以地质界面一致性处理和切平面拼接为核心思想。实现过程以线面求交为主要技术手段。具体剖分流程如图7所示，包括构造模型准备，初始参数设置，中心柱求交，求取无限切平面，边柱求交，同一化处理及网格连接七个步骤。

4.1 构造模型

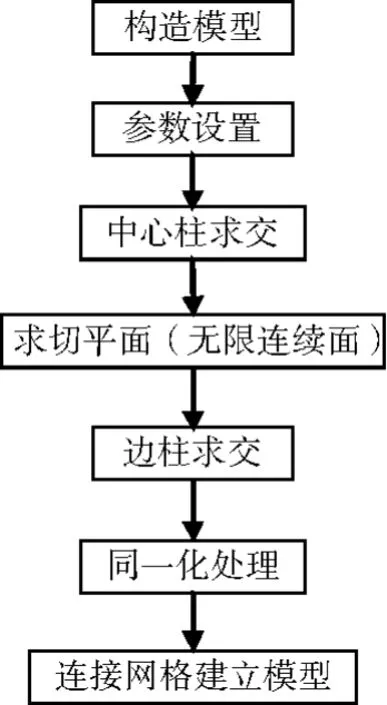
图7 网格剖分流程

构造模型是本文剖分方法的基础，构造模型复杂度及精确度决定了网格模型的质量。本文选用Creatar3.0可视化平台进行构造建模，该软件可处理任意复杂构造［12］，为本方法的实现提供了保障。如图8所示，地层面、断层面采用不规则三角网进行表达，以下步骤对地质界面进行处理即为对不规则三角网进行处理。

图8 构造模型

4.2 参数设置

在进行网格剖分之前，需要对坐标系、分辨率等关键参数进行初始化。坐标系Z轴方向定为竖直向上，X轴、Y轴方向需要根据实际情况设定。选择原则为尽量减少无效网格，尽可能体现油藏构造特性。实际应用中，可依据地质构造走向、地质体形态进行设定，如选取构造主应力方向或地质体俯视图最小外包矩形的两边方向作为X轴、Y轴方向。网格分辨率通过步长dx、dy进行描述，dx、dy取值需综合考虑原始数据分布情况和实际需求，如一般以井间有两三个以上网格单元为佳。

4.3 中心柱求交

根据X轴、Y轴方向，dx、dy数值，可求出原始点及中心点坐标，进而完成水平方向二维规则网格构建。三维空间中边柱、中心柱z坐标为0，x、y坐标分别与原始点、中心点坐标相同。获得中心柱坐标后，可依次求出每个中心柱与各地质界面的交点。将计算结果存放在Column类型对象中，以便后续计算。求交过程中，可先行判断边柱与地质界面外包矩形空间关系，倘若二者相交，再详细计算边柱与不规则三角网的交点坐标，否则就是没有交点，不必再具体求交，这样可减少大量计算。

Column类用于记录网格剖分过程中的重要信息，其主要属性如表1所示。Column类几何含义同图3中Column，每个Column有一个中心柱及四个边柱，边柱坐标存放在Fiber中，中心柱坐标不需要直接记录，可通过切点x、y坐标表达。每个Column中的切点按空间位置从下到上的顺序进行记录，此外还要记录属性信息，即与其相交的地质界面的属性。Column按I、J进行索引，其中I方向平行于X轴方向，J方向平行于Y轴方向。

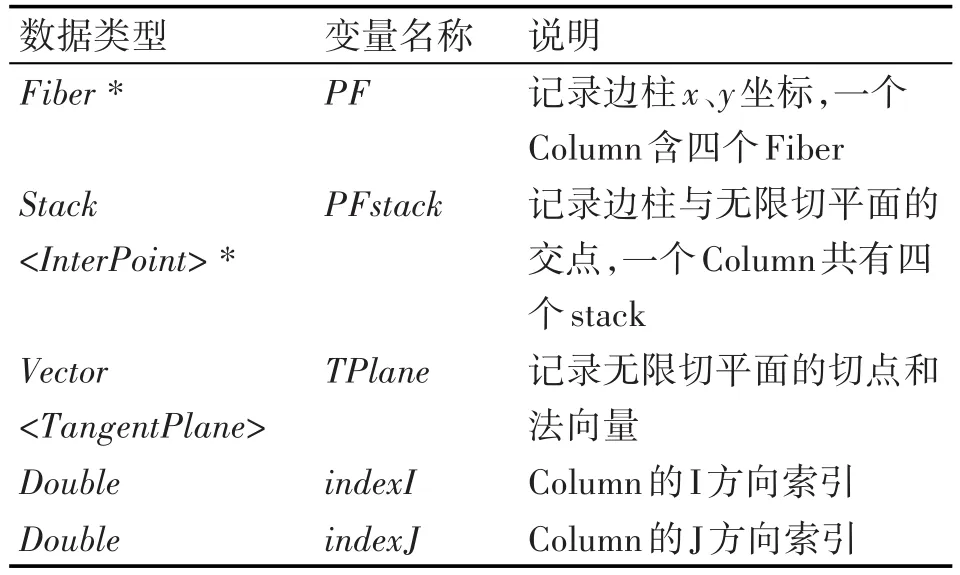
表1 Column类主要属性

4.4 求切平面

切平面记录在TPlane数组中，通过切点和法向量进行表达，其中切点已由上步求出，接下来求出切平面法向量即可。根据切点与不规则三角网的空间关系，分为三种情况（如图9所示）：1）切点位于三角形内部；2）切点位于三角形边上；3）切点位于三角形顶点。情况1），三角形所在平面的法向量即为切平面的法向量，情况2）、3），可取关联三角形法向量的平均值，作为切平面的法向量。本文采用面积加权平均法求取平均值，即

图9 切平面法向量计算

4.5 边柱求交

根据I、J索引遍历Column，对于其中每一个边柱，按照从下到上顺序与切平面求交，并将交点坐标及其属性存放在对应的InterPoint栈中。求交过程中，需要对每一个交点进行如下判断：与前一交点纵坐标进行比较，如若该交点空间位置在前一交点之上，则继续求下一交点；如若不然，则会发生交叉，需将该交点向上平移小段距离ds至前一交点之上。ds取值要综合考虑地质体形态及模型分辨率。

相比于直接与地质界面求交，引入切平面具有两方面优势。一方面由于切平面无限大，每个单元格都可求出8个交点，确保了网格的六面体形态；另一方面，切平面具有单一属性（由切点属性决定），消除了同一单元格边柱交点属性不一致而引发的歧义。

4.6 同一化处理

对于每一个边柱，由于为4个Column共享，交点坐标一共求出4套。然而地质含义及网格连接要求网格具有同一性，即同一边柱同一属性点只能有一个，故需要对4套交点进行同一化处理，本文采用均值法。具体而言，依次遍历每一个边柱，对每一个边柱做如下处理：1）找出该边柱关联的4个Column，并取出相应的InterPoint栈；2）比较4个栈顶元素，选取属性相同且空间位置相近的交点，求出其平均值；3）弹出计算过的栈顶元素，并用平均值对其交点坐标进行更新；4）重复1）～3），直至4个栈都为空。对于模型边缘不足4套交点的，按实际数量处理。

4.7 连接网格

同一化处理后，Column中存放的交点就是网格模型单元格的顶点。按照Column中交点的组织方式依次进行连接，即可获得单元格，进而完成网格模型构建。连接网格过程中，可同时对单元格I、J、K索引及地层属性进行赋值。

5 模型举例

为了验证剖分算法正确可行，本文选择局部复杂构造数据，在Creatar3.0可视化平台上进行了剖分试验。该区域由多级Y字形断层限定，包括盲断层、尖灭等构造现象。剖分结果如图10所示，质量较好。

图10 应用效果图

6 结语

本文在Cookie-cutter和Stair-Step算法基础上进行了改善，在一定程度上解决了复杂构造建模问题。

该方法通过切平面切割的方式，以近阶梯形式表达地质界面，实现了对绝大多数复杂构造的精确表达，包括逆断层、盲断层、多级Y断层、多级λ断层、尖灭等。所建模型正交性较好，有利于进行油藏数值模拟。此外，算法对断层、地层、不整合面采用一致性处理，逻辑简单，易于实现。

但模型对倾角近垂直的地质界面表达不够理想，变形较大。该模型不能直接用于油藏数值模拟，还需要进行细分、粗化等后期处理。网格质量的优劣尚需通过更多的实际应用，进行检验。

［1］Hocker C，Thom J.3-D Grid Types in Geomodeling and Simulation--How the Choice of the Model Container Determines Modeling Results［C］//2009 Annual Convention&Exhibition of the American Association of Petroleum Geologists，Denver，Colorado，2009.

［2］Bennis C，Sassi W，Faure J.One More Step in Gocad Stratigraphic Gris Generation：Taking into Account Faults and Pinchouts［C］//SPE European 3-D Reservoir Modeling Conference，Stavanger，Norway，1996.

［3］Aziz K.Reservoir Simulation Grids：Opportunities and Problems［J］.Journal of Petroleum Technology，1993，45（7）：658-663.

［4］Mallison B，Sword C，Viard T，et al.Unstructured Cut-Cell Grids for Modeling Complex Reservoirs［J］.Spe Journal，2013，19（2）：340-352.

［5］Lasseter T J，Jackson S A.Improving integrated interpretation accuracy and efficiency using a single consistent reservoir model from seismic to simulation［J］.The Leading Edge，2004，23（11）：1118-1121.

［6］徐能雄，武雄，汪小刚，等.基于三维地质建模的复杂构造岩体六面体网格剖分方法［J］.岩土工程学报，2006（8）：957-961.

XU Nengxiong，WU Xiong，WANG Xiaogang，et al.Approach to automatic hexahedron mesh generation for rock-mass with complex structure based on 3D geological modeling［J］.Chinese Journal of Geotechnical Engineering，2006（8）：957-961.

［7］Gringarten E J，Haouesse M A，Arpat G B，et al.Advantages of Using Vertical Stair Step Faults in Reservoir Grids for Flow Simulation［C］//2009 SPE Reservoir Simulation Symposium，Woodlands，Texas，USA，2009.

［8］King M J，Ballin P R，Bennis C，et al.Reservoir modeling：From RESCUE to RESQML［J］.Spe Reservoir Evaluation &Engineering，2012，15（2）：127-138.

［9］Filho Z M，Brazil E V，Sousa M C，et al.Cutaway Applied to Corner Point Models［C］//SIBGRAPI，Ouro Preto，Brazil，2012.

［10］Wu X H，Parashkevov R.Effect of Grid Deviation on Flow Solutions［J］.Spe Journal，2009，14（1）：67-77.

［11］Gringarten E J，Arpat G B，Haouesse M A，et al.New Grids for Robust Reservoir Modeling［C］//2008 SPE Annual Technical Conference and Exhibition，Denver，Colorado，USA，2008.

［12］Jayr S，Gringarten E，Tertois A L，et al.The need for a correct geological modelling support：The advent of the UVT-transform［J］.First Break，2008，26（10）：73-79.

［13］Mao P，Zhhaoliang L，Zhongbo C，et al.3-D Geological Modeling-Concept，Methods and Key Techniques［J］. Acta Geologica Sinica-English Edition，2012，86（4）：1031-1036.

［14］Wu Q，Xu H.An approach to computer modeling and visualization of geological faults in 3D［J］.Computers& Geosciences，2003，29（4）：503-509.

［15］Cherpeau N，Caumon G，Lévy B.Stochastic simulations of fault networks in 3D structural modeling［J］.Comptes Rendus Geoscience，2010，342（9）：687-694.

Partitioning Algorithm of Reservoir Numerical Simulation Grid for the Complex Structure

SUN PengCAO KaiZHANG HuiJIA Zhibin
（School of Earth and Space Sciences，Peking University，Beijing100871）

As the continuous exploration and development of oil and gas resources，the geological structure of target oil and gas field become more and more complicated.However，the commercial modeling softwares are not ideal，most of which simplify the complex structure and then model it，having a large error.Based on the Cookie-cutter and Stair-Step algorithm，a new hexahedron grid was proposed.This approach introduced the infinite tangent plane，and expressed the geological interface with“near Stair-Step”.On one hand，almost all the complex structure can be modeled，including reverse fault，blind fault，multi-Y faults，multi-λ faults，pinch-out and so on.On the other hand，cells preserve hexahedron and have a good orthogonality，which is favorable to calculate.Further more，the geological interfaces of fault，layer and unconformity are treated with the same method，lowing the algorithm complexity and easy to implement.The algorithm was verified with the local data of complex structure.The results are in line with expectation and meet the requirement.

grid，hexahedron，numerical simulation of reservoir，complex structure

TP391

10.3969/j.issn.1672-9722.2017.06.004

2016年12月2日，

2017年1月10日

国家自然科学基金项目“基于语义的多分辨率储层数据组织与管理”（编号：41472113）资助。

孙鹏，男，博士研究生，研究方向：网格剖分算法。曹凯，男，博士研究生，研究方向：三维地质构造建模和相建模。张慧，女，硕士研究生，研究方向：三维地质建模。贾志宾，男，硕士研究生，研究方向：三维地质建模。