常见的证明三角形重心的方法

云南省德宏州盈江县第一高级中学 尤廷田

一、引言

三角形是几何中的基本图形，三角形的重心是关于三角形的重要定理，于是证明三角形重心的存在性能够给学习者提供一个展示自身才华的机会，提高知识的应用能力，还能加深学习者对重心的理解程度，更好地认识三角形，同时也从一个侧面反映数学知识的严谨性。

二、三角形重心的证明

三角形的重心：三角形三条中线相交于一点，这点叫做三角形的重心

证明：

法一：如图一设AD、BECF分别是∆ABC的边BC、CAAB的中线，则

由塞瓦定理得AD、BECF、三线平行或相交于一点。而AD、BE相交于G点，故AD、BECF三线相交于G点。

命题得证[2]。

法二: 如图二设AD、BECF分别是∆ABC的边BC、CAAB的中线。设AD与BE相交于G，AD与CF相交于H，

设

则

故

于是得

即

同理

从而知∆ABC的三条中线相交于一点。命题得证。

法三：如图三设AD、BECF分别是的边B、CCAAB的中线，设A、DBE相交于G.建立仿射坐标系则A(0,0),B(1,0),C(0,1)D(0.5,0.5),E(0,0.5),C(0.5,0.)设G分有向线段AD成定比x,

故

设,G分有向线段BE成定比y,故由点的唯一性得

即G点在CF上，从而知∆ABC的三条中线相交于一点。命题得证。

法四：设AD、BECF分别是∆ABC的边B、CCAAB的中线，以BC所在的直线为x轴，BC边上的高AO所在直线为y轴，OC的长度为1个单位长度建立直角坐标系（如图四），则C(1,0).设A(0,a),B(b,0),则D(0.5+0.5b，0),

E(0.5,0.5a),F( 0.5b, 0.5a),AD、BECF

所在直线方程分别为：

方程组

故AD、BECF相交于一点。命题得证。

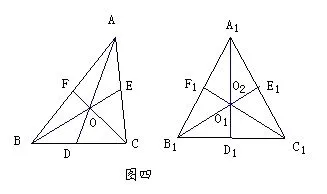
法五：∆ABC是任意一个三角形，∆A1B1C1是一个正三角形，A1D1,B1E1,C1F1,是∆A1B1C1的三条中线（如图五），设A1D1,B1E1,相交于O1，C1F1,A1D1相交于O2.由正三角形的三线合一的性质可得

故O1与O2重合，即正三角形的三条中线交于一点。

由平面仿射几何基本定理，存在唯一的仿射变换T将∆A1B1C1变为∆ABC.由于仿射变换保同素性和接合性，得D1、E1、F1的象D、E、F分别在BC、CA和AB上。O1的象O就是AD、BE、CF三线的交点。由仿射变换保简比，可得D、E、F分别是BC、CA和AB的中点，即AD、BE、CF是∆ABC的中线。命题得证。

法六：∆ABC是任意一个三角形，∆A1B1C1是一个正三角形，A1D1、B1D1分别是 ∆A1B1C1的边B1C1、A1C1的中线，设A1D1、B1E1相交于O1，过O1作O1F1⊥A1B1垂足为F1，连结C1F1（如图六）.由正三角形的三线合一的性质可得

故以O1为圆心O1D1为半径可作一圆内切于∆A1B1C1（如图七），切点分别为D1、E1、F1.由布利安双定理可得A1D1、B1E1、C1F1相交于一点O1.又，是B1D1=B1F1,D1是B1C1的中点，且B1C1=A1B1，故F1是A1B1的中点。

由平面仿射几何基本定理，存在

唯一的仿射变换T将∆A1B1C1变为∆ABC.由于仿射变换保同素性和接合性，得D1、E1、F1的象D、E、F分别在BC、CA和AB上，O1的象就是AD、BE、CF三线的交点O.由仿射变换保简比，可得D、E、F分别是BC、CA和AB的中点，即AD、BE、CF是∆ABC的中线。命题得证。

法七:∆ABC是任意一个三角形，AD、BE、CF分别是BC、CA、AB边的中线。连结DE、DF、EF（如图八）.

由三角形的中位线定理可得DE∥AB，DF∥AC,EF∥BC即DE与AB，DF与CA，EF与BC分别相交于无穷远点G、H、I.无穷远点G、H、I在无穷远直线上。由代沙格定理的逆定理可得AD、BE、CF相交于一点。又AD、BE相交于普通点O，故CF过点O。命题得证。

综上所述：第一，向量方法很简捷、方便，因为它最大的优势是运算，在共面向量中取两个不共线的向量，以它们作为基，通过很流畅的运算把其余向量都用它们表示出来，然后对所得的向量进行比较，根据唯一性，令对应系数相等即可把有关系数确定出来，使问题得到解决或有所进展。此外，如果把向量运算和数值（坐标）运算结合起来就能更多地使用代数方法，因而具有一般性的优点。它作为解决数学问题的强有力的工具，优势是不言而喻的。

第二，在仿射几何中可以相互转化的图形叫做仿射等价图形。在仿射等价图形中，所有的图形具有相同的仿射性质。因此，只要我们知道了哪些图形是仿射等价图形后，我们就可以在这些图形中找出最简单或比较简单的图形，只要将它们的不变性及不变量弄清楚了，也自然把这些仿射等价图形的性质弄清楚了。例如，所有的三角形是仿射等价图形，其中最简单的三角形是正三角形，所以，为了证明任意三角形具有某种仿射性质，我们只须证明正三角形具有这种性质就可以了。