中学数学课时教学目标设计存在的问题及对策

刘权华

摘要：当下课时教学目标设计存在目标缺失、目标偏离课程标准、表述不具体、三维目标割裂等问题。对教学目标设计重要性的忽视、教学观念与教育行为不一致、课程目标与课时目标关系模糊、课程标准分解技术薄弱是这些问题形成的主要原因。教师必须认真领会课时教学目标设计在教学中的作用，基于课程标准和学情，学会从课程目标到单元教学目标，再到课时教学目标的分解。

关键词：中学数学；课时教学目标；设计；问题；对策

中图分类号：G632 文献标志码：A 文章编号：1673-9094（2017）06A-0069-04

不管课程标准会作怎样的修改，教学目标都会有多样的呈现方式，在当下就教学目标的可操作性而言，“三维目标”（知识与技能，过程与方法，情感、态度与价值观）仍是比较合适的方式。但在调研中我们发现许多教师的教案存在如下问题：课时教学目标缺失、三维目标割裂、行为主体错位、行为表现抽象等，其中最大的问题是对课程目标到课时教学目标的分解技术薄弱。

为什么出现这种状况？教师往往认为，“目标是重要，我已经看过了，心中有数”；“主要考虑的是教学过程的设计，至于目标，只是个‘摆设而已”；“‘过程与方法、‘情感、态度、价值观的目标不会写，难以描述，也懒得去写”。当下的一些课时教学目标已变成“说起来重要做起来不要”的内容，课时教学目标设计日益残缺化或被形式化。笔者对某区105位中学数学教师开展问卷调查，收回有效问卷100份，其中“你会基于课程标准进行目标分解，并认真设计课时教学目标吗？”的答案统计显示，会的，占20.0%，多数会的，占26.0%，偶尔会的，占36.0%，几乎不会的占18.0%。这一调查结果反映出很多教师课时教学目标设计意识不强，不会分解和描述教学目标，认识不到设计教学目标的重要性。

一、课时目标设计存在的问题及表现

（一）目标缺失

目标缺失主要表现在：教案没有设置课时教学目标，“教学目标”一栏空白或敷衍了事，残缺不全。大多数情况就是教师简单地写几句关于“知识与技能”的目标，而很少提及“过程与方法”、“情感、态度与价值观”的目标。

（二）课时教学目标偏离课程标准

课时教学目标偏离课程标准首先表现在课程理念“涛声依旧”。虽然课程标准修订版即将下发，但是课程倡导的“‘用教材教，教师应根据学生的实际情况，对知识进行‘重组，实现‘人人学有价值的数学，人人都能获得必需的数学，不同的人在数学上得到不同的发展”的主旨是不会变的。但不少教师仍然把教科书视为唯一的课程资源，课程实施中的“课程”几乎等于教科书，无论面对什么时期的学生，什么层次的班级，教什么和怎么教几乎完全取决于教科书。学生在基于教科书的课程实施中，成为了一个被不断灌输的容器。长此以往，学生的数学核心素养很难得到发展。[1]

课时教学目标偏离课程标准其次表现在行为主体错位。课堂学习的行为主体是学生，不是教师，教学目标描述的应是学生学的行为，而不是教师教的行为。但是形如“使学生掌握……”，“培养学生……能力”之类的表述，指向教师的行为主体错位，仍然大面积出现在教师的教案中。

（三）课时目标表述不具体

课时目标应是具体的、微观的。因此，数学课时目标强调可操作性、具体化，是经过课堂教学，能看得见的“学生的变化”。课时目标表述不具体体现在教师把课时教学目标写成“进一步体会数形结合思想”，而没有具体目标的陈述，也没有明确规定学生应参加的活动，更没有从哪个层面反映出学生体会到了数形结合思想。由于教师们根本没有着眼于“活动”“过程”和“体验”，因而显得抽象和不可考量。

（四）三维目标人为割裂

有些教师在设计教学目标时，因为不会描述，直接忽略过程与方法和情感、态度与价值观目标。三维目标应是融为一体的，知识技能的掌握必须通过过程与方法，情感、态度与价值观的目标也只有在过程与方法中才能形成和实现。所以，严格意义上来讲，把三维目标人为割裂，分别表述，确实有待商榷。

二、问题成因分析及对策

导致以上课时教学目标设计问题的原因分析如下。

（一）对课时目标设计的重要性认识不够

很多老教师对于课程标准虽然認同，却不去实践。他们习惯对着课本和教参，凭借自己的经验备课。因为他们一直使用的方法照样出成绩，所以并不愿意大幅度地改革课堂。另外长期教学毕业班的教师，自认为目标了然于胸，或认为课时目标只是设计中的一个“标签”，故对这种文本分解不屑一顾。

正是由于没有真正意识到课时教学目标对于课堂教学的意义和价值，才导致了没有明确目标的“空”对“空”教学；正是因为目标缺失，才呈现出在风雨中飘摇，“魂不附体”的课堂；正是这种飘忽不定的课堂，注定了当下教学“高负轻质”现象的大量存在。

（二）教学观念与教学行为存在“落差”

大部分教师对课程改革的理念都很认可，但落实在教学中却有不同程度的“落差”。有统计数据显示：绝大多数教师对一些数学教学观念完全赞同。其中认可度最高的教学观念是“教学内容的设计应以学生的认知水平为基础”，高达97.7%，认可度最低的是“课堂教学要给学生留出足够的自主学习时间”和“课堂教学要面向全体学生，要照顾到有困难的学生”，赞同率也有85%。但是，教学行为的实现程度却远远低于这个数字。其中最高的，“能根据学生的认知发展规律循序渐进进行教学”才50.7%，认为完全能够做到的教师比例只有31.5%。由此可见，教师认同的教学理念与教学行为之间存在着显著差异。原因主要是：1.老教师教育思想跟不上，虽然认同，但无法实现；2.改革需要付出更多的时间和精力，这些因素阻碍了教师自认为的“冒险”；3.知识老化、师生之间存在代沟，教师没有真正把握学情。

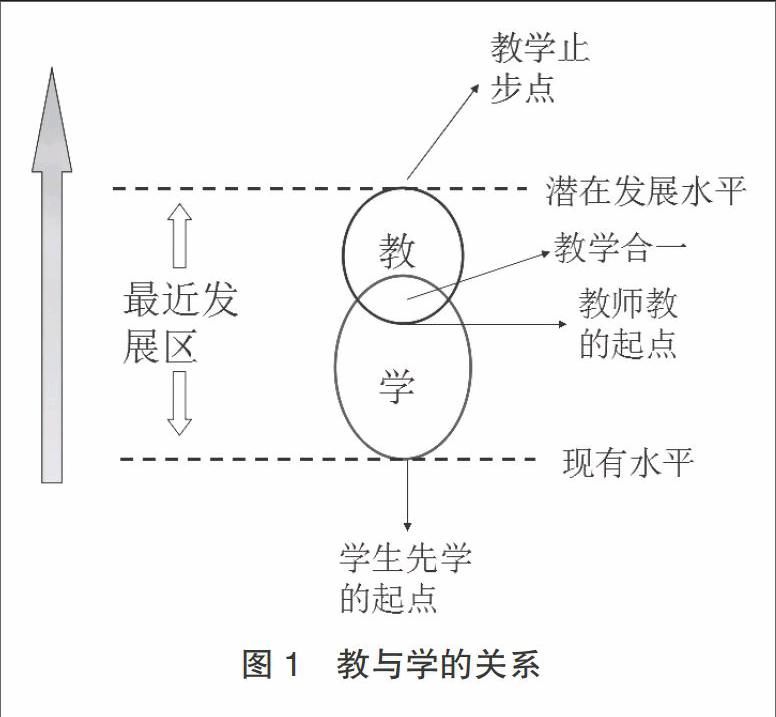
为了纠正这个“落差”，教师在设计课时目标时，应牢记两个“有没有”：有没有认真阅读课程标准，并在课标指导下研究过一份完整的高考试卷？设计的教学活动有没有设定在大多数学生“最近发展区”的教学合一地带？教的起点应在哪儿？许多教师会不假思索地回答：“当然是学的起点！”其实并不是这样。如图1所示，教师教的起点和学生学的起点还有好长一段距离，并且学生的“最近发展区”并不是处于同一水平、绝对的静止状态，不同学生有不同的“最近发展区”。对于同一个学生，在学习不同的内容时，或者在不同的教学环境中，不同教师指导下都会有所不同。我们切忌以静止的眼光和简单化、一刀切的心态看待学生，而要用发展的观点、变化的眼光看待每一个学生。

如何根据学生的现有基础、潜在可能，在知识、能力、方法、情感等方面找到教学合一的最佳着力点，这确实是一个技术活。这就要求我们教师在研究课程标准和教材的同时，还要把握动态的、真实的学情，努力做到以生为本，以学定教。

（三）课时目标缺乏主体性、层次性和可观测性

在“平行与垂直”一课的教学中，有的教师设计的教学目标中有这样一条：培养空间想象能力和联系实际的意识和能力。如何培养学生的空间想象能力呢？途径、策略是什么？为何越过空间知觉、空间表象直接上升到空间想象能力？显然太空太大。有的教师在本节课的教学中，简单地写上两条：1.使学生理解垂直和平行的概念；2.使学生体会垂直和平行在生活中的广泛应用。很明显，主体错位，表述太过粗略，层次不强，与知识紧密相关的技能目标和过程性目标根本就没有，且目标不可测量。

课时教学目标的设计需要包含以下几个要素：主体明确、具体、可测、有层次、可实现。其实，设计课时教学目标很简单，抓住ABCDE即可：Audience（行为主体），Behavior（行为动词），Condition（行为条件），Degree（表现程度），Evaluation （评价、评估）。还是以“平行和垂直”为例，可以设定为如下几条：1.学生（主体）通过操作、想象、观察（行为动词）等活动（行为条件），理解平行和垂直的概念（表现程度），能正确判断平行与垂直（评价评估）；2.学生经历两直线动态变化的探索过程，感受平行和垂直的各自特征和内在联系，发展空间观念；3.学生通过寻找身边的平行和垂直现象，体验数学与生活的联系。虽然有时省略主体，但是心中一定要有。

（四）对“三维”目标理解模糊或对整体目标不会分解

三维目标不是独立的三个目标，更不是先去完成一个目标，再去完成下一个目标，而应融合在一起。它们是学会、会学与乐学的关系，知识与技能目标立足于让学生学会，过程与方法目标立足于让学生会学，而情感、态度与价值观目标立足于让学生乐学。尽管知识、技能目标是基础性的目标，处于核心地位，是每节课必须要达到的目标，必须予以充分的重视，但这不应该成为教师们不屑或不愿写后两个目标的“理由”。

三维目标书写的方式，并没有也不必要有一个统一模式。在调研中，我们发现有的是分三条明确标明“知识与技能”、“过程与方法”、“情感、态度与价值观”目标，有的是去掉三个具体名称，但具体内容还是相对应的三条，有的是将两维或三维目标融合在一起，这都未尝不可。笔者更倾向于最后一种模式，即融合在一起去设计，因为“知识与技能”是“过程与方法”、“情感、态度与价值观”的载体，三者是相伴而行的，并在一个教学活动中实现的。当然，有时根据需要，不一定每一节课都要牵强附会地加以表述，表述时也不一定非要面面俱到，更不一定要平均用力。但是必须要力求做到行为词语明确、具体，用可观察和可测量的词语来陈述。[2]

（五）对课程目标、单元教学目标和课时目标的关系认识模糊

课程目标是最高层次的学习目标，它规定的是一门课程的整体教学要求，比较抽象，达成目标时间较长，具有宏观性和长远性。单元教学目标是一个单元所有学习内容的总体目标。而课时目标则是教师在一节课中要达成的教学目标，具有微观性、短期性。三者不能混为一谈。

例如，人教版（必修5）第一章“解三角形”的第二节应用的举例（第一课时）的课时教学目标设计为1.通过对事例的解决，能够运用正弦定理和余弦定理解三角形的有關问题，解决两种类型的距离测量问题：一个不可到达的点到一个可到达的点之间的距离；两个不可到达的点之间的距离。2.经历将距离测量问题转化为解三角形问题的过程。认识实际应用问题的研究方法：分析—建模—求解—检验，能够类比解决问题。3.体验将具体的实际问题转化为抽象数学问题的过程与方法，培养分析问题、解决问题的能力，通过探索解决问题方法的多样性，发展学生的创新意识，培养学生的交流、合作能力，并体会数学的应用价值。三维目标明确、具体、可操作。如果去掉以上三条课时教学目标中的后半部分内容，显然就不是具体、明确和可操作的了。而恰恰相反，许多教师就是将没有具体可操作内容的单元教学目标作为课时教学目标。同理，课程目标和单元教学目标、单元教学目标和课时教学目标也不同，此处不再赘述。

三个层面的目标不一样，那么如何将课程标准落实到单元目标，再具体到课时目标呢？

笔者以苏教版高中数学必修2“直线与平面垂直的判定”为例予以说明。这节课的内容标准是：以长方体为载体，直观认识和理解空间点、线、面的位置关系；能用数学语言表述有关平行、垂直的性质与判定，并对某些结论进行论证。整体目标分解到单元目标再到课时目标，必须要以学生的现时的认知水平为起点，不仅要思考“教什么”和“怎么教”，还要考量“为什么教”和“教到什么程度”。由于学生已学习了必修2的第一单元，故可设计如下的单元目标：以线、面的有关定义，四个公理和定理为出发点，通过直观感知、操作确认、思辨论证，认识和理解空间中线面平行、垂直的有关性质与判定，通过直观感知、操作确认，归纳出有关判定定理和性质定理。考虑到学生已学过集合的知识，教师可将点、线、面的位置关系分别用文字语言、图形语言和符号语言进行描述和比较。再通过国旗与地面、火车与地面的关系等生活场景，使学生感知数学来源于生活，使生活问题数学化。又因为学生已经学习了直线与平面的位置关系、直线与平面平行的判定与性质，并已初步学会了转化思想，因而教师可再将单元目标具体化为如下课时目标：1.学生能借助具体实例，抽象概括出直线与平面垂直的含义，并能准确理解其定义；2.通过折纸实验，门窗旋转等具体操作，归纳出直线与平面垂直的判定定理，并能分别用文字语言、符号语言和图形语言表述线面垂直的判定定理，在此基础上运用定理解决空间位置关系的简单证明；3.进一步培养空间观念、体会线线垂直与线面垂直相互转化的思想；4.亲身经历数学研究的过程，体验探索的乐趣，增强学习立体几何的兴趣。[3]

没有科学的、适切的课时教学目标设计，就不可能有高效的教学效果；没有基于课程标准的教学目标，就很容易出现许多人为的教学问题。课时教学目标设计不是可有可无的，更不是一项点缀、一种摆设，它是教师进行教学的重要环节。制定全面、具体、适宜的课时教学目标，是提高教学质量的关键。广大教师应本着对教育负责的态度，认真领会课程标准在教学设计中的灵魂作用，学会课程目标到课时教学目标的分解，同时以学生寻求真知为目标，综合分析教材，结合学生实际和自身教学经验，以超越教材的方式，与时俱进地制定出以人为本、既符合课程标准又具可操作性的课时教学目标。

参考文献：

[1]崔允漷，李锋.基于课程标准教学的理论诉求[J].基础教育课程，2014（11）.

[2]梁靖云，吕素巧.教学目标设计初探[J].教育理论与实践，2014（8）.

[3]付强，等.数学课堂教学目标的制定与实施[J].中学数学教学参考，2014（3）.

责任编辑：石萍