改进气体流量计算方法的迫榴炮内弹道模型

赵雨馨,白 真,赵 彤,杨 力,黄 萌,梁益铭

(1 中国兵器工业第203研究所,西安 710065;2 清华大学机械工程系,北京 100084)

改进气体流量计算方法的迫榴炮内弹道模型

赵雨馨1,2,白 真1,赵 彤2,杨 力1,黄 萌1,梁益铭1

(1 中国兵器工业第203研究所,西安 710065;2 清华大学机械工程系,北京 100084)

内弹道计算对炮弹发射有重要意义。文中研究了迫榴炮发射迫弹时的内弹道模型,将膛内气体流出过程类比喷管气体流动过程,针对气体流出量的计算进行了详细的讨论。然后在Matlab软件中运用四阶Runge-Kutta法对某型120 mm自行迫榴炮发射迫击炮弹内弹道过程进行插值求解,并用CFD++软件对发射过程进行仿真。利用该模型计算所得膛压及出炮口速度与实验所测基本一致,火药气体流动状态与仿真结果相符,仿真与实验结果均证明了该模型的正确性、可靠性。

内弹道;迫榴炮;气体流量

0 引言

迫榴炮是从传统的迫击炮和榴弹炮基础上演变而来,同时具有迫击炮及榴弹炮的优势,极大的提高了火炮的战斗性能。其炮管刻有膛线,既可采用线膛方式发射榴弹也可采用滑膛方式发射迫击炮弹[1]。因此,迫榴炮发射迫弹时无法进行闭气,会有大量的火药气体从弹炮间隙流出,造成额外的能量损失,所以迫榴炮内弹道虽与迫击炮内弹道问题有相通之处却更为复杂。在迫击炮经典内弹道方程中对火药气体的流出量没有详细的讨论,采用了系数修正方法[2]。Acharya R学者较为深入的探讨了迫击炮发射迫击炮弹的数值分析方法和仿真计算方法[3-4],建立了不同发射药的燃烧模型并进行有限元仿真,得到不同时刻膛内气体的压力分布,但没有对气体泄出量进行分析。国内现有的存在气体从弹炮间隙流出的有代表性的内弹道计算方法中,孙明亮等对弹丸结构和射角进行了修正,得到了评估迫弹散布密集度内弹道模型[5];景凤理分析了迫榴炮内弹道过程,并对迫榴炮发射迫击炮弹进行了一维两相流数值模拟[6]。归纳现有文献可知,现有的内弹道研究方法通常忽略了气体流出量的问题,而系数修正方法的缺陷在于需要通过经验与实验试凑,较难进一步提高内弹道模型精度。

文中研究针对迫榴炮发射迫弹时大量火药气体流出的问题,利用类比拉瓦尔喷管流体流动的方法,建立流量方程,除此之外,对气体状态方程和能量方程也重新进行了讨论,弥补了用修正系数估算的缺陷,并进行了仿真和实验对比。

1 内弹道方程组的建立

1.1 基本假设

迫击炮弹装药分为两部分,一部分称为基本装药,它是装填在用厚纸做成的、带有底火的基本药管内,插在炮弹的尾管内,起着传火的作用;另一部分称为辅助装药,它是由环形药或其他形状火药分装成等重量的药包,固定在弹尾传火管的周围(如图1所示)。

发射时,基本装药底部被击针碰撞从而点火,当达到破孔压力后,火药气体从传火孔流出,并点燃包围在传火管周围的辅助装药。

图1 迫击炮弹装药结构

根据内弹道过程及装药特点提出以下假设:

1)基本装药和辅助装药同时燃烧时按各自的燃烧规律燃烧。药粒均在平均压力下燃烧,燃烧均遵循几何燃烧定律及燃烧速度定律。

2)热损失不作直接计算,通过减小火药力的方法,间接修正热损失的影响。

3)用系数φ来考虑其他的次要功。

4)单位质量火药生成火药气体的燃烧温度及所放出的能量均为定值,燃气在内弹道过程中成分不变,因此虽火药气体温度因膨胀而下降,但火药力f、余容α及比热比k等均视为常数。

5)仅考虑弹丸沿迫榴炮身管方向一维运动。

进而设定在发射过程中的某一瞬间t,已燃百分数为ψ,气体相对流出量为η。这时膛内的气体压力为p,温度为T,弹丸行程为l,弹丸速度为v。根据这些变量建立起内弹道方程组。

1.2 燃烧方程

火药的指数燃速方程为:

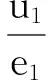
(1)

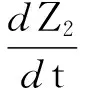
(2)

式中:Zi代表火药已燃相对厚度;ui代表火药燃速;ei代表二分之一火药起始厚度;ni表示火药燃速系数(式中脚标i=1代表该参数为基本装药参数,i=2代表该参数为辅助装药参数)。

符合几何燃烧定律的气体生成速率方程为:

(3)

式中:α1、α2分别代表基本装药和辅助装药占火药总量的比重;χi、λi、μi为火药的形状参数。

将火药气体从弹炮间隙流出的过程类比拉瓦尔喷管内流体的流动[7-8],如图2所示。

图2 类比拉瓦尔喷管流体流动示意

将火药气体在某一瞬间的流动视为一维准定常等熵流动,则满足如下伯努利方程[9]:

(4)

求出弹前、后气体相对弹丸压强,Ω为外力场势能,C为常数。然后利用压强比例关系及扩张比判定火药气体的流动状态(亚音速流动、扩张段产生激波、喷管出口产生斜激波或者欠膨胀状态),求出气体流动Ma。q(λ)与Ma符合如下关系:

(5)

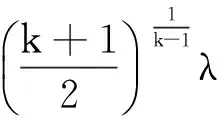
(7)

式中:p0为总压;T0为总温;R为气体常数;s′为喷管喉部横截面积,即炮膛横截面积与弹丸定心部横截面积之差。则可得气体相对流出量的微分方程:

第五，自然计算是非终止的。也就是说，自然计算系统与其环境持续相互作用，并且只有当系统(例如，生物体、群体)停止存在时，该相互作用才终止。

(8)

式中：ω为装药总质量,也为生成的火药气体总质量。

由于有气体流出,在某瞬间t,留在膛内的气体量为ω(ψ-η),其中ω为火药总质量,则状态方程为:

S1p(l+lψ)=RTω(ψ-η)=fτω(ψ-η)

(9)

式中：lψ=l0[1-Δ/(ρp(1-ψ))-αΔ(ψ-η)],ρp为火药密度,l0为药室长,Δ为装填密度;S1为炮膛横截面积。

1.4 弹丸运动方程

利用速度位移关系及牛顿第二定律可得:

=v

(10)

(11)

式中:m为弹丸质量;s为弹丸最大横截面积,即定心部横截面积。

1.5 能量平衡方程

某一时间间隔dt内,火药燃烧量ωdψ,燃烧温度为T1,定容比热为Cv,定压比热为Cp,则所放出的能量为CvT1ωdψ,这里所消耗掉的能量主要有两部分:一部分为推动弹丸做的功φmvdv;另一部分为气体流出所带走的能量CpTωdη。留在膛内的能量为d[CvTωd(ψ-η)],则根据能量守恒定律,有:

d[CvTω(ψ-η)]=CvT1ωdψ-φmvdv-CpTωdη

(12)

令τ=T/T1,式中Cv、Cp取整个过程平均值,可得能量方程如下:

(13)

2 基于Matlab的内弹道方程组解算

综上所述可得方程(1)、(2)、(3)、(8)、(10)、(11)、(13)七个微分方程和方程(9)一个代数方程,其中共有Z1、Z2、p、ψ、η、τ、v、l、t九个未知数,将t视为自变量,将基本装药破孔瞬间的各个变量值作为内弹道方程组的初始条件,利用四阶Runge-Kutta法对某型120 mm自行迫榴炮发射迫击炮弹内弹道过程进行插值求解[10-11]。

计算得到:火药全部燃尽需要4.361 ms,出炮口时间为13.77 ms,出炮口时速度为414.2 m/s,最大膛压于点火后3.03 ms达到,为122.7 MPa,弹炮间隙气体流出量达20.2%,比一般迫击炮大得多,火药气体流动状态判断如表1所示。膛压时间曲线如图3所示,速度时间曲线如图4所示,火药气体相对流出量关于时间的曲线如图5所示。

图3 膛压-时间曲线

时间/s火药气体流动状态0～9×10-5产生正激波9×10-5～1.377×10-2产生斜激波

图4 速度-时间曲线

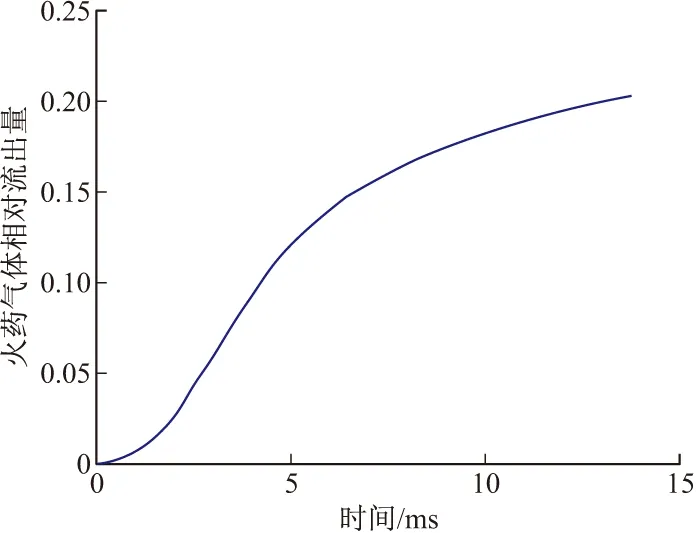
图5 火药气体相对流出量-时间曲线

3 基于CFD++的仿真分析

运用CFD++流体仿真软件对发射过程进行流固耦合仿真,得到发射过程3个典型时刻以马赫数为参考的流出气体状态,见图6。

图6(a)显示点火后5×10-5s,火药气体从弹炮间隙流出产生正激波的状态,即类比的喷管喉道中产生正激波状态;图6(b)显示点火后6×10-4s在弹头处产生斜激波的状态,即类比的喷管出口产生斜激波状态;图6(c)显示点火后10-2s在弹头处产生斜激波的状态,即类比的喷管出口产生斜激波状态,观察到此时斜激波形态与6×10-4s时斜激波形态略有不同,因为此时弹丸速度相对6×10-4s时的速度大得多,弹头部位边界层厚度变大,斜激波的角度也有所不同。仿真结果与计算判断流体流动状态相符,验证了此模型中类比喷管方法的正确性。

图6 运用CFD++软件所得仿真结果

4 实验验证

利用电子测压器测得膛压关于时间的曲线[12],将其与计算曲线进行对比(如图7所示)。

图7 膛压实测值与计算值对比

最大膛压的误差为0.5%,达到最大膛压时间的误差为1.3%,膛压变化趋势吻合良好。通过以上对比,可证明文中计算内弹道理论模型正确、可靠。

5 结论

文中提出了一种计算迫榴炮内弹道气体流出量的新方法,将炮膛内气体流动过程类比喷管内气体流动,并在经典迫击炮内弹道模型基础上进行改进和完善。运用文中方法对某型120 mm自行迫榴炮发射迫击炮弹进行内弹道解算,计算值与实验、仿真均吻合良好,验证了该迫榴炮内弹道模型的准确性与可靠性。该模型可为以后的炮弹发射及膛内流场分析提供理论基础。

[1] 卜杰. 双用途火炮——迫榴炮 [J]. 现代军事, 2005(1): 52-54.

[2] 张小兵. 枪炮内弹道学 [M]. 北京: 北京理工大出版社, 2014: 281-289.

[3] ACHARYA R, KUO K K. Finite element simulation of interior ballistic processes in 120-mm mortar system [C]∥23rd International Symposium on Ballistics. TARRAGONA:[s.n.], 2007.

[4] ACHARYA R. Modeling and numerical simulation of interior ballistic processes in a 120 mm mortar system[D]. Philadelphia: University of Pennsylvania, 2009.

[5] 孙明亮, 周晓东, 雷彬. 一种改进的迫击炮内弹道仿真模型 [J]. 价值工程, 2013(9): 283-284.

[6] 景凤理. 迫榴炮内弹道过程分析及数值模拟 [D]. 南京: 南京理工大学, 2007.

[7] 杜桂贤, 金文栋, 邵万仁, 等. 轴对称矢量喷管有效喉道调节方法 [J]. 航空动力学报, 2015, 30(8): 1818-1825.

[8] 王平, 刘学山, 乔立民. 轴对称拉瓦尔喷管流场分析 [J]. 飞机设计, 2013(2): 23-26.

[9] 张兆顺, 崔桂香. 流体力学 [M]. 北京: 清华大学出版社, 2006: 260-271.

[10] 孙艳馥, 鲍雪. 高膛压火炮内弹道仿真研究 [J]. 装备制造技术, 2013(11): 167-168.

[11] 柯彪, 高跃飞, 罗炳华, 等. C#与MATLAB混合编程在内弹道设计中的应用 [J]. 弹箭与制导学报, 2013, 33(5): 129-132.

[12] 裴东兴, 沈大伟, 张瑜, 等. 弹底压力测试技术研究 [J]. 弹箭与制导学报, 2012, 32(5): 196-198.

[13] 张锦斌. 火炮测速雷达的应用与发展 [J]. 无线电工程, 1994(1): 9-19.

The Interior Ballistic Model of the Mortar-howitzer with Improved Gas Flow Calculation Method

ZHAO Yuxin1,2,BAI Zhen1,ZHAO Tong2,YANG Li1,HUANG Meng1,LIANG Yiming1

(1 No.203 Research Institute of China Ordnance Industries, Xi’an 710065, China; 2 Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China)

Interior ballistics calculation had significant value to the projectile launching. In this paper, the interior ballistic model of the howitzer projectile was studied, and the process of the gas flow in the nozzle was compared with that of the process of the gas flow in the chamber. The calculation of gas outflow was discussed in detail. Then, the Matlab software was used to solve the interpolation of interior ballistic process of a 120 mm self-propelled howitzer fired mortar projectile by using the fourth-order Runge-Kutta method, and the launching process was simulated by CFD++ software. The chamber pressure and the muzzle velocity calcalated by using the model were consistent with the experimental measurement results, and the propellant gas flow state and the simulation results were consistent. Thus, the model in this study was proved to be accurate and reliable.

interior ballistics; mortar-howitzer; gas flow rate

2016-08-31

赵雨馨(1993-),女,黑龙江哈尔滨人,助理工程师,硕士研究生,研究方向:发射内弹道与弹丸结构。

TJ012.1

A