空间与地面菲涅尔区的特性研究

邹高翔,童创明,王 童,孙华龙

(空军工程大学防空反导学院,西安 710051)

空间与地面菲涅尔区的特性研究

邹高翔,童创明,王 童,孙华龙

(空军工程大学防空反导学院,西安 710051)

雷达导引头在下视探测超低空目标时,集中在第一菲涅尔区的多径能量会影响雷达的探测能力。针对菲涅尔区的特性,定义了电磁波传输的空间菲涅尔区和超低空探测下的地面菲涅尔区。根据惠更斯-菲涅尔定理,建立了空间和地面菲涅尔区的数学模型。通过仿真分析了馈源与接收天线距离和工作波长对第一空间菲涅尔区的影响,得到了第一地面菲涅尔区随弹目投影间距离和投射余角的变化规律。研究结果为处理多径信号、对反射面进行有限截断提供了理论依据。

超低空探测;空间菲涅尔区;地面菲涅尔区

0 引言

目前,超低空突防武器以其灵活机动、雷达散射截面小的特点,使其被雷达所探测的概率大大降低,成为我国空防安全所面临的一大难题[1]。雷达导引头下视探测低空目标时,接收到的除了目标回波外,还包括多径信号[2-3]和背景杂波[4]。背景杂波包括海浪、山脉和气象等所带来的复杂回波信号。多径信号是由雷达的直射波、地面反射波和目标回波组合产生的[5],多径信号在空间中可以发生多次耦合,使得最终接收到的信号在幅度和相位上会发生较大变化,在仰角上会导致波束分裂[6-7],对雷达导引头探测和跟踪目标会带来较大的影响。

根据惠更斯-菲涅尔定理,在电磁波的传输过程中,由于波阵面上二次波源所辐射的电磁波相互干涉、叠加,波阵面上的每一点到接收点的距离各不相同,接收点所接收到的信号场强也会发生相应的变化。在电磁波的传输过程中,电磁信号传输的能量主要集中在第一菲涅尔区[8]。在对抗超低空突防的过程中,需要解决的主要问题之一是如何减小第一菲涅尔区中的多径信号[9]。

目前,在微波和信号传输的很多领域,都有关于菲涅尔区的研究。文献[10]针对基于GPS信号的海面目标的被动探测问题,研究了第一菲涅尔区随卫星高度角的变化规律;文献[11]研究了倾斜地面对地面反射的最小菲涅尔椭圆区的影响;文献[12]研究了在随机海洋粗糙面上的有效散射区域的计算方法;文献[13]研究了地基雷达的地面菲涅尔区的数学模型。总的来说,针对菲涅尔区的研究,缺乏统一的定义方式和分类方式,针对菲涅尔区特性的研究也比较少。文中针对空间菲涅尔区和地面菲涅尔区两个方面,给出其完整的定义,并根据惠更斯-菲涅尔定理,建立了第一空间菲涅尔区和第一地面菲涅尔区的数学模型,分别对其随不同因素的变化特性进行了分析和研究。

1 空间与地面菲涅尔区

1.1 空间菲涅尔区

空间菲涅尔区是指在视距空间内,雷达馈源和接收天线间的电磁波信号进行传输时,所占用的空间区域。这个区域在物理形状上呈现的是一个椭球体,如图1所示。

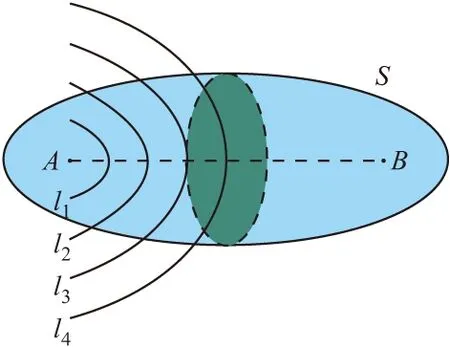
图1 空间菲涅尔区示意图

图1中点A为雷达馈源,点B为接收天线,l1、l2、l3和l4为不同时刻的波阵面,根据惠更斯-菲涅尔定理,每一个波阵面上的点都是进行第二次辐射的球面波波源,其具体特征表现在同一时刻到达接收天线时,波程差的不同。在实际的应用中,只关注其能量主要集中的区域,即第一空间菲涅尔区,即图中椭球面S所指区域。

1.2 地面菲涅尔区

雷达导引头在下视探测目标时,会发射雷达信号来探测目标,目标在接收到雷达波的照射后,会散射回波信号,雷达接收到回波信号后进行信号处理从而得到目标的方位、俯仰角和速度信息。然而在实际情况中,由于超低空突防目标的飞行高度通常在较低位置,目标所散射的回波会通过地面的反射再返回至雷达。通过地球表面反射到达雷达的信号称为多径信号。多径信号由镜面反射分量和漫反射分量构成,当反射面起伏程度较小时,以镜面反射为主;当反射面起伏程度较大时,以漫反射为主。

如图2所示,G平面为水平面,C点为雷达导引头,D点为突防目标,C′点为雷达导引头在水平面上的投影,D′点为突防目标在水平面上的投影,E点为突防目标相对于水平面的镜像,HC为雷达导引头的高度,HD为突防目标的飞行高度,椭球面S是以C点为源点、E点为接收点的第一空间菲涅尔区。

雷达下视探测目标时,由于地面的反射作用,在相对于水平面会形成一个“镜像”目标,源点与“镜像”目标所构成的空间菲涅尔区与地面相交所形成的椭圆面,称为地面菲涅尔区。同空间菲涅尔区相同,在实际的应用中,只关注其能量主要集中的区域,即第一地面菲涅尔区,即图中椭圆面F所指区域。通常,反射面也就是图2中G平面所表示的水平面往往是远大于第一菲涅尔区F,但多径反射的能量绝大多数来自于反射面的第一地面菲涅尔区,反射面的特性主要取决于第一地面菲涅尔区。

图2 地面菲涅尔区示意图

2 菲涅尔区计算模型建立

2.1 空间菲涅尔区计算模型

空间菲涅尔区的分区是根据该区域边界上的二次波源,进行二次辐射到达接收天线的波程差来定义的,如图3所示。

图3 空间菲涅尔区分区示意图

图3为空间垂直截面图,圆面P为某一时刻电磁波的波阵面,椭圆面S1、S2和S3分别表示第一、二、三空间菲涅尔区的边界,点P1、P2、P3分别为波阵面P与椭圆面S1、S2、S3的交点,即属于第一、二、三空间菲涅尔区的二次波源。将波程用d表示,dAB表示雷达馈源A与接收天线B的距离,即电磁波的直接传输波程;在波阵面P上易知关系dAP1=dAP2=dAP3,根据二次波源所在位置,其波程有如下关系:

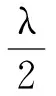
(1)

(2)

(3)

经过点P1的总波程与直接传输波程相差一个半波长λ/2;经过点P2的总波程与直接传输波程相差两个半波长λ/2;经过点P3的总波程与直接传输波程相差3个半波长λ/2。由此归纳出空间菲涅尔区的分区条件:空间菲涅尔区的第n个区的边界定义为有比直接传输波程长nλ/2的传输路径,即:

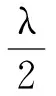
(4)

式中n取正实数。

由上述推导可知,相邻两个菲涅尔区存在着λ/2的波程差,体现在相位上为反相关系,在空间的传输中能量会彼此削弱。设第n个区域所传输的能量为Pn,则有关系:P1>P2>…>Pn,根据相邻菲涅尔区的反相关系,可以认为最终接收天线B所接收到的能量为P≈P1/2,因此,在空间中电磁波能量的传输主要集中在第一空间菲涅尔区。

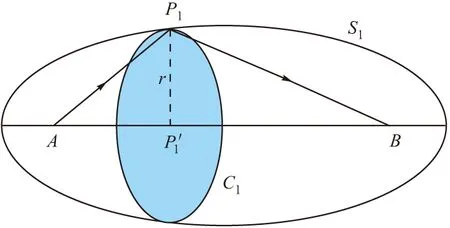
图4 第一菲涅尔区示意图

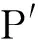
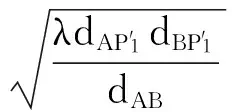
(5)

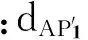
为了得到第一菲涅尔区的空间数学模型,建立空间直角坐标系如图5所示。

图5 空间直角坐标系下的第一空间菲涅尔区

在平面xoz中,第一空间菲涅尔区所在的椭球面与平面xoz相切的平面为椭圆面,其中有关系:

(6)

由上式可得:

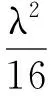
(7)

联立式(6)、式(7),得到椭圆面方程:

(8)

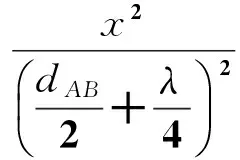
(9)

2.2 地面菲涅尔区计算模型

雷达导引头工作时,通常是下视探测目标,而此时,地面菲涅尔区就是由源点与“镜像”目标所构成的空间菲涅尔区与地面相交所形成的椭圆面。同空间菲涅尔区相同,在实际的应用中,只关注其能量主要集中的区域,即第一地面菲涅尔区。在文献[16]中,构建了陆基雷达反射区域的计算模型,文中运用该文献中的建模方法,对雷达导引头下视工作时地面菲涅尔区的模型进行构建,建立空间坐标系如图6所示。

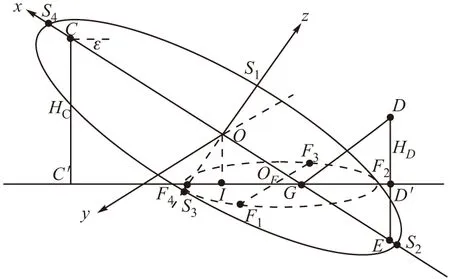
图6 空间直角坐标系下的第一地面菲涅尔区

在图6中,雷达导引头投射余角为ε,点G为镜面反射点,椭球面S是以C点为源点、E点为接收点的第一空间菲涅尔区,点S1、S2、S3和S4分别为椭球面S与xoz平面的交点,椭圆F1F2F3F4是椭球面与水平面的交面,其中点F2和点F4位于线段C′D′上,其中线段F1F3⊥F2F4,线段IO是线段C′D′的中垂线。设椭圆F1F2F3F4的长轴、短轴和焦距分别为a、b和c,由下列几何关系:

(10)

将长、短轴a、b代入求出椭圆F1F2F3F4的表达式:

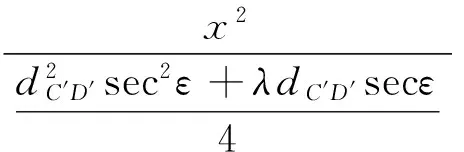
(11)

式(11)即为过直线F2F4且垂直于IO的平面方程表达式。

由下列距离关系

(12)

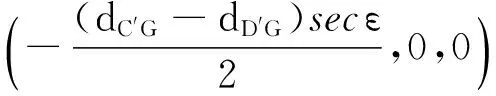
(13)

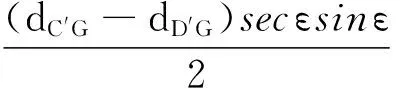
(14)

(15)

将式(11)所表示的平面与椭球S1S2S3S4相交,得到椭圆F1F2F3F4,由图6中几何关系,运用右手法则得到直线F1F3的方向向量

(16)

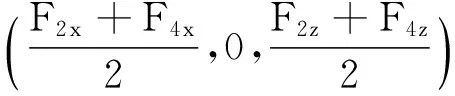
(17)

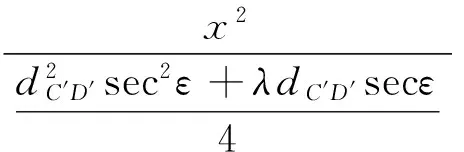
(18)

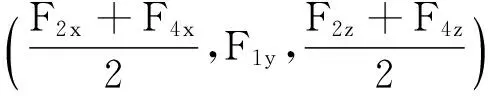
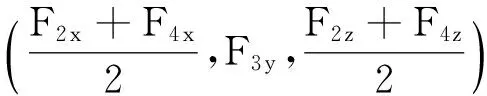
(19)

设椭圆F1F2F3F4面积为SF1F2F3F4,得到

(20)

如图6中的几何关系,由于:dC′G-dD′G=dC′D′-2HDcotε

(21)

工作波长λ≪dC′D′,在实际情况中,擦地角ε很小,化简式(11)、式(13),联立式(20),得到

(22)

这就是第一地面菲涅尔区的数学模型。

3 菲涅尔区的特性研究

3.1 空间菲涅尔区的特性研究

由式(9)表示的第一空间菲涅尔区所在的椭球面可知,第一空间菲涅尔区的大小主要取决于雷达馈源A与接收天线B的距离dAB和雷达的工作波长λ,为了研究影响第一空间菲涅尔区的因素,下面分别对雷达馈源A与接收天线B的距离dAB和雷达的工作波长λ对第一空间菲涅尔区的影响进行分析。

为了便于直观的分析,在进行分析前进行条件假设:由于第一空间菲涅尔区的半径相对于雷达馈源与接收天线的距离是很小的,所以将其雷达馈源与接收天线的距离设置在百米范围内,以便于从仿真图中观察其特性。

3.1.1 雷达馈源与接收天线距离的影响

在研究雷达馈源A与接收天线B的距离dAB对第一空间菲涅尔区的影响时,设置雷达馈源工作在S波段,雷达的工作频率保持不变,其工作频率为f=3 GHz,对应工作波长为λ=0.1 m,对比3个不同距离dAB1=100 m、dAB2=200 m、dAB3=300 m下第一空间菲涅尔区的仿真图如图7所示。

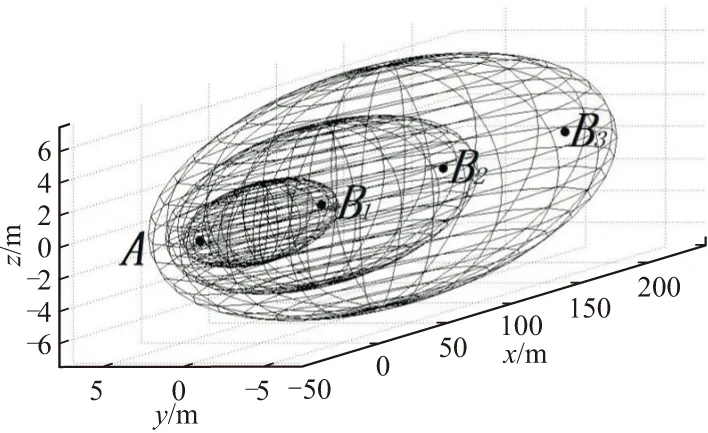
图7 第一空间菲涅尔区随雷达馈源与接收天线距离变化的图像

由图7可以直观地看到,在雷达的工作波长保持不变时,第一空间菲涅尔区的大小,随着雷达馈源A与接收天线B的距离dAB增大而增大,其区域的主要形状基本不发生变化。

3.1.2 雷达馈源与接收天线距离的影响

在研究雷达的工作波长λ对第一空间菲涅尔区的影响时,设置雷达馈源A与接收天线B的距离dAB=100 m,取雷达馈源工作在S、C、X波段,频率分别为f1=3 GHz、f2=6 GHz、f3=10 GHz,对应工作波长为λ1=0.1 m、λ2=0.05 m、λ3=0.03 m,对比3个不同工作波长下第一空间菲涅尔区的仿真图如图8所示。

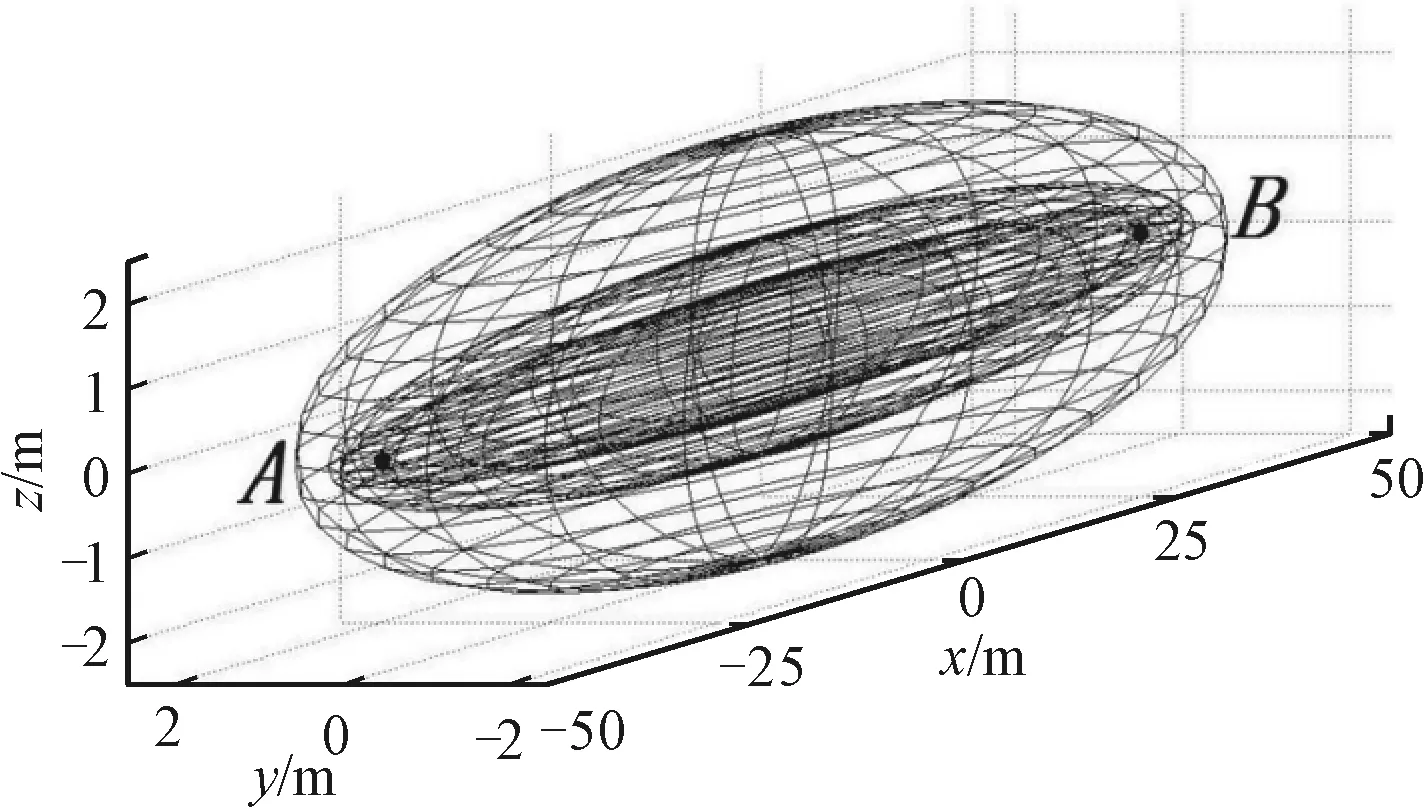
图8 第一空间菲涅尔区随雷达工作波长变化的图像

从外到内分别为λ1、λ2和λ3所对应的第一菲涅尔区。由图8可以直观地看到,在雷达馈源与接收天线的距离保持不变时,第一空间菲涅尔区的大小与形状,均随着工作波长的变化而变化。具体表现为,随着工作波长的逐渐减小,第一空间菲涅尔区所在的椭球面逐渐收缩,而长轴端几乎不发生变化,表明了电磁波在传输时,能量随着工作频率的增加,也就是工作波长的减小,其能量的传输更加集中于第一空间菲涅尔区。在进一步的仿真中,在极高频的情况下,第一空间菲涅尔区收缩近似为一条线段,能量的传播集中在一条线段中,符合电磁波的光本质。

3.2 地面菲涅尔区的特性研究

第一地面菲涅尔区的面积与突防目标的高度HD、雷达导引头的投射余角ε、雷达的工作波长λ和雷达导引头在水平面上的投影点C′与突防目标在水平面上的投影点D′的距离dC′D′有关,下面根据式(21)所建立的模型,研究不同因素对地面反射区域面积的影响。

在进行探讨前设置下列假设:

1)突防目标为巡航导弹,因此设置突防目标的高度HD为一常量;

2)突防目标的高度HD单位在米数量级,雷达导引头在水平面上的投影点C′与突防目标在上平面上的投影点D′的距离dC′D′在千米数量级;

3)工作波长λ≪dC′D′,且雷达导引头的投射余角ε很小。

3.2.1 导引头投影与目标投影距离的影响

设置突防目标的高度HD为20 m,雷达导引头工作在S波段的6个点频上(2 GHz、2.4 GHz、2.8 GHz、3.2 GHz、3.6 GHz、4 GHz),导引头的投射余角ε为10°,导引头投影与目标投影距离dC′D′由100 m变化到3 000 m,其第一地面菲涅尔区的面积(m2)的模拟结果如图9所示。

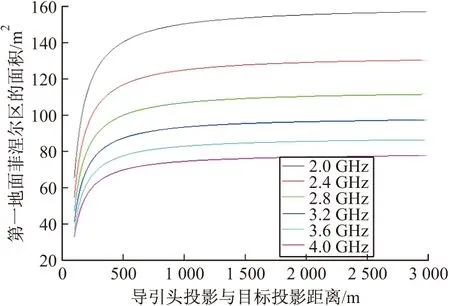
图9 第一地面菲涅尔区的面积随导引头投影与目标投影距离变化的图像

通过观察图像,可以得到以下结论:

1)在导引头投影与目标投影距离较近时,第一地面菲涅尔区的面积随着导引头投影与目标投影距离的增加而迅速增大,导引头投影与目标投影距离达到某一值时,面积的增长趋势逐渐趋于平缓,最后到达某一值后几乎不变;

2)在S波段,随着频率的增加,第一地面菲涅尔区的面积所达到的稳定值变小,而趋势变化的转折点不随频率的变化而变化。

通过仿真分析,由于近程范围内所呈现的剧烈变化特性,在研究多径条件下雷达第一地面菲涅尔区的面积时,主要以研究近程为主。在近空防御超低空目标时,第一地面菲涅尔区面积变化趋势的剧烈,对导引头的探测能力的影响较大,与实际情况相符。

3.2.2 电磁波投射余角的影响

设置突防目标的高度HD为100 m,导引头投影与目标投影距离dC′D′为1 000 m,雷达导引头工作在S波段的6个点频上(2 GHz、2.4 GHz、2.8 GHz、3.2 GHz、3.6 GHz、4 GHz),导引头的投射余角ε由0.01 rad变化到0.25 rad,其第一地面菲涅尔区的面积(m2)模拟结果如图10所示。

图10 第一地面菲涅尔区的面积随导引头的投射余角变化的图像

通过观察图像,可以得到以下结论:

1)第一地面菲涅尔区的面积在导引头的投射余角ε较低时,随着导引头的投射余角的增加迅速增大,当达到某一角度时,面积达到最大值;在此之后,随着导引头的投射余角的增加迅速减小,在大约0.08 rad时减小趋势逐渐趋于平缓;

2)在S波段,随着工作频率的增加,第一地面菲涅尔区的面积的最大值逐渐减小,而所对应导引头的投射余角基本没有变化,因此,可以认为,面积最大值所对应的导引头的投射余角与频率无关,而最大值随频率的增大而减小。

由上可得,当导引头的投射余角为某角度时,其第一地面菲涅尔区的面积会达到一个最大值,而这个最大值在数值上是非常大的,由前文可知,这个面积的最大值就是,在突防目标的高度确定的情况下,水平面与第一空间菲涅尔区所在的椭球体相切得到的最大面积,与定义是相符合的。

4 结束语

针对低空突防目标的探测,面临的最大问题就是来自地海面的多径信号,在对目标与环境散射特性进行分析时,通常要对目标和环境进行建模,然而建立的环境模型如果过大,则对其散射特性计算的时间复杂度会大大增加,影响信号处理的速度。文中通过建立第一空间菲涅尔区和第一地面菲涅尔区的数学模型,并在数学模型的基础之上对影响该区域范围变化的多个因素进行分析,得到第一空间菲涅尔区和第一地面菲涅尔区的变化特性。研究结果为处理多径信号、对反射面进行有限截断提供了理论依据。真实环境中,空间和地面的物理属性和电磁属性往往是非常复杂的,对多重气象条件下的第一空间菲涅尔区,和粗糙、时变、多层介质条件下的第一地面菲涅尔区研究是下一步的工作。

[1] NASIC Public Affairs Office.Ballistic & cruise missile threat:NASIC-1031-0985-13 [R]. 2013.

[2] 王利军, 郭建明, 郝晶. 多径效应对雷达探测低空巡航导弹的影响 [J]. 雷达科学与技术, 2010, 8(1): 7-14.

[3] LUO Wei, ZHANG Min, ZHOU Ping, et al. Analysis of multiple scattering from two-dimensional dielectric sea surface with iterative kirchhoff approximation [J]. Chinese Physics B, 2010, 19(8): 379-383.

[4] 陈博涛, 谢拥军, 李晓峰. 真实地形环境下低空雷达目标回波信号分析 [J]. 西安交通大学学报, 2010, 44(4): 103-107.

[5] JOHNSON J T. A numerical study of scattering from an object above a rough surface [J]. IEEE Transactions on Antennas & Propagation, 2002, 50(10): 1361-1367.

[6] 崔嵩, 李岩, 郑昌. 海面多路径效应对舰载雷达探测低空目标的影响 [J]. 舰船电子工程, 2009, 175(1): 104-106.

[7] 王晓冰, 童广德, 梁子长. 海面多路径下比相测角误差仿真分析 [J]. 制导与引信, 2009, 30(2): 11-15.

[8] 徐振海, 肖顺平, 熊子源. 阵列雷达低角跟踪技术 [M]. 北京: 科学出版社, 2014: 31-33.

[9] 黄大卫. 无人机遥控遥测中多径效应分析 [J]. 南京航空航天大学学报, 2009, 41(增刊): 43-46.

[10] 马建国, 曹可劲, 张磊, 等. 基于GPS信号的海面目标被动探测 [J]. 系统工程与电子技术, 2011, 33(5): 987-991.

[11] 罗光胜, 张志刚, 孙剑平. 倾斜地面对短波天线通信的影响 [J]. 舰船电子工程, 2012, 222(12): 63-67.

[12] 李彦佐，金亚秋. 随机粗糙海面的多路径海杂波频谱数值模拟 [J]. 微波学报, 2005, 21(4): 6-11.

[13] 黄树军, 孙合敏, 闫世强. 一种求解陆基雷达地面反射区域面积的模型 [J]. 空军雷达学院学报, 2002, 16(1): 31-33.

Studies on the Characteristics of the Space Fresnel Zone and the Ground Fresnel Zone

ZOU Gaoxiang,TONG Chuangming,WANG Tong,SUN Hualong

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

When radar seeker detected ultra-low altitude targets in downward-looking, the energy of multipath signal which primarily concentrates on the first Fresnel zone would have impacts on the detection capability of radar. According to the characteristics of the Fresnel zone, the Space Fresnel zone of electromagnetic wave transmission and the ground Fresnel zone under ultra-low altitude detection were defined. According to Huygens-Fresnel theorem, the mathematic models of the space and ground Fresnel zone. The influences of the distance between the feed source and receiving antenna and operating wavelength on the first dimensional Fresnel zone was analyzed by simulation. The change regulation of the first Fresnel zone along with complement angle of the radar seeker and distance between projection of radar seeker and target was obtained. The research results provided the theoretical foundation for multipath signal processing and finite truncation of reflector.

ultra-low altitude detection; space Fresnel zone; ground Fresnel zone

2016-03-01

国家自然科学基金(61372033)资助

邹高翔(1993-),男,湖南衡阳人,硕士研究生,研究方向:目标和环境复合散射特性以及快速计算方法。

TN011

A