鸭式布局制导火箭弹气动特性数值计算

陈永超,高欣宝,高 敏,张 磊

(解放军军械工程学院,石家庄 050003)

鸭式布局制导火箭弹气动特性数值计算

陈永超,高欣宝,高 敏,张 磊

(解放军军械工程学院,石家庄 050003)

为分析气动外形对鸭式布局制导火箭弹气动特性的影响,设计了两种具有不同尾翼的制导火箭弹模型,以三维Navier-Stokes方程为控制方程,采用结构网格、k-ε模型对制导火箭弹的绕流场进行了数值模拟,得到了两种结构方案下制导火箭弹的气动特性参数。研究结果表明,相较于6片尾翼设计方案,采用4片尾翼设计方案的制导火箭弹具有更大的升阻比,且静稳定性更好。

制导火箭弹;鸭式布局;气动特性;数值模拟

0 引言

海湾战争以来的局部战争表明,精确打击弹药在作战使用中占有的比例越来越高[1]。远程火箭弹具有射程远、威力大的优点,是我陆军装备的主要弹药之一。如何使其具有持续的弹道修正能力,从而实现精确打击是远程火箭弹的主要研究方向。其中主要的措施就是在弹体前部加装鸭舵,利用鸭舵偏转产生的控制力实现弹道修正,此外还需对尾翼进行设计,以便提高弹体的稳定性[2-3]。加装鸭舵和重新设计尾翼会改变全弹的阻力、升力、俯仰力矩及压心位置等气动特性,而这些气动特性会对制导火箭弹的射程及操控性产生影响,因此在结构设计之初须全面考虑,选出最合适的方案。

风洞试验是鸭式布局制导火箭弹气动特性分析的主要措施,但由于风洞试验成本高、实施难度大,故对所设计的每一种结构方案都进行风洞测试是不现实的。此外,计算流体力学(CFD)近几年发展迅速,已被广泛的用于计算各种制导弹药的气动特性,如炮射导弹气动特性的计算,二维弹道修正弹气动特性的计算等[4-5]。因此文中利用CFD方法,对鸭式布局制导火箭弹的扰流场进行数值模拟,从而获取鸭式布局制导火箭弹的气动特性随马赫数及攻角的变化规律,重点分析尾翼对鸭式布局制导火箭弹气动特性的影响,为鸭式布局制导火箭弹的结构设计提供依据。

1 计算方法及算法验证

1.1 数值计算方法

采用有限体积法对三维可压缩雷诺平均N-S方程进行离散,应用Gauss-Green公式,可以得到积分形式的守恒型N-S方程[6]:

式中:

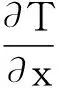
式中：ρ、V、E、p分别为密度、速度、单位质量总能和流体压力,τ为粘性应力张量。

湍流模型采用Realizable二方程k-ε模型,其最早由Launder和Spalding提出,具有较好的稳定性、经济性和比较高的计算精度,在湍流模型中应用最为广泛[7-8]。采用二阶迎风差分格式作为计算通量的方法,该方法保留了Taylor级数的第一项和第二项,可认为本地边界点的值等于上游网格控制点的值与一个增量的和。

1.2 计算区域和网格划分

将火箭弹外部流场作为计算域,为了准确的模拟火箭弹的飞行状态,同时缩短计算时间,所选取计算域应满足外边界处的空气不受火箭弹飞行的影响,且不宜取过大。在对某型122 mm鸭式布局制导火箭弹进行多次计算的过程中发现,计算域取直径50D(D为弹径),计算域入口距弹顶30D,计算域出口距弹底60D即可满足边界“无限远”要求。

所使用Realizablek-ε湍流模型对网格的质量要求较高,故采用全结构化网格,其对曲面的拟合采用参数化的方法得到,区域光滑,与弹体表面更贴近。此外,结构化网格存储简单,计算效率高,收敛性好。所划分计算域及纵向对称面内网格如图1所示。所生成弹体表面网格如图2所示。

由于计算域的边界不受火箭弹飞行的影响,故可设为压力远场边界条件。根据所研究火箭弹的实际飞行情况,计算条件分别选取了亚音速(Ma=0.8)和超音速(Ma=1.2)两个典型速度,攻角取0°～14°,暂不考虑舵偏角对气动特性的影响,故舵偏角取0°。弹体表面设置为粘性无滑移绝热固壁边界。

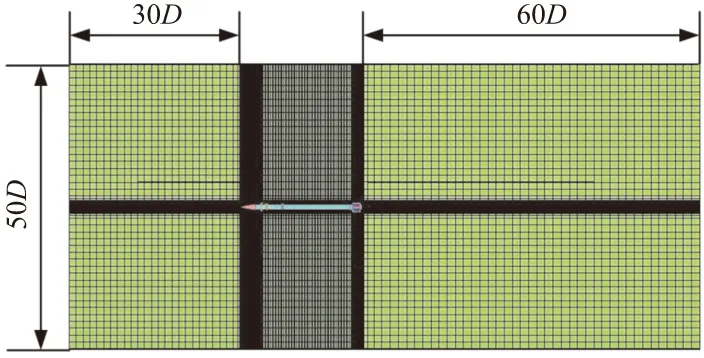
图1 计算域划分及对称面网格示意图

图2 鸭式布局制导火箭弹表面网格示意图

1.3 算法验证

为验证算法的有效性,对某型122 mm鸭式布局制导火箭弹进行了不同马赫数、不同攻角条件下的气动特性数值模拟。其中,将阻力系数、升力系数等部分数值模拟结果与实弹打靶数据进行了对比分析。图3给出了速度为1.2Ma时,不同攻角下阻力系数计算值与实验数据的比较。图4给出了速度为1.2Ma时,不同攻角下升力系数计算值与实验数据的比较。

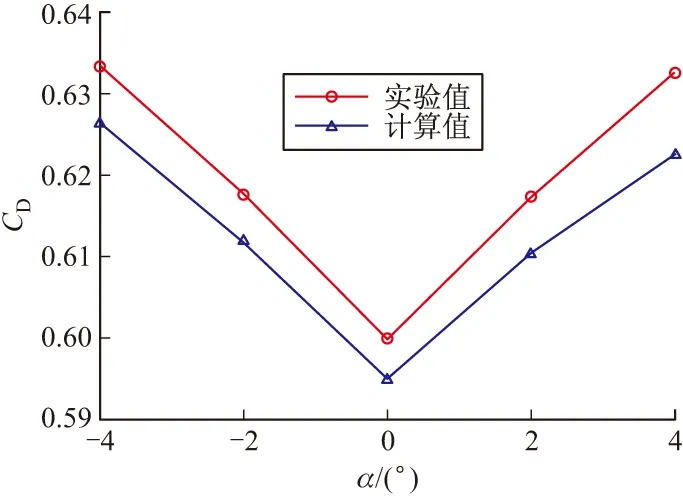
图3 阻力系数计算值与实验值的比较

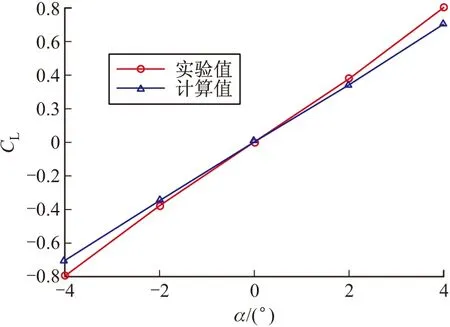
图4 升力系数计算值与实验值的比较

由图3、图4可见,数值计算结果和实验数据有很好的吻合度。因此,该计算方法可以作为具有相似结构布局的制导火箭弹气动特性数值研究的基础。

2 鸭式布局制导火箭弹结构方案设计

图5为所设计的两种鸭式布局制导火箭弹的结构示意图,其由某型远程火箭弹发展而来,主要特点为:鸭式气动布局,4片鸭舵,可折叠直尾翼。两种结构方案的主要区别为:方案一采用4片尾翼,方案二采用6片尾翼。

图5 鸭式布局制导火箭弹结构示意图

3 计算结果与分析

通过数值模拟得到了4片尾翼和6片尾翼两种结构方案下制导火箭弹的扰流场及气动特性。文中仅给出阻力系数、升力系数、俯仰力矩系数及压心系数的数值计算结果。

3.1 阻力系数

图6所示为马赫数分别为0.8和1.2时,两种结构方案下阻力系数随攻角的变化曲线。可以看出方案1和方案2的阻力系数随攻角的变化趋势基本一致。在亚音速时,方案2的阻力系数比方案1的阻力系数增加了约10%;在超音速时,方案2的阻力系数比方案1的阻力系数增加了约2%。

3.2 升力系数

图7所示为马赫数分别为0.8和1.2时,两种结构方案下升力系数随攻角的变化曲线。可以看出方案1和方案2的升力系数均随攻角的增加而增加,且增加的幅度逐渐增大。在攻角为14°时,亚音速情况下方案1的升力系数比方案2增加了约6%,超音速情况下方案1的升力系数比方案2增加了约15%。

3.3 俯仰力矩系数

图8所示为马赫数分别为0.8和1.2时,两种结构方案下俯仰力矩系数随攻角的变化曲线。可以看出俯仰力矩系数随攻角的变化规律与升力系数随攻角的变化规律类似,均随攻角的增大而增大,且增幅呈增大趋势。在攻角为14°时,亚音速情况下方案1的俯仰力矩系数比方案2增加了约25%,超音速情况下方案1的俯仰力矩系数比方案2增加了约42%。

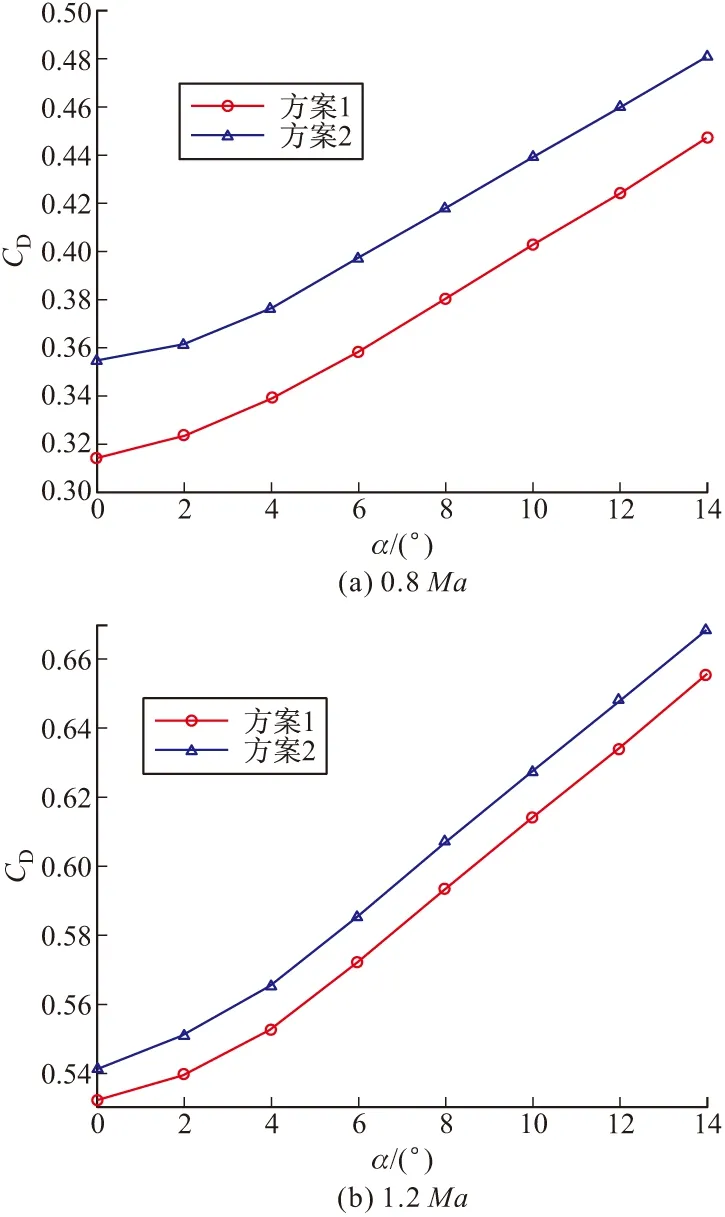
图6 两种结构方案下阻力系数随攻角的变化曲线

图7 两种结构方案下升力系数随攻角的变化曲线

3.4 压心系数

图9所示为马赫数分别为0.8和1.2时,两种结构方案下压心系数随攻角的变化曲线。可以看出随着攻角的增大,压心向后移动。在亚音速时,方案1的压心系数比方案2增加了约5%,在超音速时,方案1的压心系数比方案2增加了约8%。

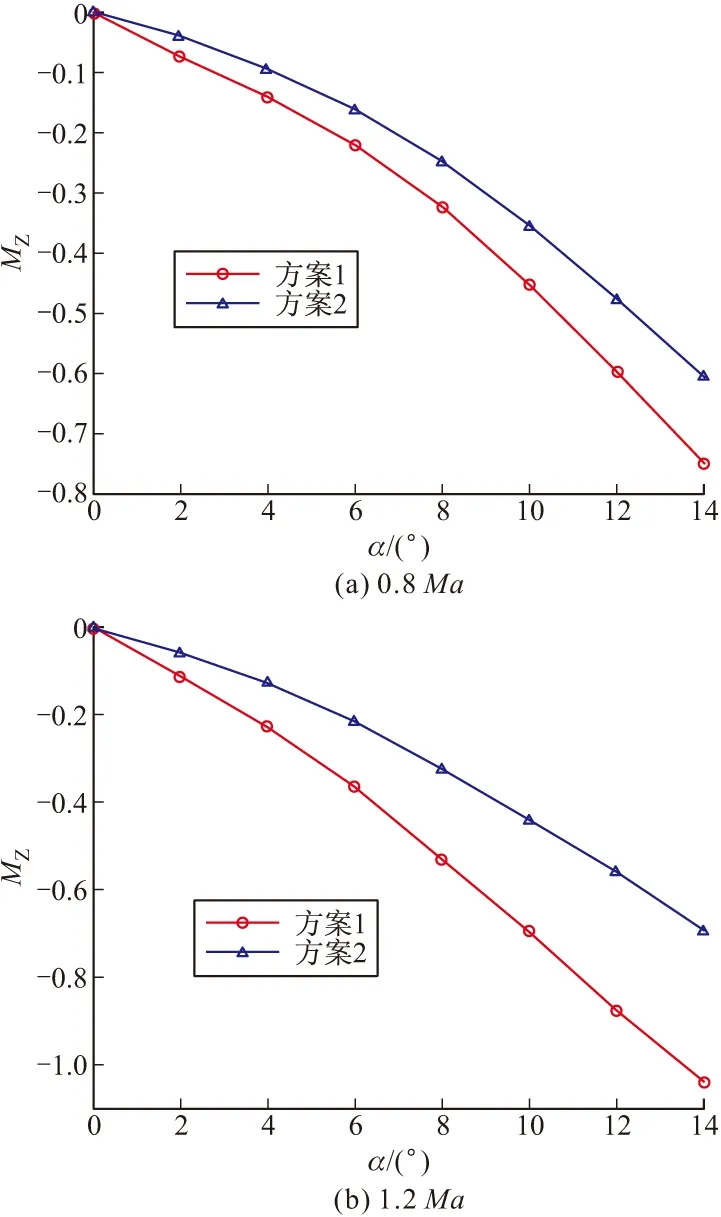
图8 两种结构方案下俯仰力距系数随攻角的变化曲线

图9 两种结构方案下压心系数随攻角的变化曲线

4 结论

利用经过算例验证的数值计算方法对所设计的鸭式布局制导火箭弹的绕流场进行了模拟,获得了4片尾翼和6片尾翼两种结构方案火箭弹的气动特性。研究结果表明,随着攻角的增大,阻力系数、升力系数、俯仰力矩系数均呈增大趋势,且随马赫数的增大这种现象更为明显;随着攻角的增大,压力中心后移,静稳定度增大;相较而言,4片尾翼的结构方案具有更大的升阻比,静稳定度更大,可作为首选方案,但还需要结合制导控制策略进行进一步的优化设计。

[1] 任武能, 史淑娟, 余达太. 从历次局部战争看美军精确制导弹药的发展 [J]. 导弹与航天运载技术, 2006(5): 58-61.

[2] 藏晓京, 朱爱平. 国外制导火箭弹发展概况 [J]. 飞航导弹, 2011(1): 13-17.

[3] 张民权, 刘东方, 王冬梅, 等. 弹道修正弹发展综述 [J]. 兵工学报, 2010, 31(2): 127-130.

[4] 郭庆阳, 姜毅, 郭利强, 等. 炮射导弹气动特性数值计算 [J]. 北京理工大学学报, 2011, 31(7): 772-775.

[5] 张嘉易, 王广, 郝永平. 二维弹道修正弹鸭舵修正机构气动特性研究 [J]. 弹箭与制导学报, 2013, 33(2): 88-92.

[6] 陆志良. 空气动力学 [M]. 北京: 北京航空航天大学出版社, 2009: 263-364.

[7] KUNZ R F, BOGER D A, STINEBRING D R, et al. A preconditioned navier-stokes method for two-phase flows with application to cavitation prediction: AIAA 99-3329[R]. 2000.

[8] LEROUX J B, COUTIER-DELGOSHA O, ASTO-LFI J A. A joint experimental and numerical study of mechanisms associated to instability of partial cavitation on two-dimensional hydrofoil [J]. Physics of Fluids, 2005, 17(5): 52-101.

Numerical Calculation of Aerodynamic Characteristic of Canard Configuration Guided Rocket

CHEN Yongchao,GAO Xinbao,GAO Min,ZHANG Lei

(Ordnance Engineering College of PLA, Shijiazhuang 050003, China)

Two kinds of guided rocket model with different fins were designed to analyse the effect of aerodynamic configuration on aerodynamic characteristic of canard configuration guided rocket. Using 3D Navier-Stokes equation as governing equation, using structured grid, k-ε model was used to simulate the flow field of guided rocket, and the aerodynamic characteristic parameters of two diferent structures were obtained. The results proved that the configuration with four fins had lager lift-drag ratio and better static stability compared with the configuration with six fins.

guided rocket; canard configuration; aerodynamic characteristics; numerical simulation

2016-03-11

装备预研基金资助

陈永超(1989-),男,河南平顶山人,博士研究生,研究方向:弹药系统设计与试验评估。

V211

A